10.4 平移 学习任务单 2023-2024学年沪科版数学七年级下册(含答案)
文档属性
| 名称 | 10.4 平移 学习任务单 2023-2024学年沪科版数学七年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 09:13:10 | ||
图片预览


文档简介
10.4 平移
素养目标
1.通过具体实例认识平移,知道平移的相关概念.
2.掌握平移的性质,能从复杂的平移图形中识别基本图形.
3.能按要求作出简单图形平移后的图形,能用平移变换进行简单的图案设计.
◎重点:平移的基本性质.
预习导学
知识点一 平移的概念
阅读教材中的相关内容,回答下列问题:
1.(1)观察:图中一艘小船从右边缓缓向左边开动,开动了 个格子.
(2)思考:图形上的点B移动到了点A,向 边,移动了 个格子,那么点D呢 点E呢 点F呢
2.揭示概念:(1)像上面那样,一个图形沿着某个方向移动一定距离,这种图形的变换叫做 .
(2)图形上每一点都沿着同一方向移动 的距离.(填“相同”或“不同”)
3.明晰概念:平移前的图形与平移后的图形是相互对应的,点B与点A称为 点;线段AC与线段BD称为 线段.
4.讨论:平移的两个要素是什么
【答案】1.(1)11 (2)左 11 同样向左边移动了11个格子
2.(1)平移 (2)相同
3.对应 对应
4.平移的方向和平移的距离.
知识点二 平移的性质
阅读教材中的相关内容,回答下列问题:
1.(1)操作:已知△ABC,用硬纸片制作△ABC,借助直尺将硬纸片△ABC沿AD方向平移,使点A落在点D.画一画平移后点B的对应点和点C的对应点.(可用一块三角板沿线段平移代替)
(2)观察并思考:①对应点的连线AD、BE、CF之间的位置和大小有什么关系 可以用直尺量一量,比一比.
②平移前的△ABC与平移后的△DEF的大小和形状有什么关系
2.讨论:平移前后两个图形中的对应线段和对应角有什么关系
【答案】1.(1)
(2)①平行且相等 ②大小相等,形状不变.
2.对应线段平行(或在同一条直线上)且相等,对应角相等.
【归纳总结】平移的性质:(1)一个图形和它经过平移后所得的图形中,连接各组对应点的线段互相 (或在 )且 ;(2)平移只改变图形的位置,不改变图形的 和 .
【答案】(1)平行 同一条直线上 相等 (2)形状 大小
对点自测
1.在下列现象中,属于平移的是 ( )
A.月亮绕地球运动
B.翻开书中的每一页纸张
C.教室可移动黑板的左右移动
D.投掷出去的铅球
2.关于图形平移的特征叙述,有下列两种说法:①一个图形和它经过平移所得的图形中,两组对应点的连线一定平行;②一个图形和它经过平移所得的图形中,两组对应点的连线一定相等.其中判断正确的是 ( )
A.①错②对 B.①对②错
C.①②都错 D.①②都对
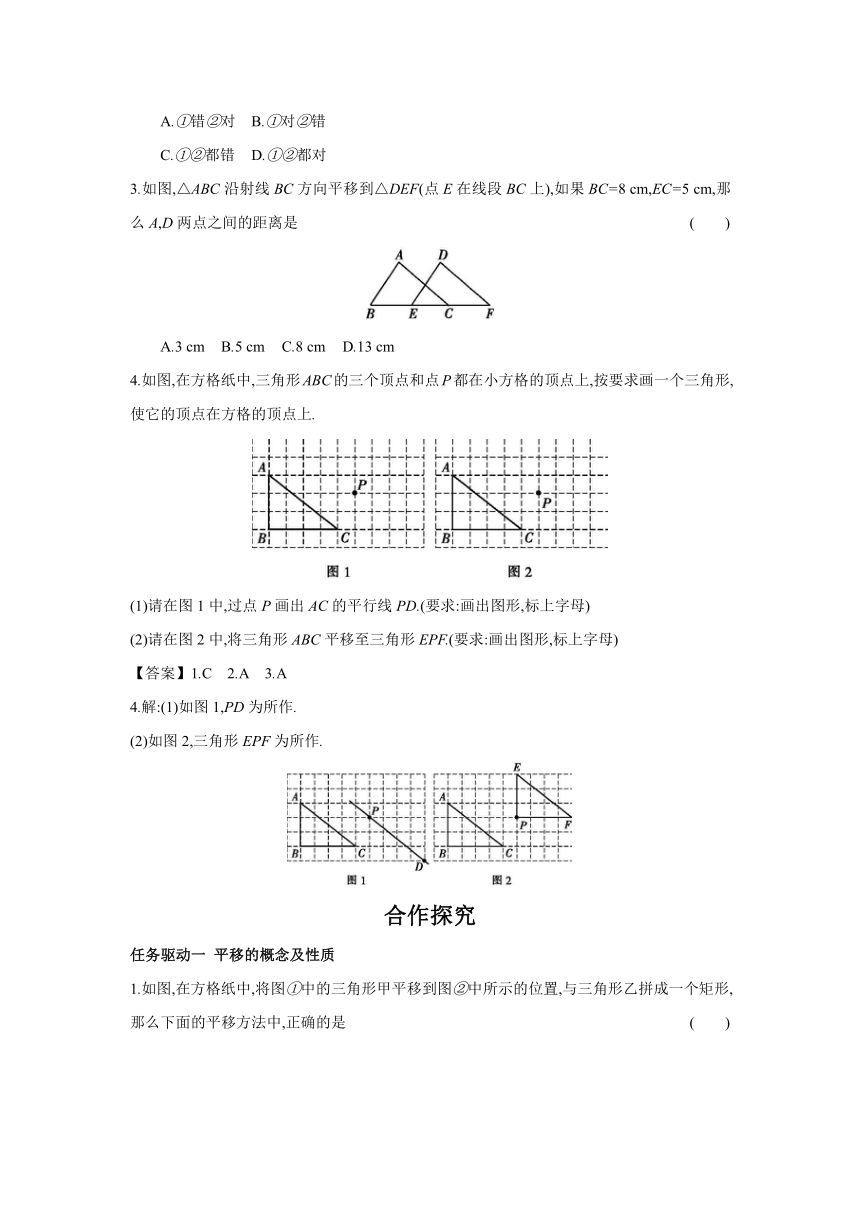
3.如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上),如果BC=8 cm,EC=5 cm,那么A,D两点之间的距离是 ( )
A.3 cm B.5 cm C.8 cm D.13 cm
4.如图,在方格纸中,三角形ABC的三个顶点和点P都在小方格的顶点上,按要求画一个三角形,使它的顶点在方格的顶点上.
(1)请在图1中,过点P画出AC的平行线PD.(要求:画出图形,标上字母)
(2)请在图2中,将三角形ABC平移至三角形EPF.(要求:画出图形,标上字母)
【答案】1.C 2.A 3.A
4.解:(1)如图1,PD为所作.
(2)如图2,三角形EPF为所作.
合作探究
任务驱动一 平移的概念及性质
1.如图,在方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么下面的平移方法中,正确的是 ( )
A.先向下平移3格,再向右平移1格
B.先向下平移2格,再向右平移1格
C.先向下平移2格,再向右平移2格
D.先向下平移3格,再向右平移2格
2.如图,这是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米.为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为 ( )
A.100米 B.99米
C.98米 D.74米
【答案】1.D 2.C
[变式训练]某会展中心重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价100元,主楼梯道宽2 m,其侧面如图所示,则购买地毯至少需要 元.
【答案】1680
任务驱动二 平移与作图
3.如图,将图中的三角形向右平移8格,梯形向上平移4格能够得到什么图案
【答案】3.解:如图,把三角形三个顶点分别向右平移8格,得到三个对应点,分别连接各点,得到平移后的三角形.用同样的方法将梯形的四个顶点分别向上平移4格并连接,得到平移后的梯形,最后可得到一条小船的图案.
[变式训练]如图,经过平移,小船上的点A移动到了点B的位置,试作出平移后的小船.
【答案】解:如图所示.
【方法归纳交流】作平移后的图形首先找到图形的 ,通过对应点确定平移的 ,由平移的性质作出其他关键点的对应点,再分别连接各对应点即可.
【答案】一对对应点 距离和方向
素养小测
1.如图,平移三角形ABC得到三角形DEF,其中点A的对应点是点D,则下列结论中错误的是 ( )
A.AD∥BE B.∠BAC=∠DFE
C.AC=DF D.∠ABC=∠DEF
2.如图,将三角形ABC沿BC方向向右平移3 cm得到三角形DEF,若三角形ABC的周长为20 cm,则四边形ABFD的周长为 ( )
A.23 cm B.26 cm
C.29 cm D.32 cm
3.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3= °.
4.将图中的四边形按箭头方向平移2 cm.
5.如图,长方形ABCD的长BC为5,宽AB为4,若将其沿着射线BC方向平移到长方形EFGH处,则长方形CDEF的周长是长方形ABCD周长为,求出长方形ABCD平移的距离.
【答案】1.B 2.B 3.110
4.解:
5.解:设长方形ABCD平移距离AE=x.
因为长方形ABCD的长为5,宽为4,所以长方形ABCD的周长=18.
因为长方形CDEF的周长是长方形ABCD周长为,
所以4+4+5-x+5-x=18×,
所以x=3,即长方形ABCD平移的距离为3.
素养目标
1.通过具体实例认识平移,知道平移的相关概念.
2.掌握平移的性质,能从复杂的平移图形中识别基本图形.
3.能按要求作出简单图形平移后的图形,能用平移变换进行简单的图案设计.
◎重点:平移的基本性质.
预习导学
知识点一 平移的概念
阅读教材中的相关内容,回答下列问题:
1.(1)观察:图中一艘小船从右边缓缓向左边开动,开动了 个格子.
(2)思考:图形上的点B移动到了点A,向 边,移动了 个格子,那么点D呢 点E呢 点F呢
2.揭示概念:(1)像上面那样,一个图形沿着某个方向移动一定距离,这种图形的变换叫做 .
(2)图形上每一点都沿着同一方向移动 的距离.(填“相同”或“不同”)
3.明晰概念:平移前的图形与平移后的图形是相互对应的,点B与点A称为 点;线段AC与线段BD称为 线段.
4.讨论:平移的两个要素是什么
【答案】1.(1)11 (2)左 11 同样向左边移动了11个格子
2.(1)平移 (2)相同
3.对应 对应
4.平移的方向和平移的距离.
知识点二 平移的性质
阅读教材中的相关内容,回答下列问题:
1.(1)操作:已知△ABC,用硬纸片制作△ABC,借助直尺将硬纸片△ABC沿AD方向平移,使点A落在点D.画一画平移后点B的对应点和点C的对应点.(可用一块三角板沿线段平移代替)
(2)观察并思考:①对应点的连线AD、BE、CF之间的位置和大小有什么关系 可以用直尺量一量,比一比.
②平移前的△ABC与平移后的△DEF的大小和形状有什么关系
2.讨论:平移前后两个图形中的对应线段和对应角有什么关系
【答案】1.(1)
(2)①平行且相等 ②大小相等,形状不变.
2.对应线段平行(或在同一条直线上)且相等,对应角相等.
【归纳总结】平移的性质:(1)一个图形和它经过平移后所得的图形中,连接各组对应点的线段互相 (或在 )且 ;(2)平移只改变图形的位置,不改变图形的 和 .
【答案】(1)平行 同一条直线上 相等 (2)形状 大小
对点自测
1.在下列现象中,属于平移的是 ( )
A.月亮绕地球运动
B.翻开书中的每一页纸张
C.教室可移动黑板的左右移动
D.投掷出去的铅球
2.关于图形平移的特征叙述,有下列两种说法:①一个图形和它经过平移所得的图形中,两组对应点的连线一定平行;②一个图形和它经过平移所得的图形中,两组对应点的连线一定相等.其中判断正确的是 ( )
A.①错②对 B.①对②错
C.①②都错 D.①②都对
3.如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上),如果BC=8 cm,EC=5 cm,那么A,D两点之间的距离是 ( )
A.3 cm B.5 cm C.8 cm D.13 cm
4.如图,在方格纸中,三角形ABC的三个顶点和点P都在小方格的顶点上,按要求画一个三角形,使它的顶点在方格的顶点上.
(1)请在图1中,过点P画出AC的平行线PD.(要求:画出图形,标上字母)
(2)请在图2中,将三角形ABC平移至三角形EPF.(要求:画出图形,标上字母)
【答案】1.C 2.A 3.A
4.解:(1)如图1,PD为所作.
(2)如图2,三角形EPF为所作.
合作探究
任务驱动一 平移的概念及性质
1.如图,在方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么下面的平移方法中,正确的是 ( )
A.先向下平移3格,再向右平移1格
B.先向下平移2格,再向右平移1格
C.先向下平移2格,再向右平移2格
D.先向下平移3格,再向右平移2格
2.如图,这是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米.为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为 ( )
A.100米 B.99米
C.98米 D.74米
【答案】1.D 2.C
[变式训练]某会展中心重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价100元,主楼梯道宽2 m,其侧面如图所示,则购买地毯至少需要 元.
【答案】1680
任务驱动二 平移与作图
3.如图,将图中的三角形向右平移8格,梯形向上平移4格能够得到什么图案
【答案】3.解:如图,把三角形三个顶点分别向右平移8格,得到三个对应点,分别连接各点,得到平移后的三角形.用同样的方法将梯形的四个顶点分别向上平移4格并连接,得到平移后的梯形,最后可得到一条小船的图案.
[变式训练]如图,经过平移,小船上的点A移动到了点B的位置,试作出平移后的小船.
【答案】解:如图所示.
【方法归纳交流】作平移后的图形首先找到图形的 ,通过对应点确定平移的 ,由平移的性质作出其他关键点的对应点,再分别连接各对应点即可.
【答案】一对对应点 距离和方向
素养小测
1.如图,平移三角形ABC得到三角形DEF,其中点A的对应点是点D,则下列结论中错误的是 ( )
A.AD∥BE B.∠BAC=∠DFE
C.AC=DF D.∠ABC=∠DEF
2.如图,将三角形ABC沿BC方向向右平移3 cm得到三角形DEF,若三角形ABC的周长为20 cm,则四边形ABFD的周长为 ( )
A.23 cm B.26 cm
C.29 cm D.32 cm
3.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3= °.
4.将图中的四边形按箭头方向平移2 cm.
5.如图,长方形ABCD的长BC为5,宽AB为4,若将其沿着射线BC方向平移到长方形EFGH处,则长方形CDEF的周长是长方形ABCD周长为,求出长方形ABCD平移的距离.
【答案】1.B 2.B 3.110
4.解:
5.解:设长方形ABCD平移距离AE=x.
因为长方形ABCD的长为5,宽为4,所以长方形ABCD的周长=18.
因为长方形CDEF的周长是长方形ABCD周长为,
所以4+4+5-x+5-x=18×,
所以x=3,即长方形ABCD平移的距离为3.
