10.2 第2课时 同位角相等,两直线平行 学习任务单 2023-2024学年沪科版数学七年级下册(含答案)
文档属性
| 名称 | 10.2 第2课时 同位角相等,两直线平行 学习任务单 2023-2024学年沪科版数学七年级下册(含答案) | 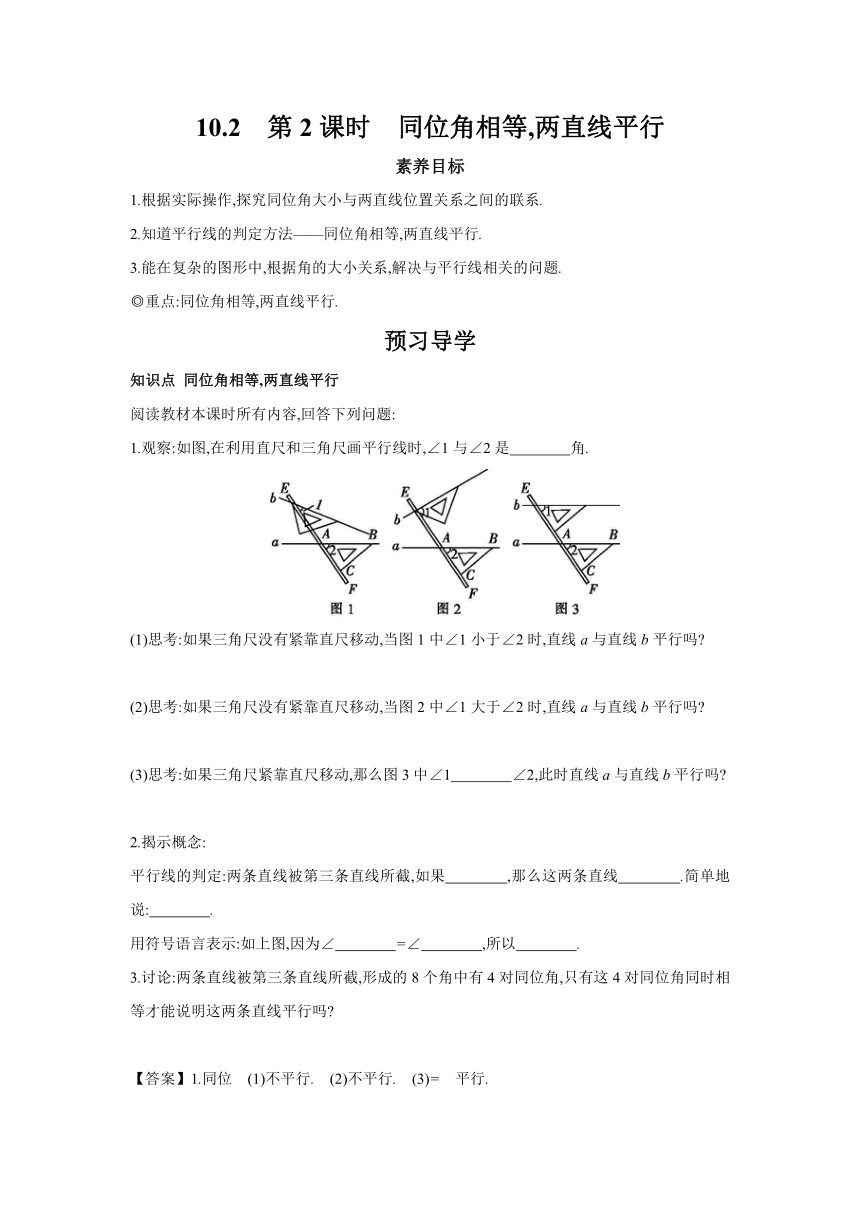 | |
| 格式 | docx | ||
| 文件大小 | 109.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 14:57:32 | ||
图片预览

文档简介
10.2 第2课时 同位角相等,两直线平行
素养目标
1.根据实际操作,探究同位角大小与两直线位置关系之间的联系.
2.知道平行线的判定方法——同位角相等,两直线平行.
3.能在复杂的图形中,根据角的大小关系,解决与平行线相关的问题.
◎重点:同位角相等,两直线平行.
预习导学
知识点 同位角相等,两直线平行
阅读教材本课时所有内容,回答下列问题:
1.观察:如图,在利用直尺和三角尺画平行线时,∠1与∠2是 角.
(1)思考:如果三角尺没有紧靠直尺移动,当图1中∠1小于∠2时,直线a与直线b平行吗
(2)思考:如果三角尺没有紧靠直尺移动,当图2中∠1大于∠2时,直线a与直线b平行吗
(3)思考:如果三角尺紧靠直尺移动,那么图3中∠1 ∠2,此时直线a与直线b平行吗
2.揭示概念:
平行线的判定:两条直线被第三条直线所截,如果 ,那么这两条直线 .简单地说: .
用符号语言表示:如上图,因为∠ =∠ ,所以 .
3.讨论:两条直线被第三条直线所截,形成的8个角中有4对同位角,只有这4对同位角同时相等才能说明这两条直线平行吗
【答案】1.同位 (1)不平行. (2)不平行. (3)= 平行.
2.同位角相等 平行 同位角相等,两直线平行 1 2 a∥b
3.不是,只要其中一对同位角相等,就可以说明这两条直线平行.
对点自测
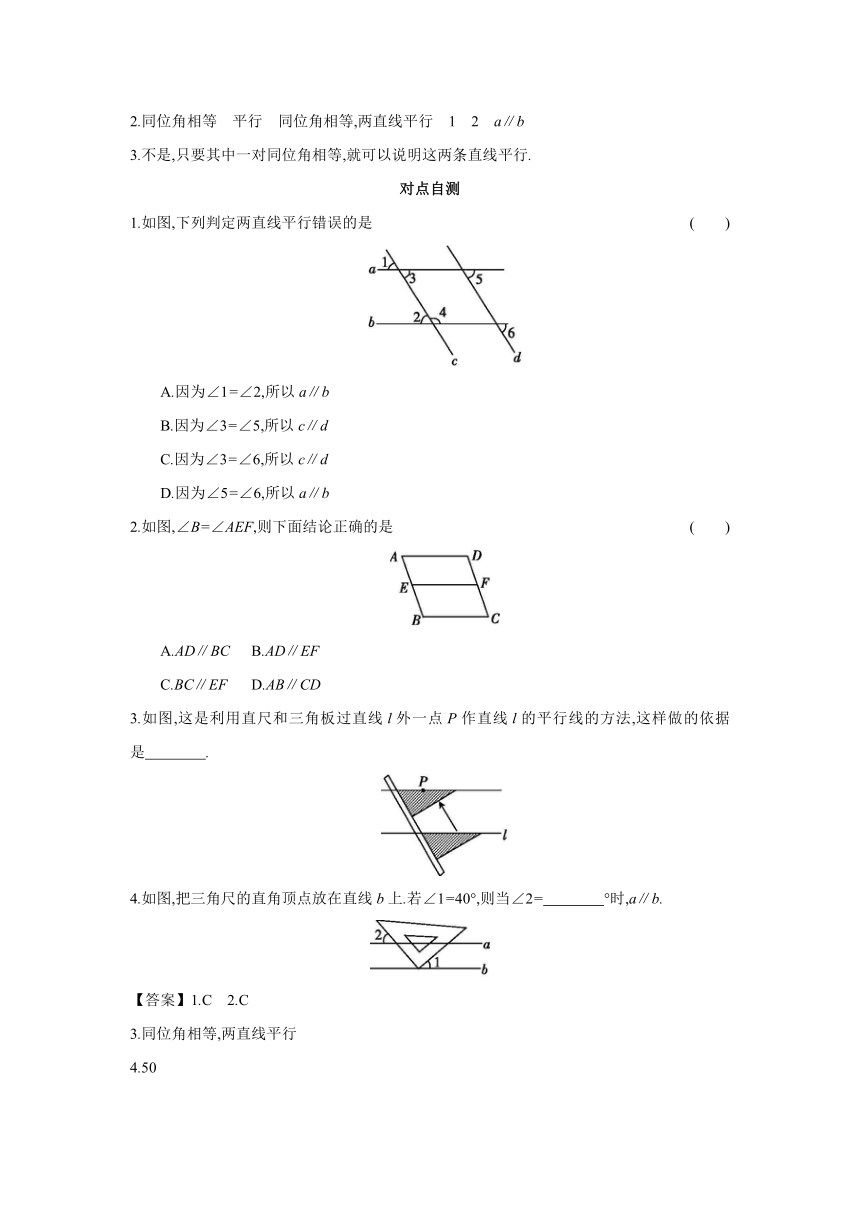
1.如图,下列判定两直线平行错误的是 ( )
A.因为∠1=∠2,所以a∥b
B.因为∠3=∠5,所以c∥d
C.因为∠3=∠6,所以c∥d
D.因为∠5=∠6,所以a∥b
2.如图,∠B=∠AEF,则下面结论正确的是 ( )
A.AD∥BC B.AD∥EF
C.BC∥EF D.AB∥CD
3.如图,这是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
4.如图,把三角尺的直角顶点放在直线b上.若∠1=40°,则当∠2= °时,a∥b.
【答案】1.C 2.C
3.同位角相等,两直线平行
4.50
合作探究
任务驱动 同位角相等,两直线平行
1.如图,∠A=70°,A、B、E三点在同一条直线上,且∠CBE=70°,那么直线 ∥ ,根据 .
2.如图,∠1=120°,∠2=60°,试说明AB∥CD.
【答案】1.AD BC 同位角相等,两直线平行
2.解:因为∠1+∠3=180°,∠1=120°,
所以∠3=60°.
又∠2=60°,所以∠3=∠2,
所以AB∥CD(同位角相等,两直线平行).
【方法归纳交流】根据 ,可通过证明 或 证明AB∥CD.
【答案】同位角相等,两直线平行 ∠1=∠4 ∠2=∠3
3.如图,根据下列条件可以判断哪两条直线平行 并说明判断的依据是什么.
(1)∠A=∠1;(2)∠1=∠D.
【答案】3.(1)解:(1)由∠A=∠1,可得AB∥DE,依据是同位角相等,两直线平行.
(2)由∠1=∠D,可得AC∥DF,依据是同位角相等,两直线平行.
素养小测
1.如图,以下条件能判定直线a,b互相平行的有 ( )
①∠1=∠2;②∠3=∠4;③∠3=∠6;④∠5+∠6=180°.
A.1个 B.2个 C.3个 D.4个
2.如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2.
(1)求证:AB∥CD.
(2)试判断BM与DN是否平行 为什么
【答案】1.D
2.解:(1)证明:因为AB⊥EF于点B,CD⊥EF于点D,
所以∠ABE=∠CDE=90°,所以AB∥CD.
(2)BM∥DN.理由:
因为AB⊥EF于点B,CD⊥EF于点D,
所以∠ABE=∠CDE=90°.
因为∠1=∠2,所以∠ABE-∠1=∠CDE-∠2,即∠MBE=∠NDE,
所以BM∥DN.
素养目标
1.根据实际操作,探究同位角大小与两直线位置关系之间的联系.
2.知道平行线的判定方法——同位角相等,两直线平行.
3.能在复杂的图形中,根据角的大小关系,解决与平行线相关的问题.
◎重点:同位角相等,两直线平行.
预习导学
知识点 同位角相等,两直线平行
阅读教材本课时所有内容,回答下列问题:
1.观察:如图,在利用直尺和三角尺画平行线时,∠1与∠2是 角.
(1)思考:如果三角尺没有紧靠直尺移动,当图1中∠1小于∠2时,直线a与直线b平行吗
(2)思考:如果三角尺没有紧靠直尺移动,当图2中∠1大于∠2时,直线a与直线b平行吗
(3)思考:如果三角尺紧靠直尺移动,那么图3中∠1 ∠2,此时直线a与直线b平行吗
2.揭示概念:
平行线的判定:两条直线被第三条直线所截,如果 ,那么这两条直线 .简单地说: .
用符号语言表示:如上图,因为∠ =∠ ,所以 .
3.讨论:两条直线被第三条直线所截,形成的8个角中有4对同位角,只有这4对同位角同时相等才能说明这两条直线平行吗
【答案】1.同位 (1)不平行. (2)不平行. (3)= 平行.
2.同位角相等 平行 同位角相等,两直线平行 1 2 a∥b
3.不是,只要其中一对同位角相等,就可以说明这两条直线平行.
对点自测
1.如图,下列判定两直线平行错误的是 ( )
A.因为∠1=∠2,所以a∥b
B.因为∠3=∠5,所以c∥d
C.因为∠3=∠6,所以c∥d
D.因为∠5=∠6,所以a∥b
2.如图,∠B=∠AEF,则下面结论正确的是 ( )
A.AD∥BC B.AD∥EF
C.BC∥EF D.AB∥CD
3.如图,这是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
4.如图,把三角尺的直角顶点放在直线b上.若∠1=40°,则当∠2= °时,a∥b.
【答案】1.C 2.C
3.同位角相等,两直线平行
4.50
合作探究
任务驱动 同位角相等,两直线平行
1.如图,∠A=70°,A、B、E三点在同一条直线上,且∠CBE=70°,那么直线 ∥ ,根据 .
2.如图,∠1=120°,∠2=60°,试说明AB∥CD.
【答案】1.AD BC 同位角相等,两直线平行
2.解:因为∠1+∠3=180°,∠1=120°,
所以∠3=60°.
又∠2=60°,所以∠3=∠2,
所以AB∥CD(同位角相等,两直线平行).
【方法归纳交流】根据 ,可通过证明 或 证明AB∥CD.
【答案】同位角相等,两直线平行 ∠1=∠4 ∠2=∠3
3.如图,根据下列条件可以判断哪两条直线平行 并说明判断的依据是什么.
(1)∠A=∠1;(2)∠1=∠D.
【答案】3.(1)解:(1)由∠A=∠1,可得AB∥DE,依据是同位角相等,两直线平行.
(2)由∠1=∠D,可得AC∥DF,依据是同位角相等,两直线平行.
素养小测
1.如图,以下条件能判定直线a,b互相平行的有 ( )
①∠1=∠2;②∠3=∠4;③∠3=∠6;④∠5+∠6=180°.
A.1个 B.2个 C.3个 D.4个
2.如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2.
(1)求证:AB∥CD.
(2)试判断BM与DN是否平行 为什么
【答案】1.D
2.解:(1)证明:因为AB⊥EF于点B,CD⊥EF于点D,
所以∠ABE=∠CDE=90°,所以AB∥CD.
(2)BM∥DN.理由:
因为AB⊥EF于点B,CD⊥EF于点D,
所以∠ABE=∠CDE=90°.
因为∠1=∠2,所以∠ABE-∠1=∠CDE-∠2,即∠MBE=∠NDE,
所以BM∥DN.
