24.4.2 直线与圆的位置关系 导学案 2023--2024学年沪科版九年级数学下册(无答案)
文档属性
| 名称 | 24.4.2 直线与圆的位置关系 导学案 2023--2024学年沪科版九年级数学下册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 116.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 23:19:10 | ||
图片预览

文档简介
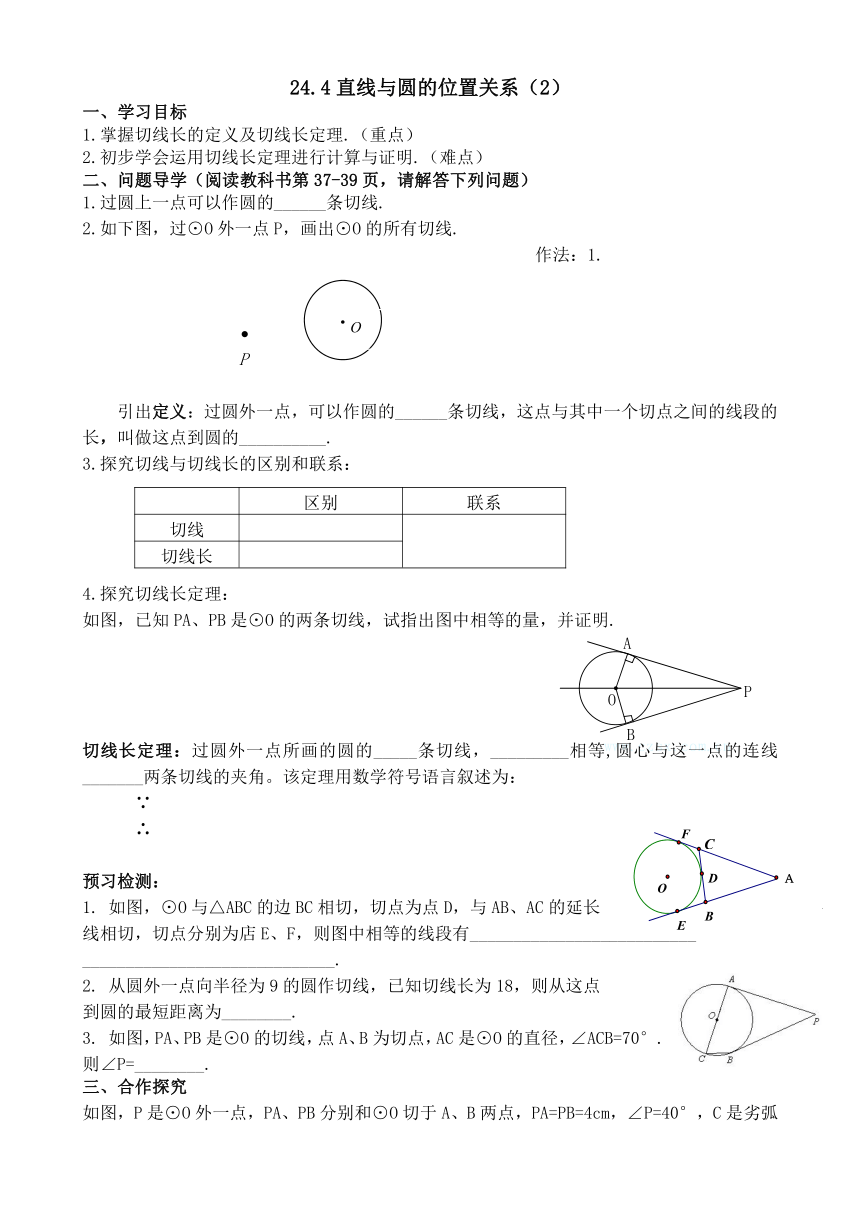
24.4直线与圆的位置关系(2)
学习目标
1.掌握切线长的定义及切线长定理.(重点)
2.初步学会运用切线长定理进行计算与证明.(难点)
二、问题导学(阅读教科书第37-39页,请解答下列问题)
1.过圆上一点可以作圆的______条切线.
2.如下图,过⊙O外一点P,画出⊙O的所有切线.
作法:1.
(
·
O
)
P
引出定义:过圆外一点,可以作圆的______条切线,这点与其中一个切点之间的线段的长,叫做这点到圆的__________.
3.探究切线与切线长的区别和联系:
区别 联系
切线
切线长
4.探究切线长定理:
如图,已知PA、PB是⊙O的两条切线,试指出图中相等的量,并证明.
切线长定理:过圆外一点所画的圆的_____条切线,_________相等,圆心与这一点的连线_______两条切线的夹角。该定理用数学符号语言叙述为:
∵
(
E
D
F
C
B
O
A
)∴
预习检测:
(
A
)如图,⊙O与△ABC的边BC相切,切点为点D,与AB、AC的延长
线相切,切点分别为店E、F,则图中相等的线段有__________________________
_____________________________.
从圆外一点向半径为9的圆作切线,已知切线长为18,则从这点
到圆的最短距离为________.
3. 如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=70°.则∠P=________.
三、合作探究
如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B两点,PA=PB=4cm,∠P=40°,C是劣弧AB上任意一点,过点C作⊙O的切线,分别交PA、PB与点D、E,试求:
(1)△PDE的周长;
(2)∠DOE的度数.
四、能力提升
如图①,已知AB为☉O的直径,∠A=∠B=90°,DE与☉O相切于点E,☉O的半径为,AD=2.
(1)求BC的长;
(2)如图②,连接AE并延长交BC的延长线于点G,求EG的长.
五、课堂小结
六、当堂检测
1.如图,PA切☉O于点A,PB切☉O于点B,连接OP.若∠APO=30°,OA=2,则PB的长为
2.如图,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,则下列结论中错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.∠PAB=2∠1
第1题图 第2题图 第3题图 第4题图
3.如图,从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B.若∠APB=60°,弦AB=4,则PA= .
4. 如图,P为⊙O外一点,PA、PB是⊙O的两条切线,A、B是切点,BC是直径.
(1)求证:AC∥OP
︵
(2)如果∠APC=70°,求 AC的度数
学习目标
1.掌握切线长的定义及切线长定理.(重点)
2.初步学会运用切线长定理进行计算与证明.(难点)
二、问题导学(阅读教科书第37-39页,请解答下列问题)
1.过圆上一点可以作圆的______条切线.
2.如下图,过⊙O外一点P,画出⊙O的所有切线.
作法:1.
(
·
O
)
P
引出定义:过圆外一点,可以作圆的______条切线,这点与其中一个切点之间的线段的长,叫做这点到圆的__________.
3.探究切线与切线长的区别和联系:
区别 联系
切线
切线长
4.探究切线长定理:
如图,已知PA、PB是⊙O的两条切线,试指出图中相等的量,并证明.
切线长定理:过圆外一点所画的圆的_____条切线,_________相等,圆心与这一点的连线_______两条切线的夹角。该定理用数学符号语言叙述为:
∵
(
E
D
F
C
B
O
A
)∴
预习检测:
(
A
)如图,⊙O与△ABC的边BC相切,切点为点D,与AB、AC的延长
线相切,切点分别为店E、F,则图中相等的线段有__________________________
_____________________________.
从圆外一点向半径为9的圆作切线,已知切线长为18,则从这点
到圆的最短距离为________.
3. 如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=70°.则∠P=________.
三、合作探究
如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B两点,PA=PB=4cm,∠P=40°,C是劣弧AB上任意一点,过点C作⊙O的切线,分别交PA、PB与点D、E,试求:
(1)△PDE的周长;
(2)∠DOE的度数.
四、能力提升
如图①,已知AB为☉O的直径,∠A=∠B=90°,DE与☉O相切于点E,☉O的半径为,AD=2.
(1)求BC的长;
(2)如图②,连接AE并延长交BC的延长线于点G,求EG的长.
五、课堂小结
六、当堂检测
1.如图,PA切☉O于点A,PB切☉O于点B,连接OP.若∠APO=30°,OA=2,则PB的长为
2.如图,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,则下列结论中错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.∠PAB=2∠1
第1题图 第2题图 第3题图 第4题图
3.如图,从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B.若∠APB=60°,弦AB=4,则PA= .
4. 如图,P为⊙O外一点,PA、PB是⊙O的两条切线,A、B是切点,BC是直径.
(1)求证:AC∥OP
︵
(2)如果∠APC=70°,求 AC的度数
