24.3.1圆周角 导学案 2023--2024学年沪科版九年级数学下册(无答案)
文档属性
| 名称 | 24.3.1圆周角 导学案 2023--2024学年沪科版九年级数学下册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 648.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 08:50:24 | ||
图片预览

文档简介
24.3 圆周角(1)
学习目标
1.理解圆周角的定义,了解与圆心角的关系,会在具体情景中辨别圆周角.
2.掌握圆周角定理及推论,并会运用这些知识进行简单的计算和证明.
二、问题导学(阅读教科书第 27-28页,请解答下列问题)
1.什么是圆心角?
(
A
B
C
O
)
2.圆心角的度数与它所对弧的度数是什么关系?
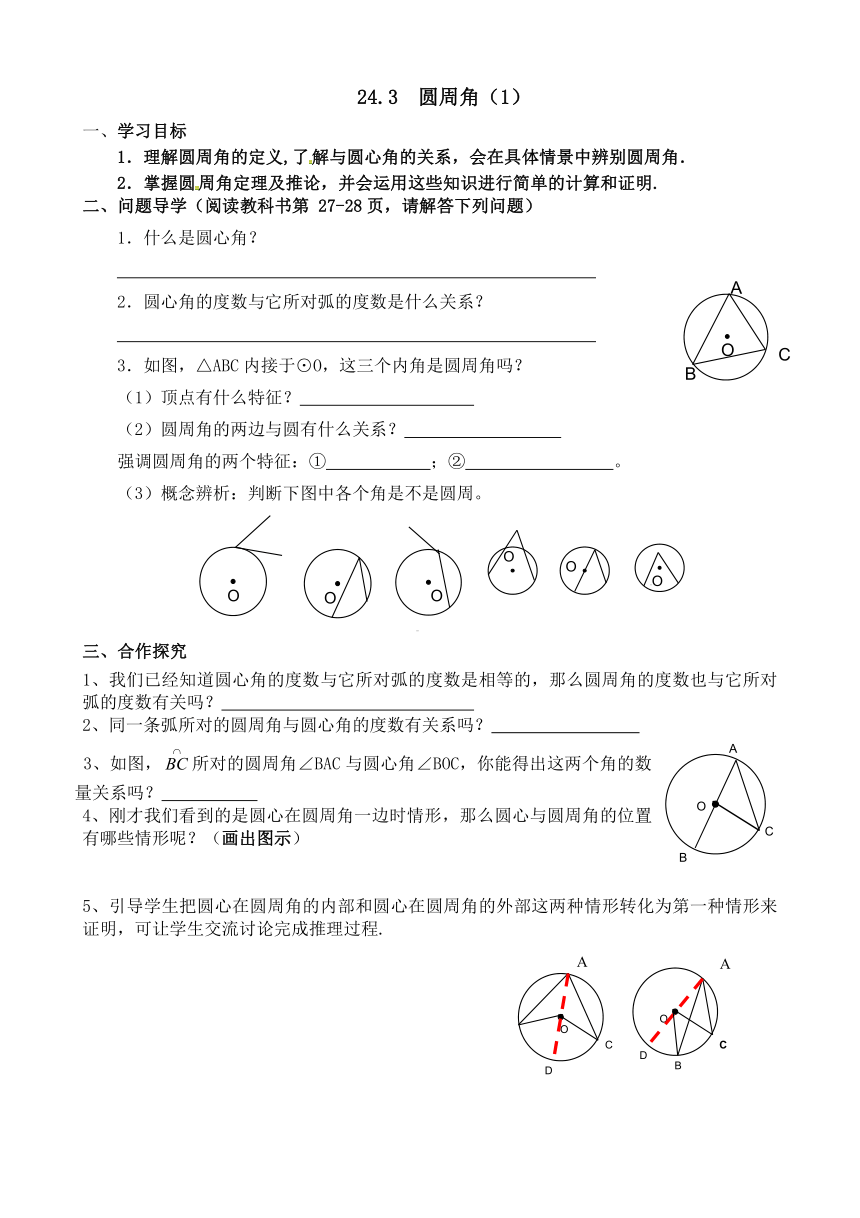
3.如图,△ABC内接于⊙O,这三个内角是圆周角吗?
(1)顶点有什么特征?
圆周角的两边与圆有什么关系?
强调圆周角的两个特征:① ;② 。
(3)概念辨析:判断下图中各个角是不是圆周。
(
O
) (
:
O
O
O
) (
O
) (
O
)
三、合作探究
1、我们已经知道圆心角的度数与它所对弧的度数是相等的,那么圆周角的度数也与它所对弧的度数有关吗?
(
C
A
O
B
)2、同一条弧所对的圆周角与圆心角的度数有关系吗?
3、如图,所对的圆周角∠BAC与圆心角∠BOC,你能得出这两个角的数量关系吗?
4、刚才我们看到的是圆心在圆周角一边时情形,那么圆心与圆周角的位置有哪些情形呢?(画出图示)
5、引导学生把圆心在圆周角的内部和圆心在圆周角的外部这两种情形转化为第一种情形来证明,可让学生交流讨论完成推理过程.
(
A
) (
A
) (
C
C
O
D
O
B
D
)
圆周角定理: .
圆周角的度数 = 同弧所对圆心角的度数的_ ___
推论 1:
推论 2:
能力提升
已知:如图,AB是⊙O的直径,弦CD⊥AB于E,∠ACD=30°,AE=2cm.求DB长.
课堂小结
六、当堂检测
1.如图1,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A.35° B.45° C.55° D.65°
2.如图2所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的度数
是( )
A.80° B.120° C.100 D.90°
3.如图3,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.
若∠BDC=40°,则∠AMB的度数不可能是( )
A.45° B.60° C.75° D.85°
4.在半径为1的⊙O中,弦AB、AC的长分别为和,求∠BAC的度数.
学习目标
1.理解圆周角的定义,了解与圆心角的关系,会在具体情景中辨别圆周角.
2.掌握圆周角定理及推论,并会运用这些知识进行简单的计算和证明.
二、问题导学(阅读教科书第 27-28页,请解答下列问题)
1.什么是圆心角?
(
A
B
C
O
)
2.圆心角的度数与它所对弧的度数是什么关系?
3.如图,△ABC内接于⊙O,这三个内角是圆周角吗?
(1)顶点有什么特征?
圆周角的两边与圆有什么关系?
强调圆周角的两个特征:① ;② 。
(3)概念辨析:判断下图中各个角是不是圆周。
(
O
) (
:
O
O
O
) (
O
) (
O
)
三、合作探究
1、我们已经知道圆心角的度数与它所对弧的度数是相等的,那么圆周角的度数也与它所对弧的度数有关吗?
(
C
A
O
B
)2、同一条弧所对的圆周角与圆心角的度数有关系吗?
3、如图,所对的圆周角∠BAC与圆心角∠BOC,你能得出这两个角的数量关系吗?
4、刚才我们看到的是圆心在圆周角一边时情形,那么圆心与圆周角的位置有哪些情形呢?(画出图示)
5、引导学生把圆心在圆周角的内部和圆心在圆周角的外部这两种情形转化为第一种情形来证明,可让学生交流讨论完成推理过程.
(
A
) (
A
) (
C
C
O
D
O
B
D
)
圆周角定理: .
圆周角的度数 = 同弧所对圆心角的度数的_ ___
推论 1:
推论 2:
能力提升
已知:如图,AB是⊙O的直径,弦CD⊥AB于E,∠ACD=30°,AE=2cm.求DB长.
课堂小结
六、当堂检测
1.如图1,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A.35° B.45° C.55° D.65°
2.如图2所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的度数
是( )
A.80° B.120° C.100 D.90°
3.如图3,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.
若∠BDC=40°,则∠AMB的度数不可能是( )
A.45° B.60° C.75° D.85°
4.在半径为1的⊙O中,弦AB、AC的长分别为和,求∠BAC的度数.
