24.1.1旋转 导学案 2023--2024学年沪科版九年级数学下册(无答案)
文档属性
| 名称 | 24.1.1旋转 导学案 2023--2024学年沪科版九年级数学下册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 188.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览

文档简介
24.1旋转(1)
学习目标
1. 掌握旋转的有关概念及基本性质.(重点)
2. 能够根据旋转的基本性质解决实际问题和进行简单作图.(难点)
二、问题导学(阅读教科书第126-128页,请解答下列问题)
1.旋转的定义:在平面内,一个图形绕着一个 ,旋转一定的 ,得到另一个图形的变换,叫做 . 这个定点叫做 ,转动的角称为 ,点 A旋转后成为点 A',这两个点叫做 .
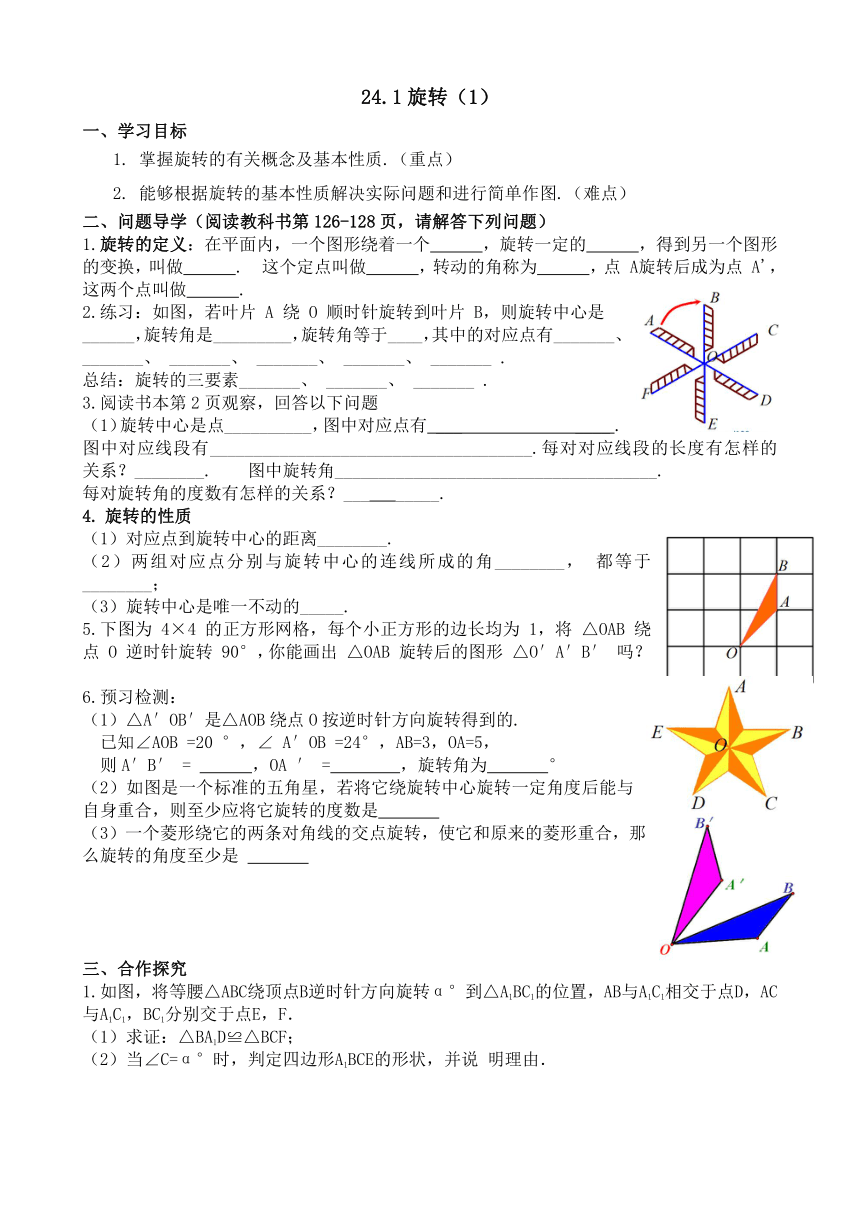
2.练习:如图,若叶片 A 绕 O 顺时针旋转到叶片 B,则旋转中心是______,旋转角是_________,旋转角等于____,其中的对应点有_______、 _______、 _______、 _______、 _______、 _______ .
总结:旋转的三要素_______、 _______、 _______ .
3.阅读书本第2页观察,回答以下问题
(1)旋转中心是点__________,图中对应点有 ___ ____ .
图中对应线段有_____________________________________.每对对应线段的长度有怎样的关系?________. 图中旋转角_____________________________________.
每对旋转角的度数有怎样的关系?___ _____.
旋转的性质
(1)对应点到旋转中心的距离________.
(2)两组对应点分别与旋转中心的连线所成的角________, 都等于________;
(3)旋转中心是唯一不动的_____.
5.下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°,你能画出 △OAB 旋转后的图形 △O′A′B′ 吗?
6.预习检测:
(1)△A′OB′是△AOB绕点O按逆时针方向旋转得到的.
已知∠AOB =20 °,∠ A′OB =24°,AB=3,OA=5,
则A′B′ = ,OA ′ = ,旋转角为 °
(2)如图是一个标准的五角星,若将它绕旋转中心旋转一定角度后能与自身重合,则至少应将它旋转的度数是
(3)一个菱形绕它的两条对角线的交点旋转,使它和原来的菱形重合,那么旋转的角度至少是
三、合作探究
1.如图,将等腰△ABC绕顶点B逆时针方向旋转α°到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E,F.
(1)求证:△BA1D≌△BCF;
(2)当∠C=α°时,判定四边形A1BCE的形状,并说 明理由.
能力提升
如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置,若AE=1,BE=2,CE=3,求∠BE′C.
课堂小结
六、当堂检测
1.下列事件中,属于旋转运动的是 ( )
A.小明向北走了4米 B.小朋友们在荡秋千时做的运动
C.电梯从1楼上升到12楼 D.一物体从高空坠下
2.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向旋转45°而成的. (1)若AB=4,则S正方形A′B′C′D′ = ;
(2) ∠BAB′= ,∠B′AD= .
(3)若连接BB′,则∠ABB′= .
3.如图,将 Rt△ABC 绕点 A 按顺时针方向旋转一定角度得 Rt△ADE,点 B 的对应点 D 恰好落在 BC 边上.若 AC = ,∠B = 60 °,求 CD 的长.
学习目标
1. 掌握旋转的有关概念及基本性质.(重点)
2. 能够根据旋转的基本性质解决实际问题和进行简单作图.(难点)
二、问题导学(阅读教科书第126-128页,请解答下列问题)
1.旋转的定义:在平面内,一个图形绕着一个 ,旋转一定的 ,得到另一个图形的变换,叫做 . 这个定点叫做 ,转动的角称为 ,点 A旋转后成为点 A',这两个点叫做 .
2.练习:如图,若叶片 A 绕 O 顺时针旋转到叶片 B,则旋转中心是______,旋转角是_________,旋转角等于____,其中的对应点有_______、 _______、 _______、 _______、 _______、 _______ .
总结:旋转的三要素_______、 _______、 _______ .
3.阅读书本第2页观察,回答以下问题
(1)旋转中心是点__________,图中对应点有 ___ ____ .
图中对应线段有_____________________________________.每对对应线段的长度有怎样的关系?________. 图中旋转角_____________________________________.
每对旋转角的度数有怎样的关系?___ _____.
旋转的性质
(1)对应点到旋转中心的距离________.
(2)两组对应点分别与旋转中心的连线所成的角________, 都等于________;
(3)旋转中心是唯一不动的_____.
5.下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°,你能画出 △OAB 旋转后的图形 △O′A′B′ 吗?
6.预习检测:
(1)△A′OB′是△AOB绕点O按逆时针方向旋转得到的.
已知∠AOB =20 °,∠ A′OB =24°,AB=3,OA=5,
则A′B′ = ,OA ′ = ,旋转角为 °
(2)如图是一个标准的五角星,若将它绕旋转中心旋转一定角度后能与自身重合,则至少应将它旋转的度数是
(3)一个菱形绕它的两条对角线的交点旋转,使它和原来的菱形重合,那么旋转的角度至少是
三、合作探究
1.如图,将等腰△ABC绕顶点B逆时针方向旋转α°到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E,F.
(1)求证:△BA1D≌△BCF;
(2)当∠C=α°时,判定四边形A1BCE的形状,并说 明理由.
能力提升
如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置,若AE=1,BE=2,CE=3,求∠BE′C.
课堂小结
六、当堂检测
1.下列事件中,属于旋转运动的是 ( )
A.小明向北走了4米 B.小朋友们在荡秋千时做的运动
C.电梯从1楼上升到12楼 D.一物体从高空坠下
2.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向旋转45°而成的. (1)若AB=4,则S正方形A′B′C′D′ = ;
(2) ∠BAB′= ,∠B′AD= .
(3)若连接BB′,则∠ABB′= .
3.如图,将 Rt△ABC 绕点 A 按顺时针方向旋转一定角度得 Rt△ADE,点 B 的对应点 D 恰好落在 BC 边上.若 AC = ,∠B = 60 °,求 CD 的长.
