24.1.2旋转 导学案 2023--2024学年沪科版九年级数学下册(无答案)
文档属性
| 名称 | 24.1.2旋转 导学案 2023--2024学年沪科版九年级数学下册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 195.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览

文档简介
24.1旋转(2)
学习目标
1.能够依据中心对称的性质解决相关作图问题,正确认识什么是中心对称图形,能够判别一个图形是不是中心对称图形。
2.理解中心对称图形与中心对称的区别与联系。 3.能够用旋转知识解决各种问题.
二、问题导学(阅读教科书第4-9页,请解答下列问题)
1.把一个图形_____________________________________________________________那么就说这两个图形关于这个点中心对称。这个点叫_______。
2.结合中心对称的定义回答:①中心对称的图形有____个;②中心对称是把一个图形绕某一点旋转___°③中心对称揭示了_____个图形中的一种_______关系。
3.利用上述性质解答:
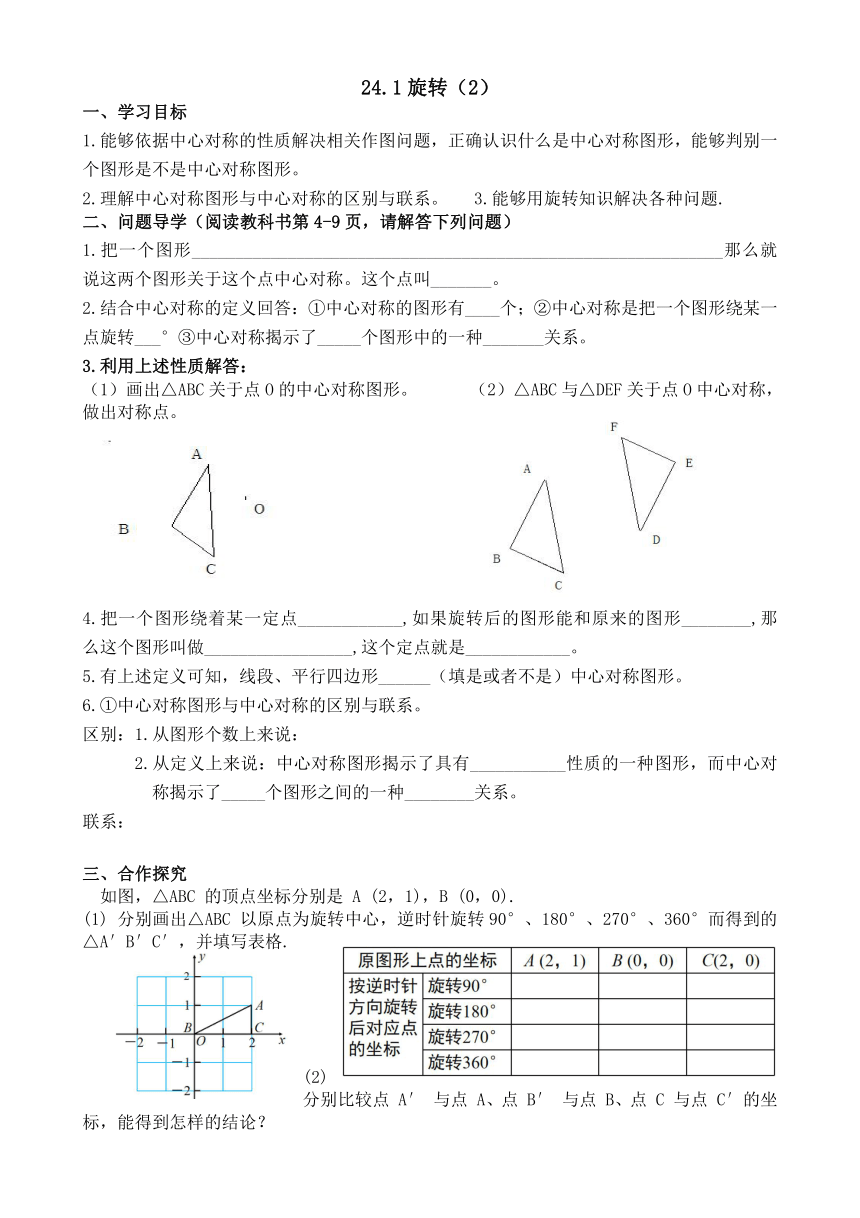
(1)画出△ABC关于点O的中心对称图形。 (2)△ABC与△DEF关于点O中心对称,做出对称点。
4.把一个图形绕着某一定点____________,如果旋转后的图形能和原来的图形________,那么这个图形叫做_________________,这个定点就是____________。
5.有上述定义可知,线段、平行四边形______(填是或者不是)中心对称图形。
6.①中心对称图形与中心对称的区别与联系。
区别:1.从图形个数上来说:
2.从定义上来说:中心对称图形揭示了具有___________性质的一种图形,而中心对称揭示了_____个图形之间的一种________关系。
联系:
三、合作探究
如图,△ABC 的顶点坐标分别是 A (2,1),B (0,0).
(1) 分别画出△ABC 以原点为旋转中心,逆时针旋转90°、180°、270°、360°而得到的△A′B′C′,并填写表格.
(2) 分别比较点 A′ 与点 A、点 B′ 与点 B、点 C 与点 C′的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以坐标原点为旋转中心作几个特殊角度的旋转,可得如下结果:
四、能力提升
如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称
(2)若△ADC的面积为4,求△ABE的面积.
五、课堂小结
六、当堂检测
1.下列四个图形中,是中心对称图形的是 ( )
第2题 第3题
2.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于点E成中心对称,则对称中心点E的坐标是 ( )
A.(3,-1) B.(0,0) C.(2,-1) D.(-1,3)
3.如图,直线EF经过 ABCD的对称中心O,且分别交AB,CD于点E,F.若 ABCD的面积为24 cm2,则图中阴影部分的面积为 cm2.
4.如图,有一腰长为5 cm,底边长为4 cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成四边形,是中心对称图形的有 种.
学习目标
1.能够依据中心对称的性质解决相关作图问题,正确认识什么是中心对称图形,能够判别一个图形是不是中心对称图形。
2.理解中心对称图形与中心对称的区别与联系。 3.能够用旋转知识解决各种问题.
二、问题导学(阅读教科书第4-9页,请解答下列问题)
1.把一个图形_____________________________________________________________那么就说这两个图形关于这个点中心对称。这个点叫_______。
2.结合中心对称的定义回答:①中心对称的图形有____个;②中心对称是把一个图形绕某一点旋转___°③中心对称揭示了_____个图形中的一种_______关系。
3.利用上述性质解答:
(1)画出△ABC关于点O的中心对称图形。 (2)△ABC与△DEF关于点O中心对称,做出对称点。
4.把一个图形绕着某一定点____________,如果旋转后的图形能和原来的图形________,那么这个图形叫做_________________,这个定点就是____________。
5.有上述定义可知,线段、平行四边形______(填是或者不是)中心对称图形。
6.①中心对称图形与中心对称的区别与联系。
区别:1.从图形个数上来说:
2.从定义上来说:中心对称图形揭示了具有___________性质的一种图形,而中心对称揭示了_____个图形之间的一种________关系。
联系:
三、合作探究
如图,△ABC 的顶点坐标分别是 A (2,1),B (0,0).
(1) 分别画出△ABC 以原点为旋转中心,逆时针旋转90°、180°、270°、360°而得到的△A′B′C′,并填写表格.
(2) 分别比较点 A′ 与点 A、点 B′ 与点 B、点 C 与点 C′的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以坐标原点为旋转中心作几个特殊角度的旋转,可得如下结果:
四、能力提升
如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称
(2)若△ADC的面积为4,求△ABE的面积.
五、课堂小结
六、当堂检测
1.下列四个图形中,是中心对称图形的是 ( )
第2题 第3题
2.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于点E成中心对称,则对称中心点E的坐标是 ( )
A.(3,-1) B.(0,0) C.(2,-1) D.(-1,3)
3.如图,直线EF经过 ABCD的对称中心O,且分别交AB,CD于点E,F.若 ABCD的面积为24 cm2,则图中阴影部分的面积为 cm2.
4.如图,有一腰长为5 cm,底边长为4 cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成四边形,是中心对称图形的有 种.
