最新人教版七下数学 5.2.1 平行线(22张PPT)
文档属性
| 名称 | 最新人教版七下数学 5.2.1 平行线(22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 08:15:01 | ||
图片预览





文档简介
(共22张PPT)
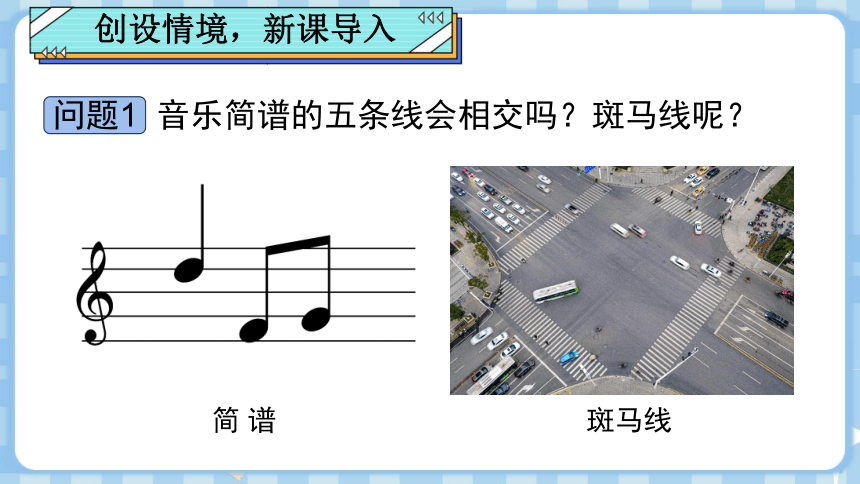
新知一览
线
平行公理及其推论
平
行
线
相
交
线
两条
直线
相交
两条
直线
被第
三条
所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
相交成直角
垂线
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平移
平移的性质
位置
关系
平行线的判定
平行线的性质
(两线四角)
(三线八角)
人教版七年级下册
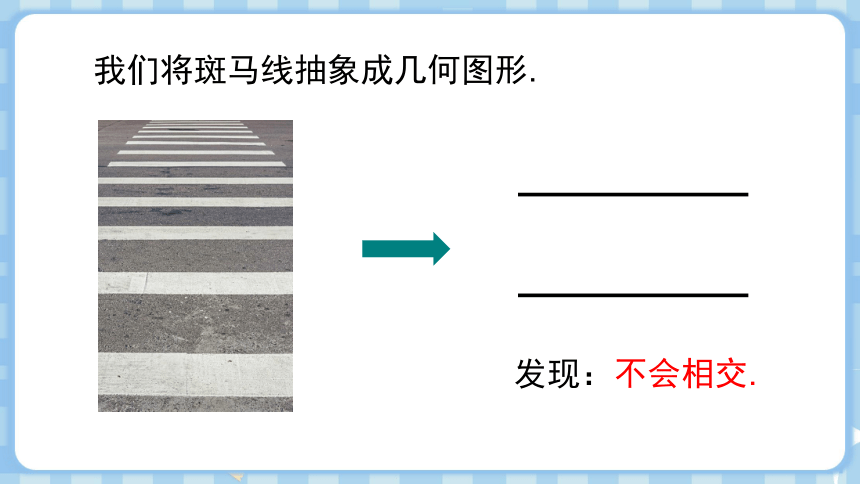
简 谱
问题1 音乐简谱的五条线会相交吗?斑马线呢?
斑马线
创设情境,新课导入
我们将斑马线抽象成几何图形.
发现:不会相交.
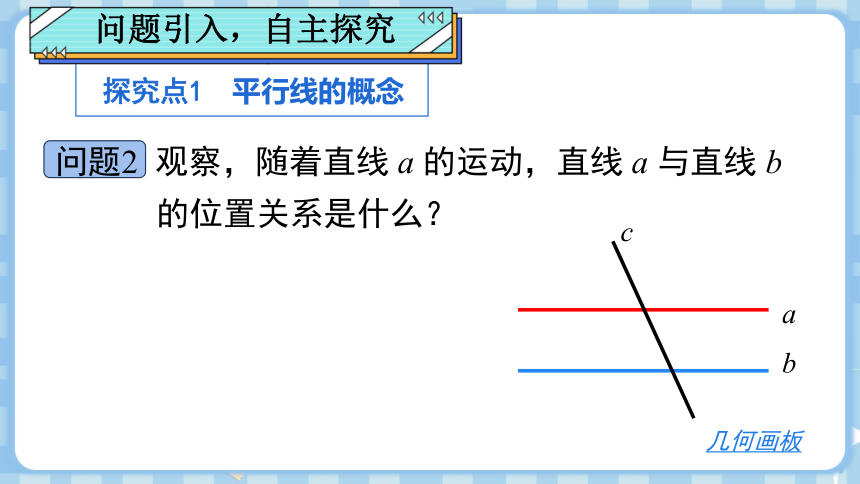
探究点1 平行线的概念
问题2 观察,随着直线 a 的运动,直线 a 与直线 b 的位置关系是什么?
b
a
c
问题引入,自主探究
几何画板
总结
结论:在同一平面内,不重合的两条直线有两种位置关系:相交 和 平行.
定义:同一个平面内,不相交的两条直线互相平行.
b
a
记作:
a ∥ b
读作: a 平行于 b.
A
B
C
D
(AB ∥ CD)
平行线在在生活中是很常见的,你还能举出其他一些例子吗?
对应训练
1. 两条直线相交,交点的个数是______ ;两条直线平行,交点的个数是______ .
1
0
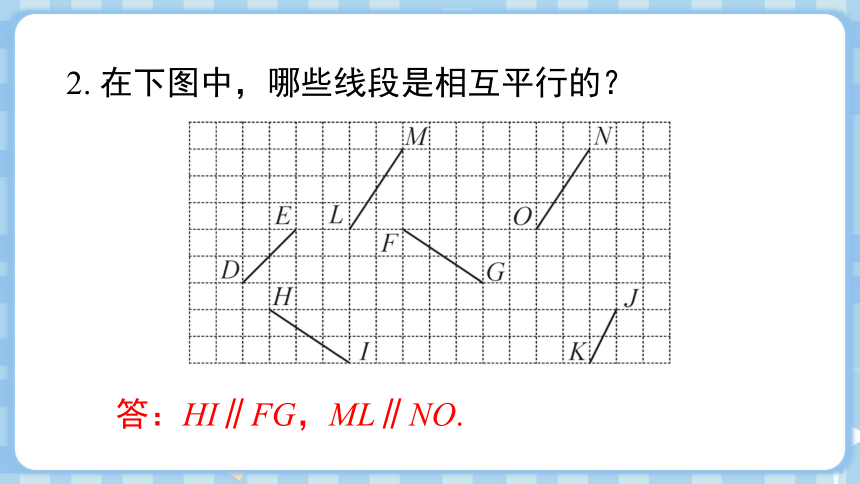
2. 在下图中,哪些线段是相互平行的?
答:HI∥FG,ML∥NO.
a
问题3 如图,已知直线 a 和点 P ,过点 P 画直线 b∥a.想一想,画平行线需要哪几步?
(1)落
(2)靠
(3)移
(4)画
P
探究点2 平行线的画法
b
1.在如图的方格纸中有三条直线 l,m , n ,请在图中分别画出三条直线的平行线,并用符号表示它们.
m
l
n
a
b
c
对应训练
解:如图,a∥m,
b∥l,
c∥n.
C
D
2.读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与直线AB平行;
【教材P12 练习】
A
B
P
(2)直线AB,CD是相交直线,点P是直线AB,CD外的一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E.
A
B
C
D
E
F
P
问题4 如图,过点B画直线 a 的平行线,能画出几条?
再过点C画直线 a 的平行线,它和前面过点B画出的直线平行吗?
B
C
a
你发现了什么?
b
c
探究点3 平行线的公理及其推论
总结
基本事实(平行公理):经过直线外一点,有且只有一条直线与已知直线平行.
B
a
b
总结
B
C
a
b
c
如果两条直线都与第三条直线平行,那么这两条直线互相平行.
符号语言:
如果 b∥a,c∥a,
那么 b∥c.
1.下列说法中正确的有( )
①一条直线的平行线只有一条;
②过一点与已知直线平行的直线有且只有一条;
③因为a∥b,c∥d ,所以a∥d ;
④经过直线外一点,有且只有一条直线与这条直线平行.
A.l个 B.2个 C.3个 D.4个
A
对应训练
2.平面内有A,B,C三点,且三点不在同一条直线上,过三点画两条平行线,这样的平行线能画出几种
A
B
C
A
B
C
A
B
C
①
②
③
例 如图,直线a∥b ,b∥c ,d 与 a 相交于点M.
(1)判断直线a ,c的位置关系:a∥b ,b // c,根据平行公理的推论,得_______;
(2)判断 c 与 d 的位置关系:直线 a 与 d 可以看作经过直线 c 外一点 M 的两条直线,根据平行公理和问题(1)可知 c 与 d 不_______.
a∥c
平行
重点突破,提升探究
如图,若AB//CD,经过点E可画EF// AB,则EF与CD的位置关系是EF// CD,理由是______________
___________________________________________.
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
对应训练
平行线
平行公理及其推论
公理:经过直线外一点,_________一条直线与这条直线平行
平行线及其画法
一放二靠三推四画
记作:_______
有且只有
推论:如果 b∥a,c∥a,那么______
b∥c
a∥b
随堂训练,课堂总结
知识结构
1.教材P15习题5.2第3,8,9题.
作业布置
新知一览
线
平行公理及其推论
平
行
线
相
交
线
两条
直线
相交
两条
直线
被第
三条
所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
相交成直角
垂线
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平移
平移的性质
位置
关系
平行线的判定
平行线的性质
(两线四角)
(三线八角)
人教版七年级下册
简 谱
问题1 音乐简谱的五条线会相交吗?斑马线呢?
斑马线
创设情境,新课导入
我们将斑马线抽象成几何图形.
发现:不会相交.
探究点1 平行线的概念
问题2 观察,随着直线 a 的运动,直线 a 与直线 b 的位置关系是什么?
b
a
c
问题引入,自主探究
几何画板
总结
结论:在同一平面内,不重合的两条直线有两种位置关系:相交 和 平行.
定义:同一个平面内,不相交的两条直线互相平行.
b
a
记作:
a ∥ b
读作: a 平行于 b.
A
B
C
D
(AB ∥ CD)
平行线在在生活中是很常见的,你还能举出其他一些例子吗?
对应训练
1. 两条直线相交,交点的个数是______ ;两条直线平行,交点的个数是______ .
1
0
2. 在下图中,哪些线段是相互平行的?
答:HI∥FG,ML∥NO.
a
问题3 如图,已知直线 a 和点 P ,过点 P 画直线 b∥a.想一想,画平行线需要哪几步?
(1)落
(2)靠
(3)移
(4)画
P
探究点2 平行线的画法
b
1.在如图的方格纸中有三条直线 l,m , n ,请在图中分别画出三条直线的平行线,并用符号表示它们.
m
l
n
a
b
c
对应训练
解:如图,a∥m,
b∥l,
c∥n.
C
D
2.读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与直线AB平行;
【教材P12 练习】
A
B
P
(2)直线AB,CD是相交直线,点P是直线AB,CD外的一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E.
A
B
C
D
E
F
P
问题4 如图,过点B画直线 a 的平行线,能画出几条?
再过点C画直线 a 的平行线,它和前面过点B画出的直线平行吗?
B
C
a
你发现了什么?
b
c
探究点3 平行线的公理及其推论
总结
基本事实(平行公理):经过直线外一点,有且只有一条直线与已知直线平行.
B
a
b
总结
B
C
a
b
c
如果两条直线都与第三条直线平行,那么这两条直线互相平行.
符号语言:
如果 b∥a,c∥a,
那么 b∥c.
1.下列说法中正确的有( )
①一条直线的平行线只有一条;
②过一点与已知直线平行的直线有且只有一条;
③因为a∥b,c∥d ,所以a∥d ;
④经过直线外一点,有且只有一条直线与这条直线平行.
A.l个 B.2个 C.3个 D.4个
A
对应训练
2.平面内有A,B,C三点,且三点不在同一条直线上,过三点画两条平行线,这样的平行线能画出几种
A
B
C
A
B
C
A
B
C
①
②
③
例 如图,直线a∥b ,b∥c ,d 与 a 相交于点M.
(1)判断直线a ,c的位置关系:a∥b ,b // c,根据平行公理的推论,得_______;
(2)判断 c 与 d 的位置关系:直线 a 与 d 可以看作经过直线 c 外一点 M 的两条直线,根据平行公理和问题(1)可知 c 与 d 不_______.
a∥c
平行
重点突破,提升探究
如图,若AB//CD,经过点E可画EF// AB,则EF与CD的位置关系是EF// CD,理由是______________
___________________________________________.
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
对应训练
平行线
平行公理及其推论
公理:经过直线外一点,_________一条直线与这条直线平行
平行线及其画法
一放二靠三推四画
记作:_______
有且只有
推论:如果 b∥a,c∥a,那么______
b∥c
a∥b
随堂训练,课堂总结
知识结构
1.教材P15习题5.2第3,8,9题.
作业布置
