最新人教版七下数学 5.2.2 第1课时平行线的判定 课件(共28张PPT)
文档属性
| 名称 | 最新人教版七下数学 5.2.2 第1课时平行线的判定 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 22:54:29 | ||
图片预览




文档简介
(共28张PPT)
新知一览
线
平行公理及其推论
平
行
线
相
交
线
两条
直线
相交
两条
直线
被第
三条
所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
相交成直角
垂线
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平移
平移的性质
位置
关系
平行线的判定
平行线的性质
(两线四角)
(三线八角)
5.2.2 平行线的判定
人教版七年级下册
如何判断两条直线平行?
双杠
楼梯扶手
还有其他方法吗?
在同一平面内,两条不相交的直线互相平行.
创设情境,新课导入
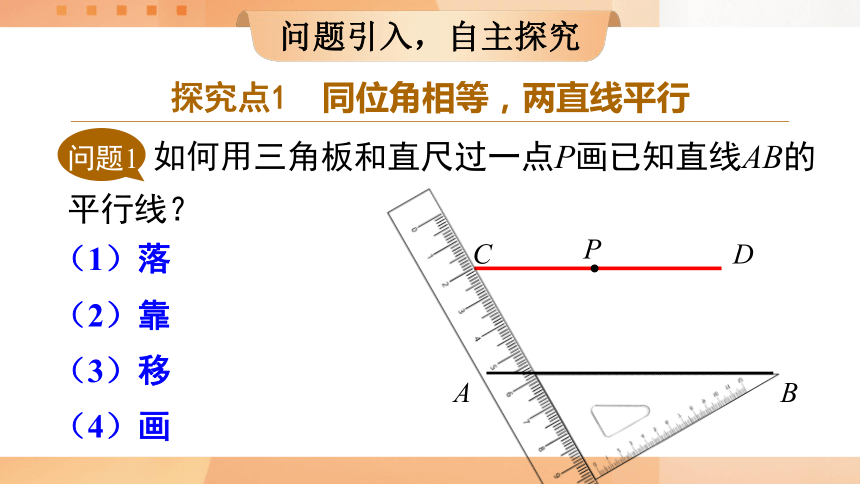
问题1 如何用三角板和直尺过一点P画已知直线AB的平行线?
探究点1 同位角相等,两直线平行
(1)落
(2)靠
(3)移
(4)画
P
A
B
C
D
问题引入,自主探究
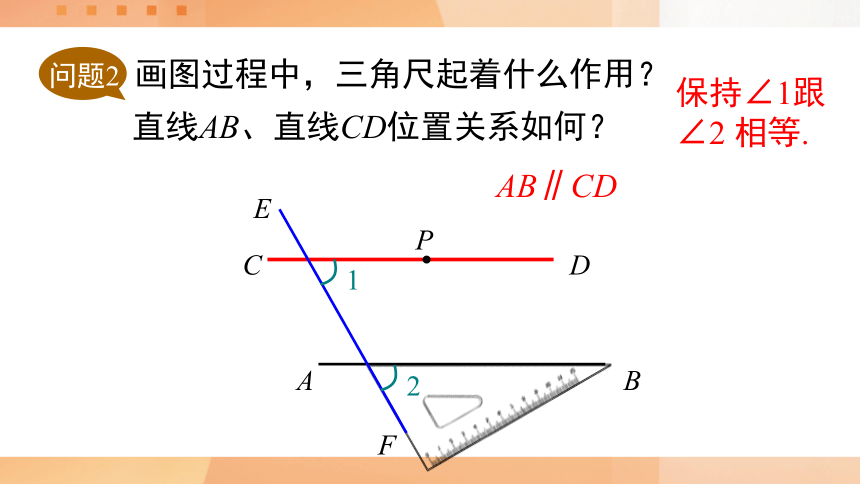
问题2 画图过程中,三角尺起着什么作用?
直线AB、直线CD位置关系如何?
P
A
B
C
D
1
2
保持∠1跟∠2 相等.
AB∥CD
E
F
总结
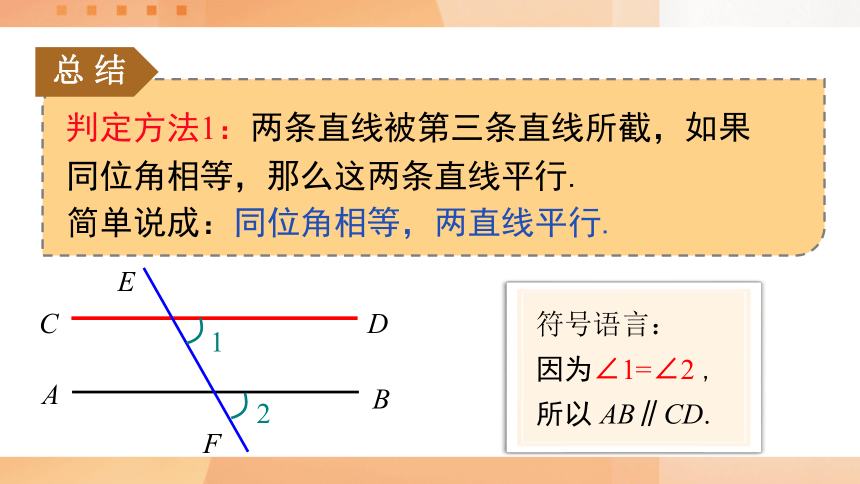
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
A
B
C
D
1
2
E
F
符号语言:
因为∠1=∠2 ,
所以 AB∥CD.
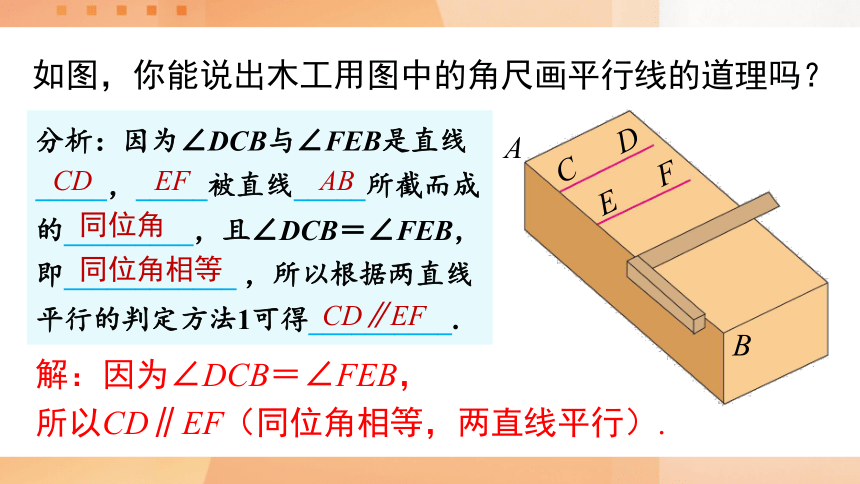
如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
解:因为∠DCB=∠FEB,
所以CD∥EF(同位角相等,两直线平行).
分析:因为∠DCB与∠FEB是直线_____,_____被直线_____所截而成的_________,且∠DCB=∠FEB,即____________ ,所以根据两直线平行的判定方法1可得__________.
CD
EF
AB
同位角
同位角相等
CD∥EF
1.如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB//CD的是( )
A.∠2=35° B.∠2=45°
C.∠2=55° D.∠2=125°
C
对应训练
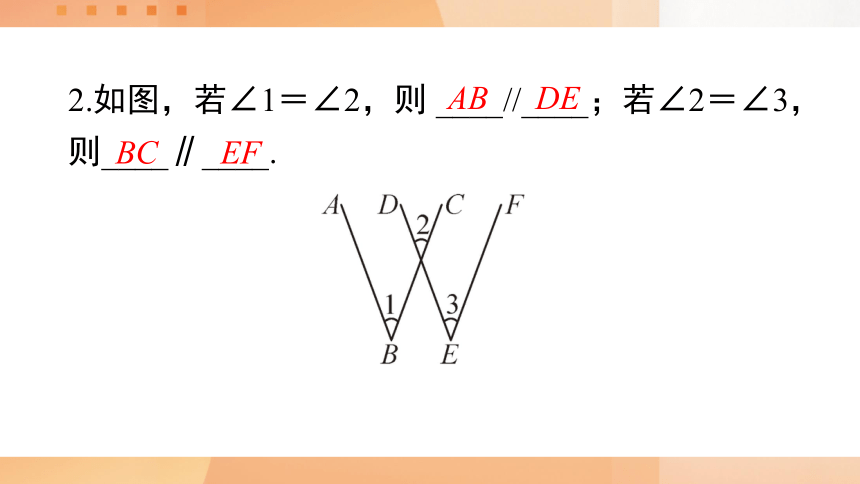
2.如图,若∠1=∠2,则 ____//____;若∠2=∠3,则____∥____.
AB
DE
BC
EF
a
b
c
1
2
3
4
分析:
两条直线平行
判定
内错角、同旁内角
将其转化成同位角相等,即可判定两直线平行
问题3 能否利用内错角,或同旁内角来判定两条直线平行呢?
问题4 如果∠2 = ∠3,能得出 a∥b 吗?
解:因为∠2 =∠3(已知条件),
∠1=∠3(对顶角相等),
所以∠2=∠1(等量代换).
所以a∥b (同位角相等,两直线平行).
探究点2 内错角相等,两直线平行
a
b
c
1
2
3
4
总结
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
符号语言:
因为∠2=∠3 ,
所以 a∥b.
a
b
c
2
3
1.如图是一条街道的两个拐角,若∠ABC与∠BCD均为140°,则街道AB与CD的位置关系是_________.
AB//CD
对应训练
2.将两个相同的三角板如图摆放,画直线a,b,则a//b,理由是:_________________________.
内错角相等,两直线平行
问题5 如果∠2+∠4=180°,能得出 a∥ b 吗?请分组讨论并归纳定义.
a
b
c
1
2
3
4
解:如果∠2 +∠4=180°(已知),
∠1+∠4=180°(邻补角的定义),
所以∠1=∠2(同角的补角相等).
所以a∥b (同位角相等,两直线平行).
探究点3 同旁内角互补,两直线平行
总结
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
a
b
c
2
4
符号语言:
因为∠2+∠4=180° ,
所以 a∥b.
拓展 如果∠2+∠4=180°,请利用判定方法2说明同旁内角互补,两直线平行.
a
b
c
1
2
3
4
解:因为∠2 +∠4=180°(已知),
∠3+∠4=180°(邻补角的定义),
所以∠2=∠3(同角的补角相等).
所以a∥b (内错角相等,两直线平行).
1.如图,一个弯形管道ABCD的拐角∠ABC=110°,要使管道AB,CD保持平行,则∠BCD的度数为( )
A.110°
B.120°
C.70°
D.80°
C
对应训练
2.如图,一块折断的零件左边AC 断口整齐,右边BD形状不规则,工人小李测得左边∠A=45°,∠C=135°,他由此断定这个零件另外的一组对边AB∥CD,他的依据是_________________________.
同旁内角互补,两直线平行
例 (1)如图,当∠1=∠3时,直线a,b平行吗
(2)当∠2+∠3=180°时,直线a,b平行吗 为什么
解:(1)因为∠1=∠3,∠3=∠4,
所以∠1=∠4.
所以a // b(同位角相等,两直线平行).
重点突破,提升探究
(2)因为∠3=∠4,∠2=∠5,
∠2+∠3=180°,
所以∠5+∠4=180°.
所以 a // b (同旁内角互补,两直线平行).
1.如图,下列条件能判定直线l1∥l2的是 ( )
A.∠1=∠2
B.∠1+∠3=180°
C.∠4=∠5
D.∠3=∠5
B
对应训练
2.如图,
(1)∵∠B=∠3,
∴____∥_____,
根据的是______________________;
(2)∵∠2=∠A,
∴____∥_____,
根据的是______________________;
∵→“因为”
∴→“所以”
AB
CE
同位角相等,两直线平行
AB
CE
内错角相等,两直线平行
(3)∵∠2=∠E,
∴____∥_____,
根据的是_______________________;
(4)∵∠B+∠BCE=180°,
∴____∥_____,
根据的是________________________;
AC
DE
内错角相等,两直线平行
AB
CE
同旁内角互补,两直线平行
3.如图,BE是AB的延长线.
(1)由∠CBE=∠A可以判定哪两条直线平行
根据是什么
A
B
E
D
C
答:(1)AD∥BC,根据是“同位角相等,两直线平行”;
【教材P14 练习 第1题】
(2)由∠CBE=∠C可以判定哪两条直线平行
根据是什么
(2)DC∥AB,根据是“内错角相等,两直线平行”;
A
B
E
D
C
平行线的判定
判定方法
__________,两直线平行
定义法
同一个平面内,两条直线_______
同位角相等
____________,两直线平行
同旁内角互补
不相交
__________,两直线平行
内错角相等
随堂训练,课堂总结
知识结构
1.教材P15习题5.2第1,2,4,5题.
作业布置
新知一览
线
平行公理及其推论
平
行
线
相
交
线
两条
直线
相交
两条
直线
被第
三条
所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
相交成直角
垂线
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平移
平移的性质
位置
关系
平行线的判定
平行线的性质
(两线四角)
(三线八角)
5.2.2 平行线的判定
人教版七年级下册
如何判断两条直线平行?
双杠
楼梯扶手
还有其他方法吗?
在同一平面内,两条不相交的直线互相平行.
创设情境,新课导入
问题1 如何用三角板和直尺过一点P画已知直线AB的平行线?
探究点1 同位角相等,两直线平行
(1)落
(2)靠
(3)移
(4)画
P
A
B
C
D
问题引入,自主探究
问题2 画图过程中,三角尺起着什么作用?
直线AB、直线CD位置关系如何?
P
A
B
C
D
1
2
保持∠1跟∠2 相等.
AB∥CD
E
F
总结
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
A
B
C
D
1
2
E
F
符号语言:
因为∠1=∠2 ,
所以 AB∥CD.
如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
解:因为∠DCB=∠FEB,
所以CD∥EF(同位角相等,两直线平行).
分析:因为∠DCB与∠FEB是直线_____,_____被直线_____所截而成的_________,且∠DCB=∠FEB,即____________ ,所以根据两直线平行的判定方法1可得__________.
CD
EF
AB
同位角
同位角相等
CD∥EF
1.如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB//CD的是( )
A.∠2=35° B.∠2=45°
C.∠2=55° D.∠2=125°
C
对应训练
2.如图,若∠1=∠2,则 ____//____;若∠2=∠3,则____∥____.
AB
DE
BC
EF
a
b
c
1
2
3
4
分析:
两条直线平行
判定
内错角、同旁内角
将其转化成同位角相等,即可判定两直线平行
问题3 能否利用内错角,或同旁内角来判定两条直线平行呢?
问题4 如果∠2 = ∠3,能得出 a∥b 吗?
解:因为∠2 =∠3(已知条件),
∠1=∠3(对顶角相等),
所以∠2=∠1(等量代换).
所以a∥b (同位角相等,两直线平行).
探究点2 内错角相等,两直线平行
a
b
c
1
2
3
4
总结
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
符号语言:
因为∠2=∠3 ,
所以 a∥b.
a
b
c
2
3
1.如图是一条街道的两个拐角,若∠ABC与∠BCD均为140°,则街道AB与CD的位置关系是_________.
AB//CD
对应训练
2.将两个相同的三角板如图摆放,画直线a,b,则a//b,理由是:_________________________.
内错角相等,两直线平行
问题5 如果∠2+∠4=180°,能得出 a∥ b 吗?请分组讨论并归纳定义.
a
b
c
1
2
3
4
解:如果∠2 +∠4=180°(已知),
∠1+∠4=180°(邻补角的定义),
所以∠1=∠2(同角的补角相等).
所以a∥b (同位角相等,两直线平行).
探究点3 同旁内角互补,两直线平行
总结
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
a
b
c
2
4
符号语言:
因为∠2+∠4=180° ,
所以 a∥b.
拓展 如果∠2+∠4=180°,请利用判定方法2说明同旁内角互补,两直线平行.
a
b
c
1
2
3
4
解:因为∠2 +∠4=180°(已知),
∠3+∠4=180°(邻补角的定义),
所以∠2=∠3(同角的补角相等).
所以a∥b (内错角相等,两直线平行).
1.如图,一个弯形管道ABCD的拐角∠ABC=110°,要使管道AB,CD保持平行,则∠BCD的度数为( )
A.110°
B.120°
C.70°
D.80°
C
对应训练
2.如图,一块折断的零件左边AC 断口整齐,右边BD形状不规则,工人小李测得左边∠A=45°,∠C=135°,他由此断定这个零件另外的一组对边AB∥CD,他的依据是_________________________.
同旁内角互补,两直线平行
例 (1)如图,当∠1=∠3时,直线a,b平行吗
(2)当∠2+∠3=180°时,直线a,b平行吗 为什么
解:(1)因为∠1=∠3,∠3=∠4,
所以∠1=∠4.
所以a // b(同位角相等,两直线平行).
重点突破,提升探究
(2)因为∠3=∠4,∠2=∠5,
∠2+∠3=180°,
所以∠5+∠4=180°.
所以 a // b (同旁内角互补,两直线平行).
1.如图,下列条件能判定直线l1∥l2的是 ( )
A.∠1=∠2
B.∠1+∠3=180°
C.∠4=∠5
D.∠3=∠5
B
对应训练
2.如图,
(1)∵∠B=∠3,
∴____∥_____,
根据的是______________________;
(2)∵∠2=∠A,
∴____∥_____,
根据的是______________________;
∵→“因为”
∴→“所以”
AB
CE
同位角相等,两直线平行
AB
CE
内错角相等,两直线平行
(3)∵∠2=∠E,
∴____∥_____,
根据的是_______________________;
(4)∵∠B+∠BCE=180°,
∴____∥_____,
根据的是________________________;
AC
DE
内错角相等,两直线平行
AB
CE
同旁内角互补,两直线平行
3.如图,BE是AB的延长线.
(1)由∠CBE=∠A可以判定哪两条直线平行
根据是什么
A
B
E
D
C
答:(1)AD∥BC,根据是“同位角相等,两直线平行”;
【教材P14 练习 第1题】
(2)由∠CBE=∠C可以判定哪两条直线平行
根据是什么
(2)DC∥AB,根据是“内错角相等,两直线平行”;
A
B
E
D
C
平行线的判定
判定方法
__________,两直线平行
定义法
同一个平面内,两条直线_______
同位角相等
____________,两直线平行
同旁内角互补
不相交
__________,两直线平行
内错角相等
随堂训练,课堂总结
知识结构
1.教材P15习题5.2第1,2,4,5题.
作业布置
