最新人教版七下数学 5.3.1 第2课时 平行线的判定与性质的综合运用 课件(共19张PPT)
文档属性
| 名称 | 最新人教版七下数学 5.3.1 第2课时 平行线的判定与性质的综合运用 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
平行线判定与
性质的综合运用
5.3.1 平行线的性质
R·七年级数学下册
类别 文字语言 符号语言 图形
判定 ① 同位角相等,两直线平行 ∵∠1=∠3, ∴a∥b.
② 内错角相等,两直线平行 ∵∠2=∠4, ∴a∥b. ③ 同旁内角互补,两直线平行 ∵∠2+∠3=180°, ∴a∥b. 复习回顾
类别 文字语言 符号语言 图形
性质 ① 两直线平行,同位角相等 ∵a∥b. ∴∠1=∠3,
② 两直线平行,内错角相等 ∵a∥b, ∴∠2=∠4. ③ 两直线平行,同旁内角互补 ∵a∥b, ∴∠2+∠3=180°. 复习回顾
思考:平行线的判定方法和性质有什么区别与联系?
探究点 平行线的判定与性质的综合运用
①如图,已知∠1=∠2,∠D=50°,求∠B的度数.
解:∵∠1=∠2(已知),∠2=∠DHE(对顶角相等),
∴∠1=∠DHE(等量代换).
∴AB∥CD (同位角相等,两直线平行).
∴∠B+∠D =180°(两直线平行,同旁内角互补).
∵∠D=50°(已知),
∴∠B=180°-∠D=180°-50°=130°.
探索新知
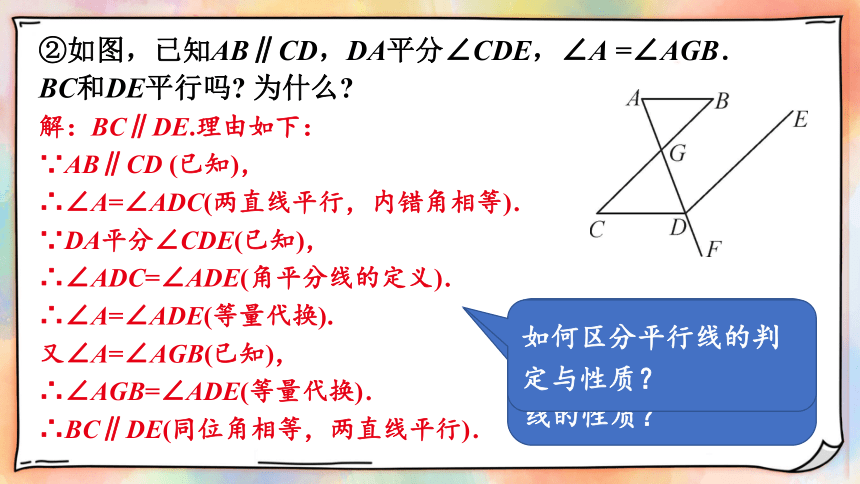
②如图,已知AB∥CD,DA平分∠CDE,∠A =∠AGB.
BC和DE平行吗 为什么
解:BC∥DE.理由如下:
∵AB∥CD (已知),
∴∠A=∠ADC(两直线平行,内错角相等).
∵DA平分∠CDE(已知),
∴∠ADC=∠ADE(角平分线的定义).
∴∠A=∠ADE(等量代换).
又∠A=∠AGB(已知),
∴∠AGB=∠ADE(等量代换).
∴BC∥DE(同位角相等,两直线平行).
哪些属于平行线的判定?哪些又属于平行线的性质?
如何区分平行线的判定与性质?
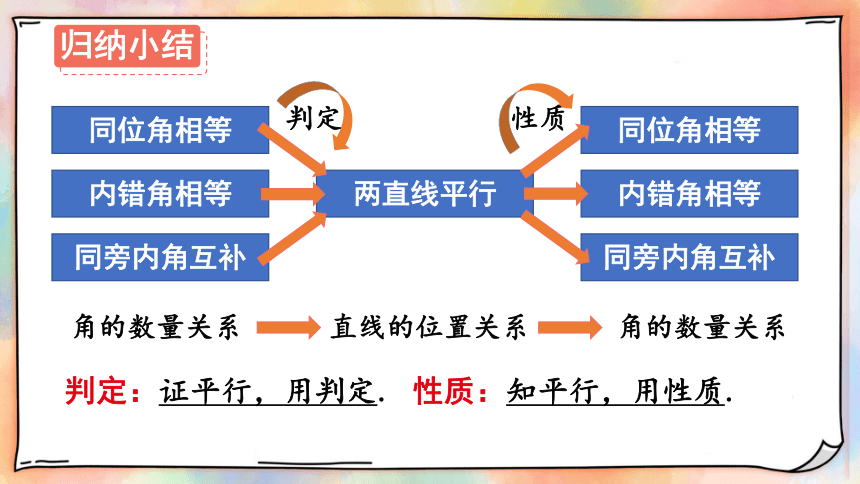
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
角的数量关系
直线的位置关系
角的数量关系
判定:证平行,用判定.
性质:知平行,用性质.
归纳小结
1.如图,直线EF分别与直线AB,CD相交于点G,H,已知∠1=∠2=70°,GM平分∠HGB交直线CD于点M,则∠3=( ).
A.50° B.55° C.60° D.62°
B
对应训练
2.如图,已知∠1+∠2=180°,∠3=∠B.
(1)AB 与EF平行吗 为什么
(2)若∠BGD=55°,DE平分∠ADG,求∠1的度数.
解:(1)平行.理由:
∵∠1+∠2=180°(已知),
∠1+∠DFE=180°(邻补角的定义),
∴∠2=∠DFE(同角的补角相等).
∴AB∥EF(内错角相等,两直线平行).
(2)由(1)可知AB∥EF,
∴∠3=∠ADE(两直线平行,内错角相等).
又∠3=∠B(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠EDG=∠BGD=55°(两直线平行,内错角相等).
∵DE平分∠ADG(已知),
∴∠ADG=2∠EDG=110°(角平分线的定义).
又AB∥EF,
∴∠1=∠ADG=110°(两直线平行,同位角相等).
3.如图,三角形ABC 中,D 是 AB 上一点,E 是 AC 上一点, ∠ADE = 60°,∠B = 60°,∠AED = 40°.
(1)DE 和 BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
【选自教材第20页 练习 第2题】
解:(1)∵∠ADE = ∠B,∴DE∥BC(同位角相等,两直线平行)
(2)∵DE∥BC,∴∠C = ∠AED = 40°(两直线平行,同位角相等)
4.已知:如图,∠1+∠B=∠C.试说明BD∥CE.
解:如图,作射线AP,使AP∥BD,∴∠PAB=∠B(两直线平行,内错角相等).
又∠1+∠B=∠C(已知),
∴∠1+∠PAB=∠C(等量代换),
即∠PAC=∠C.
∴AP∥CE(内错角相等,两直线平行).
又AP∥BD,
∴BD∥CE(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
P
1.一个大门栏杆的平面示意图如图所示,BA 垂直于地面AE 于点A,CD平行于地面AE.若∠BCD=150°,则∠ABC=______.
120°
随堂练习
2.(1)如图①,已知直线AB∥CD,点P 位于AB,CD之间,则∠AEP,∠CFP,∠EPF之间存在怎样的数量关系,请说明理由.小明想到了以下方法,请帮助他完成推理过程:
解:∠AEP+∠CFP=∠EPF.理由如下:
如图①,过点P 作PG∥AB,
则∠AEP=∠_____(_______________________).
∵AB∥CD,
∴PG∥______(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠CFP=∠_____(_______________________).
又∠EPG+∠FPG=∠_______,
∴∠AEP+∠CFP=∠EPF.
EPG
两直线平行,内错角相等
CD
FPG
两直线平行,内错角相等
EPF
(2)如图②,AB∥CD,请写出∠AEP,∠EPF,∠CFP 之间的数量关系,并说明理由.
解:∠AEP+∠EPF+∠CFP=360°.理由如下:
如图②,过点P作PM∥AB,
则∠AEP+∠EPM=180°(两直线平行,同旁内角互补).∵AB∥CD,
∴PM∥CD (如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠CFP+∠FPM =180°(两直线平行,同旁内角互补).
∴∠AEP+∠EPM+∠FPM +∠CFP=360°,
即∠AEP+∠EPF+∠CFP=360°.
M
如图,点E在AB上,点F在CD上,CE,BF分别交AD于点G,H.已知∠A =∠AGE,∠D=∠DGC.
(1)AB与CD平行吗 请说明理由.
(2)若∠2+∠1=180°,且∠BEC=2∠B+30°,求∠C的度数.
解:(1)AB∥CD.理由如下:
∵∠A=∠AGE,∠D=∠DGC,∠AGE=∠DGC(对顶角相等),∴∠A=∠D (等量代换).
∴AB∥CD (内错角相等,两直线平行).
拓展提升
(2)∵∠2+∠1=180°,∠1=∠AHB(对顶角相等),∴∠2+∠AHB=180°(等量代换).
∴CE∥BF(同旁内角互补,两直线平行).
∴∠B+∠BEC=180°(两直线平行,同旁内角互补),∠B=∠AEC(两直线平行,同位角相等).
∵∠BEC=2∠B+30°,
∴∠B+2∠B+30°=180°(等量代换).
∴∠B=50°.
由(1)可知AB∥CD,∴∠AEC=∠C(两直线平行,内错角相等).
∴∠C=∠B=50°(等量代换).
同位角相等
内错角相等
同旁内角互补
判定
性质
两直线平行
课堂小结
《练习册》主体部分相应课时训练.
课后作业
平行线判定与
性质的综合运用
5.3.1 平行线的性质
R·七年级数学下册
类别 文字语言 符号语言 图形
判定 ① 同位角相等,两直线平行 ∵∠1=∠3, ∴a∥b.
② 内错角相等,两直线平行 ∵∠2=∠4, ∴a∥b. ③ 同旁内角互补,两直线平行 ∵∠2+∠3=180°, ∴a∥b. 复习回顾
类别 文字语言 符号语言 图形
性质 ① 两直线平行,同位角相等 ∵a∥b. ∴∠1=∠3,
② 两直线平行,内错角相等 ∵a∥b, ∴∠2=∠4. ③ 两直线平行,同旁内角互补 ∵a∥b, ∴∠2+∠3=180°. 复习回顾
思考:平行线的判定方法和性质有什么区别与联系?
探究点 平行线的判定与性质的综合运用
①如图,已知∠1=∠2,∠D=50°,求∠B的度数.
解:∵∠1=∠2(已知),∠2=∠DHE(对顶角相等),
∴∠1=∠DHE(等量代换).
∴AB∥CD (同位角相等,两直线平行).
∴∠B+∠D =180°(两直线平行,同旁内角互补).
∵∠D=50°(已知),
∴∠B=180°-∠D=180°-50°=130°.
探索新知
②如图,已知AB∥CD,DA平分∠CDE,∠A =∠AGB.
BC和DE平行吗 为什么
解:BC∥DE.理由如下:
∵AB∥CD (已知),
∴∠A=∠ADC(两直线平行,内错角相等).
∵DA平分∠CDE(已知),
∴∠ADC=∠ADE(角平分线的定义).
∴∠A=∠ADE(等量代换).
又∠A=∠AGB(已知),
∴∠AGB=∠ADE(等量代换).
∴BC∥DE(同位角相等,两直线平行).
哪些属于平行线的判定?哪些又属于平行线的性质?
如何区分平行线的判定与性质?
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
角的数量关系
直线的位置关系
角的数量关系
判定:证平行,用判定.
性质:知平行,用性质.
归纳小结
1.如图,直线EF分别与直线AB,CD相交于点G,H,已知∠1=∠2=70°,GM平分∠HGB交直线CD于点M,则∠3=( ).
A.50° B.55° C.60° D.62°
B
对应训练
2.如图,已知∠1+∠2=180°,∠3=∠B.
(1)AB 与EF平行吗 为什么
(2)若∠BGD=55°,DE平分∠ADG,求∠1的度数.
解:(1)平行.理由:
∵∠1+∠2=180°(已知),
∠1+∠DFE=180°(邻补角的定义),
∴∠2=∠DFE(同角的补角相等).
∴AB∥EF(内错角相等,两直线平行).
(2)由(1)可知AB∥EF,
∴∠3=∠ADE(两直线平行,内错角相等).
又∠3=∠B(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠EDG=∠BGD=55°(两直线平行,内错角相等).
∵DE平分∠ADG(已知),
∴∠ADG=2∠EDG=110°(角平分线的定义).
又AB∥EF,
∴∠1=∠ADG=110°(两直线平行,同位角相等).
3.如图,三角形ABC 中,D 是 AB 上一点,E 是 AC 上一点, ∠ADE = 60°,∠B = 60°,∠AED = 40°.
(1)DE 和 BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
【选自教材第20页 练习 第2题】
解:(1)∵∠ADE = ∠B,∴DE∥BC(同位角相等,两直线平行)
(2)∵DE∥BC,∴∠C = ∠AED = 40°(两直线平行,同位角相等)
4.已知:如图,∠1+∠B=∠C.试说明BD∥CE.
解:如图,作射线AP,使AP∥BD,∴∠PAB=∠B(两直线平行,内错角相等).
又∠1+∠B=∠C(已知),
∴∠1+∠PAB=∠C(等量代换),
即∠PAC=∠C.
∴AP∥CE(内错角相等,两直线平行).
又AP∥BD,
∴BD∥CE(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
P
1.一个大门栏杆的平面示意图如图所示,BA 垂直于地面AE 于点A,CD平行于地面AE.若∠BCD=150°,则∠ABC=______.
120°
随堂练习
2.(1)如图①,已知直线AB∥CD,点P 位于AB,CD之间,则∠AEP,∠CFP,∠EPF之间存在怎样的数量关系,请说明理由.小明想到了以下方法,请帮助他完成推理过程:
解:∠AEP+∠CFP=∠EPF.理由如下:
如图①,过点P 作PG∥AB,
则∠AEP=∠_____(_______________________).
∵AB∥CD,
∴PG∥______(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠CFP=∠_____(_______________________).
又∠EPG+∠FPG=∠_______,
∴∠AEP+∠CFP=∠EPF.
EPG
两直线平行,内错角相等
CD
FPG
两直线平行,内错角相等
EPF
(2)如图②,AB∥CD,请写出∠AEP,∠EPF,∠CFP 之间的数量关系,并说明理由.
解:∠AEP+∠EPF+∠CFP=360°.理由如下:
如图②,过点P作PM∥AB,
则∠AEP+∠EPM=180°(两直线平行,同旁内角互补).∵AB∥CD,
∴PM∥CD (如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠CFP+∠FPM =180°(两直线平行,同旁内角互补).
∴∠AEP+∠EPM+∠FPM +∠CFP=360°,
即∠AEP+∠EPF+∠CFP=360°.
M
如图,点E在AB上,点F在CD上,CE,BF分别交AD于点G,H.已知∠A =∠AGE,∠D=∠DGC.
(1)AB与CD平行吗 请说明理由.
(2)若∠2+∠1=180°,且∠BEC=2∠B+30°,求∠C的度数.
解:(1)AB∥CD.理由如下:
∵∠A=∠AGE,∠D=∠DGC,∠AGE=∠DGC(对顶角相等),∴∠A=∠D (等量代换).
∴AB∥CD (内错角相等,两直线平行).
拓展提升
(2)∵∠2+∠1=180°,∠1=∠AHB(对顶角相等),∴∠2+∠AHB=180°(等量代换).
∴CE∥BF(同旁内角互补,两直线平行).
∴∠B+∠BEC=180°(两直线平行,同旁内角互补),∠B=∠AEC(两直线平行,同位角相等).
∵∠BEC=2∠B+30°,
∴∠B+2∠B+30°=180°(等量代换).
∴∠B=50°.
由(1)可知AB∥CD,∴∠AEC=∠C(两直线平行,内错角相等).
∴∠C=∠B=50°(等量代换).
同位角相等
内错角相等
同旁内角互补
判定
性质
两直线平行
课堂小结
《练习册》主体部分相应课时训练.
课后作业
