人教版七下数学 7.1.2 平面直角坐标系 课件(共38张PPT)
文档属性
| 名称 | 人教版七下数学 7.1.2 平面直角坐标系 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览






文档简介
(共38张PPT)
7.1.2 平面直角坐标系
人教版七年级(下)
(1)在平面内,确定物体的位置一般需要几个数据 有哪些方法
在平面内,确定物体的位置一般需要两个数据.
常用的方法:用有序数对来确定,如:(排,列),(组,排),
(排,号),(角度,距离),(纬度,经度)等.
(2)什么是数轴?
规定了原点、正方向、单位长度的直线就构成了数轴.
回顾导入
-4
-3
-2
-1
0
1
2
3
4
思考1:如图,数轴上的点A、B表示的数是什么?表示数字4的点是哪个点?
A:-3
B:2
点C
B
A
C
思考2:由思考1你发现数轴上的点与实数之间有什么关系?
回顾导入
①数轴上的每个点都对应一个实数(这个实数叫作这个点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
数轴上的点与实数之间存在着一一对应的关系.
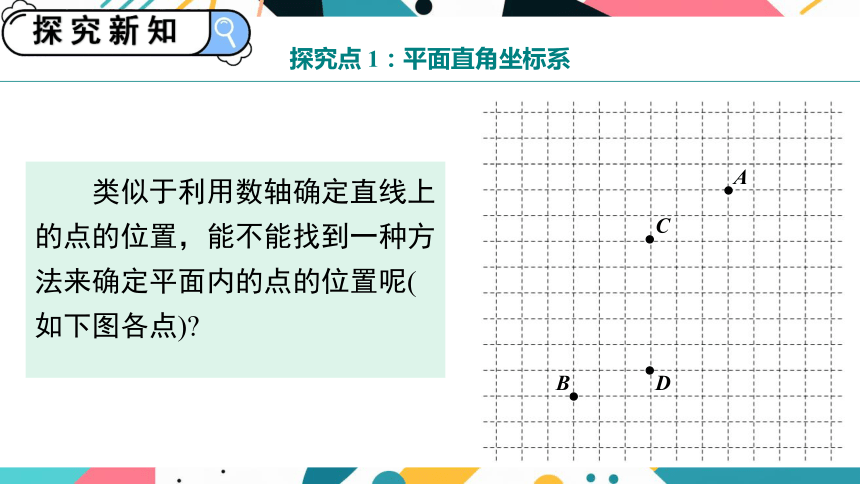
探究点 1:平面直角坐标系
类似于利用数轴确定直线上的点的位置,能不能找到一种方法来确定平面内的点的位置呢(如下图各点)
A
B
C
D
探究新知
A
B
C
D
探究新知
x
y
O
水平的数轴叫x轴或横轴,习惯上取向右为正方向
平面内画两条________,原点________的数轴,组成平面直角坐标系.
重合
互相垂直
两坐标轴的交点为平面直角坐标系的原点
竖直的数轴叫y轴或纵轴,取向上为正方向
M
N
A
B
C
D
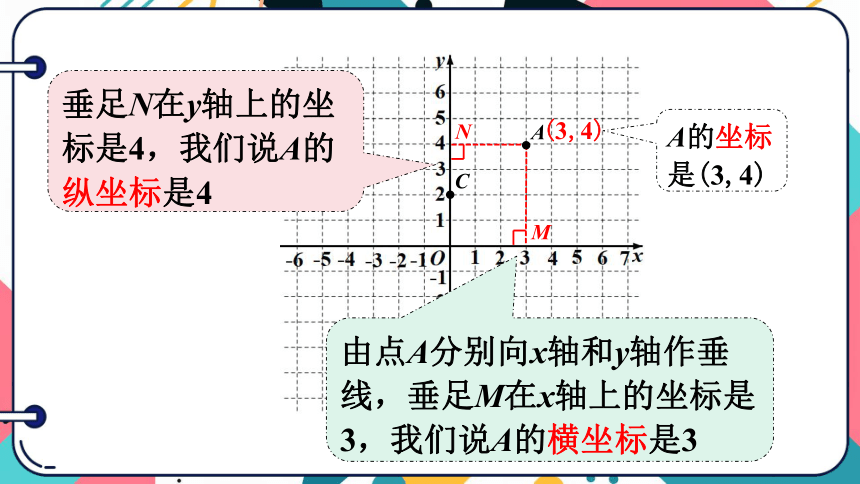
(3,4)
由点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是3,我们说A的横坐标是3
垂足N在y轴上的坐标是4,我们说A的纵坐标是4
A的坐标是(3,4)
M
N
A
B
C
D
(3,4)
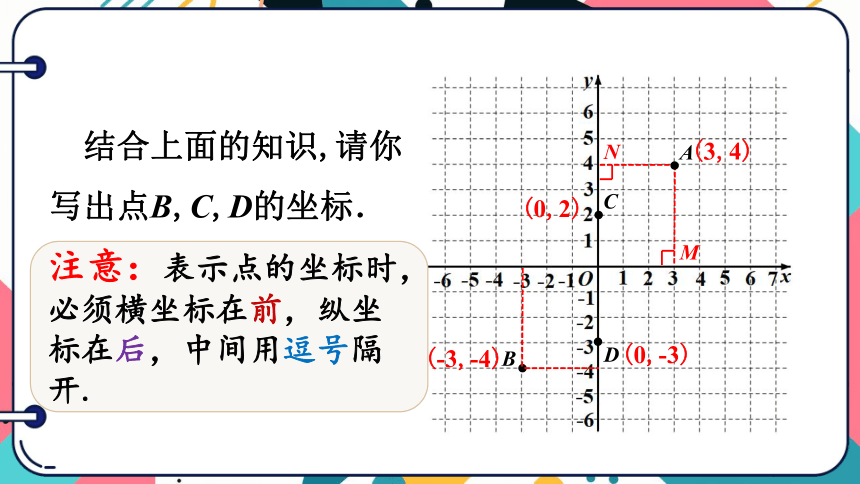
结合上面的知识,请你写出点B,C,D的坐标.
(-3,-4)
(0,2)
(0,-3)
注意:表示点的坐标时,必须横坐标在前,纵坐标在后,中间用逗号隔开.
确定点的坐标
过点画垂线
纵坐标:画 x 轴垂线
横坐标:画 y 轴垂线
归纳总结
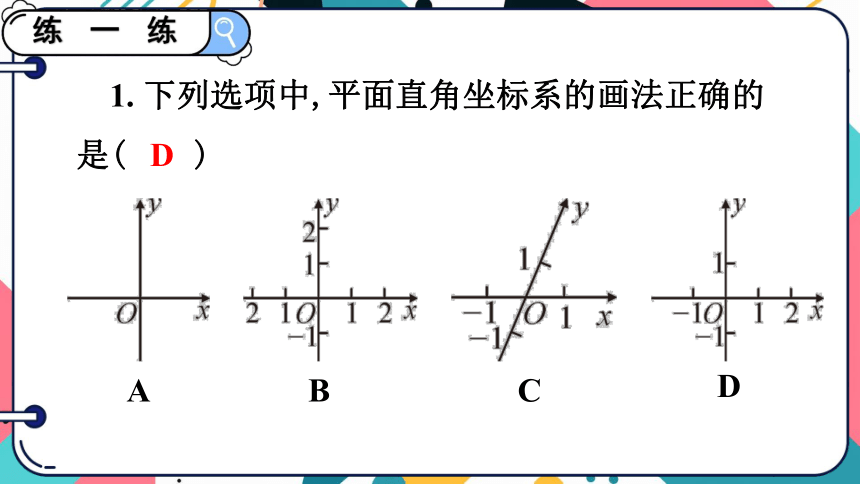
1. 下列选项中,平面直角坐标系的画法正确的
是( )
D
D
C
B
A
练一练
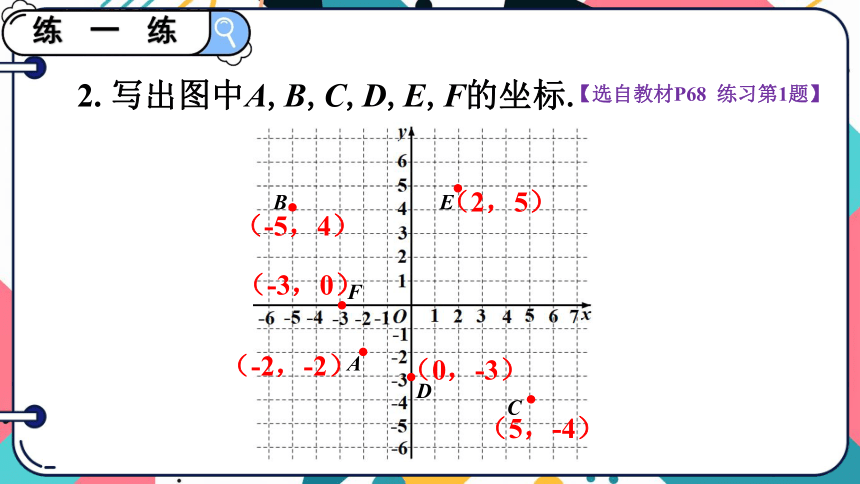
2. 写出图中A,B,C,D,E,F的坐标.
【选自教材P68 练习第1题】
A
B
C
D
(-2,-2)
(-5,4)
F
E
(5,-4)
(0,-3)
(2,5)
(-3,0)
练一练
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分,每个部分称为象限(如图),分别叫做第一象限、第二象限、第三象限和第四象限.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
探究点2:平面直角坐标系中的点的坐标特征
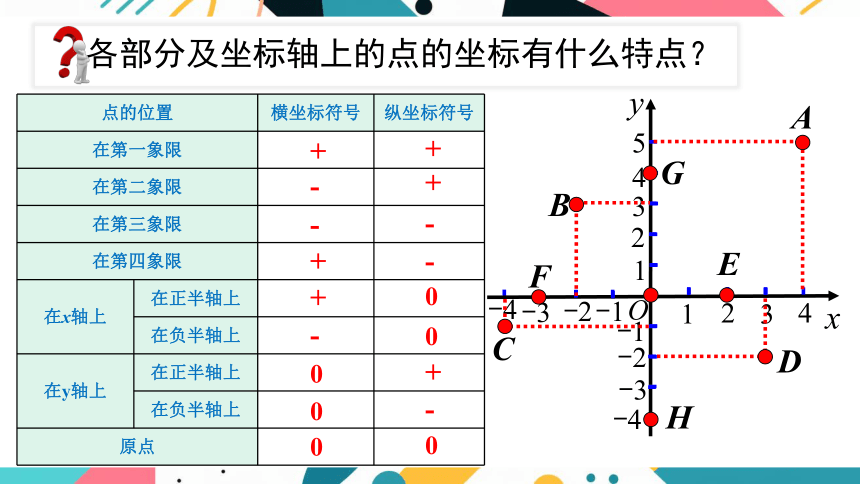
各部分及坐标轴上的点的坐标有什么特点?
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
A
B
C
D
H
E
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
+
+
-
+
-
-
-
+
+
0
0
-
0
0
+
-
0
0
F
G
在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限或哪条坐标轴上:
(1)点P(x,y)的坐标满足xy>0;
(2)点P(x,y)的坐标满足xy<0;
(3)点P(x,y)的坐标满足xy=0.
【选自教材P71 习题7.1 第10题】
第一象限或第三象限
第二象限或第四象限
x轴或y轴上
练一练
例1 在平面直角坐标系中描出下列各点:
A(4,5), B(-2,3),
C(-4,-1),D(2.5,-2),
E(0,-4).
解:如图,先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是点A. 类似地,可在图上描出点B,C,D,E.
A(4,5)
B(-2,3)
D(2.5,-2)
C(-4,-1)
E(0,-4)
1 2 3 4 5 x
-5 -4 -3 -2 -1O
5 4 3 2 1
-1 -2 -3 -4 -5
y
典例精析
有序实数对
(即点的坐标)
一一对应
坐标平面内的点
平面直角坐标系中的点到坐标轴的距离:点到x轴的距离是该点纵坐标的绝对值;点到y轴的距离是该点横坐标的绝对值.
归纳总结
1. 在图中描出下列各点:
L(-5,-3), M(4,0),
N(-6,2),P(5,-3.5),
Q(0,5),R(6,2).
解:如图所示.
L
1 2 3 4 5 6 x
5 4 3 2 1
-1 -2 -3 -4 -5
y
-6 -5 -4 -3 -2 -1O
M
N
P
Q
R
【选自教材P68 练习第2题】
练一练
2. 在平面直角坐标系中,若点A(m2-4,m+1) 在y轴的非负半轴上,则点B(m-1,1-2m) 在第____象限.
四
m2 -4=0
分析:
m=2
m +1>0
B(1,-3)
m-1=1
1-2m=-3
练一练
(1)如图,正方形ABCD的边长为6,如果以点A为原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线 写出正方形的顶点A,B,C,D的坐标.
A(O)
B
C
D
(0,0)
x
y
(6,0)
(0,6)
(6,6)
探究点 3:以图形顶点为原点建立不同的平面直角坐标系
A
B
C
D
(0,0)
x
y
(-6,0)
(0,6)
(-6,6)
(O)
(2)请在图中另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是多少 与同学们交流一下.
解:如图所示.
巩固已知点的位置的坐标,平面直角坐标系不同,所求点的坐标也不同.
在规则的几何图形中一般优先考虑顶点、边长等建立直角坐标系.
归纳总结
定义
点
平面直角坐标系
在平面内,两条互相垂直、_____重合的数轴组成平面直角坐标系
向 x 轴画垂线
(垂足对应数a)
原点
象限
向 y 轴画垂线
(垂足对应数b)
一个有
序数对
点的坐标
_____
(a,b)
点的 位置 第一 象限 第二 象限 第三 象限 第四
象限
x 符号
y 符号
+
+
-
+
-
-
+
-
课堂总结
1.教材P69 习题 7.1 第2,3,4,5,6,7,8,9,11,12,
13,14题.
课后作业
1. 根据点所在的位置,用“+” “-”填表.
【选自教材P69 习题7.1 第2题】
点的位置 横坐标符号 纵坐标符号
在第一象限 + +
在第二象限 - +
在第三象限 - -
在第四象限 + -
课后作业
如图,写出其中标有字母的各点的坐标,并指出它们的横坐标和纵坐标.
【选自教材P69 习题7.1 第3题】
A
B
C
D
E
F
G
解:
A(-5,4),横坐标:-5,纵坐标:4;
B(-2,2),横坐标:-2,纵坐标:2;
C(3,4),横坐标:3,纵坐标:4;
D(2,1),横坐标:2,纵坐标:1;
E(5,-3),横坐标:5,纵坐标:-3;
F(-1,-2),横坐标:-1,纵坐标:-2;
G(-5,-3),横坐标:-5,纵坐标:-3;
课后作业
3. 在平面直角坐标系中,描出下列各点:
点A在y轴上,位于原点上方,距离原点2个单位长度;
点B在x轴上,位于原点右侧,距离原点1个单位长度;
点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;
点D在x轴上,位于原点右侧,距离原点3个单位长度;
点E在x轴上方,y轴右侧,距离x轴2个单位长度,距离y轴4
个单位长度. 依次连接这些点,你能得到什么图形?
【选自教材P69 习题7.1 第4题】
课后作业
x
y
O
1 2 3 4
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
A
B
C
D
E
解:如图,图形类似于英文字母“W”.
课后作业
如图,在所给的坐标系中描出下列各点:
A(-4,-4),B(-2,-2),
C(3,3), D(5,5),
E(-3,-3),F(0,0).
这些点有什么关系?你能再找出一些类似
的点吗?
【选自教材P70 习题7.1 第5题】
-4 -3 -2 -1
x
y
O
1 2 3 4 5
54
3
2
1
-1
-2
-3
-4
解:如图,这些点横纵坐标相等,且在同一条直线上;如:(-1,-1),(1,1),(2,2)等.
A
B
E
D
C
(F)
D
课后作业
如图,建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(4,0),写出点A,D,E,F,G的坐标,并指出它们所在的象限.
【选自教材P70 习题7.1 第6题】
x
y
O
1 2 3 4 5 6 7
54
3
2
1
-3 -2 -1
-1
A
B
C
D
E
F
G
解:建立的平面直角坐标系如图,A(-2,3)在第二象限,D(6,1)在第一象限,E(5,3)在第一象限,F(3,2)在第一象限,G(1,5)在第一象限.
课后作业
6. 在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
(1)(-5,0),(-4,3),(-3,0),(-2,3),(-1,0),(-5,0);
(2)(2,1),(6,1),(6,3),(7,3),(4,6),(1,3),(2,3),(2,1).
观察得到的图形,你觉得它们像什么?求出所得到图形的面积.
【选自教材P70 习题7.1 第7题】
课后作业
y
O
1 2 3 4 5 6 7
-6 -5 -4 -3 -2 -1
O
x
y
4 3 2 1
(-5,0)
(-2,3)
(-3,0)
(-4,3)
(-1,0)
65 4 3 2 1
x
(1,3)
(4,6)
(2,3)
(2,1)
(6,1)
(6,3)
(7,3)
像两个三角形
S= ×2×3×2=6
像房子
S=4×2+ ×6×3=17
课后作业
7. 建立一个平面直角坐标系,描出点A(-2,4),B(3,4),画直线AB.若点C为直线AB上的任意一点,则点C的纵坐标是什么?想一想:
(1)如果一些点在平行于x轴的直线上,那么这些点的纵坐标有什么特点?
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标有什么特点?
【选自教材P70 习题7.1 第8题】
课后作业
解:如图,若C为直线AB上的任意一点,则点C的纵坐标是4.
(1)如果一些点在平行于x轴的直线上,那么这些点的纵坐标都相同.
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标都相同.
O
-3 -2 -1 1 2 3
432 1
x
-1 -2
A
B
y
课后作业
8. 李强同学家在学校以东1 000m再往北1 500m处,张明同学家在学校以西2 000m再往南500m处,王玲同学家在学校以南1 500m处.如图,在坐标系(规定一个单位长度代表1m长)中画出这三位同学家的位置,并用坐标表示出来.
【选自教材P70 习题7.1 第9题】
y/m
O
x/m
500
500
学校
北
李强
张明
王玲
解:如图,李强(1000,1500),
张明(-2000,-500),
王玲(0,-1500).
课后作业
9. 图中正方形(实线)四条边上横坐标、纵坐标都为整数的点有几个?写出它们的坐标.
【选自教材P71 习题7.1 第11题】
y
O
-3 -2 -1 1 2 3
32 1
x
-1 -2 -3
解:有12个.(0,3),(1,2),
(2,1),(3,0),(2,-1),(1,-2),(0,-3),(-1,-2),(-2,-1),(-3,0),(-2,1),(-1,2).
课后作业
10. 如图,右图是由左图平移后得到的图形,找几对特殊的对应点,分别写出它们的坐标,你能发现什么规律吗?
【选自教材P71 习题7.1 第13题】
解:头顶坐标分别为(-4,6),(5,6);
左眼坐标分别为(-5,4),(4,4);
右眼坐标分别为(-3,4),(6,4);
下巴坐标分别为(-4,1),(5,1).
这些对应点的坐标,横坐标差9个单位
长度,纵坐标分别相等.
课后作业
11. 已知点O(0,0),B(1,2) ,点A在坐标轴上,
且S△OAB=2,求满足条件的点A的坐标.
S△OAB =2
分析:
点A在x轴上
O(0,0) B(1,2)
|xA|=2
点A在y轴上
|yA|=4
A(2,0) 或(-2,0)
A(0,4)或(0,-4)
【选自教材P71 习题7.1 第14题】
解:若点A在x轴上时,
则S△OAB= ·|yB|·|xA|= ×2×|xA|=2.
∴xA=±2,∴A(2,0)或(-2,0);
若点A在y轴上时,
则S△OAB= ·|xB|·|yA|= ×1×|yA|=2.
∴yA=±4,∴A(0,4)或(0,-4).
∴满足条件的点A的坐标为:
(2,0)、(-2,0)、(0,4)和(0,-4).
13. 设计一个容易用它的顶点坐标描绘出来的图形,把这些坐标告诉你的同学,看看他能否画出你所设计的图形.
【选自教材P71 习题7.1 第12题】
课后作业
7.1.2 平面直角坐标系
人教版七年级(下)
(1)在平面内,确定物体的位置一般需要几个数据 有哪些方法
在平面内,确定物体的位置一般需要两个数据.
常用的方法:用有序数对来确定,如:(排,列),(组,排),
(排,号),(角度,距离),(纬度,经度)等.
(2)什么是数轴?
规定了原点、正方向、单位长度的直线就构成了数轴.
回顾导入
-4
-3
-2
-1
0
1
2
3
4
思考1:如图,数轴上的点A、B表示的数是什么?表示数字4的点是哪个点?
A:-3
B:2
点C
B
A
C
思考2:由思考1你发现数轴上的点与实数之间有什么关系?
回顾导入
①数轴上的每个点都对应一个实数(这个实数叫作这个点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
数轴上的点与实数之间存在着一一对应的关系.
探究点 1:平面直角坐标系
类似于利用数轴确定直线上的点的位置,能不能找到一种方法来确定平面内的点的位置呢(如下图各点)
A
B
C
D
探究新知
A
B
C
D
探究新知
x
y
O
水平的数轴叫x轴或横轴,习惯上取向右为正方向
平面内画两条________,原点________的数轴,组成平面直角坐标系.
重合
互相垂直
两坐标轴的交点为平面直角坐标系的原点
竖直的数轴叫y轴或纵轴,取向上为正方向
M
N
A
B
C
D
(3,4)
由点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是3,我们说A的横坐标是3
垂足N在y轴上的坐标是4,我们说A的纵坐标是4
A的坐标是(3,4)
M
N
A
B
C
D
(3,4)
结合上面的知识,请你写出点B,C,D的坐标.
(-3,-4)
(0,2)
(0,-3)
注意:表示点的坐标时,必须横坐标在前,纵坐标在后,中间用逗号隔开.
确定点的坐标
过点画垂线
纵坐标:画 x 轴垂线
横坐标:画 y 轴垂线
归纳总结
1. 下列选项中,平面直角坐标系的画法正确的
是( )
D
D
C
B
A
练一练
2. 写出图中A,B,C,D,E,F的坐标.
【选自教材P68 练习第1题】
A
B
C
D
(-2,-2)
(-5,4)
F
E
(5,-4)
(0,-3)
(2,5)
(-3,0)
练一练
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分,每个部分称为象限(如图),分别叫做第一象限、第二象限、第三象限和第四象限.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
探究点2:平面直角坐标系中的点的坐标特征
各部分及坐标轴上的点的坐标有什么特点?
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
A
B
C
D
H
E
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
+
+
-
+
-
-
-
+
+
0
0
-
0
0
+
-
0
0
F
G
在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限或哪条坐标轴上:
(1)点P(x,y)的坐标满足xy>0;
(2)点P(x,y)的坐标满足xy<0;
(3)点P(x,y)的坐标满足xy=0.
【选自教材P71 习题7.1 第10题】
第一象限或第三象限
第二象限或第四象限
x轴或y轴上
练一练
例1 在平面直角坐标系中描出下列各点:
A(4,5), B(-2,3),
C(-4,-1),D(2.5,-2),
E(0,-4).
解:如图,先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是点A. 类似地,可在图上描出点B,C,D,E.
A(4,5)
B(-2,3)
D(2.5,-2)
C(-4,-1)
E(0,-4)
1 2 3 4 5 x
-5 -4 -3 -2 -1O
5 4 3 2 1
-1 -2 -3 -4 -5
y
典例精析
有序实数对
(即点的坐标)
一一对应
坐标平面内的点
平面直角坐标系中的点到坐标轴的距离:点到x轴的距离是该点纵坐标的绝对值;点到y轴的距离是该点横坐标的绝对值.
归纳总结
1. 在图中描出下列各点:
L(-5,-3), M(4,0),
N(-6,2),P(5,-3.5),
Q(0,5),R(6,2).
解:如图所示.
L
1 2 3 4 5 6 x
5 4 3 2 1
-1 -2 -3 -4 -5
y
-6 -5 -4 -3 -2 -1O
M
N
P
Q
R
【选自教材P68 练习第2题】
练一练
2. 在平面直角坐标系中,若点A(m2-4,m+1) 在y轴的非负半轴上,则点B(m-1,1-2m) 在第____象限.
四
m2 -4=0
分析:
m=2
m +1>0
B(1,-3)
m-1=1
1-2m=-3
练一练
(1)如图,正方形ABCD的边长为6,如果以点A为原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线 写出正方形的顶点A,B,C,D的坐标.
A(O)
B
C
D
(0,0)
x
y
(6,0)
(0,6)
(6,6)
探究点 3:以图形顶点为原点建立不同的平面直角坐标系
A
B
C
D
(0,0)
x
y
(-6,0)
(0,6)
(-6,6)
(O)
(2)请在图中另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是多少 与同学们交流一下.
解:如图所示.
巩固已知点的位置的坐标,平面直角坐标系不同,所求点的坐标也不同.
在规则的几何图形中一般优先考虑顶点、边长等建立直角坐标系.
归纳总结
定义
点
平面直角坐标系
在平面内,两条互相垂直、_____重合的数轴组成平面直角坐标系
向 x 轴画垂线
(垂足对应数a)
原点
象限
向 y 轴画垂线
(垂足对应数b)
一个有
序数对
点的坐标
_____
(a,b)
点的 位置 第一 象限 第二 象限 第三 象限 第四
象限
x 符号
y 符号
+
+
-
+
-
-
+
-
课堂总结
1.教材P69 习题 7.1 第2,3,4,5,6,7,8,9,11,12,
13,14题.
课后作业
1. 根据点所在的位置,用“+” “-”填表.
【选自教材P69 习题7.1 第2题】
点的位置 横坐标符号 纵坐标符号
在第一象限 + +
在第二象限 - +
在第三象限 - -
在第四象限 + -
课后作业
如图,写出其中标有字母的各点的坐标,并指出它们的横坐标和纵坐标.
【选自教材P69 习题7.1 第3题】
A
B
C
D
E
F
G
解:
A(-5,4),横坐标:-5,纵坐标:4;
B(-2,2),横坐标:-2,纵坐标:2;
C(3,4),横坐标:3,纵坐标:4;
D(2,1),横坐标:2,纵坐标:1;
E(5,-3),横坐标:5,纵坐标:-3;
F(-1,-2),横坐标:-1,纵坐标:-2;
G(-5,-3),横坐标:-5,纵坐标:-3;
课后作业
3. 在平面直角坐标系中,描出下列各点:
点A在y轴上,位于原点上方,距离原点2个单位长度;
点B在x轴上,位于原点右侧,距离原点1个单位长度;
点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;
点D在x轴上,位于原点右侧,距离原点3个单位长度;
点E在x轴上方,y轴右侧,距离x轴2个单位长度,距离y轴4
个单位长度. 依次连接这些点,你能得到什么图形?
【选自教材P69 习题7.1 第4题】
课后作业
x
y
O
1 2 3 4
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
A
B
C
D
E
解:如图,图形类似于英文字母“W”.
课后作业
如图,在所给的坐标系中描出下列各点:
A(-4,-4),B(-2,-2),
C(3,3), D(5,5),
E(-3,-3),F(0,0).
这些点有什么关系?你能再找出一些类似
的点吗?
【选自教材P70 习题7.1 第5题】
-4 -3 -2 -1
x
y
O
1 2 3 4 5
54
3
2
1
-1
-2
-3
-4
解:如图,这些点横纵坐标相等,且在同一条直线上;如:(-1,-1),(1,1),(2,2)等.
A
B
E
D
C
(F)
D
课后作业
如图,建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(4,0),写出点A,D,E,F,G的坐标,并指出它们所在的象限.
【选自教材P70 习题7.1 第6题】
x
y
O
1 2 3 4 5 6 7
54
3
2
1
-3 -2 -1
-1
A
B
C
D
E
F
G
解:建立的平面直角坐标系如图,A(-2,3)在第二象限,D(6,1)在第一象限,E(5,3)在第一象限,F(3,2)在第一象限,G(1,5)在第一象限.
课后作业
6. 在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
(1)(-5,0),(-4,3),(-3,0),(-2,3),(-1,0),(-5,0);
(2)(2,1),(6,1),(6,3),(7,3),(4,6),(1,3),(2,3),(2,1).
观察得到的图形,你觉得它们像什么?求出所得到图形的面积.
【选自教材P70 习题7.1 第7题】
课后作业
y
O
1 2 3 4 5 6 7
-6 -5 -4 -3 -2 -1
O
x
y
4 3 2 1
(-5,0)
(-2,3)
(-3,0)
(-4,3)
(-1,0)
65 4 3 2 1
x
(1,3)
(4,6)
(2,3)
(2,1)
(6,1)
(6,3)
(7,3)
像两个三角形
S= ×2×3×2=6
像房子
S=4×2+ ×6×3=17
课后作业
7. 建立一个平面直角坐标系,描出点A(-2,4),B(3,4),画直线AB.若点C为直线AB上的任意一点,则点C的纵坐标是什么?想一想:
(1)如果一些点在平行于x轴的直线上,那么这些点的纵坐标有什么特点?
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标有什么特点?
【选自教材P70 习题7.1 第8题】
课后作业
解:如图,若C为直线AB上的任意一点,则点C的纵坐标是4.
(1)如果一些点在平行于x轴的直线上,那么这些点的纵坐标都相同.
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标都相同.
O
-3 -2 -1 1 2 3
432 1
x
-1 -2
A
B
y
课后作业
8. 李强同学家在学校以东1 000m再往北1 500m处,张明同学家在学校以西2 000m再往南500m处,王玲同学家在学校以南1 500m处.如图,在坐标系(规定一个单位长度代表1m长)中画出这三位同学家的位置,并用坐标表示出来.
【选自教材P70 习题7.1 第9题】
y/m
O
x/m
500
500
学校
北
李强
张明
王玲
解:如图,李强(1000,1500),
张明(-2000,-500),
王玲(0,-1500).
课后作业
9. 图中正方形(实线)四条边上横坐标、纵坐标都为整数的点有几个?写出它们的坐标.
【选自教材P71 习题7.1 第11题】
y
O
-3 -2 -1 1 2 3
32 1
x
-1 -2 -3
解:有12个.(0,3),(1,2),
(2,1),(3,0),(2,-1),(1,-2),(0,-3),(-1,-2),(-2,-1),(-3,0),(-2,1),(-1,2).
课后作业
10. 如图,右图是由左图平移后得到的图形,找几对特殊的对应点,分别写出它们的坐标,你能发现什么规律吗?
【选自教材P71 习题7.1 第13题】
解:头顶坐标分别为(-4,6),(5,6);
左眼坐标分别为(-5,4),(4,4);
右眼坐标分别为(-3,4),(6,4);
下巴坐标分别为(-4,1),(5,1).
这些对应点的坐标,横坐标差9个单位
长度,纵坐标分别相等.
课后作业
11. 已知点O(0,0),B(1,2) ,点A在坐标轴上,
且S△OAB=2,求满足条件的点A的坐标.
S△OAB =2
分析:
点A在x轴上
O(0,0) B(1,2)
|xA|=2
点A在y轴上
|yA|=4
A(2,0) 或(-2,0)
A(0,4)或(0,-4)
【选自教材P71 习题7.1 第14题】
解:若点A在x轴上时,
则S△OAB= ·|yB|·|xA|= ×2×|xA|=2.
∴xA=±2,∴A(2,0)或(-2,0);
若点A在y轴上时,
则S△OAB= ·|xB|·|yA|= ×1×|yA|=2.
∴yA=±4,∴A(0,4)或(0,-4).
∴满足条件的点A的坐标为:
(2,0)、(-2,0)、(0,4)和(0,-4).
13. 设计一个容易用它的顶点坐标描绘出来的图形,把这些坐标告诉你的同学,看看他能否画出你所设计的图形.
【选自教材P71 习题7.1 第12题】
课后作业
