最新人教版七下数学 第五章 相交线与平行线 章末复习(31张PPT)
文档属性
| 名称 | 最新人教版七下数学 第五章 相交线与平行线 章末复习(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 08:20:33 | ||
图片预览







文档简介
(共31张PPT)
人教版·七年级下册
5
本章复习
相交线
两条直线相交
邻补角、对顶角
垂线及其性质
点到直线的距离
两条直线被第三条直线所截
同位角、内错角、同旁内角
平行线
平 移
平行公理
判定
性质
本章知识结构图
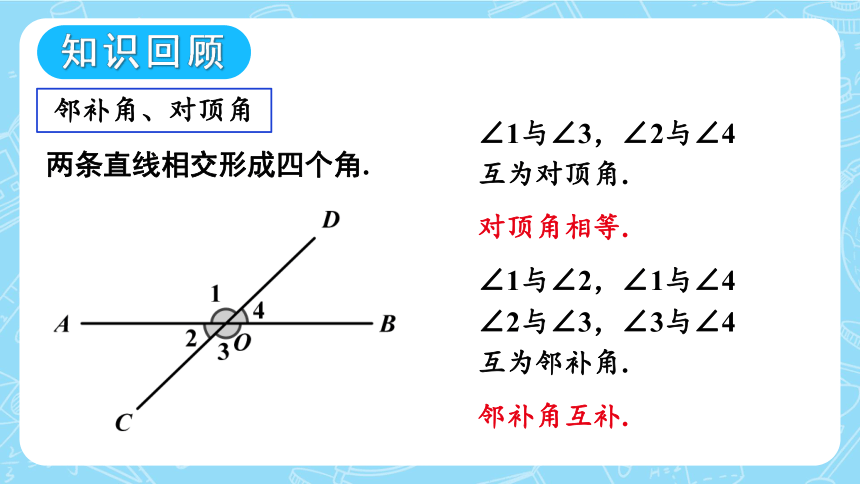
邻补角、对顶角
两条直线相交形成四个角.
∠1与∠3,∠2与∠4
互为对顶角.
对顶角相等.
∠1与∠2,∠1与∠4
∠2与∠3,∠3与∠4
互为邻补角.
邻补角互补.
知识回顾
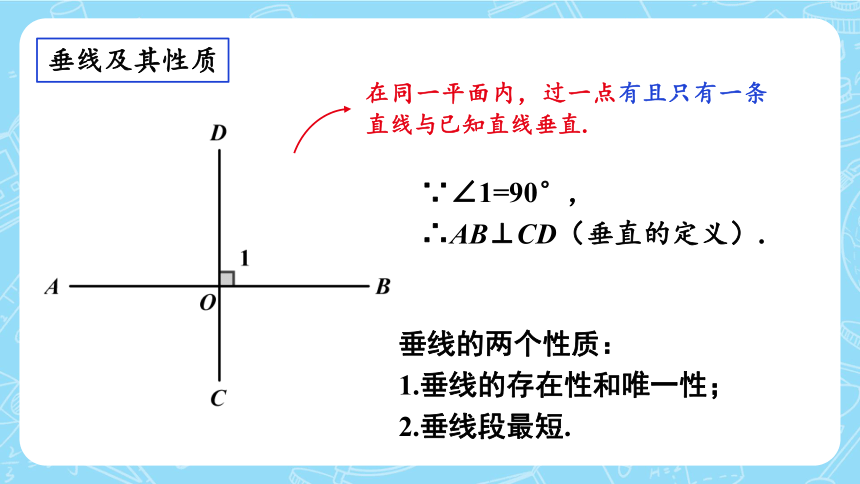
垂线及其性质
∵∠1=90°,
∴AB⊥CD(垂直的定义).
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的两个性质:
1.垂线的存在性和唯一性;
2.垂线段最短.
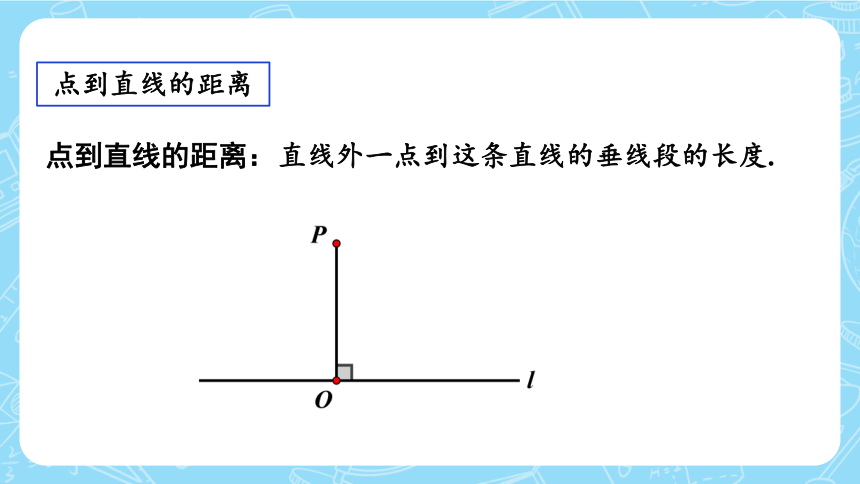
点到直线的距离
点到直线的距离:
直线外一点到这条直线的垂线段的长度.
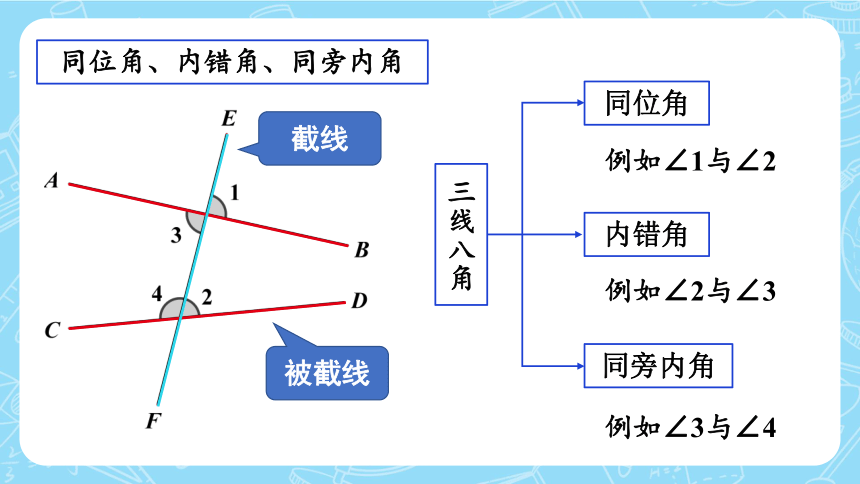
同位角、内错角、同旁内角
三线八角
同位角
内错角
同旁内角
被截线
截线
例如∠1与∠2
例如∠2与∠3
例如∠3与∠4
平行公理
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
即如果a‖b,a‖c,那么b‖c.
平行线的判定和性质
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
角的数量关系
直线的位置关系
角的数量关系
判定:证平行,用判定.
性质:知平行,用性质.
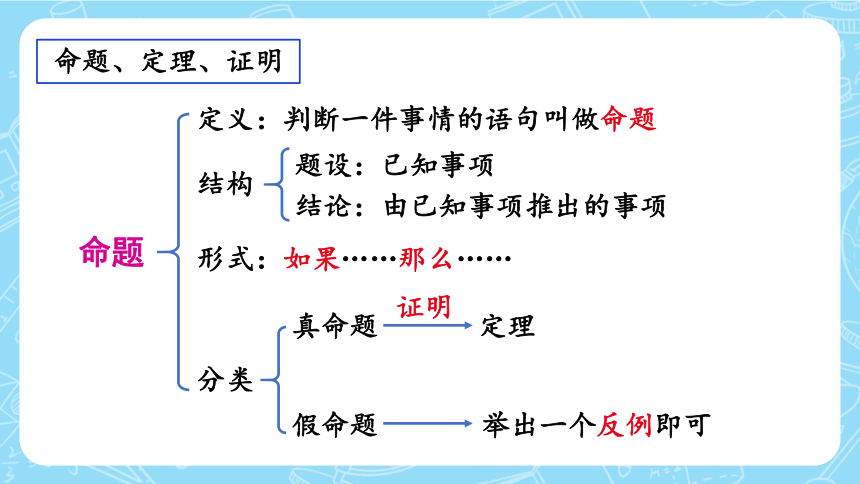
命题、定理、证明
命题
定义:判断一件事情的语句叫做命题
结构
题设:已知事项
结论:由已知事项推出的事项
形式:如果……那么……
分类
真命题
定理
证明
假命题
举出一个反例即可
平移
定义:把一个图形整体沿某一直线方向移动
两要素:平移的方向、平移的距离
作图:一定、二找、三移、四连、五写
平移前后图形的形状、大小完全相同
对应点所连的线段平行(或在同一条直线上)且相等
对应线段平行(或在同一条直线上)且相等,对应角相等
性质:
平移
1. 判断题(正确的画√,错误的画×).
(1)a,b,c 是直线,若 a∥b,b∥c,则a∥c; ( )
(2)a,b,c 是直线,若 a⊥b,b⊥c,则a⊥c. ( )
提示:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行.如果没有“在同一平面内”这个前提条件,则不一定平行,有可能垂直.
√
×
【选自教材第35页 复习题5 第1题】
复习巩固
2.如图,两条直线a,b相交.
(1)如果∠1=60°,求∠2,∠3,∠4的度数;
(2)如果 2∠3=3∠1,求∠2,∠3,∠4的度数.
解:(1)∠2=180°-∠1=180°-60°=120°(邻补角定义).
∠3=∠2=120°(对顶角相等).
∠4=∠1=60°(对顶角相等).
【选自教材第35页 复习题5 第2题】
2.如图,两条直线a,b相交.
(1)如果∠1=60°,求∠2,∠3,∠4的度数;
(2)如果 2∠3=3∠1,求∠2,∠3,∠4的度数.
(2)∵∠1+∠3=180°,
又2∠3=3∠1,即∠1= ∠3,
∴ ∠3+∠3 = 180°, ∠3 = 180°,
∠3=108°,∠2=∠3=108°(对顶角相等),
∠4=180°-∠3=180°-108°=72°(邻补角定义).
【选自教材第35页 复习题5 第2题】
3.如图,直线AB⊥CD,垂足为O,直线EF经过点O,∠1 =26°,求∠2,∠3,∠4的度数.
解:∵AB⊥CD,
∴∠COB=90°.
故∠2=90°-∠1=90°-26°=64°.
∵∠3与∠1是对顶角,
∴∠3=∠1=26°.
又∠4与∠1 是邻补角,
∴∠4=180°-∠1=180°-26°=154°.
【选自教材第35页 复习题5 第3题】
4. 根据下列语句画出图形:
(1)过线段AB的中点C,画CD⊥AB;
(2)点P到直线AB的距离是3cm,过点P画直线AB的垂线 PC;
(3)过三角形ABC内的一点P,分别画AB,BC,CA的平行线.
解:如图:
【选自教材第35页 复习题5 第4题】
5. 如图,某人骑自行车自A沿正东方向前进,至B处后,行驶方向改为东偏南 15°,行驶到C处仍按正东方向行驶,画出继续行驶的路线.
A
B
15°
解:如图所示:
【选自教材第36页 复习题5 第5题】
6.如图,∠1=30°,∠B=60°,AB⊥AC.
(1)∠DAB+∠B等于多少度?
(2)AD与BC平行吗?AB与CD平行吗?
【选自教材第36页 复习题5 第6题】
解:(1)∵AB⊥AC,∴∠2 = 90°.
则∠DAB+∠B=∠1+∠2+∠B=30°+90°+ 60°=180°.
(2)由(1)∠DAB +∠B=180°,得AD∥BC(同旁内角互补,两直线平行).
AB与CD不一定平行,如图中虚线所示.
2
7.如图,平行线a,b被直线c所截,知道∠1~∠8 中一个角的度数,能否求出其他角的度数?如果能,用其中一个角表示出其他各角.
【选自教材第36页 复习题5 第7题】
解:知道∠1~∠8中的一个角的度数,能求出其他角的度数,如用∠1表示其他各角. ∠2=180°-∠1,∠3=∠1,∠4=180°-∠1,∠5=∠1,∠6=180°-∠1,∠7=∠1,∠8=180°-∠1.
8.选择题.
(1)如图(1),点 E 在 AC 的延长线上,下列条件中能判断 AB∥CD 的是( ).
(A)∠3=∠4 (B)∠1=∠2
(C)∠D=∠DCE (D)∠D+∠ACD=180°
(1)
【选自教材第36页 复习题5 第8题】
B
综合运用
(2)如图(2),∠1 +∠2 = 180°,∠3 = 108°,则∠4 =( ).
(A)72° (B)80° (C)82° (D)108°
(2)
A
9.图中所示为一组护网的示意图,它可看成由两组平行线组成,你能通过检验一些角的大小来判断其中的线段是否平行吗?说出你的理由.
【选自教材第37页 复习题5 第9题】
解:可根据内错角相等,两直线平行,也可以利用同位角相等,两直线平行;同旁内角互补,两直线平行等来判断.
10. 如图,∠AOB内有一点P :
(1)过点P画出PC∥OB交OA于点C,画PD∥OA交OB于点 D;
(2)写出图中互补的角;
(3)写出图中相等的角.
【选自教材第37页 复习题5 第10题】
A
B
O
P
4
3
6
5
10
7
8
9
1
2
D
C
解:(1)如图所示.
(2) ∠1、∠O、∠6、∠4、∠8、∠10分别与∠2、∠3、∠5、∠7、∠9互补.
(3) ①∠1=∠O=∠6=∠4=∠8=∠10;
②∠2=∠3=∠5=∠7=∠9.
11.如图,利用平移可以画出一些立体图形.在方格纸上写出你的名字或你的校名,用类似的方法画出它的立体图.变换不同的长度和方向多试几次,你认为哪一种更具艺术效果?
【选自教材第37页 复习题5 第11题】
12.指出下列命题的题设和结论,并判断它们是真命题还是假命题.如果是假命题,举出一个反例.
(1)两个角的和等于平角时,这两个角互为补角;
(2)内错角相等;
(3)两条平行线被第三条直线所截,内错角相等.
【选自教材第37页 复习题5 第12题】
题设:如果两个角的和等于平角;结论:这两个角互为补角;是真命题.
题设:如果两个角是内错角;结论:这两个角相等;是假命题.
题设:如果两条平行线被第三条直线所截;结论:内错角相等;是真命题.
13.完成下面的证明.
(1)如图(1),点D,E,F分别是三角形ABC的边BC,CA,AB上的一点,DE∥BA,DF∥CA.求证∠FDE=∠A.
【选自教材第37页 复习题5 第13题】
(1)
证明:∵DE∥BA,
∴∠FDE=_______ (_______________________).
∵DF∥CA,
∴∠A=_______ (________________________).
∴∠FDE=∠A.
∠BFD
两直线平行,内错角相等
∠BFD
两直线平行,同位角相等
(2)如图(2),AB和CD相交于点O,∠C=∠COA,∠D =∠BOD.求证 AC∥BD .
(2)
证明:∵∠C =∠COA,∠D =∠BOD,
又∠COA =∠BOD (___________________),
∴∠C = ________.
∴AC∥BD (________________________).
对顶角相等
∠D
内错角相等,两直线平行
14. 如图,这是一套住房的平面图,图中有许多相交线和平行线.量量你家的住房,选择适当的比例尺,画出它的平面图.你能自己设计一个户型吗?
【选自教材第38页 复习题5 第14题】
拓广探索
15.一个台球桌的桌面如图所示,一个球在桌面上的点A滚向桌边PQ,碰着PQ上的点B后便反弹而滚向桌边RS,碰到RS上的点C便反弹而滚向点D. 如果PQ∥RS,AB,BC,CD都是直线,且∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,那么,球经过两次反弹后所滚的路径CD是否平行于原来的路径 AB?
A
S
P
B
N
M
C
D
Q
R
【选自教材第38页 复习题5 第15题】
解:如图所示:CD∥AB.理由如下:
∵QP∥RS,
∴∠1=∠6(两直线平行,内错角相等).
又 BN⊥QP,MC⊥RS,
∴∠1+∠3=90°,∠8+∠6=90°.
∴∠3=∠8(等角的余角相等).
由 BN⊥QP 可知∠1+∠3 =∠2+∠4=90°.
又由BN平分∠ABC,∴∠3=∠4.
同理可得∠7 =∠8.
∴∠3+∠4 = 2∠3,∠7+∠8 = 2∠8,
∴∠3+∠4 = ∠7+∠8.即∠CBA=∠DCB,
∴AB∥CD(内错角相等,两直线平行).
1.本章的核心知识有哪些?这些知识间有什么样的联系?
2.通过本节课的复习,谈谈你对本章的研究思路的体会以及如何研究图形的位置关系.
课堂小结
《练习册》主体部分相应课时训练.
课外作业
人教版·七年级下册
5
本章复习
相交线
两条直线相交
邻补角、对顶角
垂线及其性质
点到直线的距离
两条直线被第三条直线所截
同位角、内错角、同旁内角
平行线
平 移
平行公理
判定
性质
本章知识结构图
邻补角、对顶角
两条直线相交形成四个角.
∠1与∠3,∠2与∠4
互为对顶角.
对顶角相等.
∠1与∠2,∠1与∠4
∠2与∠3,∠3与∠4
互为邻补角.
邻补角互补.
知识回顾
垂线及其性质
∵∠1=90°,
∴AB⊥CD(垂直的定义).
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的两个性质:
1.垂线的存在性和唯一性;
2.垂线段最短.
点到直线的距离
点到直线的距离:
直线外一点到这条直线的垂线段的长度.
同位角、内错角、同旁内角
三线八角
同位角
内错角
同旁内角
被截线
截线
例如∠1与∠2
例如∠2与∠3
例如∠3与∠4
平行公理
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
即如果a‖b,a‖c,那么b‖c.
平行线的判定和性质
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
角的数量关系
直线的位置关系
角的数量关系
判定:证平行,用判定.
性质:知平行,用性质.
命题、定理、证明
命题
定义:判断一件事情的语句叫做命题
结构
题设:已知事项
结论:由已知事项推出的事项
形式:如果……那么……
分类
真命题
定理
证明
假命题
举出一个反例即可
平移
定义:把一个图形整体沿某一直线方向移动
两要素:平移的方向、平移的距离
作图:一定、二找、三移、四连、五写
平移前后图形的形状、大小完全相同
对应点所连的线段平行(或在同一条直线上)且相等
对应线段平行(或在同一条直线上)且相等,对应角相等
性质:
平移
1. 判断题(正确的画√,错误的画×).
(1)a,b,c 是直线,若 a∥b,b∥c,则a∥c; ( )
(2)a,b,c 是直线,若 a⊥b,b⊥c,则a⊥c. ( )
提示:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行.如果没有“在同一平面内”这个前提条件,则不一定平行,有可能垂直.
√
×
【选自教材第35页 复习题5 第1题】
复习巩固
2.如图,两条直线a,b相交.
(1)如果∠1=60°,求∠2,∠3,∠4的度数;
(2)如果 2∠3=3∠1,求∠2,∠3,∠4的度数.
解:(1)∠2=180°-∠1=180°-60°=120°(邻补角定义).
∠3=∠2=120°(对顶角相等).
∠4=∠1=60°(对顶角相等).
【选自教材第35页 复习题5 第2题】
2.如图,两条直线a,b相交.
(1)如果∠1=60°,求∠2,∠3,∠4的度数;
(2)如果 2∠3=3∠1,求∠2,∠3,∠4的度数.
(2)∵∠1+∠3=180°,
又2∠3=3∠1,即∠1= ∠3,
∴ ∠3+∠3 = 180°, ∠3 = 180°,
∠3=108°,∠2=∠3=108°(对顶角相等),
∠4=180°-∠3=180°-108°=72°(邻补角定义).
【选自教材第35页 复习题5 第2题】
3.如图,直线AB⊥CD,垂足为O,直线EF经过点O,∠1 =26°,求∠2,∠3,∠4的度数.
解:∵AB⊥CD,
∴∠COB=90°.
故∠2=90°-∠1=90°-26°=64°.
∵∠3与∠1是对顶角,
∴∠3=∠1=26°.
又∠4与∠1 是邻补角,
∴∠4=180°-∠1=180°-26°=154°.
【选自教材第35页 复习题5 第3题】
4. 根据下列语句画出图形:
(1)过线段AB的中点C,画CD⊥AB;
(2)点P到直线AB的距离是3cm,过点P画直线AB的垂线 PC;
(3)过三角形ABC内的一点P,分别画AB,BC,CA的平行线.
解:如图:
【选自教材第35页 复习题5 第4题】
5. 如图,某人骑自行车自A沿正东方向前进,至B处后,行驶方向改为东偏南 15°,行驶到C处仍按正东方向行驶,画出继续行驶的路线.
A
B
15°
解:如图所示:
【选自教材第36页 复习题5 第5题】
6.如图,∠1=30°,∠B=60°,AB⊥AC.
(1)∠DAB+∠B等于多少度?
(2)AD与BC平行吗?AB与CD平行吗?
【选自教材第36页 复习题5 第6题】
解:(1)∵AB⊥AC,∴∠2 = 90°.
则∠DAB+∠B=∠1+∠2+∠B=30°+90°+ 60°=180°.
(2)由(1)∠DAB +∠B=180°,得AD∥BC(同旁内角互补,两直线平行).
AB与CD不一定平行,如图中虚线所示.
2
7.如图,平行线a,b被直线c所截,知道∠1~∠8 中一个角的度数,能否求出其他角的度数?如果能,用其中一个角表示出其他各角.
【选自教材第36页 复习题5 第7题】
解:知道∠1~∠8中的一个角的度数,能求出其他角的度数,如用∠1表示其他各角. ∠2=180°-∠1,∠3=∠1,∠4=180°-∠1,∠5=∠1,∠6=180°-∠1,∠7=∠1,∠8=180°-∠1.
8.选择题.
(1)如图(1),点 E 在 AC 的延长线上,下列条件中能判断 AB∥CD 的是( ).
(A)∠3=∠4 (B)∠1=∠2
(C)∠D=∠DCE (D)∠D+∠ACD=180°
(1)
【选自教材第36页 复习题5 第8题】
B
综合运用
(2)如图(2),∠1 +∠2 = 180°,∠3 = 108°,则∠4 =( ).
(A)72° (B)80° (C)82° (D)108°
(2)
A
9.图中所示为一组护网的示意图,它可看成由两组平行线组成,你能通过检验一些角的大小来判断其中的线段是否平行吗?说出你的理由.
【选自教材第37页 复习题5 第9题】
解:可根据内错角相等,两直线平行,也可以利用同位角相等,两直线平行;同旁内角互补,两直线平行等来判断.
10. 如图,∠AOB内有一点P :
(1)过点P画出PC∥OB交OA于点C,画PD∥OA交OB于点 D;
(2)写出图中互补的角;
(3)写出图中相等的角.
【选自教材第37页 复习题5 第10题】
A
B
O
P
4
3
6
5
10
7
8
9
1
2
D
C
解:(1)如图所示.
(2) ∠1、∠O、∠6、∠4、∠8、∠10分别与∠2、∠3、∠5、∠7、∠9互补.
(3) ①∠1=∠O=∠6=∠4=∠8=∠10;
②∠2=∠3=∠5=∠7=∠9.
11.如图,利用平移可以画出一些立体图形.在方格纸上写出你的名字或你的校名,用类似的方法画出它的立体图.变换不同的长度和方向多试几次,你认为哪一种更具艺术效果?
【选自教材第37页 复习题5 第11题】
12.指出下列命题的题设和结论,并判断它们是真命题还是假命题.如果是假命题,举出一个反例.
(1)两个角的和等于平角时,这两个角互为补角;
(2)内错角相等;
(3)两条平行线被第三条直线所截,内错角相等.
【选自教材第37页 复习题5 第12题】
题设:如果两个角的和等于平角;结论:这两个角互为补角;是真命题.
题设:如果两个角是内错角;结论:这两个角相等;是假命题.
题设:如果两条平行线被第三条直线所截;结论:内错角相等;是真命题.
13.完成下面的证明.
(1)如图(1),点D,E,F分别是三角形ABC的边BC,CA,AB上的一点,DE∥BA,DF∥CA.求证∠FDE=∠A.
【选自教材第37页 复习题5 第13题】
(1)
证明:∵DE∥BA,
∴∠FDE=_______ (_______________________).
∵DF∥CA,
∴∠A=_______ (________________________).
∴∠FDE=∠A.
∠BFD
两直线平行,内错角相等
∠BFD
两直线平行,同位角相等
(2)如图(2),AB和CD相交于点O,∠C=∠COA,∠D =∠BOD.求证 AC∥BD .
(2)
证明:∵∠C =∠COA,∠D =∠BOD,
又∠COA =∠BOD (___________________),
∴∠C = ________.
∴AC∥BD (________________________).
对顶角相等
∠D
内错角相等,两直线平行
14. 如图,这是一套住房的平面图,图中有许多相交线和平行线.量量你家的住房,选择适当的比例尺,画出它的平面图.你能自己设计一个户型吗?
【选自教材第38页 复习题5 第14题】
拓广探索
15.一个台球桌的桌面如图所示,一个球在桌面上的点A滚向桌边PQ,碰着PQ上的点B后便反弹而滚向桌边RS,碰到RS上的点C便反弹而滚向点D. 如果PQ∥RS,AB,BC,CD都是直线,且∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,那么,球经过两次反弹后所滚的路径CD是否平行于原来的路径 AB?
A
S
P
B
N
M
C
D
Q
R
【选自教材第38页 复习题5 第15题】
解:如图所示:CD∥AB.理由如下:
∵QP∥RS,
∴∠1=∠6(两直线平行,内错角相等).
又 BN⊥QP,MC⊥RS,
∴∠1+∠3=90°,∠8+∠6=90°.
∴∠3=∠8(等角的余角相等).
由 BN⊥QP 可知∠1+∠3 =∠2+∠4=90°.
又由BN平分∠ABC,∴∠3=∠4.
同理可得∠7 =∠8.
∴∠3+∠4 = 2∠3,∠7+∠8 = 2∠8,
∴∠3+∠4 = ∠7+∠8.即∠CBA=∠DCB,
∴AB∥CD(内错角相等,两直线平行).
1.本章的核心知识有哪些?这些知识间有什么样的联系?
2.通过本节课的复习,谈谈你对本章的研究思路的体会以及如何研究图形的位置关系.
课堂小结
《练习册》主体部分相应课时训练.
课外作业
