最新人教版七下数学 第五章 相交线与平行线 数学活动(21张PPT)
文档属性
| 名称 | 最新人教版七下数学 第五章 相交线与平行线 数学活动(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 08:22:34 | ||
图片预览





文档简介
(共21张PPT)
相交线与平行线
数学活动
5
复习回顾
思考:怎样过一点画一条已知直线的平行线?
l
P
一放;
二靠;
三移;
四画.
同学们知道有哪些判定两条直线平行的方法呢?
用角的数量关系来判定:
1.同位角相等,两直线行;
2.内错角相等,两直线行;
3.同旁内角互补,两直线行.
用直线的位置关系来判定:
1.平行公理的推论:平行于同一条直线的两条直线平行;
2.在同一平面内,垂直于同一条直线的两条直线平行.
探索新知
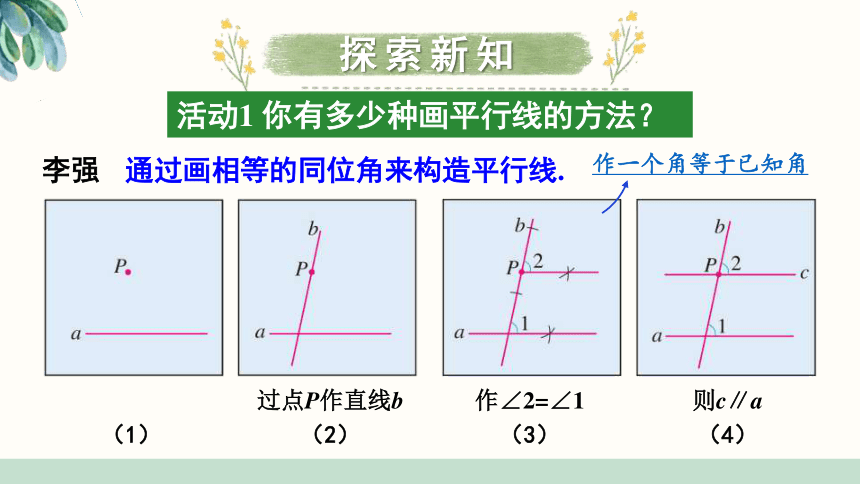
活动1 你有多少种画平行线的方法?
过点P作直线b
则c∥a
作∠2=∠1
李强
(1)
(2)
(3)
(4)
通过画相等的同位角来构造平行线.
作一个角等于已知角
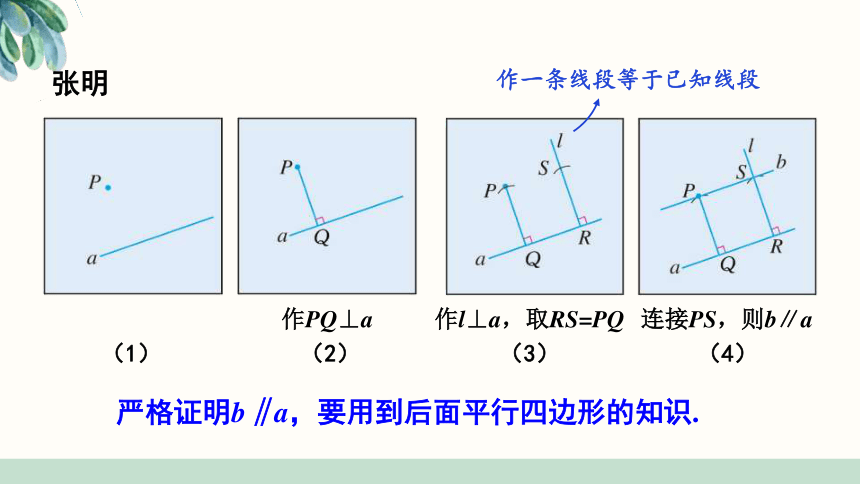
作PQ⊥a
连接PS,则b∥a
作l⊥a,取RS=PQ
(1)
(2)
(3)
(4)
张明
作一条线段等于已知线段
严格证明b‖a,要用到后面平行四边形的知识.
a
P
a
P
b
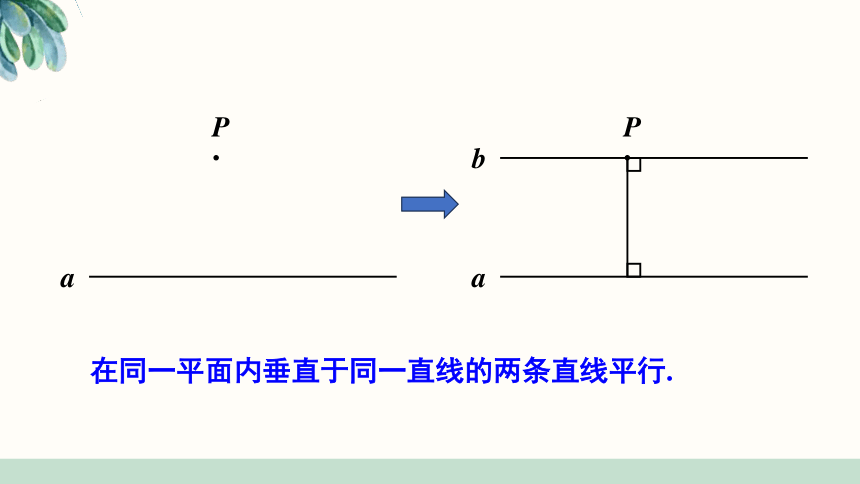
在同一平面内垂直于同一直线的两条直线平行.
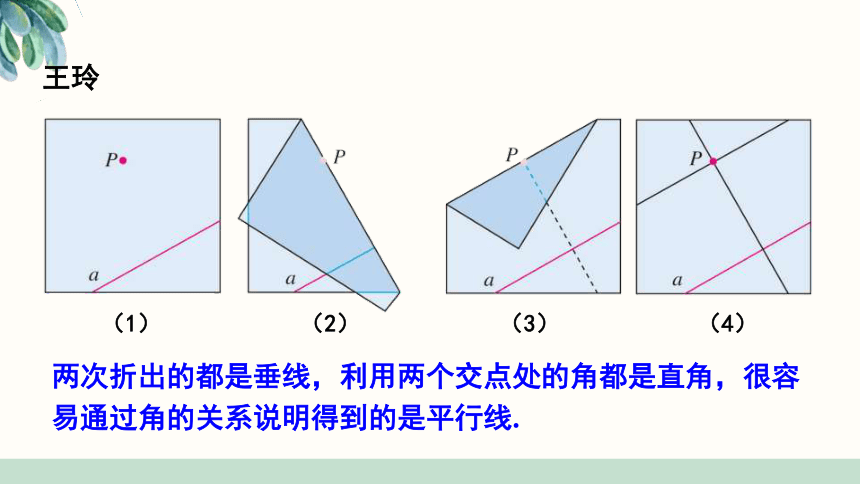
王玲
(1)
(2)
(3)
(4)
两次折出的都是垂线,利用两个交点处的角都是直角,很容易通过角的关系说明得到的是平行线.
AB两点均在格点上,你能过点D做出AB的平行线吗?
活动2 设计美丽的图案
利用平移,可以设计非常美丽的图案,例如:
图中每一匹马都可以由正方形上的平移得到.
类似地,你还能用平移设计一些图案吗?
随堂练习
1.继续探究最后画出的这个图形,若∠ABP=150°,试求∠PDE的度数.
P
B
A
D
E
G
F
要求∠PDE的度数
同位角、内错角、同旁内角
转化
P
B
A
D
E
G
F
解:由正方形纸片可知,AB//DE,过点P作FG//DE.
∴∠1=∠PDE(两直线平行,内错角相等).
∵AB//DE.
∴AB//FG(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠2=∠ABP(两直线平行,内错角相等).
∵∠ABP=150°,
∴∠2=150°(等量代换)
∵∠1+∠2+∠BPD=360°,∠BPD=90°,
∴∠1=360°-∠2-∠BPD=120°.
∴∠PDE=120°.
1
2
解:∵∠1+∠2=180°,且∠1+∠EFD=180°,
∴∠2=∠EFD.
又∵∠DEF=∠A,
且∠EDF=180°-∠DEF-∠EFD,
∠ACD=180°-∠A-∠2,
∴∠ACD=∠EDF.
∴DE∥AC(内错角相等,两直线平行).
∴∠ACB=∠BED=60°(两直线平行,同位角相等).
2.如图,已知∠1+∠2=180°,∠DEF=∠A,∠BED=60°,求∠ACB的度数.
回顾整个活动过程,反思自己有哪些收获(掌握了平行线的哪些画法和判定方法)和不足.
课堂小结
《练习册》主体部分相应课时训练.
课后作业
相交线与平行线
数学活动
5
复习回顾
思考:怎样过一点画一条已知直线的平行线?
l
P
一放;
二靠;
三移;
四画.
同学们知道有哪些判定两条直线平行的方法呢?
用角的数量关系来判定:
1.同位角相等,两直线行;
2.内错角相等,两直线行;
3.同旁内角互补,两直线行.
用直线的位置关系来判定:
1.平行公理的推论:平行于同一条直线的两条直线平行;
2.在同一平面内,垂直于同一条直线的两条直线平行.
探索新知
活动1 你有多少种画平行线的方法?
过点P作直线b
则c∥a
作∠2=∠1
李强
(1)
(2)
(3)
(4)
通过画相等的同位角来构造平行线.
作一个角等于已知角
作PQ⊥a
连接PS,则b∥a
作l⊥a,取RS=PQ
(1)
(2)
(3)
(4)
张明
作一条线段等于已知线段
严格证明b‖a,要用到后面平行四边形的知识.
a
P
a
P
b
在同一平面内垂直于同一直线的两条直线平行.
王玲
(1)
(2)
(3)
(4)
两次折出的都是垂线,利用两个交点处的角都是直角,很容易通过角的关系说明得到的是平行线.
AB两点均在格点上,你能过点D做出AB的平行线吗?
活动2 设计美丽的图案
利用平移,可以设计非常美丽的图案,例如:
图中每一匹马都可以由正方形上的平移得到.
类似地,你还能用平移设计一些图案吗?
随堂练习
1.继续探究最后画出的这个图形,若∠ABP=150°,试求∠PDE的度数.
P
B
A
D
E
G
F
要求∠PDE的度数
同位角、内错角、同旁内角
转化
P
B
A
D
E
G
F
解:由正方形纸片可知,AB//DE,过点P作FG//DE.
∴∠1=∠PDE(两直线平行,内错角相等).
∵AB//DE.
∴AB//FG(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠2=∠ABP(两直线平行,内错角相等).
∵∠ABP=150°,
∴∠2=150°(等量代换)
∵∠1+∠2+∠BPD=360°,∠BPD=90°,
∴∠1=360°-∠2-∠BPD=120°.
∴∠PDE=120°.
1
2
解:∵∠1+∠2=180°,且∠1+∠EFD=180°,
∴∠2=∠EFD.
又∵∠DEF=∠A,
且∠EDF=180°-∠DEF-∠EFD,
∠ACD=180°-∠A-∠2,
∴∠ACD=∠EDF.
∴DE∥AC(内错角相等,两直线平行).
∴∠ACB=∠BED=60°(两直线平行,同位角相等).
2.如图,已知∠1+∠2=180°,∠DEF=∠A,∠BED=60°,求∠ACB的度数.
回顾整个活动过程,反思自己有哪些收获(掌握了平行线的哪些画法和判定方法)和不足.
课堂小结
《练习册》主体部分相应课时训练.
课后作业
