鲁教版(五四制)七年级数学下册第十一章一元一次不等式与不等式组综合测评试卷(含答案详解)
文档属性
| 名称 | 鲁教版(五四制)七年级数学下册第十一章一元一次不等式与不等式组综合测评试卷(含答案详解) |  | |
| 格式 | docx | ||
| 文件大小 | 287.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 08:25:34 | ||
图片预览




文档简介
七年级数学下册第十一章一元一次不等式与不等式组综合测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,若点A表示数为.则( )
A. B. C. D.
2、检测游泳池的水质,要求三次检验的pH的平均值不小于7.2,且不大于7.8.前两次检验,pH的读数分别是7.4,7.9,那么第三次检验的pH应该为多少才能合格?设第3次的pH值为x,由题意可得( )
A. B.
C. D.
3、已知关于x、y的二元一次方程组的解满足,且关于s的不等式组恰好有4个整数解,那么所有符合条件的整数a的个数为( )
A.4个 B.3个 C.2个 D.1个
4、若,那么下列各式中正确的是( )
A. B.
C. D.
5、如图,函数和的图像相交于点P(1,m),则不等式的解集为( )
A. B. C. D.
6、已知,那么下列各式中,不一定成立的是( )
A. B. C. D.
7、下列式子中,是一元一次不等式的有( )
①3a-2=4a+9;②3x-6>3y+7;③2x3<5;④x2>1;⑤2x+6>x.
A.1个 B.2个 C.3个 D.4个
8、下列数值“-2,0,1,2,4”中是不等式的解的有( )个.
A.4 B.3 C.2 D.1
9、若,则不等式组的解集是( )
A. B. C. D.无解
10、不等式组的最小整数解是( )
A.5 B.0 C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、判断下列不等式组是否为一元一次不等式组:
(1)__________;(2)__________;
(3) __________;(4)__________
2、①-2<0;②2x>3;③2≠3;④2x2-1;⑤x≠-5中是不等式的有____(填序号).
3、如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组的解是________;当ax+b≤kx时,x的取值范围是____________.
4、不等式2x﹣3<4x的最小整数解是____.
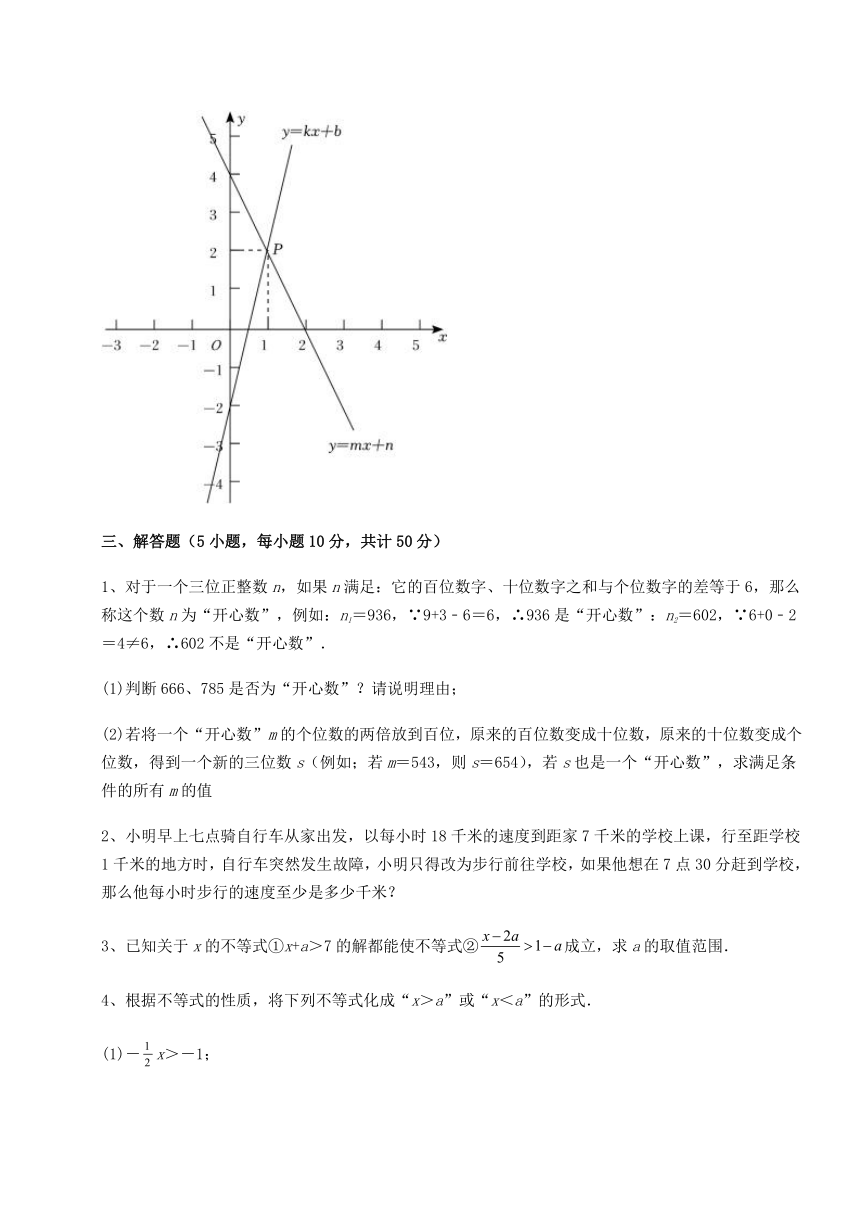
5、如图,一次函数和的图象交于点,则不等式的解集是______.
三、解答题(5小题,每小题10分,共计50分)
1、对于一个三位正整数n,如果n满足:它的百位数字、十位数字之和与个位数字的差等于6,那么称这个数n为“开心数”,例如:n1=936,∵9+3﹣6=6,∴936是“开心数”:n2=602,∵6+0﹣2=4≠6,∴602不是“开心数”.
(1)判断666、785是否为“开心数”?请说明理由;
(2)若将一个“开心数”m的个位数的两倍放到百位,原来的百位数变成十位数,原来的十位数变成个位数,得到一个新的三位数s(例如;若m=543,则s=654),若s也是一个“开心数”,求满足条件的所有m的值
2、小明早上七点骑自行车从家出发,以每小时18千米的速度到距家7千米的学校上课,行至距学校1千米的地方时,自行车突然发生故障,小明只得改为步行前往学校,如果他想在7点30分赶到学校,那么他每小时步行的速度至少是多少千米?
3、已知关于x的不等式①x+a>7的解都能使不等式②成立,求a的取值范围.
4、根据不等式的性质,将下列不等式化成“x>a”或“x<a”的形式.
(1)-x>-1;
(2)x>x﹣6.
5、已知一次函数y1=ax+b,y2=bx+a(ab≠0,且a≠b).
(1)若y1过点(1,2)与点(2,b﹣a﹣3)求y1的函数表达式;
(2)y1与y2的图象交于点A(m,n),用含a,b的代数式表示n;
(3)设y3=y1﹣y2,y4=y2﹣y1,当y3>y4时,求x的取值范围.
-参考答案-
一、单选题
1、D
【解析】
【分析】
根据点A在数轴上的位置可得出关于x的一元一次不等式组,解之即可求解.
【详解】
解:由数轴可知,1<x+1<2,
∴0<x<1,
故选:D.
【点睛】
本题考查数轴、解一元一次不等式组,能从数轴上得出关于x的一元一次不等式组是解答的关键.
2、A
【解析】
【分析】
根据平均数的定义,并结合三次检验的pH的平均值不小于7.2,且不大于7.8可得7.2≤≤7.8,从而得出答案.
【详解】
解:根据题意知7.2≤≤7.8,
∴7.2×3≤7.4+7.9+x≤7.8×3,
故选:A.
【点睛】
本题主要考查由实际问题抽象出一元一次不等式组,解题的关键是掌握平均数的定义.
3、C
【解析】
【分析】
先求出方程组和不等式的解集,再求出a的范围,最后得出答案即可.
【详解】
解:解方程组得:,
∵关于x、y的二元一次方程组的解满足,
∴≥,
解得:a≥-,
∵关于s的不等式组恰好有4个整数解,即4个整数解为1,0,-1,-2,
∴,
解得-2≤a<1,
∴≤a<1,
∴符合条件的整数a的值有:-1,0,共2个,
故选:C.
【点睛】
本题主要考查了解二元一次方程和一元一次不等式组的整数解,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
4、C
【解析】
【分析】
根据不等式的性质判断.
【详解】
解:∵,∴a+1>b+1,故选项A错误;
∵,∴-a<-b,故选项B错误;
∵,∴,故选项C正确;
∵,∴,故选项D错误;
故选:C.
【点睛】
此题考查了不等式的性质,熟记不等式的性质是解题的关键.
5、B
【解析】
【分析】
由题意首先确定y=mx和y=kx-b的交点以及作出y=kx-b的大体图象,进而根据图象进行判断即可.
【详解】
解:∵y=kx+b的图象经过点P(1,m),
∴k+b=m,
当x=-1时,kx-b=-k-b=-(k+b)=-m,
即(-1,-m)在函数y=kx-b的图象上.
又∵(-1,-m)在y=mx的图象上.
∴y=kx-b与y=mx相交于点(-1,-m).
则函数图象如图.
则不等式-b≤kx-b≤mx的解集为-1≤x≤0.
故选:B.
【点睛】
本题考查一次函数与不等式的关系,运用数形结合思维分析并正确确定y=kx-b和y=mx的交点是解题的关键.
6、A
【解析】
【分析】
根据不等式的性质1不等式不等式两边同时加或减去同一个数或整式,不等号方向不变,基本性质2:不等式两边同时乘以(或除以)同一个大于0的整数,不等号方向不变 基本性质3:不等式两边同时乘以(或除以)同一个小于0的整数,不等号方向改变,根据不等式性质对各选项进行一一分析判断即可.
【详解】
解:.,不妨设,
则,
选项符合题意;
B.,
,
选项B不符合题意;
C.,
,
,
选项C不符合题意;
D.,
,
,
选项D不符合题意;
故选:A.
【点睛】
本题考查不等式性质,掌握不等式性质是解题关键.
7、A
【解析】
【分析】
根据一元一次不等式的定义逐个判断即可.
【详解】
解:①3a-2=4a+9是方程;②3x-6>3y+7中有两个未知数;③2x3<5未知数的次数不是一次;④x2>1未知数的次数不是一次;⑤2x+6>x是一元一次不等式;
故选:A.
【点睛】
本题考查了一元一次不等式的定义,注意:只含有一个未知数,并且所含未知数的项的最高次数是1,并且不等式的两边都是整式的不等式叫一元一次不等式.
8、C
【解析】
【分析】
求出不等式的解集再进行判断即可.
【详解】
解:解,得
在-2,0,1,2,4中符合条件的有2和4共2个,
故选:C
【点睛】
本题考查了不等式的解集.解答此题关键是根据不等式的解集与各选项相比较看是否相符.
9、D
【解析】
【分析】
根据求不等式组的解集方法:“大大小小找不到”判断即可”
【详解】
若,则不等式组的解集是无解.
故选:D.
【点睛】
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
10、C
【解析】
【分析】
分别求出各不等式的解集,再求出其公共解集,然后求出最小整数解即可.
【详解】
解:解不等式,得:,
解不等式,得:,
故不等式组的解集为:,
则该不等式组的最小整数解为:.
故选:C.
【点睛】
本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
二、填空题
1、 不是 是 不是 是
【解析】
略
2、①②③⑤
【解析】
【分析】
根据不等式的定义用“>”、“≥”、“<”、“≤”、“≠”等不等号表示不相等关系的式子是不等式,依次判断5个式子即可.
【详解】
解:依据不等式的定义用不等号连接表示不相等关系的式子是不等式,分析可得这5个式子中,①②③⑤是不等式,④是代数式;
故答案为:①②③⑤.
【点睛】
本题属基本概念型的题目,考查不等式的定义,注意x≠-5这个式子,难度不大.
3、 x ≥-4
【解析】
【分析】
根据图像可知,函数和交于点P(-4,-2),即可得二元一次方程组的解;根据函数图像可知,当时,.
【详解】
解:根据图像可知,函数和交于点P(-4,-2),
则二元一次方程组的解是,
由图像可知,当时,,
故答案为:;.
【点睛】
本题考查了一次函数与二元一次方程组,解题的关键是掌握一次函数的性质.
4、
【解析】
【详解】
解:,
,
,
最小整数解是,
故答案为.
【点睛】
本题考查了一元一次不等式的整数解,解题的关键是求出不等式的解集.
5、x≥1
【解析】
【分析】
结合图象,写出直线y=mx+n在直线y=kx+b下方所对应的自变量的范围即可.
【详解】
解:∵函数y=mx+n的图象与y=kx+b的图象交于点P(1,2),
∴当x≥1时,kx+b≥mx+n,
∴不等式的解集为x≥1.
故答案为:x≥1.
【点睛】
本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
三、解答题
1、 (1)666是“开心数”,785不是“开心数”,理由见解析
(2)464和532
【解析】
【分析】
(1)根据“开心数”的定义即可得;
(2)设的百位数字为,十位数字为,个位数字为,从而可得的百位数字为,十位数字为,个位数字为,再根据“开心数”的定义列出等式,将都用表示出来,然后根据求出的取值范围,最后根据为正整数进行分析即可得.
(1)
解:666是“开心数”,785不是“开心数”,理由如下:
,
是“开心数”,
,
不是“开心数”.
(2)
解:设的百位数字为,十位数字为,个位数字为,
则的百位数字为,十位数字为,个位数字为,
和都是“开心数”,
,
解得,,
,
,
解得,
又为正整数,
所有符合条件的取值为,
当时,,则,
当时,,则,
2、小明每小时步行的速度至少是6千米.
【解析】
【分析】
设小明步行的速度为x千米/时,利用路程=速度×时间,结合小明想在7点30分之前赶到学校,即可得出关于x的一元一次不等式,解之取其中的最小值即可得出结论.
【详解】
解:设小明步行的速度为x千米/时,
依题意得:(7-1)+(-)x≥7,
解得:x≥6.
答:每小时步行的速度至少是6千米.
【点睛】
本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
3、
【解析】
【分析】
先求出不等式①②的解集,然后根据关于x的不等式①的解都能使不等式②成立得出,求解即可得.
【详解】
解:解不等式①得:,
解不等式②得:,
∵关于x的不等式①的解都能使不等式②成立,
∴,
解得:.
【点睛】
题目主要考查求不等式的解集,理解题意,熟练掌握解不等式的方法是解题关键.
4、 (1)x<2
(2)x>﹣12
【解析】
【分析】
(1)不等式两边都乘以-2即可得到解集;
(2)不等式的两边同时减去x,再乘以2即可求出解集.
(1)
解:-x>-1,
两边都乘以-2,得x<2.
(2)
解:原不等式的两边同时减去x,得
x>﹣6,
不等式的两边同时乘以2,得
x>﹣12.
【点睛】
此题考查了解一元一次不等式,正确掌握解不等式的步骤及方法是解题的关键.
5、 (1)y1=﹣x+3
(2)n=a+b
(3)当a>b时,x>1;当a<b时,x<1
【解析】
【分析】
(1)把(1,2)、(2,b-a-3)分别代入y1=ax+b得到a、b的方程组,然后解方程组得到y1的函数表达式;
(2)把A(m,n)分别代入y1=ax+b和y2=bx+a中得到,先利用加减消元法求出m,然后得到n与a、b的关系式;
(3)先用a、b表示y3和y4,利用y3>y4得到(a-b)x+b-a>(b-a)x+a-b,然后解不等式即可.
(1)
解:把(1,2)、(2,b﹣a﹣3)分别代入y1=ax+b得
,
解得,
∴y1的函数表达式为y1=﹣x+3;
(2)
解:∵y1与y2的图象交于点A(m,n),
∴,
∴m=1,n=a+b;
(3)
解:y3=y1﹣y2=ax+b﹣(bx+a)=(a﹣b)x+b﹣a,
y4=y2﹣y1=bx+a﹣(ax+b)=(b﹣a)x+a﹣b,
∵y3>y4,
∴(a﹣b)x+b﹣a>(b﹣a)x+a﹣b,
整理得(a﹣b)x>a﹣b,
当a>b时,x>1;
当a<b时,x<1.
【点睛】
本题考查了待定系数法求一次函数解析式:设一次函数解析式为y=kx+b(k≠0),再把两组对应量代入,然后解关于k,b的二元一次方程组.从而得到一次函数解析式.也考查了一次函数的性质.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,若点A表示数为.则( )
A. B. C. D.
2、检测游泳池的水质,要求三次检验的pH的平均值不小于7.2,且不大于7.8.前两次检验,pH的读数分别是7.4,7.9,那么第三次检验的pH应该为多少才能合格?设第3次的pH值为x,由题意可得( )
A. B.
C. D.
3、已知关于x、y的二元一次方程组的解满足,且关于s的不等式组恰好有4个整数解,那么所有符合条件的整数a的个数为( )
A.4个 B.3个 C.2个 D.1个
4、若,那么下列各式中正确的是( )
A. B.
C. D.
5、如图,函数和的图像相交于点P(1,m),则不等式的解集为( )
A. B. C. D.
6、已知,那么下列各式中,不一定成立的是( )
A. B. C. D.
7、下列式子中,是一元一次不等式的有( )
①3a-2=4a+9;②3x-6>3y+7;③2x3<5;④x2>1;⑤2x+6>x.
A.1个 B.2个 C.3个 D.4个
8、下列数值“-2,0,1,2,4”中是不等式的解的有( )个.
A.4 B.3 C.2 D.1
9、若,则不等式组的解集是( )
A. B. C. D.无解
10、不等式组的最小整数解是( )
A.5 B.0 C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、判断下列不等式组是否为一元一次不等式组:
(1)__________;(2)__________;
(3) __________;(4)__________
2、①-2<0;②2x>3;③2≠3;④2x2-1;⑤x≠-5中是不等式的有____(填序号).
3、如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组的解是________;当ax+b≤kx时,x的取值范围是____________.
4、不等式2x﹣3<4x的最小整数解是____.
5、如图,一次函数和的图象交于点,则不等式的解集是______.
三、解答题(5小题,每小题10分,共计50分)
1、对于一个三位正整数n,如果n满足:它的百位数字、十位数字之和与个位数字的差等于6,那么称这个数n为“开心数”,例如:n1=936,∵9+3﹣6=6,∴936是“开心数”:n2=602,∵6+0﹣2=4≠6,∴602不是“开心数”.
(1)判断666、785是否为“开心数”?请说明理由;
(2)若将一个“开心数”m的个位数的两倍放到百位,原来的百位数变成十位数,原来的十位数变成个位数,得到一个新的三位数s(例如;若m=543,则s=654),若s也是一个“开心数”,求满足条件的所有m的值
2、小明早上七点骑自行车从家出发,以每小时18千米的速度到距家7千米的学校上课,行至距学校1千米的地方时,自行车突然发生故障,小明只得改为步行前往学校,如果他想在7点30分赶到学校,那么他每小时步行的速度至少是多少千米?
3、已知关于x的不等式①x+a>7的解都能使不等式②成立,求a的取值范围.
4、根据不等式的性质,将下列不等式化成“x>a”或“x<a”的形式.
(1)-x>-1;
(2)x>x﹣6.
5、已知一次函数y1=ax+b,y2=bx+a(ab≠0,且a≠b).
(1)若y1过点(1,2)与点(2,b﹣a﹣3)求y1的函数表达式;
(2)y1与y2的图象交于点A(m,n),用含a,b的代数式表示n;
(3)设y3=y1﹣y2,y4=y2﹣y1,当y3>y4时,求x的取值范围.
-参考答案-
一、单选题
1、D
【解析】
【分析】
根据点A在数轴上的位置可得出关于x的一元一次不等式组,解之即可求解.
【详解】
解:由数轴可知,1<x+1<2,
∴0<x<1,
故选:D.
【点睛】
本题考查数轴、解一元一次不等式组,能从数轴上得出关于x的一元一次不等式组是解答的关键.
2、A
【解析】
【分析】
根据平均数的定义,并结合三次检验的pH的平均值不小于7.2,且不大于7.8可得7.2≤≤7.8,从而得出答案.
【详解】
解:根据题意知7.2≤≤7.8,
∴7.2×3≤7.4+7.9+x≤7.8×3,
故选:A.
【点睛】
本题主要考查由实际问题抽象出一元一次不等式组,解题的关键是掌握平均数的定义.
3、C
【解析】
【分析】
先求出方程组和不等式的解集,再求出a的范围,最后得出答案即可.
【详解】
解:解方程组得:,
∵关于x、y的二元一次方程组的解满足,
∴≥,
解得:a≥-,
∵关于s的不等式组恰好有4个整数解,即4个整数解为1,0,-1,-2,
∴,
解得-2≤a<1,
∴≤a<1,
∴符合条件的整数a的值有:-1,0,共2个,
故选:C.
【点睛】
本题主要考查了解二元一次方程和一元一次不等式组的整数解,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
4、C
【解析】
【分析】
根据不等式的性质判断.
【详解】
解:∵,∴a+1>b+1,故选项A错误;
∵,∴-a<-b,故选项B错误;
∵,∴,故选项C正确;
∵,∴,故选项D错误;
故选:C.
【点睛】
此题考查了不等式的性质,熟记不等式的性质是解题的关键.
5、B
【解析】
【分析】
由题意首先确定y=mx和y=kx-b的交点以及作出y=kx-b的大体图象,进而根据图象进行判断即可.
【详解】
解:∵y=kx+b的图象经过点P(1,m),
∴k+b=m,
当x=-1时,kx-b=-k-b=-(k+b)=-m,
即(-1,-m)在函数y=kx-b的图象上.
又∵(-1,-m)在y=mx的图象上.
∴y=kx-b与y=mx相交于点(-1,-m).
则函数图象如图.
则不等式-b≤kx-b≤mx的解集为-1≤x≤0.
故选:B.
【点睛】
本题考查一次函数与不等式的关系,运用数形结合思维分析并正确确定y=kx-b和y=mx的交点是解题的关键.
6、A
【解析】
【分析】
根据不等式的性质1不等式不等式两边同时加或减去同一个数或整式,不等号方向不变,基本性质2:不等式两边同时乘以(或除以)同一个大于0的整数,不等号方向不变 基本性质3:不等式两边同时乘以(或除以)同一个小于0的整数,不等号方向改变,根据不等式性质对各选项进行一一分析判断即可.
【详解】
解:.,不妨设,
则,
选项符合题意;
B.,
,
选项B不符合题意;
C.,
,
,
选项C不符合题意;
D.,
,
,
选项D不符合题意;
故选:A.
【点睛】
本题考查不等式性质,掌握不等式性质是解题关键.
7、A
【解析】
【分析】
根据一元一次不等式的定义逐个判断即可.
【详解】
解:①3a-2=4a+9是方程;②3x-6>3y+7中有两个未知数;③2x3<5未知数的次数不是一次;④x2>1未知数的次数不是一次;⑤2x+6>x是一元一次不等式;
故选:A.
【点睛】
本题考查了一元一次不等式的定义,注意:只含有一个未知数,并且所含未知数的项的最高次数是1,并且不等式的两边都是整式的不等式叫一元一次不等式.
8、C
【解析】
【分析】
求出不等式的解集再进行判断即可.
【详解】
解:解,得
在-2,0,1,2,4中符合条件的有2和4共2个,
故选:C
【点睛】
本题考查了不等式的解集.解答此题关键是根据不等式的解集与各选项相比较看是否相符.
9、D
【解析】
【分析】
根据求不等式组的解集方法:“大大小小找不到”判断即可”
【详解】
若,则不等式组的解集是无解.
故选:D.
【点睛】
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
10、C
【解析】
【分析】
分别求出各不等式的解集,再求出其公共解集,然后求出最小整数解即可.
【详解】
解:解不等式,得:,
解不等式,得:,
故不等式组的解集为:,
则该不等式组的最小整数解为:.
故选:C.
【点睛】
本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
二、填空题
1、 不是 是 不是 是
【解析】
略
2、①②③⑤
【解析】
【分析】
根据不等式的定义用“>”、“≥”、“<”、“≤”、“≠”等不等号表示不相等关系的式子是不等式,依次判断5个式子即可.
【详解】
解:依据不等式的定义用不等号连接表示不相等关系的式子是不等式,分析可得这5个式子中,①②③⑤是不等式,④是代数式;
故答案为:①②③⑤.
【点睛】
本题属基本概念型的题目,考查不等式的定义,注意x≠-5这个式子,难度不大.
3、 x ≥-4
【解析】
【分析】
根据图像可知,函数和交于点P(-4,-2),即可得二元一次方程组的解;根据函数图像可知,当时,.
【详解】
解:根据图像可知,函数和交于点P(-4,-2),
则二元一次方程组的解是,
由图像可知,当时,,
故答案为:;.
【点睛】
本题考查了一次函数与二元一次方程组,解题的关键是掌握一次函数的性质.
4、
【解析】
【详解】
解:,
,
,
最小整数解是,
故答案为.
【点睛】
本题考查了一元一次不等式的整数解,解题的关键是求出不等式的解集.
5、x≥1
【解析】
【分析】
结合图象,写出直线y=mx+n在直线y=kx+b下方所对应的自变量的范围即可.
【详解】
解:∵函数y=mx+n的图象与y=kx+b的图象交于点P(1,2),
∴当x≥1时,kx+b≥mx+n,
∴不等式的解集为x≥1.
故答案为:x≥1.
【点睛】
本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
三、解答题
1、 (1)666是“开心数”,785不是“开心数”,理由见解析
(2)464和532
【解析】
【分析】
(1)根据“开心数”的定义即可得;
(2)设的百位数字为,十位数字为,个位数字为,从而可得的百位数字为,十位数字为,个位数字为,再根据“开心数”的定义列出等式,将都用表示出来,然后根据求出的取值范围,最后根据为正整数进行分析即可得.
(1)
解:666是“开心数”,785不是“开心数”,理由如下:
,
是“开心数”,
,
不是“开心数”.
(2)
解:设的百位数字为,十位数字为,个位数字为,
则的百位数字为,十位数字为,个位数字为,
和都是“开心数”,
,
解得,,
,
,
解得,
又为正整数,
所有符合条件的取值为,
当时,,则,
当时,,则,
2、小明每小时步行的速度至少是6千米.
【解析】
【分析】
设小明步行的速度为x千米/时,利用路程=速度×时间,结合小明想在7点30分之前赶到学校,即可得出关于x的一元一次不等式,解之取其中的最小值即可得出结论.
【详解】
解:设小明步行的速度为x千米/时,
依题意得:(7-1)+(-)x≥7,
解得:x≥6.
答:每小时步行的速度至少是6千米.
【点睛】
本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
3、
【解析】
【分析】
先求出不等式①②的解集,然后根据关于x的不等式①的解都能使不等式②成立得出,求解即可得.
【详解】
解:解不等式①得:,
解不等式②得:,
∵关于x的不等式①的解都能使不等式②成立,
∴,
解得:.
【点睛】
题目主要考查求不等式的解集,理解题意,熟练掌握解不等式的方法是解题关键.
4、 (1)x<2
(2)x>﹣12
【解析】
【分析】
(1)不等式两边都乘以-2即可得到解集;
(2)不等式的两边同时减去x,再乘以2即可求出解集.
(1)
解:-x>-1,
两边都乘以-2,得x<2.
(2)
解:原不等式的两边同时减去x,得
x>﹣6,
不等式的两边同时乘以2,得
x>﹣12.
【点睛】
此题考查了解一元一次不等式,正确掌握解不等式的步骤及方法是解题的关键.
5、 (1)y1=﹣x+3
(2)n=a+b
(3)当a>b时,x>1;当a<b时,x<1
【解析】
【分析】
(1)把(1,2)、(2,b-a-3)分别代入y1=ax+b得到a、b的方程组,然后解方程组得到y1的函数表达式;
(2)把A(m,n)分别代入y1=ax+b和y2=bx+a中得到,先利用加减消元法求出m,然后得到n与a、b的关系式;
(3)先用a、b表示y3和y4,利用y3>y4得到(a-b)x+b-a>(b-a)x+a-b,然后解不等式即可.
(1)
解:把(1,2)、(2,b﹣a﹣3)分别代入y1=ax+b得
,
解得,
∴y1的函数表达式为y1=﹣x+3;
(2)
解:∵y1与y2的图象交于点A(m,n),
∴,
∴m=1,n=a+b;
(3)
解:y3=y1﹣y2=ax+b﹣(bx+a)=(a﹣b)x+b﹣a,
y4=y2﹣y1=bx+a﹣(ax+b)=(b﹣a)x+a﹣b,
∵y3>y4,
∴(a﹣b)x+b﹣a>(b﹣a)x+a﹣b,
整理得(a﹣b)x>a﹣b,
当a>b时,x>1;
当a<b时,x<1.
【点睛】
本题考查了待定系数法求一次函数解析式:设一次函数解析式为y=kx+b(k≠0),再把两组对应量代入,然后解关于k,b的二元一次方程组.从而得到一次函数解析式.也考查了一次函数的性质.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
