第五章 相交线与平行线 单元复习卷(含答案)2023-2024学年人教版七年级数学下册
文档属性
| 名称 | 第五章 相交线与平行线 单元复习卷(含答案)2023-2024学年人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 421.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览



文档简介
第五章 相交线与平行线 单元复习卷
一、单选题
1.如图,已知AB∥CD,∠1=56°,则∠2的度数是( )
A.34° B.56° C.65° D.124°
2.如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
A.30° B.140° C.50° D.60°
3.如图,下列条件中能判断的是( )
A. B.
C. D.
4.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知,,,则的度数是( )
A. B. C. D.
5.如图,在三角形中,,,,把三角形平移三角形位置,若,则下列结论中错误的是( )
A.ABDE B. C. D.
6.如图所示,直线AB和CD相交于点O,若∠COB=140°,则∠1、∠2的度数分别为( )
A.140°,40° B.40°,150° C.40°,140° D.150°,40°
7.如图是某公园里一处长方形风景欣赏区,长米,宽米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的正中间,从出口A到出口B所走的路线(图中虚线)长为( )
A.90米 B.98米 C.80米 D.88米
8.下列命题的逆命题不成立的是( )
A.直角三角形两条直角边的平方和等于斜边的平方
B.如果两个角是直角,那么它们相等
C.直角三角形中两锐角互余
D.线段垂直平分线上的点到线段两端的距离相等
9.下列说法正确的是( )
A.经过一点有且只有一条直线垂直于已知直线
B.互相垂直的两条直线一定相交
C.直线外一点到已知直线的垂线段叫点到直线的距离
D.两条直线都平行于第三条直线则这两条直线平行
10.如图,下列语句中,描述错误的是:
A.点O在直线AB上 B.直线AB与射线OP相交于点O
C.点P射线PO上 D.∠AOP与∠BOP互为补角
11.若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A.70° B.70°或86° C.86° D.30°或38°
12.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N;下列各角可以由∠END通过平移得到的角是( )
A.∠CNF B.∠AMF C.∠EMB D.∠AME
二、填空题
13.平面内有八条直线,两两相交最多有个交点,最少有个交点,则 .
14.如图,将ABE向右平移后得到△DCF(点B、C、E、F在同一条直线上),如果ABE的周长是12cm,四边形ABFD的周长是18cm,那么平移的距离为 cm.
15.如图,请你写出一个条件使,你写出的条件是 .
16.如图,,平分,,则 .
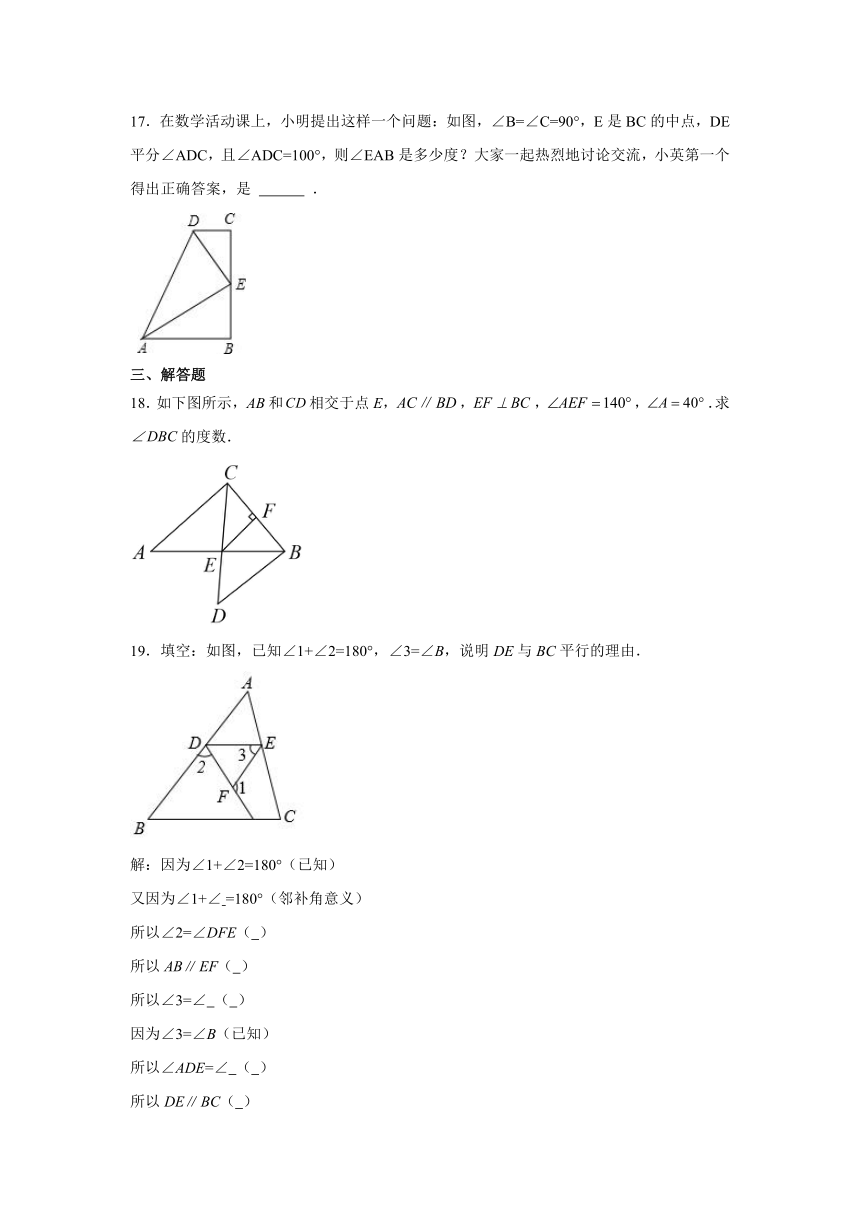
17.在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,且∠ADC=100°,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是 .
三、解答题
18.如下图所示,和相交于点E,,,,.求的度数.
19.填空:如图,已知∠1+∠2=180°,∠3=∠B,说明DE与BC平行的理由.
解:因为∠1+∠2=180°(已知)
又因为∠1+∠ =180°(邻补角意义)
所以∠2=∠DFE( )
所以ABEF( )
所以∠3=∠ ( )
因为∠3=∠B(已知)
所以∠ADE=∠ ( )
所以DEBC( )
20.如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.
(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数.
21.点在射线上,点、为射线上两个动点,满足,,平分.
(1)如图,当点在右侧时,求证:;
(2)如图,当点在左侧时,求证:;
(3)如图,在(2)的条件下,为延长线上一点,平分,交于点,平分,交于点,连接,若,,则的度数是多少.
参考答案
1--10BBBBC CDBDC 11--12BC
13.29
14.3
15.(答案不唯一)
16.30°
17.40°
18.解:∵EF⊥BC,
∴∠EFC=90°.
∵∠AEF=140°,∠A=40°,
∴∠AEF+∠A=180°.
∴AC∥EF.
∵AC∥BD,AC∥EF,
∴BD∥EF.
∴∠DBC=∠EFC=90°.
19.解:因为∠1+∠2=180°(已知)
又因为∠1+∠DFE=180°(邻补角意义)
所以∠2=∠DFE(同角的补角相等)
所以ABEF(内错角相等,两直线平行)
所以∠3=∠ADE(两直线平行,内错角相等)
因为∠3=∠B(已知)
所以∠ADE=∠B(等量代换)
所以DEBC(同位角相等,两直线平行)
故答案为:DFE;同角的补角相等;内错角相等,两直线平行;ADE;两直线平行,内错角相等;B;等量代换;同位角相等,两直线平行.
20.(1)解:∵OA平分∠COF, ∴∠COA=∠FOA=∠BOD,
∵OE⊥CD,
∴∠EOB+∠BOD=90°,
∴∠COA+∠EOB=90°,∠FOA+∠EOB=90°,
∴与∠EOB互余的角是:∠COA,∠FOA,∠BOD
(2)解:∵∠AOF=30°,由(1)知∠COA=∠FOA=∠BOD=30°, ∴∠DOF=180°﹣∠FOA﹣∠BOD=120°,
∵OE⊥CD,
∴∠BOE=90°﹣30°=60°
21.(1)平分,
,
又,
,
∴,
,
,
,
∴;
(2)过点作,交于点,如图,
由(1)同理可证:,
,
,,
,
;
(3)设,
则,,
,
平分,
,
,
,
,
,
,
,
,
,
,
解得:,
一、单选题
1.如图,已知AB∥CD,∠1=56°,则∠2的度数是( )
A.34° B.56° C.65° D.124°
2.如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
A.30° B.140° C.50° D.60°
3.如图,下列条件中能判断的是( )
A. B.
C. D.
4.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知,,,则的度数是( )
A. B. C. D.
5.如图,在三角形中,,,,把三角形平移三角形位置,若,则下列结论中错误的是( )
A.ABDE B. C. D.
6.如图所示,直线AB和CD相交于点O,若∠COB=140°,则∠1、∠2的度数分别为( )
A.140°,40° B.40°,150° C.40°,140° D.150°,40°
7.如图是某公园里一处长方形风景欣赏区,长米,宽米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的正中间,从出口A到出口B所走的路线(图中虚线)长为( )
A.90米 B.98米 C.80米 D.88米
8.下列命题的逆命题不成立的是( )
A.直角三角形两条直角边的平方和等于斜边的平方
B.如果两个角是直角,那么它们相等
C.直角三角形中两锐角互余
D.线段垂直平分线上的点到线段两端的距离相等
9.下列说法正确的是( )
A.经过一点有且只有一条直线垂直于已知直线
B.互相垂直的两条直线一定相交
C.直线外一点到已知直线的垂线段叫点到直线的距离
D.两条直线都平行于第三条直线则这两条直线平行
10.如图,下列语句中,描述错误的是:
A.点O在直线AB上 B.直线AB与射线OP相交于点O
C.点P射线PO上 D.∠AOP与∠BOP互为补角
11.若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A.70° B.70°或86° C.86° D.30°或38°
12.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N;下列各角可以由∠END通过平移得到的角是( )
A.∠CNF B.∠AMF C.∠EMB D.∠AME
二、填空题
13.平面内有八条直线,两两相交最多有个交点,最少有个交点,则 .
14.如图,将ABE向右平移后得到△DCF(点B、C、E、F在同一条直线上),如果ABE的周长是12cm,四边形ABFD的周长是18cm,那么平移的距离为 cm.
15.如图,请你写出一个条件使,你写出的条件是 .
16.如图,,平分,,则 .
17.在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,且∠ADC=100°,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是 .
三、解答题
18.如下图所示,和相交于点E,,,,.求的度数.
19.填空:如图,已知∠1+∠2=180°,∠3=∠B,说明DE与BC平行的理由.
解:因为∠1+∠2=180°(已知)
又因为∠1+∠ =180°(邻补角意义)
所以∠2=∠DFE( )
所以ABEF( )
所以∠3=∠ ( )
因为∠3=∠B(已知)
所以∠ADE=∠ ( )
所以DEBC( )
20.如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.
(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数.
21.点在射线上,点、为射线上两个动点,满足,,平分.
(1)如图,当点在右侧时,求证:;
(2)如图,当点在左侧时,求证:;
(3)如图,在(2)的条件下,为延长线上一点,平分,交于点,平分,交于点,连接,若,,则的度数是多少.
参考答案
1--10BBBBC CDBDC 11--12BC
13.29
14.3
15.(答案不唯一)
16.30°
17.40°
18.解:∵EF⊥BC,
∴∠EFC=90°.
∵∠AEF=140°,∠A=40°,
∴∠AEF+∠A=180°.
∴AC∥EF.
∵AC∥BD,AC∥EF,
∴BD∥EF.
∴∠DBC=∠EFC=90°.
19.解:因为∠1+∠2=180°(已知)
又因为∠1+∠DFE=180°(邻补角意义)
所以∠2=∠DFE(同角的补角相等)
所以ABEF(内错角相等,两直线平行)
所以∠3=∠ADE(两直线平行,内错角相等)
因为∠3=∠B(已知)
所以∠ADE=∠B(等量代换)
所以DEBC(同位角相等,两直线平行)
故答案为:DFE;同角的补角相等;内错角相等,两直线平行;ADE;两直线平行,内错角相等;B;等量代换;同位角相等,两直线平行.
20.(1)解:∵OA平分∠COF, ∴∠COA=∠FOA=∠BOD,
∵OE⊥CD,
∴∠EOB+∠BOD=90°,
∴∠COA+∠EOB=90°,∠FOA+∠EOB=90°,
∴与∠EOB互余的角是:∠COA,∠FOA,∠BOD
(2)解:∵∠AOF=30°,由(1)知∠COA=∠FOA=∠BOD=30°, ∴∠DOF=180°﹣∠FOA﹣∠BOD=120°,
∵OE⊥CD,
∴∠BOE=90°﹣30°=60°
21.(1)平分,
,
又,
,
∴,
,
,
,
∴;
(2)过点作,交于点,如图,
由(1)同理可证:,
,
,,
,
;
(3)设,
则,,
,
平分,
,
,
,
,
,
,
,
,
,
,
解得:,
