18.1 平行四边形(第4课时) 课件(共28张PPT)-【大单元教学】2023-2024学年八年级数学下册同步备课系列(人教版)
文档属性
| 名称 | 18.1 平行四边形(第4课时) 课件(共28张PPT)-【大单元教学】2023-2024学年八年级数学下册同步备课系列(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 740.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览



文档简介
新课导入
讲授新课
当堂检测
课堂小结
第十八章 平行四边形
18.1 平行四边形
18.1.4 三角形的中位线
温故知新
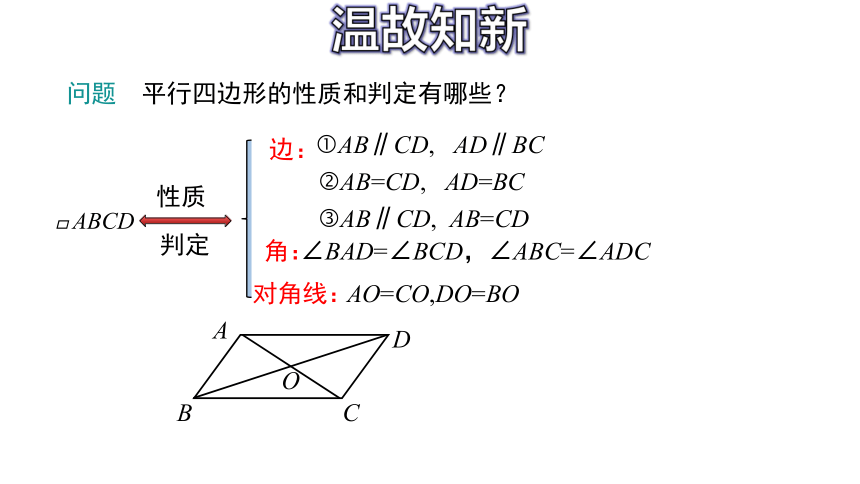
问题 平行四边形的性质和判定有哪些?
边:
角:
对角线:
B
O
D
A
C
?AB∥CD, AD∥BC
?AB=CD, AD=BC
?AB∥CD, AB=CD
∠BAD=∠BCD,∠ABC=∠ADC
AO=CO,DO=BO
判定
性质
古时候,有位老汉有四个儿子,他有一块三角形的耕地,想分给四个儿子。他们的儿子说必须分成一模一样的四部分才公平。这可难坏了老汉,你能帮帮他吗?
B
C
A
做思考小明同学把三角形分成了四个全等的三角形,猜一猜他是怎样做的?
做法:连接每两边的中点.
B
C
A
D·
·E
·
F
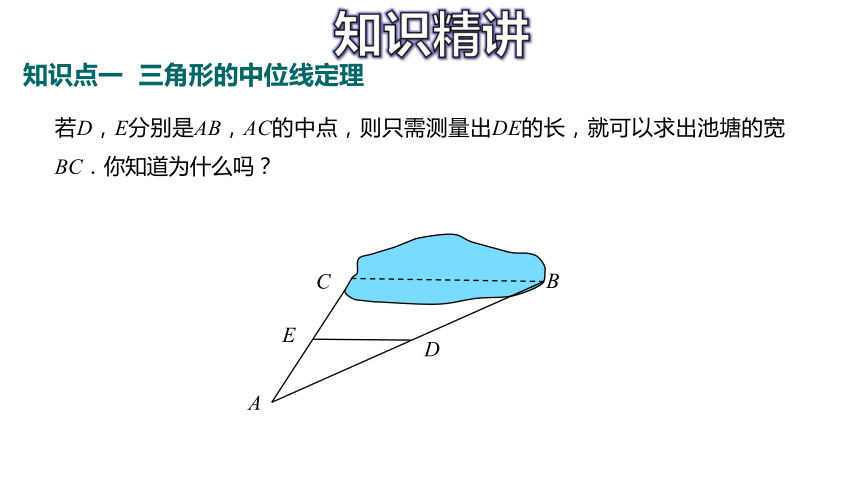
知识点一 三角形的中位线定理
知识精讲
若D,E分别是AB,AC的中点,则只需测量出DE的长,就可以求出池塘的宽BC.你知道为什么吗?
A
E
D
C
B
知识精讲
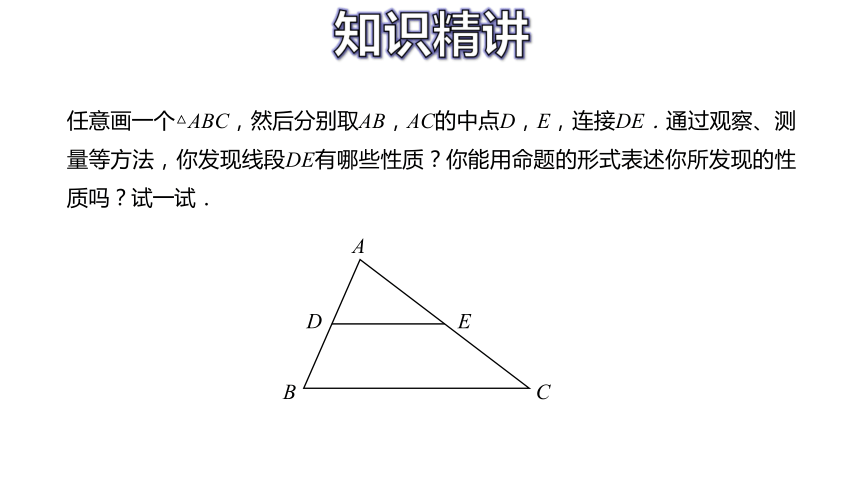
任意画一个△ABC,然后分别取AB,AC的中点D,E,连接DE.通过观察、测量等方法,你发现线段DE有哪些性质?你能用命题的形式表述你所发现的性质吗?试一试.
A
C
B
E
D
知识精讲
概念学习
定义:连接三角形两边中点的线段叫做三角形的中位线.
A
B
C
D
E
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE,则线段DE就称为△ABC的中位线.
知识精讲
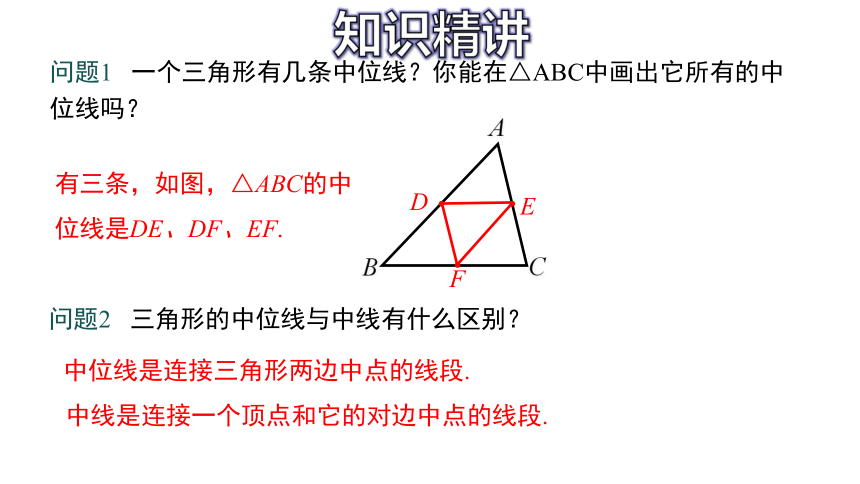
问题1 一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
A
B
C
D
E
F
有三条,如图,△ABC的中位线是DE、DF、EF.
问题2 三角形的中位线与中线有什么区别?
中位线是连接三角形两边中点的线段.
中线是连接一个顶点和它的对边中点的线段.
知识精讲
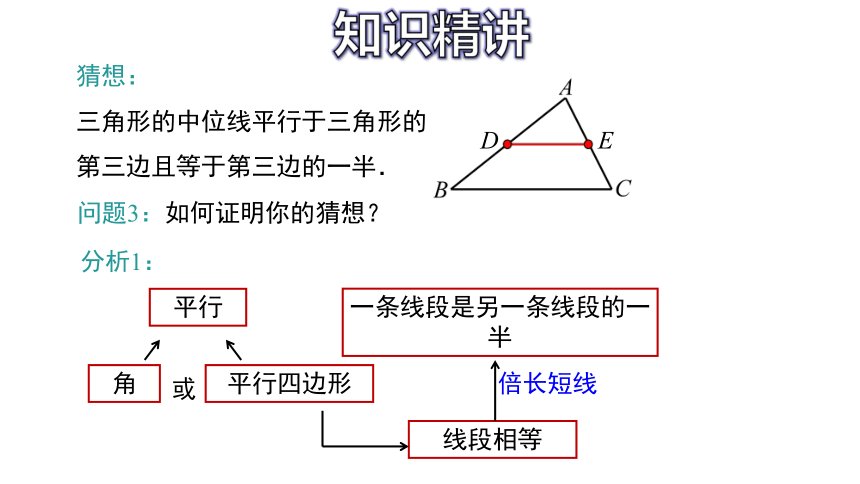
平行
角
平行四边形
或
线段相等
一条线段是另一条线段的一半
倍长短线
分析1:
D
E
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
问题3:如何证明你的猜想?
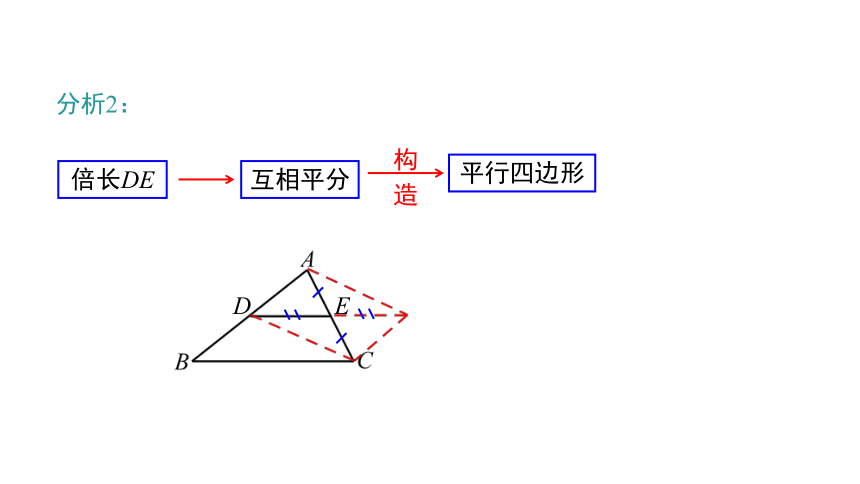
分析2:
D
E
互相平分
构造
平行四边形
倍长DE
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形,
∴CF AD ,
∴CF BD ,
又∵ ,
∴DF BC .
∴ DE∥BC, .
如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:
证一证
D
E
证明:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE,
证法2:
,AD=CF,
∴BD CF.
又∵ ,
∴DF BC .
∴ DE∥BC, .
∴CF AD ,
三角形的中位线平行于三角形的第三边且等于第三边的一半.
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
三角形中位线定理:
符号语言:
归纳总结
典型例题
典例精析
【例1】已知△ABC的面积是S,顺次连接各边中点E,G,F所得的四个三角形面积各是多少?
A
B
C
E
F
G
每个三角形的面积=14 S
?
解:根据三角形的中位线定理知,
EF= 12BC=BG,AE=12AB=EB,AF=12AC=EG,
?
故△AEF≌△EBG,
同理,△AEF≌△FGC, △GFE≌ △AEF.
所以,S△AEF =S△EBG =S△FGC =S△GFE=14S.
?
练一练
1、如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,
∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3,
∴∠1=∠2,
∴AD=DF=3,
∴AC=2AD=2DF=6.
1
2
3
知识精讲
2、如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
解:∵M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM= AB,PN= DC,PM∥AB,PN∥DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+(180°?∠NPB)=130°,
∴∠PMN=(180°?130°)÷ 2 =25°.
知识精讲
3、如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
证明:取AC的中点F,连接BF.
∵BD=AB,
∴BF为△ADC的中位线,∴DC=2BF.
∵E为AB的中点,AB=AC,
∴BE=CF,∠ABC=∠ACB.
∵BC=CB,∴△EBC≌△FCB,
∴CE=BF,
∴CD=2CE.
F
归纳:恰当地构造三角形中位线是解决线段倍分关系的关键.
知识点二 中点四边形
知识精讲
如图,任意画一个四边形,以四边形的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流.
知识精讲
证明:如图,连接AC.
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF∥AC,EF= AC,HG∥AC,HG= AC.
∴EF∥HG,EF=HG.
∴四边形EFGH为平行四边形.
中点四边形的定义:
依次连接任意四边形各边中点所得到的四边形称为中点四边形.
拓展:不管四边形的形状怎样改变,中点四边形始终是平行四边形.
知识精讲
任意四边形的中点四边形都是 ;
平行四边形的中点四边形是 ;
矩形的中点四边形是 ;
菱形的中点四边形是 ;
正方形的中点四边形是 。
平行四边形
平行四边形
矩形
菱形
正方形
小组合作探究:
知识精讲
归纳总结
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
原四边形两条对角线
连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
课堂练习
1.如图,DE是△ABC的中位线,若BC的长为3 cm,则DE的长是( )
A.2 cm
B.1.5 cm
C.1.2 cm
D.1 cm
B
2、如图,在?ABCD中,对角线AC,BD交于点O,E为边BC的中点,连接OE,若AB?4,则OE? .
2
A
B
C
D
O
E
3.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为 ( )
A.8 B.10 C.12 D.16
D
4.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24 cm,△OAB的周长是18 cm,则EF=________cm.
3
5.如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF=12BC,连结CD和EF.
(1)求证:DE=CF; (2)求EF的长.
?
(1)证明:∵D,E分别为AB,AC的中点,
∴DE为△ABC的中位线,
∴DE=12BC.
∵CF=12BC,∴DE=CF.
?
(2)解:由(1),知DE=CF.
又∵DE//BC,
∴四边形DEFC是平行四边形,∴DC=EF.
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,∴∠BDC=90°,
在Rt△BDC中,由勾股定理,得DC=????????2?????????2=3,即EF=3.
?
6.如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵?ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
课堂总结
三角形中位线
定义
定理
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,并且等于第三边的一半
应用
讲授新课
当堂检测
课堂小结
第十八章 平行四边形
18.1 平行四边形
18.1.4 三角形的中位线
温故知新
问题 平行四边形的性质和判定有哪些?
边:
角:
对角线:
B
O
D
A
C
?AB∥CD, AD∥BC
?AB=CD, AD=BC
?AB∥CD, AB=CD
∠BAD=∠BCD,∠ABC=∠ADC
AO=CO,DO=BO
判定
性质
古时候,有位老汉有四个儿子,他有一块三角形的耕地,想分给四个儿子。他们的儿子说必须分成一模一样的四部分才公平。这可难坏了老汉,你能帮帮他吗?
B
C
A
做思考小明同学把三角形分成了四个全等的三角形,猜一猜他是怎样做的?
做法:连接每两边的中点.
B
C
A
D·
·E
·
F
知识点一 三角形的中位线定理
知识精讲
若D,E分别是AB,AC的中点,则只需测量出DE的长,就可以求出池塘的宽BC.你知道为什么吗?
A
E
D
C
B
知识精讲
任意画一个△ABC,然后分别取AB,AC的中点D,E,连接DE.通过观察、测量等方法,你发现线段DE有哪些性质?你能用命题的形式表述你所发现的性质吗?试一试.
A
C
B
E
D
知识精讲
概念学习
定义:连接三角形两边中点的线段叫做三角形的中位线.
A
B
C
D
E
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE,则线段DE就称为△ABC的中位线.
知识精讲
问题1 一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
A
B
C
D
E
F
有三条,如图,△ABC的中位线是DE、DF、EF.
问题2 三角形的中位线与中线有什么区别?
中位线是连接三角形两边中点的线段.
中线是连接一个顶点和它的对边中点的线段.
知识精讲
平行
角
平行四边形
或
线段相等
一条线段是另一条线段的一半
倍长短线
分析1:
D
E
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
问题3:如何证明你的猜想?
分析2:
D
E
互相平分
构造
平行四边形
倍长DE
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形,
∴CF AD ,
∴CF BD ,
又∵ ,
∴DF BC .
∴ DE∥BC, .
如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:
证一证
D
E
证明:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE,
证法2:
,AD=CF,
∴BD CF.
又∵ ,
∴DF BC .
∴ DE∥BC, .
∴CF AD ,
三角形的中位线平行于三角形的第三边且等于第三边的一半.
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
三角形中位线定理:
符号语言:
归纳总结
典型例题
典例精析
【例1】已知△ABC的面积是S,顺次连接各边中点E,G,F所得的四个三角形面积各是多少?
A
B
C
E
F
G
每个三角形的面积=14 S
?
解:根据三角形的中位线定理知,
EF= 12BC=BG,AE=12AB=EB,AF=12AC=EG,
?
故△AEF≌△EBG,
同理,△AEF≌△FGC, △GFE≌ △AEF.
所以,S△AEF =S△EBG =S△FGC =S△GFE=14S.
?
练一练
1、如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,
∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3,
∴∠1=∠2,
∴AD=DF=3,
∴AC=2AD=2DF=6.
1
2
3
知识精讲
2、如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
解:∵M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM= AB,PN= DC,PM∥AB,PN∥DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+(180°?∠NPB)=130°,
∴∠PMN=(180°?130°)÷ 2 =25°.
知识精讲
3、如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
证明:取AC的中点F,连接BF.
∵BD=AB,
∴BF为△ADC的中位线,∴DC=2BF.
∵E为AB的中点,AB=AC,
∴BE=CF,∠ABC=∠ACB.
∵BC=CB,∴△EBC≌△FCB,
∴CE=BF,
∴CD=2CE.
F
归纳:恰当地构造三角形中位线是解决线段倍分关系的关键.
知识点二 中点四边形
知识精讲
如图,任意画一个四边形,以四边形的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流.
知识精讲
证明:如图,连接AC.
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF∥AC,EF= AC,HG∥AC,HG= AC.
∴EF∥HG,EF=HG.
∴四边形EFGH为平行四边形.
中点四边形的定义:
依次连接任意四边形各边中点所得到的四边形称为中点四边形.
拓展:不管四边形的形状怎样改变,中点四边形始终是平行四边形.
知识精讲
任意四边形的中点四边形都是 ;
平行四边形的中点四边形是 ;
矩形的中点四边形是 ;
菱形的中点四边形是 ;
正方形的中点四边形是 。
平行四边形
平行四边形
矩形
菱形
正方形
小组合作探究:
知识精讲
归纳总结
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
原四边形两条对角线
连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
课堂练习
1.如图,DE是△ABC的中位线,若BC的长为3 cm,则DE的长是( )
A.2 cm
B.1.5 cm
C.1.2 cm
D.1 cm
B
2、如图,在?ABCD中,对角线AC,BD交于点O,E为边BC的中点,连接OE,若AB?4,则OE? .
2
A
B
C
D
O
E
3.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为 ( )
A.8 B.10 C.12 D.16
D
4.如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24 cm,△OAB的周长是18 cm,则EF=________cm.
3
5.如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF=12BC,连结CD和EF.
(1)求证:DE=CF; (2)求EF的长.
?
(1)证明:∵D,E分别为AB,AC的中点,
∴DE为△ABC的中位线,
∴DE=12BC.
∵CF=12BC,∴DE=CF.
?
(2)解:由(1),知DE=CF.
又∵DE//BC,
∴四边形DEFC是平行四边形,∴DC=EF.
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,∴∠BDC=90°,
在Rt△BDC中,由勾股定理,得DC=????????2?????????2=3,即EF=3.
?
6.如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵?ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
课堂总结
三角形中位线
定义
定理
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,并且等于第三边的一半
应用
