18.1 平行四边形(第3课时) 课件(共44张PPT)-【大单元教学】2023-2024学年八年级数学下册同步备课系列(人教版)
文档属性
| 名称 | 18.1 平行四边形(第3课时) 课件(共44张PPT)-【大单元教学】2023-2024学年八年级数学下册同步备课系列(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 906.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 22:06:01 | ||
图片预览







文档简介
新课导入
讲授新课
当堂检测
课堂小结
第十八章 平行四边形
18.1 平行四边形
18.1.3 平行四边形的判定方法
温故知新
两组对边分别平行的四边形叫平行四边形.
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
问题1 平行四边形的定义是什么?有什么作用?
可以用平行四边形的定义来判定平行四边形,如:
问题2 除了两组对边分别平行,平行四边形还有哪些性质?
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
边:
角:
对角线:
思考 我们得到的这些逆命题是否都成立?这节课我们一起探讨一下吧.
问题3 平行四边形上面的三条性质的逆命题各是什么?
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形;
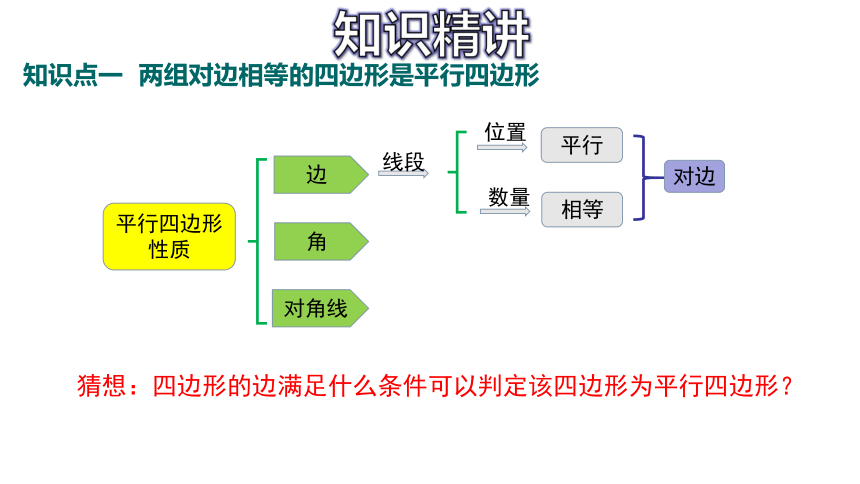
知识点一 两组对边相等的四边形是平行四边形
知识精讲
平行四边形
性质
边
角
对角线
线段
平行
相等
对边
位置
数量
猜想:四边形的边满足什么条件可以判定该四边形为平行四边形?
知识精讲
【探索】周末,小明的爸爸带着他回到了老家,看望乡下的爷爷.午饭后,小明的爷爷准备给他心爱的小菜园扎篱笆,地上散落着很多长短不一的细木棒.这时小明的爸爸说:“小明,你们现在已经开始学习平行四边形了,你能不能挑四根细木棒拼一个平行四边形呢?”
(2)他怎样才能拼接成平行四边形?
为什么?
你能为小明出谋划策吗?
(1)他应该选什么规格的细木棒?
知识精讲
用平行四边形的定义来判定,只要能说明四边形的两组对边是平行的,就可以证明木工师傅锯的木板是平行四边形.
定义判定:两组对边分别平行的四边形是平行四边形.
定义判定是一切判定的基础.
概念归纳
知识精讲
对平行四边形的判定,除了用定义判定,我们常常用平行四边形的性质来判定.
我们知道:平行四边形的两组对边相等.
反过来:两组对边分别相等的四边形是平行四边形吗?
知识精讲
B
D
A
C
取四根新木条,其中两根长度相等,另外两根长度也相等,能否在平面内将这四根细木条首位顺次相接搭成一个平行四边形?说说你的理由,并与同伴交流一下
典型例题
典例精析
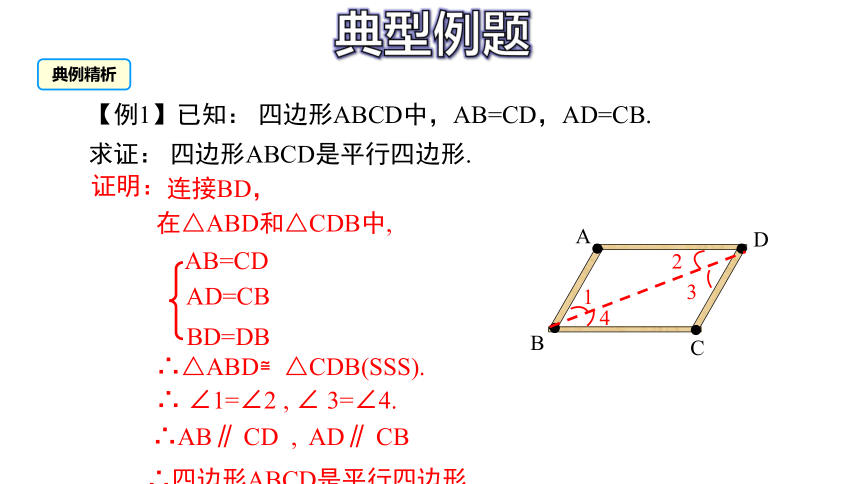
【例1】已知: 四边形ABCD中,AB=CD,AD=CB.
求证: 四边形ABCD是平行四边形.
A
B
C
D
连接BD,
在△ABD和△CDB中,
AB=CD
BD=DB
AD=CB
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥ CD , AD∥ CB
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
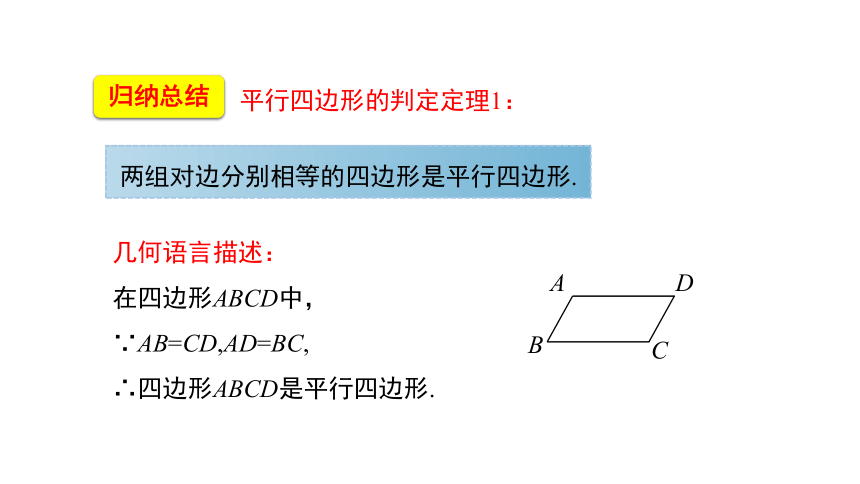
归纳总结
两组对边分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
B
D
A
C
平行四边形的判定定理1:
练一练
1、如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形.
解:∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
又∵BD=BA,BF=BC,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE.
同理可证△ABC≌△EFC,
∴AB=EF=AD,
∴四边形DAEF是平行四边形.
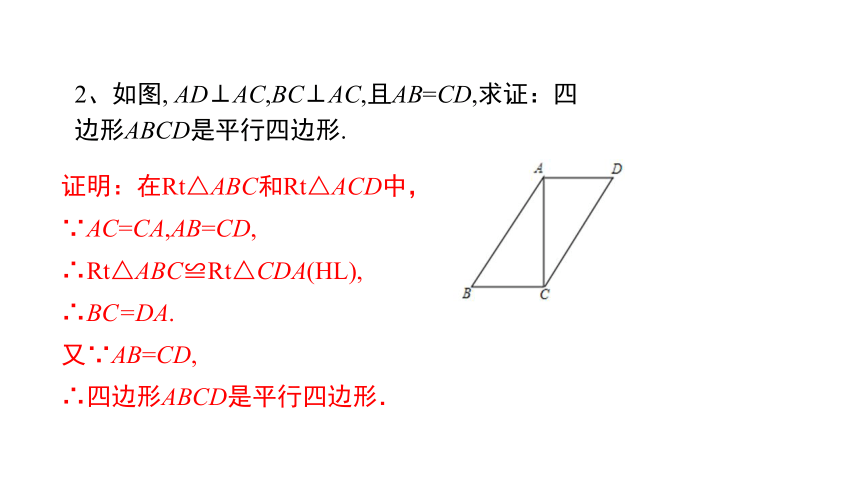
2、如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
知识点二 两组对角分别相等的四边形是平行四边形
知识精讲
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
又∵∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴ AD∥BC.
∴四边形ABCD是平行四边形.
同理得 AB∥ CD,
证明:
证一证
知识精讲
平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形.
概念归纳
几何语言描述:
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
B
D
A
C
典型例题
典例精析
【例2】如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
练一练
1.判断下列四边形是否为平行四边形:
A
D
C
B
110°
70°
110°
A
B
C
D
120°
60°
是
不是
2.能判定四边形ABCD是平行四边形的条件:
∠A:∠B:∠C:∠D的值为 ( )
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
D
知识点三 一组对边平行且相等的四边形是平行四边形
知识精讲
小明的爸爸又考验小明:“小明啊,如果只用两根相等的细木棒,你能不能摆成细木棒的四个端点恰好是一个平行四边形的四个顶点呢?”
(2)如果四边形有一组对边相等,那么还需要添加什么条件,才能使它成为平行四边形?
(1)你认为小明能做到吗?
知识精讲
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形
∵ AB CD, ∴四边形ABCD是平行四边形
∥
﹦
如图,在四边形ABCD中,AB∥CD,且AB=CD.求证:四边形ABCD是平行四边形.
证明:如图,连接AC.
∵AB∥CD,
∴∠BAC=∠ACD,
又∵ AB=CD,AC=CA,
∴ △BAC≌△DCA,
∴ BC=AD.
∴ 四边形ABCD是平行四边形.
D
C
B
A
平行四边形的判定定理3:
一组对边平行且相等的四边形是平行四边形.
概念归纳
几何语言描述:
在四边形ABCD中,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
典型例题
典例精析
【例3】如图,在?ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
B
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED= FB,ED∥FB.
∴四边形DFDE是平行四边形
(一组对边平行且相等的四边形是平行四边形).
练一练
1、如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE;
(2)连接DE,求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS),
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE,
∴CD∥BE.
又∵CD=BE,
∴四边形CBED是平行四边形.
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
2.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
知识点四 对角线互相平分的四边形是平行四边形
知识精讲
C
A
D
B
O
2.在直线a上截取OA=OC,在直线b上截取OB=OD,
1.画两条相交直线a、b,设交点为O.
a
b
连接AB、BC、CD、DA.
知识精讲
(1)线段AB、CD平行吗?为什么?
线段AD、BC呢?
解:在△AOB和△COD中,????????=????????(已知), ∠????????????=∠????????????(对顶角相等), ????????=????????(已知),
∴△AOB≌△COD(SAS).
∴∠BAO=∠DCO,
∴ AB∥CD.
?
A
D
B
O
a
b
C
同理AD∥BC.
(2)四边形ABCD是平行四边形吗?
由此你能得到什么结论?
由(1)AD∥BC,AB//DC,
A
D
B
O
a
b
C
∴四边形ABCD是平行四边形.
还有其他证明方法吗?
概念归纳
平行四边形的判定定理4:
对角线互相平分的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
B
O
D
A
C
典型例题
典例精析
【例4】如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
练一练
1、如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?说说你的理由.
解:四边形BMDN是平行四边形.
理由如下:连接BD交AC于O.
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°.
∵四边形ABCD是平行四边形,
∴OB=OD,AO=CO,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∴△ADN≌△CBM,∴AN=CM,
∴OA-AN=OC-CM,即ON=OM,
∴四边形BMDN是平行四边形.
O
知识点五 平行四边形的判定与性质的综合应用
知识精讲
【例5】如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?
解:BF=CE.理由如下:
∵DF∥BC,EF∥AC,
∴四边形FECD是平行四边形,∠FDB=∠DBE,
∴FD=CE.
∵BD平分∠ABC,
∴∠FBD=∠EBD,
∴∠FBD=∠FDB.
∴BF=FD.
∴BF=CE.
练一练
1、如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.
证明:由题意得∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′.
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴CE∥D′B,CE=D′B,
∴四边形BCED′是平行四边形.
此题利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,再结合平行四边形的判定及性质进行解题.
归纳
课堂练习
1.如图,已知四边形ABCD,则下列条件中不能判定四边形ABCD是平行四边形的是( )
A. AB=CD,AB∥CD
B. AB=CD,AD=BC
C. AB∥CD,AD∥BC
D. AB∥CD,AD=BC
D
B
A
D
C
2. 如图,在四边形ABCD中,E是AB边的中点,连接DE并延长,交CB的延长线于F点,BC=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )A.AB=CD
B.AB=CFC.∠A=∠C
D.∠F=∠ADE
D
A
B
C
D
E
F
3. 选择用反证法证明“已知:在△ABC中,∠C=90°.求证:∠A、∠B中至少有一个角不大于45°.”时,应先假设 ( )
A. ∠A>45°,∠B>45°
B. ∠A≥45°,∠B≥45°
C. ∠A<45°,∠B<45°
D.∠A≤45°,∠B≤45°
A
4. 在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AB∥CD;②AD=BC;③OA=OC;④OB=OD,从中任选两个,能使四边形ABCD为平行四边形的有______种.
3
5. 用反证法证明“三角形中最多有一个钝角”时,首先应假设这个三角形中________________________.
至少有两个角是钝角
6. 在四边形ABCD中,∠A= ∠C,∠B =∠D.四边形ABCD是平行四边形吗?证明你的结论.
解:四边形ABCD是平行四边形,
理由如下:
∵∠A+∠B+∠C+∠D=360°.
∵∠A=∠C,∠B =∠D,
∴∠C+∠B=180°,
∠C+∠D=180°,
∴AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形.
A
D
C
B
7. ?ABCD中,AF=CH,DE=BG,求证:EG和HF互相平分.
A
D
C
B
F
E
G
H
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A= ∠C.
∵DE=BG,
∴AD-ED=CB-GB,即AE=CG.
在△AEF和△CGH中,
????????=???????? ,∠????=∠????,????????=????????,
∴△AEF≌△CGH(SAS)
∴EF=GH.
同理FG=HE
∴四边形EFGH是平行四边形.
∴EG和HF互相平分.
?
8.如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD的中点.求证:
(1)△AOC≌△BOD;
(2)四边形AFBE是平行四边形.
证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD(AAS);
(2)∵△AOC≌△BOD,
∴CO=DO.
∵E、F分别是OC、OD的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE是平行四边形.
9.如图,△ABC中,AB=AC=10,D是BC边上的任意一点,分别作DF∥AB交AC于F,DE∥AC交AB于E,求DE+DF的值.
解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF.
又∵AB=AC=10,
∴∠B=∠C.
∵DF∥AB,
∴∠CDF=∠B,
∴∠CDF=∠C,
∴DF=CF,
∴DE+DF=AF+FC=AC=10.
10、如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________;CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形.
解:∵AP=tcm,CQ=2tcm,
AD=12cm,
∴PD=AD-AP=(12-t)cm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即12-t=2t,
解得t=4,
∴当t=4s时,四边形PDCQ是平行四边形.
(3)当t为何值时,四边形PDCQ是平行四边形?
课堂总结
平行四边形的判定
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
平行四边形的性质与判定的综合运用
讲授新课
当堂检测
课堂小结
第十八章 平行四边形
18.1 平行四边形
18.1.3 平行四边形的判定方法
温故知新
两组对边分别平行的四边形叫平行四边形.
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
问题1 平行四边形的定义是什么?有什么作用?
可以用平行四边形的定义来判定平行四边形,如:
问题2 除了两组对边分别平行,平行四边形还有哪些性质?
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
边:
角:
对角线:
思考 我们得到的这些逆命题是否都成立?这节课我们一起探讨一下吧.
问题3 平行四边形上面的三条性质的逆命题各是什么?
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形;
知识点一 两组对边相等的四边形是平行四边形
知识精讲
平行四边形
性质
边
角
对角线
线段
平行
相等
对边
位置
数量
猜想:四边形的边满足什么条件可以判定该四边形为平行四边形?
知识精讲
【探索】周末,小明的爸爸带着他回到了老家,看望乡下的爷爷.午饭后,小明的爷爷准备给他心爱的小菜园扎篱笆,地上散落着很多长短不一的细木棒.这时小明的爸爸说:“小明,你们现在已经开始学习平行四边形了,你能不能挑四根细木棒拼一个平行四边形呢?”
(2)他怎样才能拼接成平行四边形?
为什么?
你能为小明出谋划策吗?
(1)他应该选什么规格的细木棒?
知识精讲
用平行四边形的定义来判定,只要能说明四边形的两组对边是平行的,就可以证明木工师傅锯的木板是平行四边形.
定义判定:两组对边分别平行的四边形是平行四边形.
定义判定是一切判定的基础.
概念归纳
知识精讲
对平行四边形的判定,除了用定义判定,我们常常用平行四边形的性质来判定.
我们知道:平行四边形的两组对边相等.
反过来:两组对边分别相等的四边形是平行四边形吗?
知识精讲
B
D
A
C
取四根新木条,其中两根长度相等,另外两根长度也相等,能否在平面内将这四根细木条首位顺次相接搭成一个平行四边形?说说你的理由,并与同伴交流一下
典型例题
典例精析
【例1】已知: 四边形ABCD中,AB=CD,AD=CB.
求证: 四边形ABCD是平行四边形.
A
B
C
D
连接BD,
在△ABD和△CDB中,
AB=CD
BD=DB
AD=CB
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥ CD , AD∥ CB
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
归纳总结
两组对边分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
B
D
A
C
平行四边形的判定定理1:
练一练
1、如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形.
解:∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
又∵BD=BA,BF=BC,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE.
同理可证△ABC≌△EFC,
∴AB=EF=AD,
∴四边形DAEF是平行四边形.
2、如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
知识点二 两组对角分别相等的四边形是平行四边形
知识精讲
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
又∵∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴ AD∥BC.
∴四边形ABCD是平行四边形.
同理得 AB∥ CD,
证明:
证一证
知识精讲
平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形.
概念归纳
几何语言描述:
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
B
D
A
C
典型例题
典例精析
【例2】如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
练一练
1.判断下列四边形是否为平行四边形:
A
D
C
B
110°
70°
110°
A
B
C
D
120°
60°
是
不是
2.能判定四边形ABCD是平行四边形的条件:
∠A:∠B:∠C:∠D的值为 ( )
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
D
知识点三 一组对边平行且相等的四边形是平行四边形
知识精讲
小明的爸爸又考验小明:“小明啊,如果只用两根相等的细木棒,你能不能摆成细木棒的四个端点恰好是一个平行四边形的四个顶点呢?”
(2)如果四边形有一组对边相等,那么还需要添加什么条件,才能使它成为平行四边形?
(1)你认为小明能做到吗?
知识精讲
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形
∵ AB CD, ∴四边形ABCD是平行四边形
∥
﹦
如图,在四边形ABCD中,AB∥CD,且AB=CD.求证:四边形ABCD是平行四边形.
证明:如图,连接AC.
∵AB∥CD,
∴∠BAC=∠ACD,
又∵ AB=CD,AC=CA,
∴ △BAC≌△DCA,
∴ BC=AD.
∴ 四边形ABCD是平行四边形.
D
C
B
A
平行四边形的判定定理3:
一组对边平行且相等的四边形是平行四边形.
概念归纳
几何语言描述:
在四边形ABCD中,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
典型例题
典例精析
【例3】如图,在?ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
B
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED= FB,ED∥FB.
∴四边形DFDE是平行四边形
(一组对边平行且相等的四边形是平行四边形).
练一练
1、如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE;
(2)连接DE,求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS),
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE,
∴CD∥BE.
又∵CD=BE,
∴四边形CBED是平行四边形.
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
2.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
知识点四 对角线互相平分的四边形是平行四边形
知识精讲
C
A
D
B
O
2.在直线a上截取OA=OC,在直线b上截取OB=OD,
1.画两条相交直线a、b,设交点为O.
a
b
连接AB、BC、CD、DA.
知识精讲
(1)线段AB、CD平行吗?为什么?
线段AD、BC呢?
解:在△AOB和△COD中,????????=????????(已知), ∠????????????=∠????????????(对顶角相等), ????????=????????(已知),
∴△AOB≌△COD(SAS).
∴∠BAO=∠DCO,
∴ AB∥CD.
?
A
D
B
O
a
b
C
同理AD∥BC.
(2)四边形ABCD是平行四边形吗?
由此你能得到什么结论?
由(1)AD∥BC,AB//DC,
A
D
B
O
a
b
C
∴四边形ABCD是平行四边形.
还有其他证明方法吗?
概念归纳
平行四边形的判定定理4:
对角线互相平分的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
B
O
D
A
C
典型例题
典例精析
【例4】如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
练一练
1、如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?说说你的理由.
解:四边形BMDN是平行四边形.
理由如下:连接BD交AC于O.
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°.
∵四边形ABCD是平行四边形,
∴OB=OD,AO=CO,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∴△ADN≌△CBM,∴AN=CM,
∴OA-AN=OC-CM,即ON=OM,
∴四边形BMDN是平行四边形.
O
知识点五 平行四边形的判定与性质的综合应用
知识精讲
【例5】如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?
解:BF=CE.理由如下:
∵DF∥BC,EF∥AC,
∴四边形FECD是平行四边形,∠FDB=∠DBE,
∴FD=CE.
∵BD平分∠ABC,
∴∠FBD=∠EBD,
∴∠FBD=∠FDB.
∴BF=FD.
∴BF=CE.
练一练
1、如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.
证明:由题意得∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′.
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴CE∥D′B,CE=D′B,
∴四边形BCED′是平行四边形.
此题利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,再结合平行四边形的判定及性质进行解题.
归纳
课堂练习
1.如图,已知四边形ABCD,则下列条件中不能判定四边形ABCD是平行四边形的是( )
A. AB=CD,AB∥CD
B. AB=CD,AD=BC
C. AB∥CD,AD∥BC
D. AB∥CD,AD=BC
D
B
A
D
C
2. 如图,在四边形ABCD中,E是AB边的中点,连接DE并延长,交CB的延长线于F点,BC=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )A.AB=CD
B.AB=CFC.∠A=∠C
D.∠F=∠ADE
D
A
B
C
D
E
F
3. 选择用反证法证明“已知:在△ABC中,∠C=90°.求证:∠A、∠B中至少有一个角不大于45°.”时,应先假设 ( )
A. ∠A>45°,∠B>45°
B. ∠A≥45°,∠B≥45°
C. ∠A<45°,∠B<45°
D.∠A≤45°,∠B≤45°
A
4. 在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AB∥CD;②AD=BC;③OA=OC;④OB=OD,从中任选两个,能使四边形ABCD为平行四边形的有______种.
3
5. 用反证法证明“三角形中最多有一个钝角”时,首先应假设这个三角形中________________________.
至少有两个角是钝角
6. 在四边形ABCD中,∠A= ∠C,∠B =∠D.四边形ABCD是平行四边形吗?证明你的结论.
解:四边形ABCD是平行四边形,
理由如下:
∵∠A+∠B+∠C+∠D=360°.
∵∠A=∠C,∠B =∠D,
∴∠C+∠B=180°,
∠C+∠D=180°,
∴AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形.
A
D
C
B
7. ?ABCD中,AF=CH,DE=BG,求证:EG和HF互相平分.
A
D
C
B
F
E
G
H
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A= ∠C.
∵DE=BG,
∴AD-ED=CB-GB,即AE=CG.
在△AEF和△CGH中,
????????=???????? ,∠????=∠????,????????=????????,
∴△AEF≌△CGH(SAS)
∴EF=GH.
同理FG=HE
∴四边形EFGH是平行四边形.
∴EG和HF互相平分.
?
8.如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD的中点.求证:
(1)△AOC≌△BOD;
(2)四边形AFBE是平行四边形.
证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD(AAS);
(2)∵△AOC≌△BOD,
∴CO=DO.
∵E、F分别是OC、OD的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE是平行四边形.
9.如图,△ABC中,AB=AC=10,D是BC边上的任意一点,分别作DF∥AB交AC于F,DE∥AC交AB于E,求DE+DF的值.
解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF.
又∵AB=AC=10,
∴∠B=∠C.
∵DF∥AB,
∴∠CDF=∠B,
∴∠CDF=∠C,
∴DF=CF,
∴DE+DF=AF+FC=AC=10.
10、如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________;CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形.
解:∵AP=tcm,CQ=2tcm,
AD=12cm,
∴PD=AD-AP=(12-t)cm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即12-t=2t,
解得t=4,
∴当t=4s时,四边形PDCQ是平行四边形.
(3)当t为何值时,四边形PDCQ是平行四边形?
课堂总结
平行四边形的判定
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
平行四边形的性质与判定的综合运用
