【新结构】2023-2024学年福建省部分学校教学联盟高一下学期开学质量监测数学试题(含解析)
文档属性
| 名称 | 【新结构】2023-2024学年福建省部分学校教学联盟高一下学期开学质量监测数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 357.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览




文档简介
【新结构】2023-2024学年福建省部分学校教学联盟高一下学期开学质量监测数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设集合,则( )
A. B.
C. D.
2.( )
A. B. C. D.
3.已知,则下列结论正确的是
( )
A. B. C. D.
4.王昌龄是盛唐著名的边塞诗人,被誉为“七绝圣手”,其从军行传诵至今,“青海长云暗雪山,孤城遥望玉门关.黄沙百战穿金甲,不破楼兰终不还”,由此推断,其中最后一句“攻破楼兰”是“返回家乡”的
( )
A. 必要条件 B. 充分条件
C. 充要条件 D. 既不充分又不必要条件
5.已知命题若为假命题,则实数的取值范围是
( )
A. B. C. D.
6.函数的图象大致为
( )
A. B.
C. D.
7.“学如逆水行舟,不进则退心似平原跑马,易放难收”,增广贤文是勉励人们专心学习的如果每天的“进步”率都是,那么一年后是如果每天的“落后”率都是,那么一年后是一年后“进步”的是“落后”的倍现假设每天的“进步”率和“落后”率都是,要使“进步”的是“落后”的倍,则大约需要经过参考数据:,( )
A. 天 B. 天 C. 天 D. 天
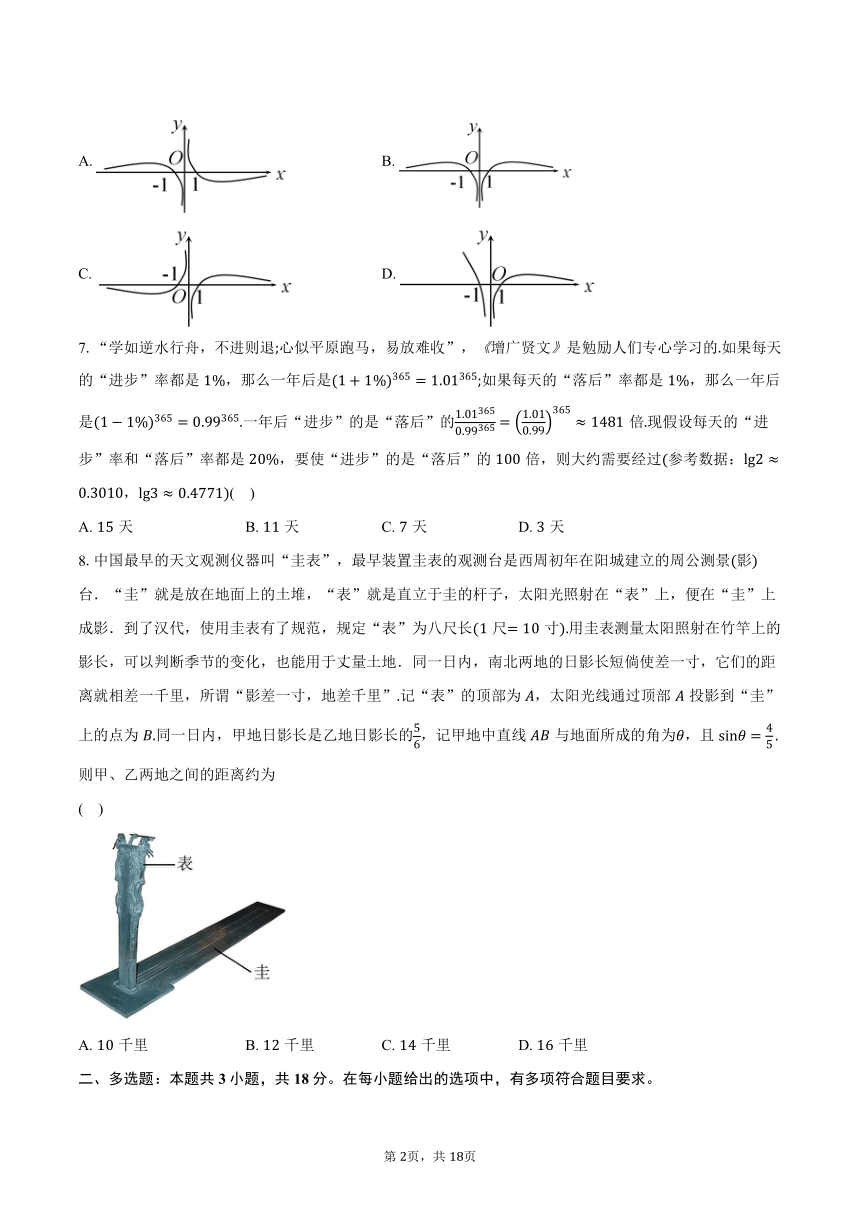
8.中国最早的天文观测仪器叫“圭表”,最早装置圭表的观测台是西周初年在阳城建立的周公测景影台.“圭”就是放在地面上的土堆,“表”就是直立于圭的杆子,太阳光照射在“表”上,便在“圭”上成影.到了汉代,使用圭表有了规范,规定“表”为八尺长尺寸用圭表测量太阳照射在竹竿上的影长,可以判断季节的变化,也能用于丈量土地.同一日内,南北两地的日影长短倘使差一寸,它们的距离就相差一千里,所谓“影差一寸,地差千里”记“表”的顶部为,太阳光线通过顶部投影到“圭”上的点为同一日内,甲地日影长是乙地日影长的,记甲地中直线与地面所成的角为,且则甲、乙两地之间的距离约为
( )
A. 千里 B. 千里 C. 千里 D. 千里
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.函数的部分图象如图,则
( )
A. 是函数的一条对称轴 B. 是函数的一条对称轴
C. D.
10.已知函数,的定义域均为,且,若是的对称轴,且,则下列结论正确的是
( )
A. 是奇函数 B. 是的对称中心
C. 是的周期 D.
11.波恩哈德黎曼是德国著名的数学家他在数学分析、微分几何方面作出过重要贡献,开创了黎曼几何,并给后来的广义相对论提供了数学基础他提出了著名的黎曼函数,该函数的定义域为,其解析式为:,下列关于黎曼函数的说法正确的是
( )
A.
B.
C.
D. 关于的不等式的解集为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知全集,,,指出图中阴影部分表示的集合是 .
13.已知,则 .
14.已知函数,若,则关于的不等式的解集为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知函数的图象经过点.
求的值,判断的单调性并说明理由;
若存在,不等式成立,求实数的取值范围.
16.本小题分
杭州,作为年亚洲运动会的举办城市,以其先进的科技和创新能力再次吸引了全球的目光其中首次采用“机器狗”在田径赛场上运送铁饼等,迅速成为了全场的焦点已知购买台“机器狗”的总成本为.
若使每台“机器狗”的平均成本最低,问应买多少台
现安排标明“汪”、“汪”、“汪”的台“机器狗”在同一场次运送铁饼,且运送的距离都是米台“机器狗”所用时间单位:秒分别为,,“汪”有一半的时间以速度单位:米秒奔跑,另一半的时间以速度奔跑;“汪”全程以速度奔跑;“汪”有一半的路程以速度奔跑,另一半的路程以速度奔跑,其中,,且则哪台机器狗用的时间最少请说明理由.
17.本小题分
筒车亦称“水转筒车”一种以水流作动力,取水灌田的工具据史料记载,筒车发明于隋而盛于唐,距今已有多年的历史.这种靠水力自动的古老筒车,在家乡郁郁葱葱的山间、溪流间构成了一幅幅远古的田园春色图.水转筒车是利用水力转动的筒车,必须架设在水流湍急的岸边.水激轮转,浸在水中的小筒装满了水带到高处,筒口向下,水即自筒中倾泻入轮旁的水槽而汇流入田.某乡间有一筒车,其最高点到水面的距离为,筒车直径为,设置有个盛水筒,均匀分布在筒车转轮上,筒车上的每一个盛水筒都做逆时针匀速圆周运动,筒车转一周需要,如图,盛水筒视为质点的初始位置距水面的距离为.
盛水筒经过后距离水面的高度为单位:,求筒车转动一周的过程中,关于的函数的解析式;
盛水筒视为质点与盛水筒相邻,设盛水筒在盛水筒的顺时针方向相邻处,求盛水筒与盛水筒的高度差的最大值结果用含的代数式表示,及此时对应的.
参考公式:,
18.本小题分
某药品可用于治疗某种疾病,经检测知每注射药品,从注射时间起血药浓度单位:与药品在体内时间单位:小时的关系如下:当血药浓度不低于时才能起到有效治疗的作用,每次注射药品不超过.
若注射药品,求药品的有效治疗时间;
若多次注射,则某一时刻体内血药浓度为每次注射后相应时刻血药浓度之和.已知病人第一次注射药品,小时之后又注射药品,要使随后的小时内药品能够持续有效消疗,求的最小值.
19.本小题分
已知函数.
求函数的单调递增区间;
若,存在,对任意,有恒成立,求的最小值;
若函数在内恰有个零点,求与的值.
答案和解析
1.【答案】
【解析】【分析】
本题考查了集合的交集运算,解绝对值不等式,属于基础题.
求出集合,根据集合的交集运算即可求得答案.
【解答】
解:由题意得,
故,
故选:.
2.【答案】
【解析】【分析】
利用诱导公式及特殊角的三角函数值计算即可.
【解答】
解:.
故选:
3.【答案】
【解析】【分析】
直接由作差法逐一判断即可.
【解答】
解:对于,由题意,即,故 A错误;
对于,由题意,即,故 B错误;
对于,由题意,即,故 C正确;
对于,由题意,即,故 D错误.
故选:.
4.【答案】
【解析】【分析】
本题主要考查了充分必要条件的判断,属于简单题.
先阅读理解题意,再利用充分必要条件判断即可得解.
【解答】
解:由题意可知:“返回家乡”则可推出“攻破楼兰”,
但是“攻破楼兰”不一定能推出“返回家乡”,
故“攻破楼兰”是“返回家乡”必要条件.
故选A.
5.【答案】
【解析】【分析】
先得到为真命题,从而根据根的判别式列出不等式,求出答案.
【解答】
解:为真命题,即,
解得:,
故实数的取值范围是.
故选:
6.【答案】
【解析】【分析】
根据函数的奇偶性、特殊点的函数值确定正确答案.
【解答】
解:的定义域为,
,所以是奇函数,图象关于原点对称,排除选项.
,排除选项.
所以正确的为选项.
故选:
7.【答案】
【解析】【分析】
依题意得,利用对数的运算性质即可求解.
【解答】
解:经过天后,“进步”的是“落后”的比,
所以,两边取以为底的对数得,解得.
要使“进步”的是“落后”的倍,则大约需要经过天.
故选:
8.【答案】
【解析】【分析】
根据给定条件,求出甲地、乙地的日影长,即可计算甲、乙两地的距离作答.
【解答】
解:依题意,甲地中线段的长为寸,则甲地的日影长为寸,
于是乙地的日影长为寸,甲、乙两地的日影长相差寸,
所以甲、乙两地之间的距离是千里.
故选:
9.【答案】
【解析】【分析】
点是函数图象的对称中心,且在函数的一个单调增区间内,则,令函数周期为,由图象知,由,得函数图象的对称轴:,,据此分析即可.
【解答】
解:依题意,点是函数的图象对称中心,
且在函数的一个单调增区间内,
则,,即,,
令函数周期为,由图象知
即有,而,则有,
因此,,解得,
而,则,,,故 C错误D正确;
由,得函数图象的对称轴:,,
当时,,当时,,故 AB正确.
故选:.
10.【答案】
【解析】【分析】
根据对称性和已知条件得到,判断;结合已知条件变形得到,判断;利用赋值法求得,判断;根据条件得到的周期为,对称中心为,从而得到函数值即可求解,判断.
【解答】
解:对于,因为是的对称轴,所以,
又因为,所以,故,
即为偶函数,故 A错误;
对于,因为,所以,
又因为,联立得,
所以的图像关于点中心对称,故 B正确;
对于,因为,,则,即;
因为,则,即,则;
显然,所以不是的周期,故 C错误;
对于,因为是的对称轴,所以,
又因为,即,
则,所以,
所以,即,所以周期为,
因为周期为,对称中心为,所以,
当时,代入,即,所以,
所以,又是的对称轴,所以,
所以,故 D正确,
故选:.
11.【答案】
【解析】【分析】
根据黎曼函数的定义域分类对函数进行分析,再对每一个选项逐一分析判断,即可求出结果.
【解答】
解:对于选项A,当时,,当时,,而,
当时,,若是无理数,则是无理数,有,
若是有理数,则是有理数,当为正整数,为最简真分数,
则为正整数,为最简真分数,此时,
综上,时,所以选项 A正确,
对于选项B,当和无理数时,,显然有,
当是正整数,是最简真分数时,
,,故,
当时,,有
当时,,,有
当为无理数,时,,有
综上,所以选项 B正确;
对于选项C,取,则,而,所以选项 C错误,
对于选项D,若或或内的无理数,此时,显然不成立,
当为正整数,互质,由,得到,
整理得到,又为正整数,互质,所以或均满足,所以可以取或,所以选项 D错误,
故选:.
12.【答案】
【解析】【分析】
根据集合的运算求得,可得,结合图中阴影部分表示的集合为,即可得答案.
【解答】
解:由于全集,,,
故,
则,
故图中阴影部分表示的集合为,
故答案为:
13.【答案】
【解析】【分析】
根据倍角公式即的取值范围从而可求解.
【解答】
解:由题意知,,所以,
所以,,
所以.
故答案为:.
14.【答案】
【解析】【分析】
计算出,函数关于点中心对称,得到有唯一的解,求出函数的单调性,结合题目条件得到,进而得到分段函数解析式,计算出,故,结合函数单调性得到不等式.
【解答】
解:由题意,得,,
所以,即函数关于点中心对称.
因为恒成立,所以当时,,
当时,.
所以有唯一的解.
当时,,函数单调递增,
当时,,函数单调递增,
当时,,函数单调递增,
又,,
故在上单调递增,
,
由对称性可知,
下面证明,过程如下:
若时,则,且,则,,
,
此时,
同理可得当时,,
当,即时,,,满足,即.
故
当时,,
当时,令,解得,
当时,,
又不等式,所以.
由,得由,得.
所以原不等式的解集为.
故答案为:
点睛:函数的对称性:
若,则函数关于中心对称,
若,则函数关于对称
15.【答案】解:函数经过点,
所以,解得,即,
,
则是上的单调递增函数,理由如下:
任取、,且,则,
则,
所以,即,
所以是定义域上的单调递增函数.
因为,
故是奇函数且在上单调递增,
则不等式等价于,
所以,即,
即存在,不等式有解,
即在上有解,
由,可得,
由对勾函数性质易知:在单调递减,在单调递增,
且,故在的最大值为,
所以,即
所以,
即实数的取值范围是.
【解析】由函数经过点求的值,得到的解析式,用定义法证明函数的单调性;
根据函数的奇偶性和单调性,不等式转化为在上有解,利用参数分离法结合基本不等式可求出实数的取值范围.
16.【答案】解:由题意,购买台“机器狗”的总成本为,
则每台机器狗的平均成本为,
当且仅当时,即时,等号成立,
所以,若使每台“机器狗”的平均成本最低,应买台
由题意,“汪”满足,可得,
“汪”满足,可得,
“汪”满足,
,,
所以 ,
因为,,且,
所以可得,
则,
所以,所以“汪”用的时间最少.
【解析】平均成本为,利用比较不等式,即可求解函数的最值;
利用速度,时间和路程的关系,分别求解,,,再根据不等式,比较时间大小,即可求解.
17.【答案】解:以筒车转轮的中心为原点,与水面平行的直线为轴建立平面直角坐标系,
设,,
由题意知,,,
,,即,
当时,,解得,
结合图象初始位置可知,
又因为,所以,
综上,,;
经过后距离水面的高度,
由题意知,
所以经过后距离水面的高度,
则盛水筒与盛水筒的高度差为,
利用,
,
当,,即,时,取最大值,
又因为,所以当或时,取最大值,
综上,盛水筒与盛水筒的高度差的最大值为,此时或.
【解析】本题考查三角函数模型的应用、函数的图象与性质,考查运算求解能力,是较难题.
设,,直接由题意求出,,,的值;
易得,分别求出经过相邻两个盛水筒距离水面的高度,作差后利用三角函数求最值.
18.【答案】解:注射该药品,其浓度为
当时,,解得;
当时,,解得.
所以一次注射该药品,则药物有效时间可达小时.
设从第一次注射起,经小时后,
其浓度,则,
因为,
当时,即时,等号成立.
,当时,,
所以,因为,
解得,所以.
当时,,,所以不能保证持续有效,
答:要使随后的小时内药品能够持续有效治疗,的最小值为.
【解析】由血药浓度与药品在体内时间的关系,计算血药浓度不低于时对应的时间段;
由两次注射的血药浓度之和不低于,利用基本不等式求的最小值.
方法点睛:
分段函数模型的应用:
在现实生活中,很多问题的两变是之间的关系,不能用同一个关系式给出,而是由几个不同的关系式构成分段函数,分段函数模型适用于描述在不同区间上函数值的变化情况,分段函数主要是每一段上自变量变化所遵循的规律不同,可以先将其作为几个不同问题,将各段的规律找出来,再将其合在一起,要注意各段变量的范围,特别是端点.
19.【答案】解:
令,
得
函数的单调递增区间为
令,
则
可得,当即时,;
当即时,
存在,对任意,有恒成立,
为的最小值,为的最大值,
,,
,
.
令,
方程可化为,
令,则,
当时,,,此时函数在上有个零点,
,适合题意;
当时,在内有一解,
在或内有一取值,则此时函数在上有个零点,不适合题意;
当时,,此时函数在上有个零点,
,适合题意;
当时,或,或,则此时函数在上有个零点,不适合题意;
当时,在和内各有一解,在和内各有一取值,
则此时函数在上有个零点,不适合题意;
当时,,,则此时函数在上有个零点,不适合题意.
综上所述,,,或,.
【解析】根据二倍角公式和辅助角公式化简,结合三角函数增区间求法计算即可;
根据题意写出函数,结合平方关系进行换元,结合新元范围与二次函数的知识求解最值,得到,进而得到答案;
将原题意转化为,令,则,再分类讨论进行取舍即可得到答案.
关键点点睛:本题考查三角函数的综合应用问题关键点在于换元法的运用,例如中令,则,进而转化为二次函数;第中方程可化为,令,则,通过换元进而由繁化简进行求解本题考查转化与化归、分类与整合能力,属于难题.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设集合,则( )
A. B.
C. D.
2.( )
A. B. C. D.
3.已知,则下列结论正确的是
( )
A. B. C. D.
4.王昌龄是盛唐著名的边塞诗人,被誉为“七绝圣手”,其从军行传诵至今,“青海长云暗雪山,孤城遥望玉门关.黄沙百战穿金甲,不破楼兰终不还”,由此推断,其中最后一句“攻破楼兰”是“返回家乡”的
( )
A. 必要条件 B. 充分条件
C. 充要条件 D. 既不充分又不必要条件
5.已知命题若为假命题,则实数的取值范围是
( )
A. B. C. D.
6.函数的图象大致为
( )
A. B.
C. D.
7.“学如逆水行舟,不进则退心似平原跑马,易放难收”,增广贤文是勉励人们专心学习的如果每天的“进步”率都是,那么一年后是如果每天的“落后”率都是,那么一年后是一年后“进步”的是“落后”的倍现假设每天的“进步”率和“落后”率都是,要使“进步”的是“落后”的倍,则大约需要经过参考数据:,( )
A. 天 B. 天 C. 天 D. 天
8.中国最早的天文观测仪器叫“圭表”,最早装置圭表的观测台是西周初年在阳城建立的周公测景影台.“圭”就是放在地面上的土堆,“表”就是直立于圭的杆子,太阳光照射在“表”上,便在“圭”上成影.到了汉代,使用圭表有了规范,规定“表”为八尺长尺寸用圭表测量太阳照射在竹竿上的影长,可以判断季节的变化,也能用于丈量土地.同一日内,南北两地的日影长短倘使差一寸,它们的距离就相差一千里,所谓“影差一寸,地差千里”记“表”的顶部为,太阳光线通过顶部投影到“圭”上的点为同一日内,甲地日影长是乙地日影长的,记甲地中直线与地面所成的角为,且则甲、乙两地之间的距离约为
( )
A. 千里 B. 千里 C. 千里 D. 千里
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.函数的部分图象如图,则
( )
A. 是函数的一条对称轴 B. 是函数的一条对称轴
C. D.
10.已知函数,的定义域均为,且,若是的对称轴,且,则下列结论正确的是
( )
A. 是奇函数 B. 是的对称中心
C. 是的周期 D.
11.波恩哈德黎曼是德国著名的数学家他在数学分析、微分几何方面作出过重要贡献,开创了黎曼几何,并给后来的广义相对论提供了数学基础他提出了著名的黎曼函数,该函数的定义域为,其解析式为:,下列关于黎曼函数的说法正确的是
( )
A.
B.
C.
D. 关于的不等式的解集为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知全集,,,指出图中阴影部分表示的集合是 .
13.已知,则 .
14.已知函数,若,则关于的不等式的解集为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知函数的图象经过点.
求的值,判断的单调性并说明理由;
若存在,不等式成立,求实数的取值范围.
16.本小题分
杭州,作为年亚洲运动会的举办城市,以其先进的科技和创新能力再次吸引了全球的目光其中首次采用“机器狗”在田径赛场上运送铁饼等,迅速成为了全场的焦点已知购买台“机器狗”的总成本为.
若使每台“机器狗”的平均成本最低,问应买多少台
现安排标明“汪”、“汪”、“汪”的台“机器狗”在同一场次运送铁饼,且运送的距离都是米台“机器狗”所用时间单位:秒分别为,,“汪”有一半的时间以速度单位:米秒奔跑,另一半的时间以速度奔跑;“汪”全程以速度奔跑;“汪”有一半的路程以速度奔跑,另一半的路程以速度奔跑,其中,,且则哪台机器狗用的时间最少请说明理由.
17.本小题分
筒车亦称“水转筒车”一种以水流作动力,取水灌田的工具据史料记载,筒车发明于隋而盛于唐,距今已有多年的历史.这种靠水力自动的古老筒车,在家乡郁郁葱葱的山间、溪流间构成了一幅幅远古的田园春色图.水转筒车是利用水力转动的筒车,必须架设在水流湍急的岸边.水激轮转,浸在水中的小筒装满了水带到高处,筒口向下,水即自筒中倾泻入轮旁的水槽而汇流入田.某乡间有一筒车,其最高点到水面的距离为,筒车直径为,设置有个盛水筒,均匀分布在筒车转轮上,筒车上的每一个盛水筒都做逆时针匀速圆周运动,筒车转一周需要,如图,盛水筒视为质点的初始位置距水面的距离为.
盛水筒经过后距离水面的高度为单位:,求筒车转动一周的过程中,关于的函数的解析式;
盛水筒视为质点与盛水筒相邻,设盛水筒在盛水筒的顺时针方向相邻处,求盛水筒与盛水筒的高度差的最大值结果用含的代数式表示,及此时对应的.
参考公式:,
18.本小题分
某药品可用于治疗某种疾病,经检测知每注射药品,从注射时间起血药浓度单位:与药品在体内时间单位:小时的关系如下:当血药浓度不低于时才能起到有效治疗的作用,每次注射药品不超过.
若注射药品,求药品的有效治疗时间;
若多次注射,则某一时刻体内血药浓度为每次注射后相应时刻血药浓度之和.已知病人第一次注射药品,小时之后又注射药品,要使随后的小时内药品能够持续有效消疗,求的最小值.
19.本小题分
已知函数.
求函数的单调递增区间;
若,存在,对任意,有恒成立,求的最小值;
若函数在内恰有个零点,求与的值.
答案和解析
1.【答案】
【解析】【分析】
本题考查了集合的交集运算,解绝对值不等式,属于基础题.
求出集合,根据集合的交集运算即可求得答案.
【解答】
解:由题意得,
故,
故选:.
2.【答案】
【解析】【分析】
利用诱导公式及特殊角的三角函数值计算即可.
【解答】
解:.
故选:
3.【答案】
【解析】【分析】
直接由作差法逐一判断即可.
【解答】
解:对于,由题意,即,故 A错误;
对于,由题意,即,故 B错误;
对于,由题意,即,故 C正确;
对于,由题意,即,故 D错误.
故选:.
4.【答案】
【解析】【分析】
本题主要考查了充分必要条件的判断,属于简单题.
先阅读理解题意,再利用充分必要条件判断即可得解.
【解答】
解:由题意可知:“返回家乡”则可推出“攻破楼兰”,
但是“攻破楼兰”不一定能推出“返回家乡”,
故“攻破楼兰”是“返回家乡”必要条件.
故选A.
5.【答案】
【解析】【分析】
先得到为真命题,从而根据根的判别式列出不等式,求出答案.
【解答】
解:为真命题,即,
解得:,
故实数的取值范围是.
故选:
6.【答案】
【解析】【分析】
根据函数的奇偶性、特殊点的函数值确定正确答案.
【解答】
解:的定义域为,
,所以是奇函数,图象关于原点对称,排除选项.
,排除选项.
所以正确的为选项.
故选:
7.【答案】
【解析】【分析】
依题意得,利用对数的运算性质即可求解.
【解答】
解:经过天后,“进步”的是“落后”的比,
所以,两边取以为底的对数得,解得.
要使“进步”的是“落后”的倍,则大约需要经过天.
故选:
8.【答案】
【解析】【分析】
根据给定条件,求出甲地、乙地的日影长,即可计算甲、乙两地的距离作答.
【解答】
解:依题意,甲地中线段的长为寸,则甲地的日影长为寸,
于是乙地的日影长为寸,甲、乙两地的日影长相差寸,
所以甲、乙两地之间的距离是千里.
故选:
9.【答案】
【解析】【分析】
点是函数图象的对称中心,且在函数的一个单调增区间内,则,令函数周期为,由图象知,由,得函数图象的对称轴:,,据此分析即可.
【解答】
解:依题意,点是函数的图象对称中心,
且在函数的一个单调增区间内,
则,,即,,
令函数周期为,由图象知
即有,而,则有,
因此,,解得,
而,则,,,故 C错误D正确;
由,得函数图象的对称轴:,,
当时,,当时,,故 AB正确.
故选:.
10.【答案】
【解析】【分析】
根据对称性和已知条件得到,判断;结合已知条件变形得到,判断;利用赋值法求得,判断;根据条件得到的周期为,对称中心为,从而得到函数值即可求解,判断.
【解答】
解:对于,因为是的对称轴,所以,
又因为,所以,故,
即为偶函数,故 A错误;
对于,因为,所以,
又因为,联立得,
所以的图像关于点中心对称,故 B正确;
对于,因为,,则,即;
因为,则,即,则;
显然,所以不是的周期,故 C错误;
对于,因为是的对称轴,所以,
又因为,即,
则,所以,
所以,即,所以周期为,
因为周期为,对称中心为,所以,
当时,代入,即,所以,
所以,又是的对称轴,所以,
所以,故 D正确,
故选:.
11.【答案】
【解析】【分析】
根据黎曼函数的定义域分类对函数进行分析,再对每一个选项逐一分析判断,即可求出结果.
【解答】
解:对于选项A,当时,,当时,,而,
当时,,若是无理数,则是无理数,有,
若是有理数,则是有理数,当为正整数,为最简真分数,
则为正整数,为最简真分数,此时,
综上,时,所以选项 A正确,
对于选项B,当和无理数时,,显然有,
当是正整数,是最简真分数时,
,,故,
当时,,有
当时,,,有
当为无理数,时,,有
综上,所以选项 B正确;
对于选项C,取,则,而,所以选项 C错误,
对于选项D,若或或内的无理数,此时,显然不成立,
当为正整数,互质,由,得到,
整理得到,又为正整数,互质,所以或均满足,所以可以取或,所以选项 D错误,
故选:.
12.【答案】
【解析】【分析】
根据集合的运算求得,可得,结合图中阴影部分表示的集合为,即可得答案.
【解答】
解:由于全集,,,
故,
则,
故图中阴影部分表示的集合为,
故答案为:
13.【答案】
【解析】【分析】
根据倍角公式即的取值范围从而可求解.
【解答】
解:由题意知,,所以,
所以,,
所以.
故答案为:.
14.【答案】
【解析】【分析】
计算出,函数关于点中心对称,得到有唯一的解,求出函数的单调性,结合题目条件得到,进而得到分段函数解析式,计算出,故,结合函数单调性得到不等式.
【解答】
解:由题意,得,,
所以,即函数关于点中心对称.
因为恒成立,所以当时,,
当时,.
所以有唯一的解.
当时,,函数单调递增,
当时,,函数单调递增,
当时,,函数单调递增,
又,,
故在上单调递增,
,
由对称性可知,
下面证明,过程如下:
若时,则,且,则,,
,
此时,
同理可得当时,,
当,即时,,,满足,即.
故
当时,,
当时,令,解得,
当时,,
又不等式,所以.
由,得由,得.
所以原不等式的解集为.
故答案为:
点睛:函数的对称性:
若,则函数关于中心对称,
若,则函数关于对称
15.【答案】解:函数经过点,
所以,解得,即,
,
则是上的单调递增函数,理由如下:
任取、,且,则,
则,
所以,即,
所以是定义域上的单调递增函数.
因为,
故是奇函数且在上单调递增,
则不等式等价于,
所以,即,
即存在,不等式有解,
即在上有解,
由,可得,
由对勾函数性质易知:在单调递减,在单调递增,
且,故在的最大值为,
所以,即
所以,
即实数的取值范围是.
【解析】由函数经过点求的值,得到的解析式,用定义法证明函数的单调性;
根据函数的奇偶性和单调性,不等式转化为在上有解,利用参数分离法结合基本不等式可求出实数的取值范围.
16.【答案】解:由题意,购买台“机器狗”的总成本为,
则每台机器狗的平均成本为,
当且仅当时,即时,等号成立,
所以,若使每台“机器狗”的平均成本最低,应买台
由题意,“汪”满足,可得,
“汪”满足,可得,
“汪”满足,
,,
所以 ,
因为,,且,
所以可得,
则,
所以,所以“汪”用的时间最少.
【解析】平均成本为,利用比较不等式,即可求解函数的最值;
利用速度,时间和路程的关系,分别求解,,,再根据不等式,比较时间大小,即可求解.
17.【答案】解:以筒车转轮的中心为原点,与水面平行的直线为轴建立平面直角坐标系,
设,,
由题意知,,,
,,即,
当时,,解得,
结合图象初始位置可知,
又因为,所以,
综上,,;
经过后距离水面的高度,
由题意知,
所以经过后距离水面的高度,
则盛水筒与盛水筒的高度差为,
利用,
,
当,,即,时,取最大值,
又因为,所以当或时,取最大值,
综上,盛水筒与盛水筒的高度差的最大值为,此时或.
【解析】本题考查三角函数模型的应用、函数的图象与性质,考查运算求解能力,是较难题.
设,,直接由题意求出,,,的值;
易得,分别求出经过相邻两个盛水筒距离水面的高度,作差后利用三角函数求最值.
18.【答案】解:注射该药品,其浓度为
当时,,解得;
当时,,解得.
所以一次注射该药品,则药物有效时间可达小时.
设从第一次注射起,经小时后,
其浓度,则,
因为,
当时,即时,等号成立.
,当时,,
所以,因为,
解得,所以.
当时,,,所以不能保证持续有效,
答:要使随后的小时内药品能够持续有效治疗,的最小值为.
【解析】由血药浓度与药品在体内时间的关系,计算血药浓度不低于时对应的时间段;
由两次注射的血药浓度之和不低于,利用基本不等式求的最小值.
方法点睛:
分段函数模型的应用:
在现实生活中,很多问题的两变是之间的关系,不能用同一个关系式给出,而是由几个不同的关系式构成分段函数,分段函数模型适用于描述在不同区间上函数值的变化情况,分段函数主要是每一段上自变量变化所遵循的规律不同,可以先将其作为几个不同问题,将各段的规律找出来,再将其合在一起,要注意各段变量的范围,特别是端点.
19.【答案】解:
令,
得
函数的单调递增区间为
令,
则
可得,当即时,;
当即时,
存在,对任意,有恒成立,
为的最小值,为的最大值,
,,
,
.
令,
方程可化为,
令,则,
当时,,,此时函数在上有个零点,
,适合题意;
当时,在内有一解,
在或内有一取值,则此时函数在上有个零点,不适合题意;
当时,,此时函数在上有个零点,
,适合题意;
当时,或,或,则此时函数在上有个零点,不适合题意;
当时,在和内各有一解,在和内各有一取值,
则此时函数在上有个零点,不适合题意;
当时,,,则此时函数在上有个零点,不适合题意.
综上所述,,,或,.
【解析】根据二倍角公式和辅助角公式化简,结合三角函数增区间求法计算即可;
根据题意写出函数,结合平方关系进行换元,结合新元范围与二次函数的知识求解最值,得到,进而得到答案;
将原题意转化为,令,则,再分类讨论进行取舍即可得到答案.
关键点点睛:本题考查三角函数的综合应用问题关键点在于换元法的运用,例如中令,则,进而转化为二次函数;第中方程可化为,令,则,通过换元进而由繁化简进行求解本题考查转化与化归、分类与整合能力,属于难题.
第1页,共1页
同课章节目录
