青岛版九年级数学上册第3章3.2确定圆的条件同步训练题(含答案)
文档属性
| 名称 | 青岛版九年级数学上册第3章3.2确定圆的条件同步训练题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 429.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-27 16:06:04 | ||
图片预览




文档简介
青岛版九年级数学上册第3章3.2确定圆的条件同步训练题(含答案)
一.选择题(共10小题)
1.(2015 江干区二模)给定下列图形可以确定一个圆的是( )
A.已知圆心 B. 已知半径
C.已知直径 D. 不在同一直线上的三个点
2.(2015 丹阳市一模)如图,已知点平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B. (4,5) C. (4,) D. (4,)
(2题图) (3题图) (4题图) (6题图)
3.(2014 武汉模拟)如图,AB=OA=OB=OC,则∠ACB的大小是( )
A.40° B. 30° C. 20° D. 35°
4.(2014秋 宝应县校级期中)如图,点ABC在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个 B. 2个 C. 3个 D. 4个
5.(2014秋 江阴市期中)下列说法正确的有几个( )
①经过三个点一定可以作圆;
②任意一个圆一定有内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个外接圆并且只有一个外接圆;
④垂直于弦的直径必平分弦;
⑤经过不在同一直线上的四个点一定可以作圆.
A.3 B. 2 C. 1 D. 0
6.(2015 湖州模拟)如图,一只花猫发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A,B,C,要想同时顾及这三个出口以防老鼠出洞,这只花猫最好蹲守在( )
A. △ABC的三边高线的交点P处
B. △ABC的三角平分线的交点P处
C. △ABC的三边中线的交点P处
D. △ABC的三边中垂线的交点P处
7.(2015春 安岳县月考)有下列四个命题,其中正确的有( )
①圆的对称轴是直径; ②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.
A. 4个 B. 3个 C. 2个 D. 1个
8.(2015 巴中模拟)若一个三角形的外心在这个三角形的一边上,那么这个三角形是( )
A.锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定
9.(2015 婺城区模拟)如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A. B. C. 2 D.
10.(2014秋 瓯海区校级期中)一个三角形的外接圆的圆心在这个三角形的外部,则该三角形一定是( )
A.锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
(9题图) (13题图) (14题图) (16题图)
二.填空题(共10小题)
11.过平面内一点可以作 个圆,过平面内A、B两点可以作 个圆,圆心在 ,过 只能作一个圆.
12.(2014秋 腾冲县期末)下列说法:①直径是弦;②经过三点一定可以作圆;③三角形的外心到三角形各顶点的距离相等;④长度相等的弧是等弧;⑤平分弦的直径垂直于弦.其中正确的是 (填序号).
13.(2015春 清河区校级期末)如图△ABC中外接圆的圆心坐标是 .
14.(2015 江西模拟)平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是 .
15.(2015 岳池县模拟)直角三角形的两直角边分别3,4;则它的外接圆半径R= .
16.(2015 高淳县二模)如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 .
17.(2015春 兴化市校级期末)直角三角形的两边是6和8,则它的外接圆的直径为 .
18.(2014秋 沈阳期中)如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在 .
(18题图) (20题图)
19.(2014秋 江都市校级月考)已知三角形三边长分别为1cm、cm和cm,则此三角形的外接圆半径为 cm.
20.(2015春 潜山县校级月考)如图,△ABC的外接圆的圆心坐标是 .
三.解答题(共5小题)
21.(2015 上城区校级模拟)平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是 .
22.(2015 扬州模拟)如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
23.(2015春 贺兰县校级月考)作图题:
(1)分别作出点P,使得PA=PB=PC;
(2)观察各图中的点P与△ABC的位置关系,并总结规律:
当△ABC为锐角三角形时,点P在△ABC的 ;
当△ABC为直角三角形时,点P在△ABC的 ;
当△ABC为钝角三角形时,点P在△ABC的 ;反之也成立,且在平面内到三角形各顶点距离相等的点只有一个.
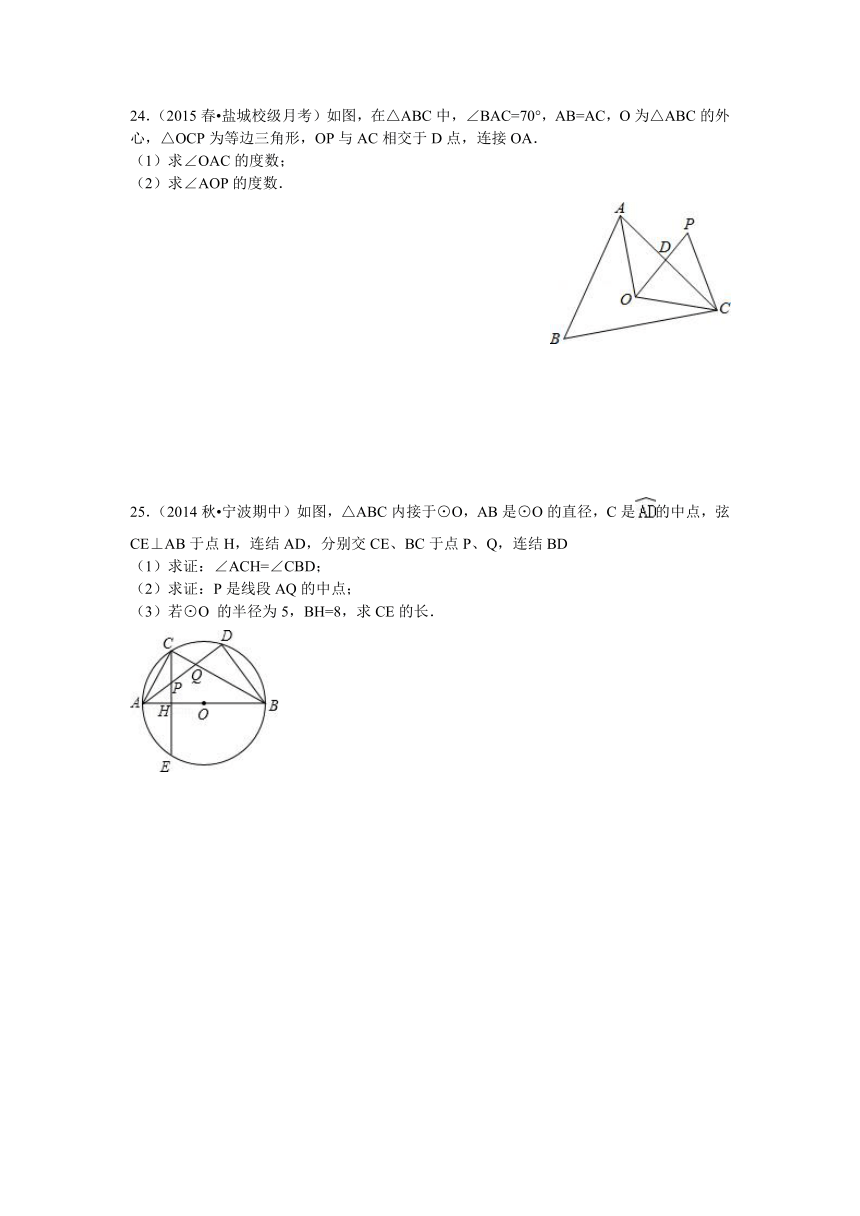
24.(2015春 盐城校级月考)如图,在△ABC中,∠BAC=70°,AB=AC,O为△ABC的外心,△OCP为等边三角形,OP与AC相交于D点,连接OA.
(1)求∠OAC的度数;
(2)求∠AOP的度数.
25.(2014秋 宁波期中)如图,△ABC内接于⊙O,AB是⊙O的直径,C是的中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD
(1)求证:∠ACH=∠CBD;
(2)求证:P是线段AQ的中点;
(3)若⊙O 的半径为5,BH=8,求CE的长.
青岛版九年级数学上册第3章3.2确定圆的条件同步训练题参考答案
一.选择题(共10小题)
1.D 2.C 3.B 4.C 5.C 6.D 7.C 8.B 9.A 10.C
二.填空题(共10小题)
11.无数无数AB的垂直平分线上不在同一直线上的三点 12.①③ 13.(6,2)
14.(6,6) 15.2.5 16.(2,1) 17.10或8
18.三角形ABC的两边的垂直平分线的交点上 19. 20.(-2,-1)
三.解答题(共5小题)
21.解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,
因而交点P的坐标是(6,6).
(21题图) (22题图)
22.解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
答:圆的半径为13cm.
23.解:(1)如图所示:分别作出三角形任意两边垂直平分线,
根据垂直平分线的性质,可得两直线的交点,即是P点.
(2)结合图象可知:
故填:内部;斜边的中点;外部
24.解:∵O为△ABC的外心,∠BAC=70°,AB=AC,
∴∠OAC=35°(AO垂直平分BC,则三线合一),
(2)∵O为△ABC的外心,∴AO=CO,∴∠OAC=∠OCA=35°,∴∠AOC=110°,
∵△OCP为正三角形,∴∠AOP=50°.
25.(1)证明:∵AB是⊙O的直径,CE⊥AB,∴AB垂直平分CE,
即H为CE中点,弧AC=弧AE
又∵C是的中点,∴弧AC=弧CD∴弧AC=弧CD=弧AE∴∠ACH=∠CBD;
(2)由(1)知,∠ACH=∠CBD,
又∵∠CAD=∠CBD
∴∠ACH=∠CAD,
∴AP=CP
又∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∴∠PCQ=90°﹣∠ACH,∠PQC=∠BQD=90°﹣∠CBD,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,
即P是线段AQ的中点;
(3)解:连接OC,
∵BH=8,OB=OC=5,
∴OH=3
∴由勾股定理得:CH==4
由(1)知:CH=EH=4,
∴CE=8.
鲁教版六年级数学下册第8章8.4统计图的选择同步训练题(含答案)
一.选择题(共10小题)
1.(2015 贵阳模拟)小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
A. 阅读数量的平均数是57 B. 阅读数量的众数是42
C. 阅读数量的中位数是58 D. 有4个月的阅读数量超过60本
(1题图) (5题图)
2.(2015 杭州)如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中PM2.5浓度的中位数是112ug/m3;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是( )
A.①②③ B. ①②④ C. ①③④ D. ②③④
3.(2015 福州)下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B. 条形图 C. 折线图 D. 直方图
4.(2015春 嘉兴期末)要反映嘉兴市一天内气温的变化情况宜采用( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.频数分布直方图
5.(2015 杭州模拟)如图,是杭州PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
A.表示汽车尾气排放的圆心角约72° B.表示建筑扬尘的占6%
C.煤炭以及其他燃料燃放约为建筑扬尘的5倍 D.汽车尾气排放影响最大
6.(2014秋 东平县期末)李老师对本班50名学生的血型作了统计,列出如下的统计表,则本班AB型血的人数是( )
组别 A型 B型 AB型 O型
占全班人数的百分比 40% 30% 20% 10%
A.20人 B. 15人 C. 5人 D. 10人
7.(2015 扬州)如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )
A.音乐组 B. 美术组 C. 体育组 D. 科技组
(7题图) (8题图) (10题图)
8.(2015 邵阳)如图是某校参加各兴趣小组的学生人数分布扇形统计图,则参加人数最多的兴趣小组是( )
A.棋类 B. 书画 C. 球类 D. 演艺
9.(2015 恩施州)某中学开展“阳光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
A.240 B. 120 C. 80 D. 40
10.(2015 路北区一模)如图所示是甲、乙两户居民家庭全年各项支出的统计图.根据统计图,下列对两户居民家庭教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大 B.乙户比甲户大
C.甲、乙两户一样大 D.无法确定哪一户大
二.填空题(共10小题)
11.(2015春 南昌期末)下表是我市某一天在不同时段测得的气温情况:则这一天的气温的温差是 ℃,温度最接近的两个时间是 与 .
0:00 4:00 8:00 12:00 16:00 20:00
25℃ 27℃ 29℃ 32℃ 34℃ 30℃
12.(2014秋 围场县校级期末)已知全班有40位学生,他们有的步行,有的骑车,还有的乘车来上学,根据以下已知信息完成统计表:
上学方式 步行 骑车 乘车
划计 正正正
次数 9
占百分比
13.(2015 苏州)某学校“你最喜爱的球类运动”调查中,随机调查了若干名学生(每个学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人,则该校被调查的学生总人数为 名.
(13题图) (14题图) (15题图)
14.(2015 玉林)某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是 .
15.(2015 黄浦区二模)某校八年级共四个班,各班寒假外出旅游的学生人数如图所示,那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为 .
16.(2015春 和平区期末)七年级(1)班在一次数学抽测中某道选择题的答题情况如图(1),(2)所示.根据统计图可得选A的有 人,选B的有 人,选C的有 人.
(16题图) (17题图)
17.(2015 通州区一模)生物学研究表明在8﹣17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是 岁,在 岁时男生女生的身高增长速度是一样的.
18.(2015春 南昌期末)如图是小浩同学8月1日 7日毎天的自主学习时间统计图,则小浩同学一天中自主学习时间最长是 小时,这七天平均每天的自主学习时间是 小时.
19.(2015春 大冶市期末)空气中由多种气体混合而成,为了简明扼要地介绍空气的组成情况,较好地描述空气中各种成分所占的百分比,最适合采用的统计图是 统计图.
20.(2015春 沭阳县期中)某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.
三.解答题(共5小题)
21.(2015 绵阳模拟)某中学在“五月份学习竞赛月”中举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 90 60 15
比例(%) 12 25 20 8 5
认真阅读统计图表后,回答下列问题:
(1)请补充完成统计表;
(2)本次参加比赛的总人数是 人,本次比赛项目的众数是 .
(3)根据上述数据,你可以获得什么信息.
22.(2015 酒泉)某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
进球数(个) 8 7 6 5 4 3
人数 2 1 4 7 8 2
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;
(2)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
23.(2015 自贡)在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
24.(2015 遂宁)交通指数是交通拥堵指数的简称,是综合反映道路畅通或拥堵的概念.其指数在100以内为畅通,200以上为严重拥堵,从某市交通指挥中心选取了5月1日至14日的交通状况,依据交通指数数据绘制的折线统计图如图所示,某人随机选取了5月1日至14日的某一天到达该市.
(1)请结合折线图分别找出交通为畅通和严重拥堵的天数;
(2)求此人到达当天的交通为严重拥堵的概率;
(3)由图判断从哪天开始连续三天的交通指数方差最大?(直接判断,不要求计算)
25.(2015 大连)某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 测试成绩(分) 人数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有 人,达到优秀的人数占本次测试总人数的百分比为 %.
(2)本次测试的学生数为 人,其中,体质健康成绩为及格的有 人,不及格的人数占本次测试总人数的百分比为 %.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
鲁教版六年级数学下册第8章8.4统计图的选择同步训练题参考答案
一.选择题(共10小题)
1.C 2.C 3.A 4.C 5.D6.D 7.C 8.C 9.D 10.B
二.填空题(共10小题)
11.9 8:00 0:00 12.37.5% 22.5% 40% 13.60 14.40% 15.40%
16.8 4 28 17.13 11 18.3 1.5 19.扇形 20.折线
三.解答题(共5小题)
21.解:(1)参赛的总人数是:60÷20%=300(人),
则参加书法的人数是:300×25%=75(人),
参加作文比赛的比例是:×100%=30%,
参加小品比赛的人数是:300×8%=24(人);
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 75 90 60 24 15
比例(%) 12 25 30 20 8 5
(2)参赛的总人数是300,本次比赛项目的众数是作文.
故答案是:300,作文;
(3)可以获得什么信息是:学生比较喜欢作文和书法.
22.解:(1)参加篮球训练的人数是:2+1+4+7+8+2=24(人).
训练后篮球定时定点投篮人均进球数==5(个).
故答案是:5;
(2)由扇形图可以看出:选择长跑训练的人数占全班人数的百分比=1﹣60%﹣10%﹣20%=10%,
则全班同学的人数为24÷60%=40(人),
故答案是:10%,40;
(3)设参加训练之前的人均进球数为x个,
则x(1+25%)=5,解得 x=4.
即参加训练之前的人均进球数是4个.
23.解:(1)(1﹣45%﹣5%﹣40%)×360°=36°;
(2)380×45%﹣67﹣44=60;
60﹣18﹣13﹣12﹣3=14;
(3)依题意,得45%×60=27,
答:唐老师应安排27课时复习“数与代数”内容.
故答案为:36,60,14.
24.解:(1)由纵坐标看出畅通的天数为7天,严重拥堵的天数为2天;
(2)此人到达当天的交通为严重拥堵的概率p==;
(3)由方差越大,数据波动越大,得
5、6、7三天数据波动大.
25.解:(1)本次测试学生体质健康成绩为良好的有36人.
达到优秀的人数占本次测试总人数的百分比为70%.
故答案是:36,70;
(2)调查的总人数是:140÷70%=200(人),
体质健康成绩为及格的有200﹣140﹣36﹣6=18(人),
不及格的人数占本次测试总人数的百分比是:×100%=3%.
故答案是:200,18,3%;
(3)本次测试学生体质健康成绩为良好的有36人,=18%,
估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数是:1800×(70%+18%)=1584(人).
一.选择题(共10小题)
1.(2015 江干区二模)给定下列图形可以确定一个圆的是( )
A.已知圆心 B. 已知半径
C.已知直径 D. 不在同一直线上的三个点
2.(2015 丹阳市一模)如图,已知点平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B. (4,5) C. (4,) D. (4,)
(2题图) (3题图) (4题图) (6题图)
3.(2014 武汉模拟)如图,AB=OA=OB=OC,则∠ACB的大小是( )
A.40° B. 30° C. 20° D. 35°
4.(2014秋 宝应县校级期中)如图,点ABC在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个 B. 2个 C. 3个 D. 4个
5.(2014秋 江阴市期中)下列说法正确的有几个( )
①经过三个点一定可以作圆;
②任意一个圆一定有内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个外接圆并且只有一个外接圆;
④垂直于弦的直径必平分弦;
⑤经过不在同一直线上的四个点一定可以作圆.
A.3 B. 2 C. 1 D. 0
6.(2015 湖州模拟)如图,一只花猫发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A,B,C,要想同时顾及这三个出口以防老鼠出洞,这只花猫最好蹲守在( )
A. △ABC的三边高线的交点P处
B. △ABC的三角平分线的交点P处
C. △ABC的三边中线的交点P处
D. △ABC的三边中垂线的交点P处
7.(2015春 安岳县月考)有下列四个命题,其中正确的有( )
①圆的对称轴是直径; ②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.
A. 4个 B. 3个 C. 2个 D. 1个
8.(2015 巴中模拟)若一个三角形的外心在这个三角形的一边上,那么这个三角形是( )
A.锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定
9.(2015 婺城区模拟)如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A. B. C. 2 D.
10.(2014秋 瓯海区校级期中)一个三角形的外接圆的圆心在这个三角形的外部,则该三角形一定是( )
A.锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
(9题图) (13题图) (14题图) (16题图)
二.填空题(共10小题)
11.过平面内一点可以作 个圆,过平面内A、B两点可以作 个圆,圆心在 ,过 只能作一个圆.
12.(2014秋 腾冲县期末)下列说法:①直径是弦;②经过三点一定可以作圆;③三角形的外心到三角形各顶点的距离相等;④长度相等的弧是等弧;⑤平分弦的直径垂直于弦.其中正确的是 (填序号).
13.(2015春 清河区校级期末)如图△ABC中外接圆的圆心坐标是 .
14.(2015 江西模拟)平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是 .
15.(2015 岳池县模拟)直角三角形的两直角边分别3,4;则它的外接圆半径R= .
16.(2015 高淳县二模)如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 .
17.(2015春 兴化市校级期末)直角三角形的两边是6和8,则它的外接圆的直径为 .
18.(2014秋 沈阳期中)如图,A,B,C三个居民小区在位置上成三角形,现决定在三个小区之间修建一个购物超市,若超市到三个小区的距离相等,则超市应建在 .
(18题图) (20题图)
19.(2014秋 江都市校级月考)已知三角形三边长分别为1cm、cm和cm,则此三角形的外接圆半径为 cm.
20.(2015春 潜山县校级月考)如图,△ABC的外接圆的圆心坐标是 .
三.解答题(共5小题)
21.(2015 上城区校级模拟)平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是 .
22.(2015 扬州模拟)如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
23.(2015春 贺兰县校级月考)作图题:
(1)分别作出点P,使得PA=PB=PC;
(2)观察各图中的点P与△ABC的位置关系,并总结规律:
当△ABC为锐角三角形时,点P在△ABC的 ;
当△ABC为直角三角形时,点P在△ABC的 ;
当△ABC为钝角三角形时,点P在△ABC的 ;反之也成立,且在平面内到三角形各顶点距离相等的点只有一个.
24.(2015春 盐城校级月考)如图,在△ABC中,∠BAC=70°,AB=AC,O为△ABC的外心,△OCP为等边三角形,OP与AC相交于D点,连接OA.
(1)求∠OAC的度数;
(2)求∠AOP的度数.
25.(2014秋 宁波期中)如图,△ABC内接于⊙O,AB是⊙O的直径,C是的中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD
(1)求证:∠ACH=∠CBD;
(2)求证:P是线段AQ的中点;
(3)若⊙O 的半径为5,BH=8,求CE的长.
青岛版九年级数学上册第3章3.2确定圆的条件同步训练题参考答案
一.选择题(共10小题)
1.D 2.C 3.B 4.C 5.C 6.D 7.C 8.B 9.A 10.C
二.填空题(共10小题)
11.无数无数AB的垂直平分线上不在同一直线上的三点 12.①③ 13.(6,2)
14.(6,6) 15.2.5 16.(2,1) 17.10或8
18.三角形ABC的两边的垂直平分线的交点上 19. 20.(-2,-1)
三.解答题(共5小题)
21.解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,
因而交点P的坐标是(6,6).
(21题图) (22题图)
22.解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
答:圆的半径为13cm.
23.解:(1)如图所示:分别作出三角形任意两边垂直平分线,
根据垂直平分线的性质,可得两直线的交点,即是P点.
(2)结合图象可知:
故填:内部;斜边的中点;外部
24.解:∵O为△ABC的外心,∠BAC=70°,AB=AC,
∴∠OAC=35°(AO垂直平分BC,则三线合一),
(2)∵O为△ABC的外心,∴AO=CO,∴∠OAC=∠OCA=35°,∴∠AOC=110°,
∵△OCP为正三角形,∴∠AOP=50°.
25.(1)证明:∵AB是⊙O的直径,CE⊥AB,∴AB垂直平分CE,
即H为CE中点,弧AC=弧AE
又∵C是的中点,∴弧AC=弧CD∴弧AC=弧CD=弧AE∴∠ACH=∠CBD;
(2)由(1)知,∠ACH=∠CBD,
又∵∠CAD=∠CBD
∴∠ACH=∠CAD,
∴AP=CP
又∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∴∠PCQ=90°﹣∠ACH,∠PQC=∠BQD=90°﹣∠CBD,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,
即P是线段AQ的中点;
(3)解:连接OC,
∵BH=8,OB=OC=5,
∴OH=3
∴由勾股定理得:CH==4
由(1)知:CH=EH=4,
∴CE=8.
鲁教版六年级数学下册第8章8.4统计图的选择同步训练题(含答案)
一.选择题(共10小题)
1.(2015 贵阳模拟)小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
A. 阅读数量的平均数是57 B. 阅读数量的众数是42
C. 阅读数量的中位数是58 D. 有4个月的阅读数量超过60本
(1题图) (5题图)
2.(2015 杭州)如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中PM2.5浓度的中位数是112ug/m3;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是( )
A.①②③ B. ①②④ C. ①③④ D. ②③④
3.(2015 福州)下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B. 条形图 C. 折线图 D. 直方图
4.(2015春 嘉兴期末)要反映嘉兴市一天内气温的变化情况宜采用( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.频数分布直方图
5.(2015 杭州模拟)如图,是杭州PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
A.表示汽车尾气排放的圆心角约72° B.表示建筑扬尘的占6%
C.煤炭以及其他燃料燃放约为建筑扬尘的5倍 D.汽车尾气排放影响最大
6.(2014秋 东平县期末)李老师对本班50名学生的血型作了统计,列出如下的统计表,则本班AB型血的人数是( )
组别 A型 B型 AB型 O型
占全班人数的百分比 40% 30% 20% 10%
A.20人 B. 15人 C. 5人 D. 10人
7.(2015 扬州)如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )
A.音乐组 B. 美术组 C. 体育组 D. 科技组
(7题图) (8题图) (10题图)
8.(2015 邵阳)如图是某校参加各兴趣小组的学生人数分布扇形统计图,则参加人数最多的兴趣小组是( )
A.棋类 B. 书画 C. 球类 D. 演艺
9.(2015 恩施州)某中学开展“阳光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
A.240 B. 120 C. 80 D. 40
10.(2015 路北区一模)如图所示是甲、乙两户居民家庭全年各项支出的统计图.根据统计图,下列对两户居民家庭教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大 B.乙户比甲户大
C.甲、乙两户一样大 D.无法确定哪一户大
二.填空题(共10小题)
11.(2015春 南昌期末)下表是我市某一天在不同时段测得的气温情况:则这一天的气温的温差是 ℃,温度最接近的两个时间是 与 .
0:00 4:00 8:00 12:00 16:00 20:00
25℃ 27℃ 29℃ 32℃ 34℃ 30℃
12.(2014秋 围场县校级期末)已知全班有40位学生,他们有的步行,有的骑车,还有的乘车来上学,根据以下已知信息完成统计表:
上学方式 步行 骑车 乘车
划计 正正正
次数 9
占百分比
13.(2015 苏州)某学校“你最喜爱的球类运动”调查中,随机调查了若干名学生(每个学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人,则该校被调查的学生总人数为 名.
(13题图) (14题图) (15题图)
14.(2015 玉林)某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是 .
15.(2015 黄浦区二模)某校八年级共四个班,各班寒假外出旅游的学生人数如图所示,那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为 .
16.(2015春 和平区期末)七年级(1)班在一次数学抽测中某道选择题的答题情况如图(1),(2)所示.根据统计图可得选A的有 人,选B的有 人,选C的有 人.
(16题图) (17题图)
17.(2015 通州区一模)生物学研究表明在8﹣17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是 岁,在 岁时男生女生的身高增长速度是一样的.
18.(2015春 南昌期末)如图是小浩同学8月1日 7日毎天的自主学习时间统计图,则小浩同学一天中自主学习时间最长是 小时,这七天平均每天的自主学习时间是 小时.
19.(2015春 大冶市期末)空气中由多种气体混合而成,为了简明扼要地介绍空气的组成情况,较好地描述空气中各种成分所占的百分比,最适合采用的统计图是 统计图.
20.(2015春 沭阳县期中)某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.
三.解答题(共5小题)
21.(2015 绵阳模拟)某中学在“五月份学习竞赛月”中举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 90 60 15
比例(%) 12 25 20 8 5
认真阅读统计图表后,回答下列问题:
(1)请补充完成统计表;
(2)本次参加比赛的总人数是 人,本次比赛项目的众数是 .
(3)根据上述数据,你可以获得什么信息.
22.(2015 酒泉)某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
进球数(个) 8 7 6 5 4 3
人数 2 1 4 7 8 2
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;
(2)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
23.(2015 自贡)在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
24.(2015 遂宁)交通指数是交通拥堵指数的简称,是综合反映道路畅通或拥堵的概念.其指数在100以内为畅通,200以上为严重拥堵,从某市交通指挥中心选取了5月1日至14日的交通状况,依据交通指数数据绘制的折线统计图如图所示,某人随机选取了5月1日至14日的某一天到达该市.
(1)请结合折线图分别找出交通为畅通和严重拥堵的天数;
(2)求此人到达当天的交通为严重拥堵的概率;
(3)由图判断从哪天开始连续三天的交通指数方差最大?(直接判断,不要求计算)
25.(2015 大连)某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 测试成绩(分) 人数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有 人,达到优秀的人数占本次测试总人数的百分比为 %.
(2)本次测试的学生数为 人,其中,体质健康成绩为及格的有 人,不及格的人数占本次测试总人数的百分比为 %.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
鲁教版六年级数学下册第8章8.4统计图的选择同步训练题参考答案
一.选择题(共10小题)
1.C 2.C 3.A 4.C 5.D6.D 7.C 8.C 9.D 10.B
二.填空题(共10小题)
11.9 8:00 0:00 12.37.5% 22.5% 40% 13.60 14.40% 15.40%
16.8 4 28 17.13 11 18.3 1.5 19.扇形 20.折线
三.解答题(共5小题)
21.解:(1)参赛的总人数是:60÷20%=300(人),
则参加书法的人数是:300×25%=75(人),
参加作文比赛的比例是:×100%=30%,
参加小品比赛的人数是:300×8%=24(人);
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 75 90 60 24 15
比例(%) 12 25 30 20 8 5
(2)参赛的总人数是300,本次比赛项目的众数是作文.
故答案是:300,作文;
(3)可以获得什么信息是:学生比较喜欢作文和书法.
22.解:(1)参加篮球训练的人数是:2+1+4+7+8+2=24(人).
训练后篮球定时定点投篮人均进球数==5(个).
故答案是:5;
(2)由扇形图可以看出:选择长跑训练的人数占全班人数的百分比=1﹣60%﹣10%﹣20%=10%,
则全班同学的人数为24÷60%=40(人),
故答案是:10%,40;
(3)设参加训练之前的人均进球数为x个,
则x(1+25%)=5,解得 x=4.
即参加训练之前的人均进球数是4个.
23.解:(1)(1﹣45%﹣5%﹣40%)×360°=36°;
(2)380×45%﹣67﹣44=60;
60﹣18﹣13﹣12﹣3=14;
(3)依题意,得45%×60=27,
答:唐老师应安排27课时复习“数与代数”内容.
故答案为:36,60,14.
24.解:(1)由纵坐标看出畅通的天数为7天,严重拥堵的天数为2天;
(2)此人到达当天的交通为严重拥堵的概率p==;
(3)由方差越大,数据波动越大,得
5、6、7三天数据波动大.
25.解:(1)本次测试学生体质健康成绩为良好的有36人.
达到优秀的人数占本次测试总人数的百分比为70%.
故答案是:36,70;
(2)调查的总人数是:140÷70%=200(人),
体质健康成绩为及格的有200﹣140﹣36﹣6=18(人),
不及格的人数占本次测试总人数的百分比是:×100%=3%.
故答案是:200,18,3%;
(3)本次测试学生体质健康成绩为良好的有36人,=18%,
估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数是:1800×(70%+18%)=1584(人).
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
