青岛版七年级数学下册第13章13.2多边形同步训练题(含答案)
文档属性
| 名称 | 青岛版七年级数学下册第13章13.2多边形同步训练题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 382.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-27 16:06:48 | ||
图片预览


文档简介
青岛版七年级数学下册第13章13.2多边形同步训练题(含答案)
一.选择题(共11小题)
1.(2013秋 太康县期末)下列图形中,多边形有( )
A.1个 B. 2个 C. 3个 D. 4个
2.(2015春 东平县校级月考)七边形的对角线共有( )
A.10条 B. 15条 C. 21条 D. 14条
3.(2015春 张家港市期末)从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是( )
A.6 B. 7 C. 8 D. 9
4.(2014秋 朝阳区期末)在六边形内任取一点,把这个点与六边形的各顶点分别连接可以得到( )
A.4个三角形 B. 5个三角形 C. 6个三角形 D. 7个三角形
5.(2015春 郑州期末)过多边形某个顶点的所有对角线,将这个多边形分成7个三角形,这个多边形是( )
A.八边形 B. 九边形 C. 十边形 D. 十一边形
6.(2015 重庆校级模拟)如图,正四边形有2条对角线,正五边形有5条对角线,正六边形有9条对角线,则正十边形有( )条对角线.
A.27 B. 35 C. 40 D. 44
7.(2015 无锡)八边形的内角和为( )
A.180° B. 360° C. 1080° D. 1440°
8.(2015 孝感)已知一个正多边形的每个外角等于60°,则这个正多边形是( )
A.正五边形 B. 正六边形 C. 正七边形 D. 正八边形
9.(2015 大庆)正n边形每个内角的大小都为108°,则n=( )
A.5 B. 6 C. 7 D. 8
10.(2015 宿迁)已知一个多边形的内角和等于它的外角和,则这个多边形的边数为( )
A.3 B. 4 C. 5 D. 6
11.(2015 莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
A.27 B. 35 C. 44 D. 54
二.填空题(共8小题)
12.(2014秋 吉州区期末)十边形有 个顶点,从一个顶点出发可画 条对角线,它共有 条对角线.
13.(2015春 海淀区校级期末)若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是 边形.
14.(2014秋 郸城县校级月考)一个四边形截去一个角后变成 .
15.(2015 辽阳)一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
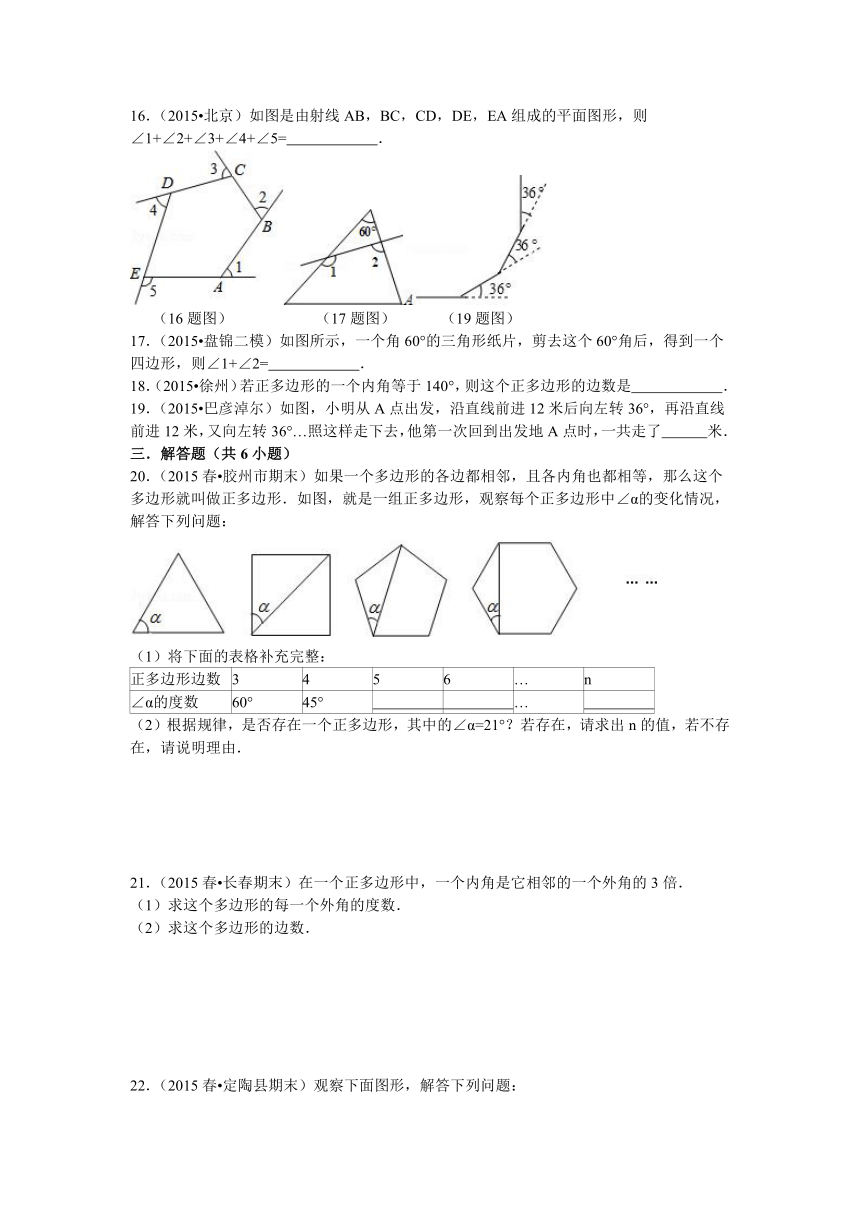
16.(2015 北京)如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= .
(16题图) (17题图) (19题图)
17.(2015 盘锦二模)如图所示,一个角60°的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2= .
18.(2015 徐州)若正多边形的一个内角等于140°,则这个正多边形的边数是 .
19.(2015 巴彦淖尔)如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了 米.
三.解答题(共6小题)
20.(2015春 胶州市期末)如果一个多边形的各边都相邻,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° …
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
21.(2015春 长春期末)在一个正多边形中,一个内角是它相邻的一个外角的3倍.
(1)求这个多边形的每一个外角的度数.
(2)求这个多边形的边数.
22.(2015春 定陶县期末)观察下面图形,解答下列问题:
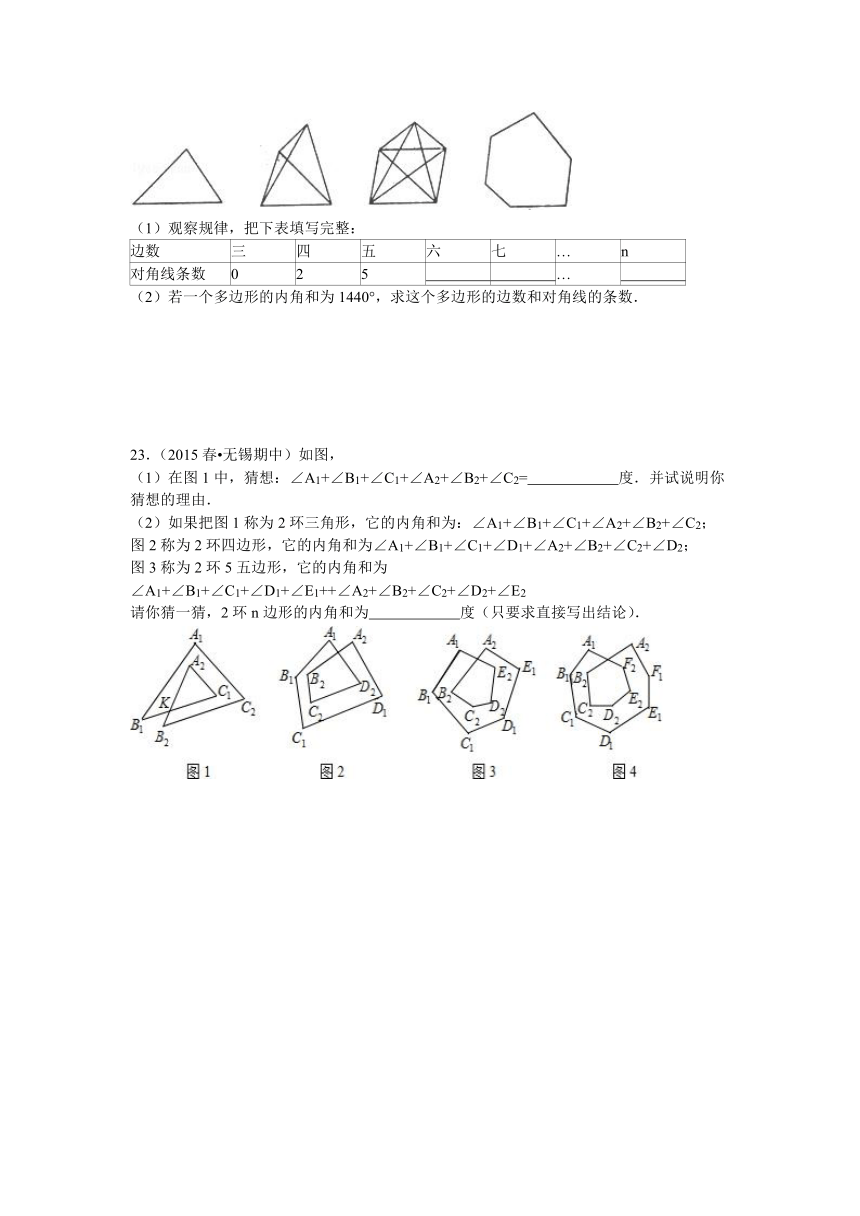
(1)观察规律,把下表填写完整:
边数 三 四 五 六 七 … n
对角线条数 0 2 5 …
(2)若一个多边形的内角和为1440°,求这个多边形的边数和对角线的条数.
23.(2015春 无锡期中)如图,
(1)在图1中,猜想:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2= 度.并试说明你猜想的理由.
(2)如果把图1称为2环三角形,它的内角和为:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2称为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1++∠A2+∠B2+∠C2+∠D2+∠E2
请你猜一猜,2环n边形的内角和为 度(只要求直接写出结论).
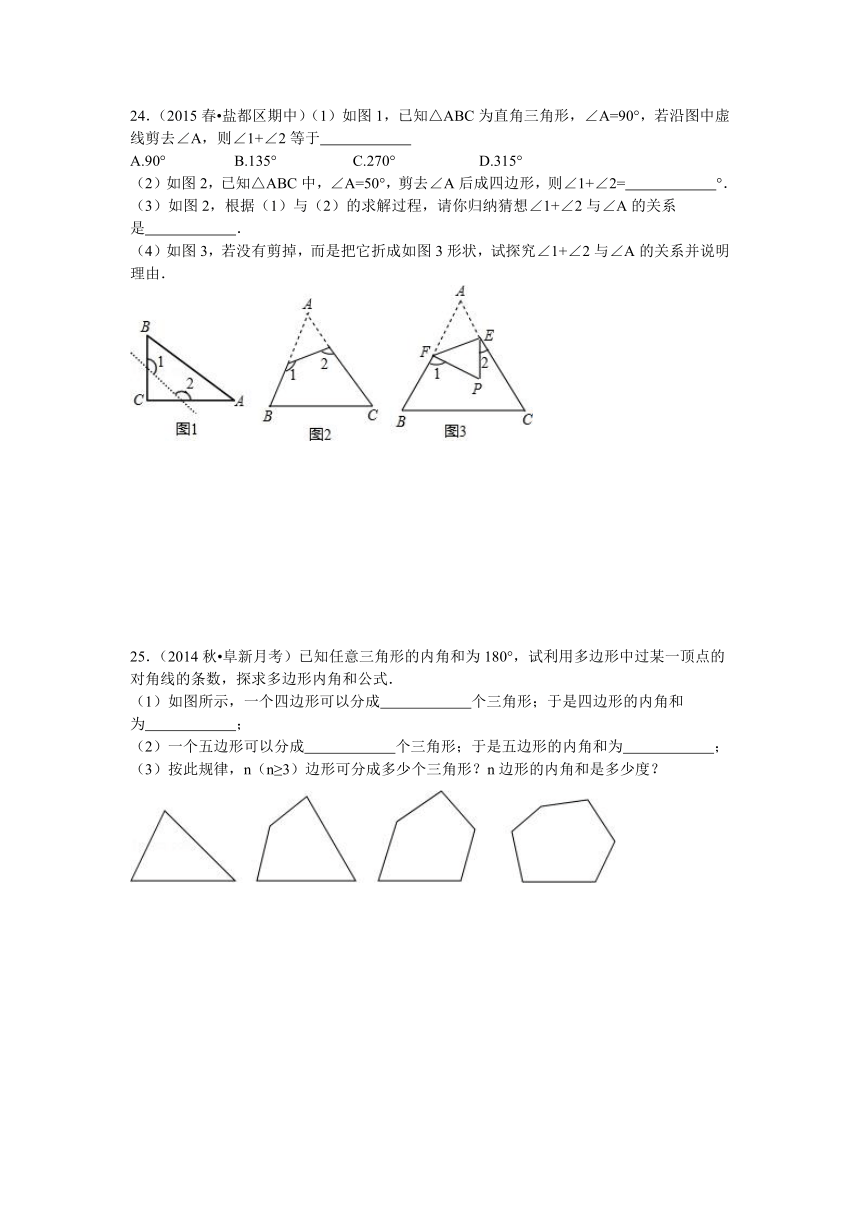
24.(2015春 盐都区期中)(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于
A.90° B.135° C.270° D.315°
(2)如图2,已知△ABC中,∠A=50°,剪去∠A后成四边形,则∠1+∠2= °.
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是 .
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
25.(2014秋 阜新月考)已知任意三角形的内角和为180°,试利用多边形中过某一顶点的对角线的条数,探求多边形内角和公式.
(1)如图所示,一个四边形可以分成 个三角形;于是四边形的内角和为 ;
(2)一个五边形可以分成 个三角形;于是五边形的内角和为 ;
(3)按此规律,n(n≥3)边形可分成多少个三角形?n边形的内角和是多少度?
青岛版七年级数学下册第13章13.2多边形同步训练题参考答案
一.选择题(共11小题)
1.B 2.D 3.C 4.C 5.B 6.B 7.C 8.B
9.A 10.B 11.C
二.填空题(共8小题)
12.10 7 35 13.13 14.三角形或四边形或五边形 15.6
16.360° 17.240° 18.9 19.120
三.解答题(共6小题)
20.解:(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° 36° 30° … ()°
(3)不存在,理由如下:
设存在正n边形使得∠α=21°,
得∠α=21°=()°.
解得:n=8,n是正整数,n=8(不符合题意要舍去),
不存在正n边形使得∠α=21°.
21.解:(1)设这个多边形的每一个外角的度数为x度.根据题意,得:
3x+x=180,
解得x=45.
故这个多边形的每一个外角的度数为45°;
(2)360°÷45°=8.
故这个多边形的边数为8.
22.解:(1)
边数 三 四 五 六 七 … n
对角线条数 0 2 5 9 14 …
(2)设多边形的边数为n.
则(n﹣2)×180=1440,解得n=10.
∴对角线的条数为:=35(条).
故答案为9,14,.
23.解:(1)连结B1B2,
则∠A2+∠C1=∠B1B2A2+∠B2B1C1,
∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=∠A1+∠B1+∠B1B2A2+∠B2B1C1+∠B2+∠C2=360度;
(2)如图,A1A2之间添加两条边,
可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2则∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2=∠A1+∠B1+∠C1+∠D1+∠A2+∠EA1D+∠A1EA2+∠EA2B2=720°;
2环n边形添加(n﹣2)条边,2环n边形的内角和成为(2n﹣2)边形的内角和.其内角和为180(2n﹣4)=360(n﹣2)度.
故答案为:(1)360;(2)360(n﹣2)
24.解:(1)∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2等于270°.
故选C;
(2)∠1+∠2=180°+50°=230°.
故答案是:230;
(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;
故答案是:∠1+∠2=180°+∠A;
(4)∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF
∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF
∴∠1+∠2=360°﹣2(∠AFE+∠AEF)
又∵∠AFE+∠AEF=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A,
即∠1+∠2=2∠A.
25.解:(1)∵四边形可分为两个三角形,
∴四边形的内角和=180°×2=360°.
故答案为:2,360°;
(2))∵五边形可分为三个三角形,
∴四边形的内角和=180°×3=540°.
故答案为:3,540°;
(3)由(1)、(2)可知,过n边形一个顶点的对角线将n边形可以分成(n﹣2)个三角形,于是n边形的内角和为(n﹣2) 180°.
故答案为:n﹣2,(n﹣2) 180°.
鲁教版六年级数学下册第8章8.4统计图的选择同步训练题(含答案)
一.选择题(共10小题)
1.(2015 贵阳模拟)小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
A. 阅读数量的平均数是57 B. 阅读数量的众数是42
C. 阅读数量的中位数是58 D. 有4个月的阅读数量超过60本
(1题图) (5题图)
2.(2015 杭州)如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中PM2.5浓度的中位数是112ug/m3;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是( )
A.①②③ B. ①②④ C. ①③④ D. ②③④
3.(2015 福州)下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B. 条形图 C. 折线图 D. 直方图
4.(2015春 嘉兴期末)要反映嘉兴市一天内气温的变化情况宜采用( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.频数分布直方图
5.(2015 杭州模拟)如图,是杭州PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
A.表示汽车尾气排放的圆心角约72° B.表示建筑扬尘的占6%
C.煤炭以及其他燃料燃放约为建筑扬尘的5倍 D.汽车尾气排放影响最大
6.(2014秋 东平县期末)李老师对本班50名学生的血型作了统计,列出如下的统计表,则本班AB型血的人数是( )
组别 A型 B型 AB型 O型
占全班人数的百分比 40% 30% 20% 10%
A.20人 B. 15人 C. 5人 D. 10人
7.(2015 扬州)如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )
A.音乐组 B. 美术组 C. 体育组 D. 科技组
(7题图) (8题图) (10题图)
8.(2015 邵阳)如图是某校参加各兴趣小组的学生人数分布扇形统计图,则参加人数最多的兴趣小组是( )
A.棋类 B. 书画 C. 球类 D. 演艺
9.(2015 恩施州)某中学开展“阳光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
A.240 B. 120 C. 80 D. 40
10.(2015 路北区一模)如图所示是甲、乙两户居民家庭全年各项支出的统计图.根据统计图,下列对两户居民家庭教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大 B.乙户比甲户大
C.甲、乙两户一样大 D.无法确定哪一户大
二.填空题(共10小题)
11.(2015春 南昌期末)下表是我市某一天在不同时段测得的气温情况:则这一天的气温的温差是 ℃,温度最接近的两个时间是 与 .
0:00 4:00 8:00 12:00 16:00 20:00
25℃ 27℃ 29℃ 32℃ 34℃ 30℃
12.(2014秋 围场县校级期末)已知全班有40位学生,他们有的步行,有的骑车,还有的乘车来上学,根据以下已知信息完成统计表:
上学方式 步行 骑车 乘车
划计 正正正
次数 9
占百分比
13.(2015 苏州)某学校“你最喜爱的球类运动”调查中,随机调查了若干名学生(每个学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人,则该校被调查的学生总人数为 名.
(13题图) (14题图) (15题图)
14.(2015 玉林)某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是 .
15.(2015 黄浦区二模)某校八年级共四个班,各班寒假外出旅游的学生人数如图所示,那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为 .
16.(2015春 和平区期末)七年级(1)班在一次数学抽测中某道选择题的答题情况如图(1),(2)所示.根据统计图可得选A的有 人,选B的有 人,选C的有 人.
(16题图) (17题图)
17.(2015 通州区一模)生物学研究表明在8﹣17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是 岁,在 岁时男生女生的身高增长速度是一样的.
18.(2015春 南昌期末)如图是小浩同学8月1日 7日毎天的自主学习时间统计图,则小浩同学一天中自主学习时间最长是 小时,这七天平均每天的自主学习时间是 小时.
19.(2015春 大冶市期末)空气中由多种气体混合而成,为了简明扼要地介绍空气的组成情况,较好地描述空气中各种成分所占的百分比,最适合采用的统计图是 统计图.
20.(2015春 沭阳县期中)某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.
三.解答题(共5小题)
21.(2015 绵阳模拟)某中学在“五月份学习竞赛月”中举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 90 60 15
比例(%) 12 25 20 8 5
认真阅读统计图表后,回答下列问题:
(1)请补充完成统计表;
(2)本次参加比赛的总人数是 人,本次比赛项目的众数是 .
(3)根据上述数据,你可以获得什么信息.
22.(2015 酒泉)某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
进球数(个) 8 7 6 5 4 3
人数 2 1 4 7 8 2
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;
(2)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
23.(2015 自贡)在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
24.(2015 遂宁)交通指数是交通拥堵指数的简称,是综合反映道路畅通或拥堵的概念.其指数在100以内为畅通,200以上为严重拥堵,从某市交通指挥中心选取了5月1日至14日的交通状况,依据交通指数数据绘制的折线统计图如图所示,某人随机选取了5月1日至14日的某一天到达该市.
(1)请结合折线图分别找出交通为畅通和严重拥堵的天数;
(2)求此人到达当天的交通为严重拥堵的概率;
(3)由图判断从哪天开始连续三天的交通指数方差最大?(直接判断,不要求计算)
25.(2015 大连)某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 测试成绩(分) 人数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有 人,达到优秀的人数占本次测试总人数的百分比为 %.
(2)本次测试的学生数为 人,其中,体质健康成绩为及格的有 人,不及格的人数占本次测试总人数的百分比为 %.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
鲁教版六年级数学下册第8章8.4统计图的选择同步训练题参考答案
一.选择题(共10小题)
1.C 2.C 3.A 4.C 5.D6.D 7.C 8.C 9.D 10.B
二.填空题(共10小题)
11.9 8:00 0:00 12.37.5% 22.5% 40% 13.60 14.40% 15.40%
16.8 4 28 17.13 11 18.3 1.5 19.扇形 20.折线
三.解答题(共5小题)
21.解:(1)参赛的总人数是:60÷20%=300(人),
则参加书法的人数是:300×25%=75(人),
参加作文比赛的比例是:×100%=30%,
参加小品比赛的人数是:300×8%=24(人);
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 75 90 60 24 15
比例(%) 12 25 30 20 8 5
(2)参赛的总人数是300,本次比赛项目的众数是作文.
故答案是:300,作文;
(3)可以获得什么信息是:学生比较喜欢作文和书法.
22.解:(1)参加篮球训练的人数是:2+1+4+7+8+2=24(人).
训练后篮球定时定点投篮人均进球数==5(个).
故答案是:5;
(2)由扇形图可以看出:选择长跑训练的人数占全班人数的百分比=1﹣60%﹣10%﹣20%=10%,
则全班同学的人数为24÷60%=40(人),
故答案是:10%,40;
(3)设参加训练之前的人均进球数为x个,
则x(1+25%)=5,解得 x=4.
即参加训练之前的人均进球数是4个.
23.解:(1)(1﹣45%﹣5%﹣40%)×360°=36°;
(2)380×45%﹣67﹣44=60;
60﹣18﹣13﹣12﹣3=14;
(3)依题意,得45%×60=27,
答:唐老师应安排27课时复习“数与代数”内容.
故答案为:36,60,14.
24.解:(1)由纵坐标看出畅通的天数为7天,严重拥堵的天数为2天;
(2)此人到达当天的交通为严重拥堵的概率p==;
(3)由方差越大,数据波动越大,得
5、6、7三天数据波动大.
25.解:(1)本次测试学生体质健康成绩为良好的有36人.
达到优秀的人数占本次测试总人数的百分比为70%.
故答案是:36,70;
(2)调查的总人数是:140÷70%=200(人),
体质健康成绩为及格的有200﹣140﹣36﹣6=18(人),
不及格的人数占本次测试总人数的百分比是:×100%=3%.
故答案是:200,18,3%;
(3)本次测试学生体质健康成绩为良好的有36人,=18%,
估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数是:1800×(70%+18%)=1584(人).
一.选择题(共11小题)
1.(2013秋 太康县期末)下列图形中,多边形有( )
A.1个 B. 2个 C. 3个 D. 4个
2.(2015春 东平县校级月考)七边形的对角线共有( )
A.10条 B. 15条 C. 21条 D. 14条
3.(2015春 张家港市期末)从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是( )
A.6 B. 7 C. 8 D. 9
4.(2014秋 朝阳区期末)在六边形内任取一点,把这个点与六边形的各顶点分别连接可以得到( )
A.4个三角形 B. 5个三角形 C. 6个三角形 D. 7个三角形
5.(2015春 郑州期末)过多边形某个顶点的所有对角线,将这个多边形分成7个三角形,这个多边形是( )
A.八边形 B. 九边形 C. 十边形 D. 十一边形
6.(2015 重庆校级模拟)如图,正四边形有2条对角线,正五边形有5条对角线,正六边形有9条对角线,则正十边形有( )条对角线.
A.27 B. 35 C. 40 D. 44
7.(2015 无锡)八边形的内角和为( )
A.180° B. 360° C. 1080° D. 1440°
8.(2015 孝感)已知一个正多边形的每个外角等于60°,则这个正多边形是( )
A.正五边形 B. 正六边形 C. 正七边形 D. 正八边形
9.(2015 大庆)正n边形每个内角的大小都为108°,则n=( )
A.5 B. 6 C. 7 D. 8
10.(2015 宿迁)已知一个多边形的内角和等于它的外角和,则这个多边形的边数为( )
A.3 B. 4 C. 5 D. 6
11.(2015 莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
A.27 B. 35 C. 44 D. 54
二.填空题(共8小题)
12.(2014秋 吉州区期末)十边形有 个顶点,从一个顶点出发可画 条对角线,它共有 条对角线.
13.(2015春 海淀区校级期末)若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是 边形.
14.(2014秋 郸城县校级月考)一个四边形截去一个角后变成 .
15.(2015 辽阳)一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.(2015 北京)如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= .
(16题图) (17题图) (19题图)
17.(2015 盘锦二模)如图所示,一个角60°的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2= .
18.(2015 徐州)若正多边形的一个内角等于140°,则这个正多边形的边数是 .
19.(2015 巴彦淖尔)如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了 米.
三.解答题(共6小题)
20.(2015春 胶州市期末)如果一个多边形的各边都相邻,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° …
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
21.(2015春 长春期末)在一个正多边形中,一个内角是它相邻的一个外角的3倍.
(1)求这个多边形的每一个外角的度数.
(2)求这个多边形的边数.
22.(2015春 定陶县期末)观察下面图形,解答下列问题:
(1)观察规律,把下表填写完整:
边数 三 四 五 六 七 … n
对角线条数 0 2 5 …
(2)若一个多边形的内角和为1440°,求这个多边形的边数和对角线的条数.
23.(2015春 无锡期中)如图,
(1)在图1中,猜想:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2= 度.并试说明你猜想的理由.
(2)如果把图1称为2环三角形,它的内角和为:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2称为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1++∠A2+∠B2+∠C2+∠D2+∠E2
请你猜一猜,2环n边形的内角和为 度(只要求直接写出结论).
24.(2015春 盐都区期中)(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于
A.90° B.135° C.270° D.315°
(2)如图2,已知△ABC中,∠A=50°,剪去∠A后成四边形,则∠1+∠2= °.
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是 .
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
25.(2014秋 阜新月考)已知任意三角形的内角和为180°,试利用多边形中过某一顶点的对角线的条数,探求多边形内角和公式.
(1)如图所示,一个四边形可以分成 个三角形;于是四边形的内角和为 ;
(2)一个五边形可以分成 个三角形;于是五边形的内角和为 ;
(3)按此规律,n(n≥3)边形可分成多少个三角形?n边形的内角和是多少度?
青岛版七年级数学下册第13章13.2多边形同步训练题参考答案
一.选择题(共11小题)
1.B 2.D 3.C 4.C 5.B 6.B 7.C 8.B
9.A 10.B 11.C
二.填空题(共8小题)
12.10 7 35 13.13 14.三角形或四边形或五边形 15.6
16.360° 17.240° 18.9 19.120
三.解答题(共6小题)
20.解:(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° 36° 30° … ()°
(3)不存在,理由如下:
设存在正n边形使得∠α=21°,
得∠α=21°=()°.
解得:n=8,n是正整数,n=8(不符合题意要舍去),
不存在正n边形使得∠α=21°.
21.解:(1)设这个多边形的每一个外角的度数为x度.根据题意,得:
3x+x=180,
解得x=45.
故这个多边形的每一个外角的度数为45°;
(2)360°÷45°=8.
故这个多边形的边数为8.
22.解:(1)
边数 三 四 五 六 七 … n
对角线条数 0 2 5 9 14 …
(2)设多边形的边数为n.
则(n﹣2)×180=1440,解得n=10.
∴对角线的条数为:=35(条).
故答案为9,14,.
23.解:(1)连结B1B2,
则∠A2+∠C1=∠B1B2A2+∠B2B1C1,
∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=∠A1+∠B1+∠B1B2A2+∠B2B1C1+∠B2+∠C2=360度;
(2)如图,A1A2之间添加两条边,
可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2则∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2=∠A1+∠B1+∠C1+∠D1+∠A2+∠EA1D+∠A1EA2+∠EA2B2=720°;
2环n边形添加(n﹣2)条边,2环n边形的内角和成为(2n﹣2)边形的内角和.其内角和为180(2n﹣4)=360(n﹣2)度.
故答案为:(1)360;(2)360(n﹣2)
24.解:(1)∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2等于270°.
故选C;
(2)∠1+∠2=180°+50°=230°.
故答案是:230;
(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;
故答案是:∠1+∠2=180°+∠A;
(4)∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF
∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF
∴∠1+∠2=360°﹣2(∠AFE+∠AEF)
又∵∠AFE+∠AEF=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A,
即∠1+∠2=2∠A.
25.解:(1)∵四边形可分为两个三角形,
∴四边形的内角和=180°×2=360°.
故答案为:2,360°;
(2))∵五边形可分为三个三角形,
∴四边形的内角和=180°×3=540°.
故答案为:3,540°;
(3)由(1)、(2)可知,过n边形一个顶点的对角线将n边形可以分成(n﹣2)个三角形,于是n边形的内角和为(n﹣2) 180°.
故答案为:n﹣2,(n﹣2) 180°.
鲁教版六年级数学下册第8章8.4统计图的选择同步训练题(含答案)
一.选择题(共10小题)
1.(2015 贵阳模拟)小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
A. 阅读数量的平均数是57 B. 阅读数量的众数是42
C. 阅读数量的中位数是58 D. 有4个月的阅读数量超过60本
(1题图) (5题图)
2.(2015 杭州)如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中PM2.5浓度的中位数是112ug/m3;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是( )
A.①②③ B. ①②④ C. ①③④ D. ②③④
3.(2015 福州)下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B. 条形图 C. 折线图 D. 直方图
4.(2015春 嘉兴期末)要反映嘉兴市一天内气温的变化情况宜采用( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.频数分布直方图
5.(2015 杭州模拟)如图,是杭州PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
A.表示汽车尾气排放的圆心角约72° B.表示建筑扬尘的占6%
C.煤炭以及其他燃料燃放约为建筑扬尘的5倍 D.汽车尾气排放影响最大
6.(2014秋 东平县期末)李老师对本班50名学生的血型作了统计,列出如下的统计表,则本班AB型血的人数是( )
组别 A型 B型 AB型 O型
占全班人数的百分比 40% 30% 20% 10%
A.20人 B. 15人 C. 5人 D. 10人
7.(2015 扬州)如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )
A.音乐组 B. 美术组 C. 体育组 D. 科技组
(7题图) (8题图) (10题图)
8.(2015 邵阳)如图是某校参加各兴趣小组的学生人数分布扇形统计图,则参加人数最多的兴趣小组是( )
A.棋类 B. 书画 C. 球类 D. 演艺
9.(2015 恩施州)某中学开展“阳光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
A.240 B. 120 C. 80 D. 40
10.(2015 路北区一模)如图所示是甲、乙两户居民家庭全年各项支出的统计图.根据统计图,下列对两户居民家庭教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大 B.乙户比甲户大
C.甲、乙两户一样大 D.无法确定哪一户大
二.填空题(共10小题)
11.(2015春 南昌期末)下表是我市某一天在不同时段测得的气温情况:则这一天的气温的温差是 ℃,温度最接近的两个时间是 与 .
0:00 4:00 8:00 12:00 16:00 20:00
25℃ 27℃ 29℃ 32℃ 34℃ 30℃
12.(2014秋 围场县校级期末)已知全班有40位学生,他们有的步行,有的骑车,还有的乘车来上学,根据以下已知信息完成统计表:
上学方式 步行 骑车 乘车
划计 正正正
次数 9
占百分比
13.(2015 苏州)某学校“你最喜爱的球类运动”调查中,随机调查了若干名学生(每个学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人,则该校被调查的学生总人数为 名.
(13题图) (14题图) (15题图)
14.(2015 玉林)某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是 .
15.(2015 黄浦区二模)某校八年级共四个班,各班寒假外出旅游的学生人数如图所示,那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为 .
16.(2015春 和平区期末)七年级(1)班在一次数学抽测中某道选择题的答题情况如图(1),(2)所示.根据统计图可得选A的有 人,选B的有 人,选C的有 人.
(16题图) (17题图)
17.(2015 通州区一模)生物学研究表明在8﹣17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是 岁,在 岁时男生女生的身高增长速度是一样的.
18.(2015春 南昌期末)如图是小浩同学8月1日 7日毎天的自主学习时间统计图,则小浩同学一天中自主学习时间最长是 小时,这七天平均每天的自主学习时间是 小时.
19.(2015春 大冶市期末)空气中由多种气体混合而成,为了简明扼要地介绍空气的组成情况,较好地描述空气中各种成分所占的百分比,最适合采用的统计图是 统计图.
20.(2015春 沭阳县期中)某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.
三.解答题(共5小题)
21.(2015 绵阳模拟)某中学在“五月份学习竞赛月”中举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 90 60 15
比例(%) 12 25 20 8 5
认真阅读统计图表后,回答下列问题:
(1)请补充完成统计表;
(2)本次参加比赛的总人数是 人,本次比赛项目的众数是 .
(3)根据上述数据,你可以获得什么信息.
22.(2015 酒泉)某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
进球数(个) 8 7 6 5 4 3
人数 2 1 4 7 8 2
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;
(2)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
23.(2015 自贡)在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
24.(2015 遂宁)交通指数是交通拥堵指数的简称,是综合反映道路畅通或拥堵的概念.其指数在100以内为畅通,200以上为严重拥堵,从某市交通指挥中心选取了5月1日至14日的交通状况,依据交通指数数据绘制的折线统计图如图所示,某人随机选取了5月1日至14日的某一天到达该市.
(1)请结合折线图分别找出交通为畅通和严重拥堵的天数;
(2)求此人到达当天的交通为严重拥堵的概率;
(3)由图判断从哪天开始连续三天的交通指数方差最大?(直接判断,不要求计算)
25.(2015 大连)某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 测试成绩(分) 人数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有 人,达到优秀的人数占本次测试总人数的百分比为 %.
(2)本次测试的学生数为 人,其中,体质健康成绩为及格的有 人,不及格的人数占本次测试总人数的百分比为 %.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
鲁教版六年级数学下册第8章8.4统计图的选择同步训练题参考答案
一.选择题(共10小题)
1.C 2.C 3.A 4.C 5.D6.D 7.C 8.C 9.D 10.B
二.填空题(共10小题)
11.9 8:00 0:00 12.37.5% 22.5% 40% 13.60 14.40% 15.40%
16.8 4 28 17.13 11 18.3 1.5 19.扇形 20.折线
三.解答题(共5小题)
21.解:(1)参赛的总人数是:60÷20%=300(人),
则参加书法的人数是:300×25%=75(人),
参加作文比赛的比例是:×100%=30%,
参加小品比赛的人数是:300×8%=24(人);
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 75 90 60 24 15
比例(%) 12 25 30 20 8 5
(2)参赛的总人数是300,本次比赛项目的众数是作文.
故答案是:300,作文;
(3)可以获得什么信息是:学生比较喜欢作文和书法.
22.解:(1)参加篮球训练的人数是:2+1+4+7+8+2=24(人).
训练后篮球定时定点投篮人均进球数==5(个).
故答案是:5;
(2)由扇形图可以看出:选择长跑训练的人数占全班人数的百分比=1﹣60%﹣10%﹣20%=10%,
则全班同学的人数为24÷60%=40(人),
故答案是:10%,40;
(3)设参加训练之前的人均进球数为x个,
则x(1+25%)=5,解得 x=4.
即参加训练之前的人均进球数是4个.
23.解:(1)(1﹣45%﹣5%﹣40%)×360°=36°;
(2)380×45%﹣67﹣44=60;
60﹣18﹣13﹣12﹣3=14;
(3)依题意,得45%×60=27,
答:唐老师应安排27课时复习“数与代数”内容.
故答案为:36,60,14.
24.解:(1)由纵坐标看出畅通的天数为7天,严重拥堵的天数为2天;
(2)此人到达当天的交通为严重拥堵的概率p==;
(3)由方差越大,数据波动越大,得
5、6、7三天数据波动大.
25.解:(1)本次测试学生体质健康成绩为良好的有36人.
达到优秀的人数占本次测试总人数的百分比为70%.
故答案是:36,70;
(2)调查的总人数是:140÷70%=200(人),
体质健康成绩为及格的有200﹣140﹣36﹣6=18(人),
不及格的人数占本次测试总人数的百分比是:×100%=3%.
故答案是:200,18,3%;
(3)本次测试学生体质健康成绩为良好的有36人,=18%,
估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数是:1800×(70%+18%)=1584(人).
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
