人教版七下数学第七章 平面直角坐标系单元测试卷(含答案)
文档属性
| 名称 | 人教版七下数学第七章 平面直角坐标系单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 531.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 09:02:23 | ||
图片预览




文档简介
第七单元测试卷
一、选择题(共14题.1~10题每题3分,11~14题每题2分,共38分)
1.2023年5月30日神舟十六号飞船在甘肃酒泉卫星中心发射升空,驻留约5个月,计划11月返回地球东风着陆场,下列描述能确定飞船着陆位置的是 ( )
A.内蒙古自治区
B.酒泉卫星发射中心东北方向800 km处
C.东经130°25'~98°10'
D.北纬54°35'~38°20'
2.在平面直角坐标系中,点M(m-1,2m)在x轴上,则点M的坐标是
( )
A.(1,0) B.(-1,0) C.(0,2) D.(0,-1)
3.在平面直角坐标系中,点P(3,-7)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.如果第二列第一行用有序数对(2,1)表示,那么数对(3,6)和(3,4)表示的位置是 ( )
A.同一行 B.同一列
C.同行同列 D.不同行不同列
5.经过A(2,3),B(-4,3)两点作直线AB,则直线AB ( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.无法确定
6.已知A(a,0)和B(0,10)两点,且AB与坐标轴围成的三角形的面积等于20,则a的值为 ( )
A.2 B.4
C.0或4 D.4或-4
7.如图,在一次活动中,位于A处的1班准备前往相距5 km的B处与2班会合,用方向和距离描述2班相对于1班的位置 ( )
A.2班在1班南偏西50°处
B.2班在1班南偏西50°方向上5 km处
C.1班在2班5 km处
D.1班在2班北偏东50°方向上5 km处
8.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),
B(1,2),平移线段AB,得到线段A'B',已知A'的坐标为(3,-1),则点B'的坐标为 ( )
A.(4,2) B.(5,2)
C.(6,2) D.(5,3)
9.在下列四点中,与点(-3,4)所连得到的直线不与y轴相交的是 ( )
A.(-2,3) B.(2,-3)
C.(3,2) D.(-3,2)
10.已知点A(1,2a+1),B(-a,a-3),若线段AB∥x轴,则三角形AOB的面积
为 ( )
A.21 B.28 C.14 D.10.5
11.海平面上,有一个灯塔,测得海岛A在灯塔北偏东30°方向上,同时测得海岛B在灯塔北偏东60°的方向上,则灯塔的位置可以是 ( )
A.点O1 B.点O2 C.点O3 D.点O4
12.若点M(2-a,3a+6)到两坐标轴的距离相等,则点M的坐标( )
A.(6,-6) B.(3,3)
C.(-6,6)或(-3,3) D.(6,-6)或(3,3)
13.在平面直角坐标系中,将点B(-2,-4)向上平移6个单位长度后得到点A.若点C位于第三象限,且为线段AB的三等分点,点P(m,2m)在第一象限,三角形APC的面积为6,则点P的坐标为 ( )
A.(3,6) B.(2,4) C.(4,8) D.(1,2)
14.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到点P3(3,-2),第四次运动到点P4(4,0),第五次运动到点P5(5,2),第六次运动到点P6(6,0)……按这样的运动规律,点P2 024的纵坐标是( )
A.-2 B.0 C.1 D.2
二、填空题(共3题,15~16题每空2分,17题3分,共11分)
15.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是_________;若点P(沿水平或竖直方向)两次平移后与原点重合,则点P的平移方式可能是____________________________________。
16.有甲、乙、丙三人,它们所在的位置不同,他们三人都以相同的单位长度建立不同的坐标系,甲说:“如果以我为坐标原点,乙的位置是(4,3)”;丙说:“我先向左平移3个单位长度,再向下平移4个单位长度就到了乙的位置”;如果以乙为坐标原点,甲和丙的位置分别是__________,__________.
17.如图是莫高窟景区游览路线图的一部分,在图中建立平面直角坐标系,若表示敦煌研究院院史陈列馆的点的坐标为(-3,0),表示九层楼的点的坐标为(0,1),则表示美术馆的点的坐标为__________.
三、解答题(共51分)
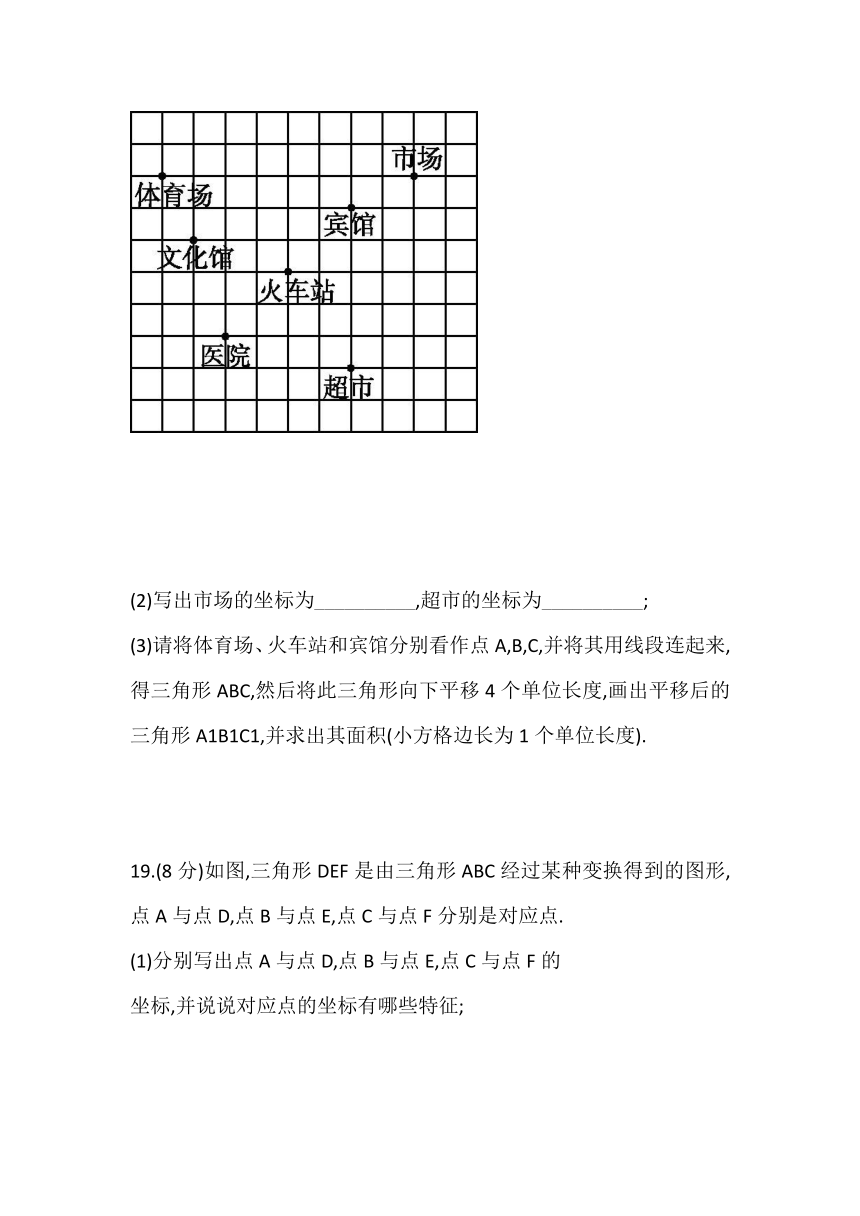
18.(8分)如图,这是某市部分简图.
(1)请你以火车站为原点建立平面直角坐标系;
(2)写出市场的坐标为__________,超市的坐标为__________;
(3)请将体育场、火车站和宾馆分别看作点A,B,C,并将其用线段连起来,得三角形ABC,然后将此三角形向下平移4个单位长度,画出平移后的三角形A1B1C1,并求出其面积(小方格边长为1个单位长度).
19.(8分)如图,三角形DEF是由三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点.
(1)分别写出点A与点D,点B与点E,点C与点F的
坐标,并说说对应点的坐标有哪些特征;
20.(8分)在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a阶派生点”(其中a为常数,且a≠0).例如:点P(1,4)的“2阶派生点”为点Q(2×1+4,1+2×4),即点Q的坐标为(6,9).
(1)若点P的坐标为(-1,5),求它的“3阶派生点”的坐标;
(2)若点P(c+1,2c-1)先向左平移2个单位长度,再向上平移1个单位长度后得到了点P1,点P1的“-3阶派生点”P2位于坐标轴上,求点P2的坐标.
21.(8分)(1)已知点P(2x+3,4x-7)的横坐标减纵坐标的差为6,求这个点到x轴、y轴的距离;
(2)已知点A(2x-3,6-x)到两个坐标轴的距离相等,且在第二象限,求点A的坐标;
(3)已知线段AB平行于y轴,点A的坐标为(-2,3),且AB=4,求点B的坐标.
(2)求三角形ACD的面积;
(3)若P为x轴上的一个动点,是否存在点P,使三角形PAO的面积等于三角形PAC面积的2倍,若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.(10分)如图,在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t秒.
(1)直接写出点B和点C的坐标.
(2)当点P运动时,用含t的式子表示线段AP的长;
参考答案
1、B
2、B
3、D
4、B
5、A
6、D
7.B
8、B
9.D
10.D
11.A
12.D
13.D
14.B
15.(-3,5) 先向右平移3个单位长度,再向下平移5个单位长度(或先向下平移5个单位长度,再向右平移3个单位长度)
16.(-4,-3) (3,4)
17.(5,-1)
18.(1)
(2)(4,3) (2,-3)
(3)
19.(1)解:由图,得A(2,3),D(-2,-3);B(1,2),E(-1,-2);
C(3,1),F(-3,-1).
由对应点的坐标,可得对应点的横坐标与纵坐标都互为相反数.
(2)
20.(1)
解:根据新定义,得点P的“3阶派生点”的横坐标为3×(-1)+5=2,纵坐标为-1+3×5=14,
∴点P的“3阶派生点”的坐标为(2,14)
(2)
21(1)
解:根据题意,得(2x+3)-(4x-7)=6,
解得x=2,∴P(7,1).
∴这个点到x轴的距离是1,到y轴的距离是7
(2)解:∵A(2x-3,6-x)在第二象限,
∴2x-3<0,6-x>0.
根据题意,得-(2x-3)=6-x,解得x=-3,
∴A(-9,9)
(3)解:∵线段AB平行于y轴,点A的坐标为(-2,3),
∴点B的横坐标是-2,
又∵AB=4,
∴当B点在A点上方时,点B的纵坐标是3+4=7;
当B点在A点下方时,点B的纵坐标是3-4=-1.
∴点B坐标是(-2,7)或(-2,-1)
22.(1)(0,4) (-2,0) (4,0)
(2)
(3)
23(1)解:(1)B(0,6),C(8,0)
(2)
解:由A(8,6),B(0,6),C(8,0),得AB=8,AC=6,8÷2=4(秒),(8+6)÷2=7(秒).
当点P在线段BA上时,
则AP=AB-BP,BP=2t,∴AP=8-2t(0≤t<4);
当点P在线段AC上时,
∴AP=2t-AB=2t-8(4≤t≤7).
(3)
一、选择题(共14题.1~10题每题3分,11~14题每题2分,共38分)
1.2023年5月30日神舟十六号飞船在甘肃酒泉卫星中心发射升空,驻留约5个月,计划11月返回地球东风着陆场,下列描述能确定飞船着陆位置的是 ( )
A.内蒙古自治区
B.酒泉卫星发射中心东北方向800 km处
C.东经130°25'~98°10'
D.北纬54°35'~38°20'
2.在平面直角坐标系中,点M(m-1,2m)在x轴上,则点M的坐标是
( )
A.(1,0) B.(-1,0) C.(0,2) D.(0,-1)
3.在平面直角坐标系中,点P(3,-7)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.如果第二列第一行用有序数对(2,1)表示,那么数对(3,6)和(3,4)表示的位置是 ( )
A.同一行 B.同一列
C.同行同列 D.不同行不同列
5.经过A(2,3),B(-4,3)两点作直线AB,则直线AB ( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.无法确定
6.已知A(a,0)和B(0,10)两点,且AB与坐标轴围成的三角形的面积等于20,则a的值为 ( )
A.2 B.4
C.0或4 D.4或-4
7.如图,在一次活动中,位于A处的1班准备前往相距5 km的B处与2班会合,用方向和距离描述2班相对于1班的位置 ( )
A.2班在1班南偏西50°处
B.2班在1班南偏西50°方向上5 km处
C.1班在2班5 km处
D.1班在2班北偏东50°方向上5 km处
8.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),
B(1,2),平移线段AB,得到线段A'B',已知A'的坐标为(3,-1),则点B'的坐标为 ( )
A.(4,2) B.(5,2)
C.(6,2) D.(5,3)
9.在下列四点中,与点(-3,4)所连得到的直线不与y轴相交的是 ( )
A.(-2,3) B.(2,-3)
C.(3,2) D.(-3,2)
10.已知点A(1,2a+1),B(-a,a-3),若线段AB∥x轴,则三角形AOB的面积
为 ( )
A.21 B.28 C.14 D.10.5
11.海平面上,有一个灯塔,测得海岛A在灯塔北偏东30°方向上,同时测得海岛B在灯塔北偏东60°的方向上,则灯塔的位置可以是 ( )
A.点O1 B.点O2 C.点O3 D.点O4
12.若点M(2-a,3a+6)到两坐标轴的距离相等,则点M的坐标( )
A.(6,-6) B.(3,3)
C.(-6,6)或(-3,3) D.(6,-6)或(3,3)
13.在平面直角坐标系中,将点B(-2,-4)向上平移6个单位长度后得到点A.若点C位于第三象限,且为线段AB的三等分点,点P(m,2m)在第一象限,三角形APC的面积为6,则点P的坐标为 ( )
A.(3,6) B.(2,4) C.(4,8) D.(1,2)
14.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到点P3(3,-2),第四次运动到点P4(4,0),第五次运动到点P5(5,2),第六次运动到点P6(6,0)……按这样的运动规律,点P2 024的纵坐标是( )
A.-2 B.0 C.1 D.2
二、填空题(共3题,15~16题每空2分,17题3分,共11分)
15.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是_________;若点P(沿水平或竖直方向)两次平移后与原点重合,则点P的平移方式可能是____________________________________。
16.有甲、乙、丙三人,它们所在的位置不同,他们三人都以相同的单位长度建立不同的坐标系,甲说:“如果以我为坐标原点,乙的位置是(4,3)”;丙说:“我先向左平移3个单位长度,再向下平移4个单位长度就到了乙的位置”;如果以乙为坐标原点,甲和丙的位置分别是__________,__________.
17.如图是莫高窟景区游览路线图的一部分,在图中建立平面直角坐标系,若表示敦煌研究院院史陈列馆的点的坐标为(-3,0),表示九层楼的点的坐标为(0,1),则表示美术馆的点的坐标为__________.
三、解答题(共51分)
18.(8分)如图,这是某市部分简图.
(1)请你以火车站为原点建立平面直角坐标系;
(2)写出市场的坐标为__________,超市的坐标为__________;
(3)请将体育场、火车站和宾馆分别看作点A,B,C,并将其用线段连起来,得三角形ABC,然后将此三角形向下平移4个单位长度,画出平移后的三角形A1B1C1,并求出其面积(小方格边长为1个单位长度).
19.(8分)如图,三角形DEF是由三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点.
(1)分别写出点A与点D,点B与点E,点C与点F的
坐标,并说说对应点的坐标有哪些特征;
20.(8分)在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a阶派生点”(其中a为常数,且a≠0).例如:点P(1,4)的“2阶派生点”为点Q(2×1+4,1+2×4),即点Q的坐标为(6,9).
(1)若点P的坐标为(-1,5),求它的“3阶派生点”的坐标;
(2)若点P(c+1,2c-1)先向左平移2个单位长度,再向上平移1个单位长度后得到了点P1,点P1的“-3阶派生点”P2位于坐标轴上,求点P2的坐标.
21.(8分)(1)已知点P(2x+3,4x-7)的横坐标减纵坐标的差为6,求这个点到x轴、y轴的距离;
(2)已知点A(2x-3,6-x)到两个坐标轴的距离相等,且在第二象限,求点A的坐标;
(3)已知线段AB平行于y轴,点A的坐标为(-2,3),且AB=4,求点B的坐标.
(2)求三角形ACD的面积;
(3)若P为x轴上的一个动点,是否存在点P,使三角形PAO的面积等于三角形PAC面积的2倍,若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.(10分)如图,在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t秒.
(1)直接写出点B和点C的坐标.
(2)当点P运动时,用含t的式子表示线段AP的长;
参考答案
1、B
2、B
3、D
4、B
5、A
6、D
7.B
8、B
9.D
10.D
11.A
12.D
13.D
14.B
15.(-3,5) 先向右平移3个单位长度,再向下平移5个单位长度(或先向下平移5个单位长度,再向右平移3个单位长度)
16.(-4,-3) (3,4)
17.(5,-1)
18.(1)
(2)(4,3) (2,-3)
(3)
19.(1)解:由图,得A(2,3),D(-2,-3);B(1,2),E(-1,-2);
C(3,1),F(-3,-1).
由对应点的坐标,可得对应点的横坐标与纵坐标都互为相反数.
(2)
20.(1)
解:根据新定义,得点P的“3阶派生点”的横坐标为3×(-1)+5=2,纵坐标为-1+3×5=14,
∴点P的“3阶派生点”的坐标为(2,14)
(2)
21(1)
解:根据题意,得(2x+3)-(4x-7)=6,
解得x=2,∴P(7,1).
∴这个点到x轴的距离是1,到y轴的距离是7
(2)解:∵A(2x-3,6-x)在第二象限,
∴2x-3<0,6-x>0.
根据题意,得-(2x-3)=6-x,解得x=-3,
∴A(-9,9)
(3)解:∵线段AB平行于y轴,点A的坐标为(-2,3),
∴点B的横坐标是-2,
又∵AB=4,
∴当B点在A点上方时,点B的纵坐标是3+4=7;
当B点在A点下方时,点B的纵坐标是3-4=-1.
∴点B坐标是(-2,7)或(-2,-1)
22.(1)(0,4) (-2,0) (4,0)
(2)
(3)
23(1)解:(1)B(0,6),C(8,0)
(2)
解:由A(8,6),B(0,6),C(8,0),得AB=8,AC=6,8÷2=4(秒),(8+6)÷2=7(秒).
当点P在线段BA上时,
则AP=AB-BP,BP=2t,∴AP=8-2t(0≤t<4);
当点P在线段AC上时,
∴AP=2t-AB=2t-8(4≤t≤7).
(3)
