7.3.2多边形的内角和
图片预览





文档简介
课件23张PPT。7.3.2探索多边形的内角和学习目标1.通过测量、类比、推导等过程,探索多边形的内角和公式。
2.通过将多边形转化为三角形的探究过程,体会化未知为已知,从特殊到一般的解决问题方法。重点:探索多边形的内角和公式。
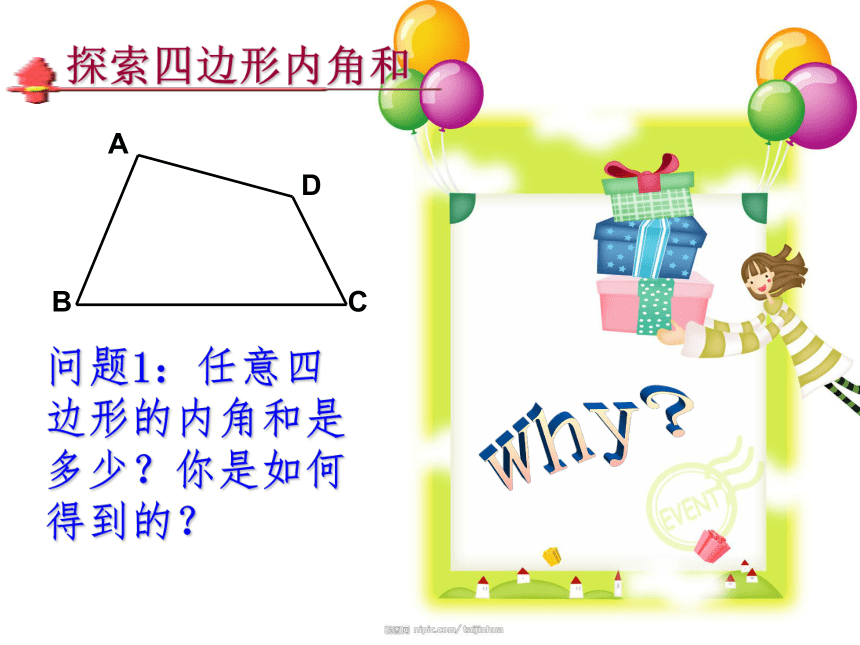
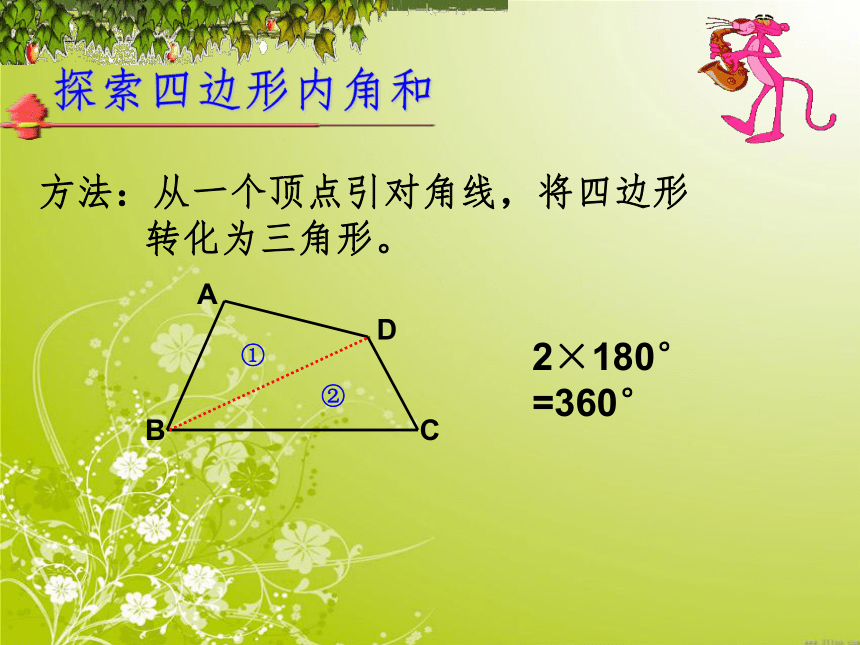
难点:探索多边形内角和公式时,如何将多边形转化为三角形。奥 运 畅 想小明想:2008年奥运会已经结束,如果设计一个内角和为20080的多边形图案多有纪念意义,你说小明的想法能实现吗?为什么?三角形内角和 是180°长方形的内角和是360°多边形的内角和开始探索啦!正方形的内角和是360°Why?问题1:任意四边形的内角和是多少?你是如何得到的?探索四边形内角和探索四边形内角和方法:从一个顶点引对角线,将四边形
转化为三角形。2×180°
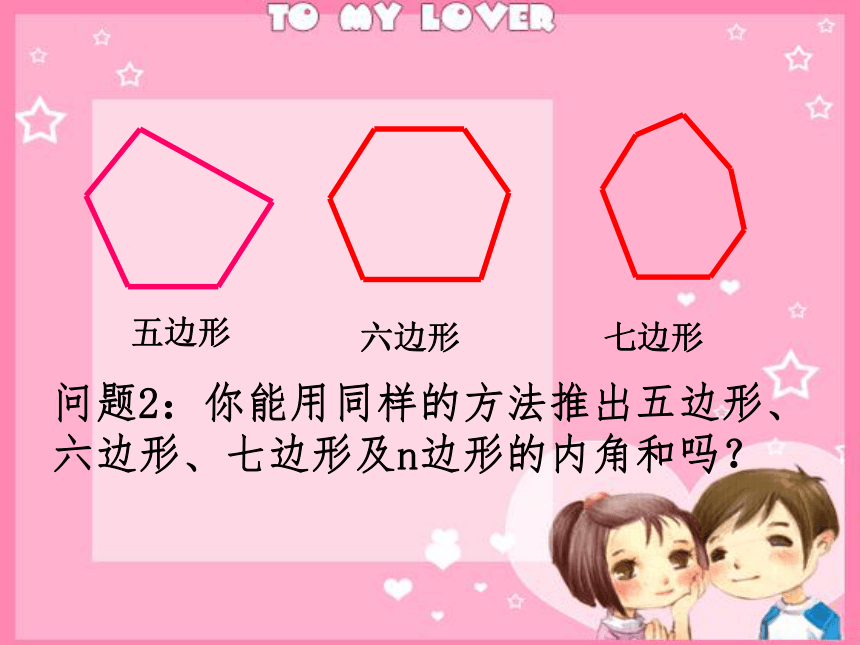
=360°①②问题2:你能用同样的方法推出五边形、六边形、七边形及n边形的内角和吗?五边形六边形七边形 探索五、六、七边形及n 边形的内角和 五边形六边形七边形三角形四边形1×180°=180° 2×180°=360° 3×180°=540° 4×180°=720° 5×180°=900° (n-2)·180?234n-3345n-2(1)n边形的内角和公式:
(n-2)·180?总 结(2)探索多边形内角和的方法:
利用辅助线将多边形转化为三角形。常见基础题型:已知多边形边数n ,
求多边形内角和;
已知多边形内角和,
求多边形边数。题型1:题型2:1、八边形的内角和等于 度;例题:解题方法归纳:
直接利用公式,将n代入公式(n-2)·180?中计算得出。10801800题型1:(8-2)×180°=1080°2、十二边形的内角和等于 度。(12-2)×180°=1800°基础训练540°900°720°1440°2700°1、五边形内角和为_______。
2、六边形内角和为_______。
3、七边形内角和为_______。
4、十边形的内角和为_______。
5、十七边形的内角和为_______。例题: 如果一个多边形的内角和为1080°,则它是 边形。题型2:解题方法归纳:
根据内角和公式和条件构建一元一次方程,解出边数n。由(n-2)·180?=1080°n=8八基础训练
6、多边形内角和为1800°,则它是_____边形。
7、多边形内角和为900°,则它是_____边形。
8、多边形内角和为3600°,则它是_______边形。
十二七二十二 9、下面是小明准备用来做徽章
的木板,求下列木板图中x的值.x=65°x=60°x=95°那么正五边形、正六边形、正八边形、正n边形的每个内角分别是多少度呢? ……
正n边形(5-2)×180°
5
=108°(6-2)×180°
6
=120°(8-2)×180°
8
=135°(n-2)×180°
nNow I can ……正n边形的每个内角为:2、若一个正多边形每个内角
为120度,则这个多边形是
边形。例题:正六1、正十边形的每个内角度数为 ___________。144°拓展训练
2、一个多边形每个内角为108°,则这个多边形为_____边形。
正五1、正十二边形的每个内角度数是__________。150°奥 运 畅 想小明想:2008年奥运会已经结束,如果设计一个内角和为20080的多边形图案多有纪念意义,你说小明的想法能实现吗?为什么?小结:这节课你学到了什么?有一张长方形的桌面,现在小明要想锯掉它的一个角,剩下残余桌面所有的内角和是多少?课后思考题:如图所示:四边形ABCD中,AB⊥AD,BC ⊥CD。
请问:∠B和∠D之间存在怎样的关系?
2.通过将多边形转化为三角形的探究过程,体会化未知为已知,从特殊到一般的解决问题方法。重点:探索多边形的内角和公式。
难点:探索多边形内角和公式时,如何将多边形转化为三角形。奥 运 畅 想小明想:2008年奥运会已经结束,如果设计一个内角和为20080的多边形图案多有纪念意义,你说小明的想法能实现吗?为什么?三角形内角和 是180°长方形的内角和是360°多边形的内角和开始探索啦!正方形的内角和是360°Why?问题1:任意四边形的内角和是多少?你是如何得到的?探索四边形内角和探索四边形内角和方法:从一个顶点引对角线,将四边形
转化为三角形。2×180°
=360°①②问题2:你能用同样的方法推出五边形、六边形、七边形及n边形的内角和吗?五边形六边形七边形 探索五、六、七边形及n 边形的内角和 五边形六边形七边形三角形四边形1×180°=180° 2×180°=360° 3×180°=540° 4×180°=720° 5×180°=900° (n-2)·180?234n-3345n-2(1)n边形的内角和公式:
(n-2)·180?总 结(2)探索多边形内角和的方法:
利用辅助线将多边形转化为三角形。常见基础题型:已知多边形边数n ,
求多边形内角和;
已知多边形内角和,
求多边形边数。题型1:题型2:1、八边形的内角和等于 度;例题:解题方法归纳:
直接利用公式,将n代入公式(n-2)·180?中计算得出。10801800题型1:(8-2)×180°=1080°2、十二边形的内角和等于 度。(12-2)×180°=1800°基础训练540°900°720°1440°2700°1、五边形内角和为_______。
2、六边形内角和为_______。
3、七边形内角和为_______。
4、十边形的内角和为_______。
5、十七边形的内角和为_______。例题: 如果一个多边形的内角和为1080°,则它是 边形。题型2:解题方法归纳:
根据内角和公式和条件构建一元一次方程,解出边数n。由(n-2)·180?=1080°n=8八基础训练
6、多边形内角和为1800°,则它是_____边形。
7、多边形内角和为900°,则它是_____边形。
8、多边形内角和为3600°,则它是_______边形。
十二七二十二 9、下面是小明准备用来做徽章
的木板,求下列木板图中x的值.x=65°x=60°x=95°那么正五边形、正六边形、正八边形、正n边形的每个内角分别是多少度呢? ……
正n边形(5-2)×180°
5
=108°(6-2)×180°
6
=120°(8-2)×180°
8
=135°(n-2)×180°
nNow I can ……正n边形的每个内角为:2、若一个正多边形每个内角
为120度,则这个多边形是
边形。例题:正六1、正十边形的每个内角度数为 ___________。144°拓展训练
2、一个多边形每个内角为108°,则这个多边形为_____边形。
正五1、正十二边形的每个内角度数是__________。150°奥 运 畅 想小明想:2008年奥运会已经结束,如果设计一个内角和为20080的多边形图案多有纪念意义,你说小明的想法能实现吗?为什么?小结:这节课你学到了什么?有一张长方形的桌面,现在小明要想锯掉它的一个角,剩下残余桌面所有的内角和是多少?课后思考题:如图所示:四边形ABCD中,AB⊥AD,BC ⊥CD。
请问:∠B和∠D之间存在怎样的关系?
