应用题专项突破 圆锥的体积(含答案)数学六年级下册北师大版
文档属性
| 名称 | 应用题专项突破 圆锥的体积(含答案)数学六年级下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 550.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 09:38:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
应用题专项突破:圆锥的体积-数学六年级下册北师大版
1.一个圆锥形麦堆高1.5米,底面半径是2米,如果每立方米小麦重235千克,这堆小麦重多少千克?
2.一个长方体玻璃容器从里面量,长10厘米,宽8厘米,高15厘米。里面盛有水,水中浸没着一个高为6厘米的圆锥形铅锤,把铅锤从水中取出后水面下降了0.5厘米,这个圆锥形铅锤的底面积是多少平方厘米?
3.一堆玉米堆成圆锥形,底面周长是18.84米,高是2米。
(1)如果把这些玉米装在内底面半径是2米的圆柱形粮仓里,能装多高?
(2)如果每立方米玉米重750千克,这些玉米有多少吨?
4.打谷场上有一堆圆锥形谷堆,测得谷堆的底面周长是62.8米,高是3米,要把这些稻谷分装在底面直径是2.4米,高2.5米的圆柱形粮仓里,需要多少个这样的粮仓?
5.在一个直径是2分米的圆柱形容器中,放入一个底面半径是3厘米的圆锥形铁块,全部浸没在水中,这时水面上升0.3厘米。圆锥形铁块的高是多少厘米?
6.一顶近似圆锥形的旅游帐篷,它的底面半径是4米,高是3米。
(1)按每人的活动面积为2平方米计算,每顶帐篷大约可以住几人?
(2)每顶帐篷内空间有多大?
7.有一个长方体的水槽,槽内有一个圆锥形的零件完全浸在水中,已知水槽的长为1米,宽为5分米,水面高0.5米,零件的底面直径为40厘米。当零件从水中取出后,水面下降了6.28厘米,求这个圆锥形零件的高是多少米?
8.建筑工地上有一个圆锥形的沙堆,底面积是25平方米,高是1.8米。用这堆沙在40米宽的银湖中路东段路上铺0.05米厚的路面,能铺多少米?
9.蒙古包也称“毡包”,是蒙古族传统民居。如图蒙古包是由一个圆柱体和一个圆锥体组成。
(1)这个蒙古包至少占地多大?
(2)这个蒙古包至少占了多大的空间?
10.有一块棱长6分米的正方体木料,把这块木料加工成一个最大的圆锥体。这个圆锥体的体积是多少?
11.一种深受小朋友们喜爱的玩具——陀螺(如下图)。陀螺上部分是圆柱,下部分是圆锥。圆柱的底面半径是3厘米,高4厘米;圆锥的高是圆柱高的。这个陀螺的体积是多少立方厘米?
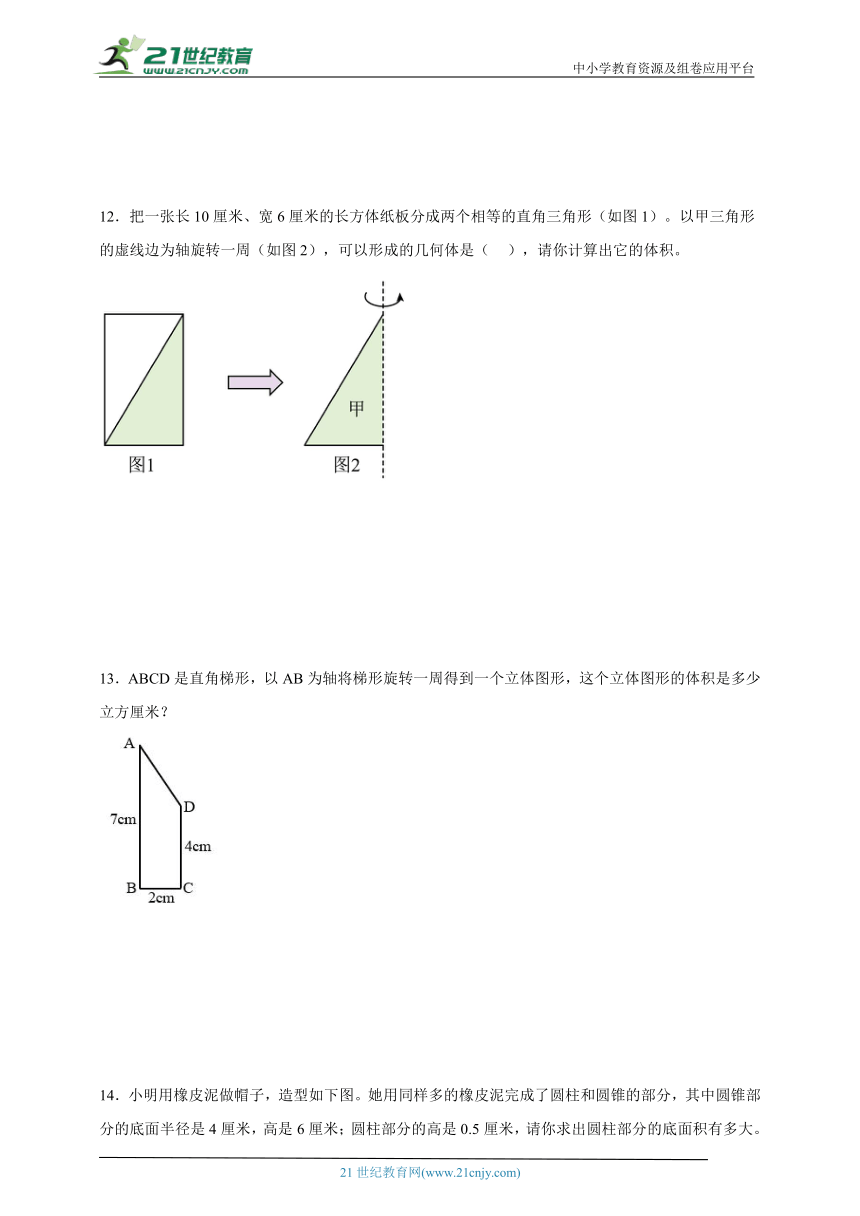
12.把一张长10厘米、宽6厘米的长方体纸板分成两个相等的直角三角形(如图1)。以甲三角形的虚线边为轴旋转一周(如图2),可以形成的几何体是( ),请你计算出它的体积。
13.ABCD是直角梯形,以AB为轴将梯形旋转一周得到一个立体图形,这个立体图形的体积是多少立方厘米?
14.小明用橡皮泥做帽子,造型如下图。她用同样多的橡皮泥完成了圆柱和圆锥的部分,其中圆锥部分的底面半径是4厘米,高是6厘米;圆柱部分的高是0.5厘米,请你求出圆柱部分的底面积有多大。
15.社区开展文明创建,加强绿地建设,准备建造一个地面直径是20米、高0.5米的圆柱形花坛(坛壁厚度忽略不计)。
(1)如果在花坛外侧面贴上瓷砖,贴瓷砖的面积是多少平方米?
(2)现有一堆泥土,近似于一个圆锥。经测量土堆的底面周长是31.4米,高是3米。请你算一算,这堆泥土能填满这个花坛吗?
16.如图,将等底等高的两个零件圆锥A和圆柱B重新熔化,铸造成一个新的零件长方体C,已知圆柱的底面半径3厘米,高是5厘米。长方体C的体积是多少立方厘米?
17.如图30-1,这是一个由等底等高的圆柱和圆锥组合而成的计时工具,圆锥内灌满了有颜色水。其中圆锥的高为6厘米,底面半径为3厘米。已知水的流速是1.57立方厘米/分钟。
(1)圆锥内漏完水需要多少时间?
(2)请你在图30-2中用阴影表示出此时圆柱内的水。
18.一个底面半径是12厘米,高是15厘米的圆锥形容器里装满水。如果将这些水倒入一个底面半径是8厘米,高是10厘米的圆柱形容器里,将有多少毫升的水倒不下?
19.建筑师傅要将一堆圆锥形的沙土运到冬奥会建筑工地。量得沙堆底面周长12.56米,高1.5米,如果用一辆一次能运1.3立方米的汽车运,那么要多少次才能运完?
20.一个密闭玻璃容器是由一个圆柱和一个圆锥组成的,里面装有一些水(如图1,单位:厘米,玻璃的厚度忽略不计)。
(1)容器中水的体积是多少立方厘米?
(2)如果将这个容器倒过来(如图2),从水面到圆锥顶点的高度是多少厘米?
21.2022年6月5日,搭载陈冬(涧西区人)为指令长的三位航天员的“神舟十四号”载人飞船长征二号F遥十四运载火箭在酒泉卫星发射中心点火发射,发射取得圆满成功。
(1)长征二号F遥十四运载火箭的总长58.34米,小明收藏了这一型号的火箭模型,模型的高度与实际高度的比是1∶50,这一模型的高度是多少厘米?
(2)整流罩是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。下图是某型号运载火箭整流罩的简约示意图,忽略整流罩本身的厚度不计,该整流罩的容积是多少?
22.把底面积相等的一块圆锥形铁块和一块圆柱形铁块先后浸没在长是20cm、宽是18cm的盛有水的长方体容器中,先放入圆锥形铁块,水面上升了0.5cm;再放入圆柱形铁块,水面上升了2cm,没有水溢出。
(1)如果圆锥形铁块的高是12cm,那么它的底面积是多少平方厘米?
(2)如果每立方厘米铁块重7.8g,那么这个圆柱形铁块重多少克?
参考答案:
1.1475.8千克
【分析】首先根据圆锥的体积公式:V=求出沙堆的体积,然后用沙堆的体积乘每立方米小麦的质量即可。
【详解】
=6.28×235
=1475.8(千克)
答:这堆小麦重1475.8千克。
【点睛】此题考查了圆锥体积的求解方法,要注意最后不要忘记乘。
2.20平方厘米
【分析】铅锤的体积等于容器中下降部分水的体积,根据“长方体的体积=长×宽×高”求出下降部分水的体积,再利用“”求出圆锥的底面积,据此解答。
【详解】铅锤的体积:10×8×0.5
=80×0.5
=40(立方厘米)
铅锤的底面积:40×3÷6
=120÷6
=20(平方厘米)
答:这个圆锥形铅锤的底面积是20平方厘米。
【点睛】理解容器中下降部分水的体积等于圆锥的体积是解答题目的关键。
3.(1)1.5米;
(2)14.13吨
【分析】(1)由题意可知,把玉米装在圆柱形的粮仓里玉米的体积不变,先求出圆锥的底面半径,再根据“”求出这堆玉米的体积,最后利用“”求出玉米装在圆柱形粮仓里面的高度;
(2)先利用“”求出这堆玉米的体积,再乘每立方米玉米的重量求出玉米的总重量,最后把单位转化为“吨”,据此解答。
【详解】(1)18.84÷3.14÷2
=6÷2
=3(米)
=
=
=
=1.5(米)
答:能装1.5米。
(2)
=
=
=
=4500×3.14
=14130(千克)
14130千克=14.13吨
答:这些玉米有14.13吨。
【点睛】本题主要考查圆锥和圆柱体积公式的应用,熟练掌握并灵活运用公式是解答题目的关键。
4.28个
【分析】先根据圆锥的底面周长求出圆锥的底面半径,再利用“”求出这堆稻谷的体积,并利用“”求出每个圆柱形粮仓可以装稻谷的体积,需要粮仓的数量=圆锥的体积÷圆柱的体积,余下的稻谷装不满一个粮仓时需要多准备一个粮仓,结果用进一法取整数,据此解答。
【详解】62.8÷3.14÷2
=20÷2
=10(米)
=
=
=(立方米)
=
=
=(立方米)
÷≈28(个)
答:需要28个这样的粮仓。
【点睛】熟练掌握圆柱和圆锥的体积计算公式,并找出合适的取近似值的方法是解答题目的关键。
5.10厘米
【分析】水面上升的体积就是圆锥形铁块体积,根据圆柱体积公式,用容器底面积×上升的水的高度,即可求出铁块体积,再根据圆锥的高=体积×3÷底面积,列式解答即可。
【详解】2分米=20厘米
3.14×(20÷2)2×0.3×3÷(3.14×32)
=3.14×100×0.3×3÷(3.14×9)
=314×0.3×3÷28.26
=94.2×3÷28.26
=282.6÷28.26
=10(厘米)
答:圆锥形铁块的高是10厘米。
【点睛】关键是掌握并灵活运用圆柱和圆锥的体积公式。
6.(1)25人;(2)50.24立方米
【分析】(1)根据圆的面积S=πr2,求出圆锥的底面积,再除以每个人的活动面积即可。
(2)根据圆锥的体积V=πr2h,代入数据计算即可。
【详解】(1)3.14×42÷2
=50.24÷2
≈25(人)
答:每顶帐篷大约可以住25人。
(2)×3.14×42×3
=3.14×16
=50.24(立方米)
答:每顶帐篷内空间有50.24立方米。
【点睛】此题考查了有关圆锥的实际应用,明确问题所求牢记圆锥体积公式认真计算即可。
7.0.75米
【分析】水面下降的体积就是圆锥体积,水槽长×宽×水面下降的高度=圆锥体积,根据圆锥的高=体积×3÷底面积,列式解答即可。
【详解】5分米=0.5米、6.28厘米=0.0628米、40厘米=0.4米
1×0.5×0.0628=0.0314(立方米)
0.0314×3÷[3.14×(0.4÷2)2]
=0.0942÷[3.14×0.22]
=0.0942÷[3.14×0.04]
=0.0942÷0.1256
=0.75(米)
答:这个圆锥形零件的高是0.75米。
【点睛】关键是掌握并灵活运用长方体和圆锥体积公式,利用转化思想,先求出圆锥体积。
8.7.5米
【分析】圆锥的体积就是沙子的体积,平铺在路上就形成了一个长方体,根据长方体体积和宽高求出铺路的长度即可。
【详解】(25×1.8÷3)÷(40×0.05)
=15÷2
=7.5(米)
答:能铺7.5米。
【点睛】本题考查圆锥、长方体的体积,解答本题的关键是掌握长方体、圆锥的体积公式。
9.(1)28.26平方米
(2)65.94立方米
【分析】(1)求蒙古包的占地面积,实际上就是求圆柱的底面积,底面直径已知,从而可以求出底面积;
(2) 蒙古包所占空间就等于圆锥与圆柱的体积和,底面直径和圆锥与圆柱的高已知,从而可以求解。
【详解】(1)3.14×(6÷2)2
=3.14×9
=28.26(平方米)
答:这个蒙古包至少占地28.26平方米。
(2)28.26×2+28.26×1×
=56.52+9.42
=65.94(立方米)
答:这个蒙古包至少占了65.94立方米的空间。
【点睛】此题主要考查圆的面积、圆锥和圆柱的体积计算方法,解答时要弄清楚有关数据的长度。
10.56.52立方分米
【分析】正方体内最大的圆锥的特点是:圆锥的底面直径和高都等于这个正方体的棱长6分米,由此利用圆锥的体积公式计算出它的体积。
【详解】×3.14×(6÷2)2×6
=×6×3.14×32
=2×3.14×9
=56.52(立方分米)
答:这个圆锥体的体积是56.52立方分米。
【点睛】这道题目主要是考查了圆锥体积公式的灵活应用,这里关键是抓住正方体内最大圆锥的特点进行解答。
11.141.3立方厘米
【分析】将圆柱的高看作单位“1”,圆柱的高×圆锥高的对应分率=圆锥的高,圆柱体积=底面积×高,圆锥体积=底面积×高÷3,陀螺的体积=圆柱体积+圆锥体积,据此列式解答。
【详解】4×=3(厘米)
3.14×32×4+3.14×32×3÷3
=113.04+28.26
=141.3(立方厘米)
答:这个陀螺的体积是141.3立方厘米。
【点睛】关键是理解分数乘法的意义,掌握并灵活运用圆柱和圆锥的体积公式。
12.圆锥;376.8立方厘米
【分析】由题意可知,以甲三角形的虚线边为轴旋转一周能形成的图形是底面半径是6厘米,高是10厘米的圆锥,根据圆锥的体积公式:V=πr2h,据此解答即可。
【详解】由分析可知:
以甲三角形的虚线边为轴旋转一周(如图2),可以形成的几何体是圆锥。
×3.14×62×10
=×113.04×10
=37.68×10
=376.8(立方厘米)
答:形成的几何体是圆锥,体积是376.8立方厘米。
【点睛】本题考查圆锥的体积,熟记公式是解题的关键。
13.62.8立方厘米
【分析】根据题意可知:以AB为轴将梯形旋转一周得到的立体图形的上面是圆锥,下面是圆柱,圆柱的底面半径是2厘米,高是4厘米,圆锥的半径是2厘米,高是(7-4)厘米,利用圆柱的体积公式V=πr2h,和圆锥的体积公式V=πr2h,分别求出它们的体积,最后再把它们加起来即可求出这个立体图形的体积是多少立方厘米。
【详解】3.14×22×4+×3.14×22×(7-4)
=3.14×4×4+×3.14×4×3
=12.56×4+×12.56×3
=50.24+×37.68
=50.24+12.56
=62.8(立方厘米)
答:这个立体图形的体积是62.8立方厘米。
【点睛】此题主要考查圆柱体和圆锥体的体积公式的应用,关键是熟记公式。
14.200.96平方厘米
【分析】由题意可知,她用同样多的橡皮泥完成了圆柱和圆锥的部分,所以圆柱和圆锥的体积相等,根据圆锥的体积公式:V=Sh,据此求出圆锥的体积即圆柱的体积,然后圆柱的体积公式:V=Sh,据此求出圆柱的底面积。
【详解】×(3.14×42×6)÷0.5
=×301.44÷0.5
=100.48÷0.5
=200.96(平方厘米)
答:圆柱部分的底面积是200.96平方厘米。
【点睛】本题考查圆柱和圆锥的体积,熟记公式是解题的关键。
15.(1)31.4平方米;
(2)不能
【分析】(1)求贴瓷砖的面积实际是求圆柱的侧面积,根据圆柱的侧面积公式:S=,代入数据,即可求出贴瓷砖的面积;
(2)先利用圆柱的体积(容积)公式:V=,代入求出圆柱形花坛的容积;先利用圆的周长公式求出圆锥的半径,再根据圆锥的体积公式:V=,求出圆锥的体积,比较泥土的体积与圆柱形花坛的容积,即可得解。
【详解】(1)3.14×20×0.5=31.4(平方米)
答:贴瓷砖的面积是31.4平方米。
(2)3.14×(20÷2)2×0.5
=3.14×102×0.5
=3.14×100×0.5
=157(立方米)
31.4÷2÷3.14=5(米)
=
=
=78.5(立方米)
157>78.5
答:这堆泥土不能填满这个花坛。
【点睛】此题的解题关键是掌握圆柱的侧面积以及圆柱和圆锥的体积公式,熟记公式,解决实际的问题。
16.188.4立方厘米
【分析】根据圆柱体积公式:V=,代入数据,求出圆柱的体积,再根据等底等高的圆柱和圆锥的体积关系,一个圆锥的体积等于与它等底等高的圆柱的体积的,求出圆锥的体积,圆柱的体积加上圆锥的体积,即是长方体的体积。
【详解】
=
=141.3(立方厘米)
141.3+141.3×
=141.3+47.1
=188.4(立方厘米)
答:长方体C的体积是188.4立方厘米。
【点睛】此题的解题关键是先求出圆柱的体积,再利用等底等高的圆柱和圆锥的体积关系,进而求出熔化后的长方体的体积。
17.(1)36分钟;(2)见详解
【分析】(1)根据圆锥的体积公式:V=,代入公式求出圆锥容器内水的体积,然后用水的体积除以水的流速,即可求出圆锥内漏完水需要的时间。
(2)因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此解答即可。
【详解】(1)×3.14×32×6÷1.57
=×3.14×9×6÷1.57
=56.52÷1.57
=36(分钟)
答:圆锥内漏完水需要36分钟。
(2)根据分析得,6×=2(厘米)
所以圆柱容器内水深2厘米。
作图如下:
【点睛】此题主要考查圆锥体积公式的灵活运用,等底等高的圆柱与圆锥体积之间的关系及应用。
18.251.2毫升
【分析】利用圆锥的容积公式:V=,代入求出圆锥容器里水的体积,再利用圆柱的容积公式:V=,代入求出圆柱的容积,用圆锥的容积减去圆柱的容积,即可得解。
【详解】×3.14×122×15-3.14×82×10
=×144×3.14×15-3.14×64×10
=48×3.14×15-200.96×10
=2260.8-2009.6
=251.2(立方厘米)
251.2立方厘米=251.2毫升
答:将有251.2毫升的水倒不下。
【点睛】此题的解题关键是灵活运用圆柱和圆锥的容积公式解决实际的问题。
19.5次
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式求出这堆沙的体积,然后根据“包含”除法的意义,用这堆沙的体积除以这辆车一次运沙的体积即可。
【详解】×3.14×(12.56÷3.14÷2)2×1.5÷1.3
=×3.14×4×1.5÷1.3
=6.28÷1.3
≈5(次)
答:要5次才能运完。
【点睛】本题主要考查整数的改写和求近似数,改写和求近似数时要注意带计数单位。
20.(1)301.44立方厘米;
(2)10厘米
【分析】(1)根据圆柱的体积公式:,计算出水的体积即可。
(2)根据圆锥的体积公式:,计算出圆锥部分的容积,用水的体积减去圆锥的容积,求出图2中圆柱部分水的体积,再除以圆柱的底面积,即可求出圆柱部分水的高度,再加上6厘米,即可求出如果将这个容器倒过来(如图2),从水面到圆锥顶点的高度是多少厘米。
【详解】(1)3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方厘米)
50.24×6=301.44(立方厘米)
答:容器中水的体积是301.44立方厘米。
(2)50.24×6×=100.48(立方厘米)
301.44-100.48=200.96(立方厘米)
200.96÷50.24=4(厘米)
4+6=10(厘米)
答:如果将这个容器倒过来(如图2),从水面到圆锥顶点的高度是10厘米。
【点睛】熟记圆柱、圆锥的体积计算公式,是解答此题的关键。
21.(1)116.68厘米(2)150.72立方米
【分析】(1)模型的高度与实际高度的比是1∶50,即模型高度是实际高度的,根据分数乘法的意义,用运载火箭的箭体全长乘就是模型的高度,再把计算结果米化成厘米即可;
(2)整流罩的圆柱部分底面直径是4米,高是10米,圆锥部分底面直径是4米,高是(16-10)米,根据圆柱体积计算公式:,圆锥体积计算公式:及半径与直径的关系:即可解答
【详解】(1)1∶50=
58.34×=1.1668(米)
1.1668米=116.68厘米
答:这一模型的高度是116.68厘米。
(2)3.14×(4÷2)2×10+3.14×(4÷2)2×(16-10)÷3
=3.14×4×10+3.14×4×6÷3
=12.56×10+12.56×6÷3
=125.6+75.36÷3
=125.6+25.12
=150.72(立方米)
答:该整流罩的容积是150.72立方米。
【点睛】本题主要考查了比的应用、圆柱和圆锥的体积,关键是记住并会熟练运用圆柱体积计算公式、圆锥体积计算公式。
22.(1)45平方厘米
(2)5616克
【分析】(1)放入圆锥形铁块,水面上升的体积就是圆锥体积,用长方体容器的长×宽×放入圆锥水面上升的高度=圆锥体积,圆锥体积×3÷高=圆锥底面积,据此分析。
(2)放入圆柱形铁块,水面上升的体积就是圆柱体积,用长方体容器的长×宽×放入圆柱水面上升的高度=圆柱体积,圆柱体积×每立方厘米铁块重量即可。
【详解】(1)20×18×0.5×3÷12
=180×3÷12
=45(平方厘米)
答:它的底面积是45平方厘米。
(2)20×18×2×7.8
=720×7.8
=5616(克)
答:这个圆柱形铁块重5616克。
【点睛】关键是利用转化思想,将圆柱和圆锥的体积转化成长方体体积进行计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
应用题专项突破:圆锥的体积-数学六年级下册北师大版
1.一个圆锥形麦堆高1.5米,底面半径是2米,如果每立方米小麦重235千克,这堆小麦重多少千克?
2.一个长方体玻璃容器从里面量,长10厘米,宽8厘米,高15厘米。里面盛有水,水中浸没着一个高为6厘米的圆锥形铅锤,把铅锤从水中取出后水面下降了0.5厘米,这个圆锥形铅锤的底面积是多少平方厘米?
3.一堆玉米堆成圆锥形,底面周长是18.84米,高是2米。
(1)如果把这些玉米装在内底面半径是2米的圆柱形粮仓里,能装多高?
(2)如果每立方米玉米重750千克,这些玉米有多少吨?
4.打谷场上有一堆圆锥形谷堆,测得谷堆的底面周长是62.8米,高是3米,要把这些稻谷分装在底面直径是2.4米,高2.5米的圆柱形粮仓里,需要多少个这样的粮仓?
5.在一个直径是2分米的圆柱形容器中,放入一个底面半径是3厘米的圆锥形铁块,全部浸没在水中,这时水面上升0.3厘米。圆锥形铁块的高是多少厘米?
6.一顶近似圆锥形的旅游帐篷,它的底面半径是4米,高是3米。
(1)按每人的活动面积为2平方米计算,每顶帐篷大约可以住几人?
(2)每顶帐篷内空间有多大?
7.有一个长方体的水槽,槽内有一个圆锥形的零件完全浸在水中,已知水槽的长为1米,宽为5分米,水面高0.5米,零件的底面直径为40厘米。当零件从水中取出后,水面下降了6.28厘米,求这个圆锥形零件的高是多少米?
8.建筑工地上有一个圆锥形的沙堆,底面积是25平方米,高是1.8米。用这堆沙在40米宽的银湖中路东段路上铺0.05米厚的路面,能铺多少米?
9.蒙古包也称“毡包”,是蒙古族传统民居。如图蒙古包是由一个圆柱体和一个圆锥体组成。
(1)这个蒙古包至少占地多大?
(2)这个蒙古包至少占了多大的空间?
10.有一块棱长6分米的正方体木料,把这块木料加工成一个最大的圆锥体。这个圆锥体的体积是多少?
11.一种深受小朋友们喜爱的玩具——陀螺(如下图)。陀螺上部分是圆柱,下部分是圆锥。圆柱的底面半径是3厘米,高4厘米;圆锥的高是圆柱高的。这个陀螺的体积是多少立方厘米?
12.把一张长10厘米、宽6厘米的长方体纸板分成两个相等的直角三角形(如图1)。以甲三角形的虚线边为轴旋转一周(如图2),可以形成的几何体是( ),请你计算出它的体积。
13.ABCD是直角梯形,以AB为轴将梯形旋转一周得到一个立体图形,这个立体图形的体积是多少立方厘米?
14.小明用橡皮泥做帽子,造型如下图。她用同样多的橡皮泥完成了圆柱和圆锥的部分,其中圆锥部分的底面半径是4厘米,高是6厘米;圆柱部分的高是0.5厘米,请你求出圆柱部分的底面积有多大。
15.社区开展文明创建,加强绿地建设,准备建造一个地面直径是20米、高0.5米的圆柱形花坛(坛壁厚度忽略不计)。
(1)如果在花坛外侧面贴上瓷砖,贴瓷砖的面积是多少平方米?
(2)现有一堆泥土,近似于一个圆锥。经测量土堆的底面周长是31.4米,高是3米。请你算一算,这堆泥土能填满这个花坛吗?
16.如图,将等底等高的两个零件圆锥A和圆柱B重新熔化,铸造成一个新的零件长方体C,已知圆柱的底面半径3厘米,高是5厘米。长方体C的体积是多少立方厘米?
17.如图30-1,这是一个由等底等高的圆柱和圆锥组合而成的计时工具,圆锥内灌满了有颜色水。其中圆锥的高为6厘米,底面半径为3厘米。已知水的流速是1.57立方厘米/分钟。
(1)圆锥内漏完水需要多少时间?
(2)请你在图30-2中用阴影表示出此时圆柱内的水。
18.一个底面半径是12厘米,高是15厘米的圆锥形容器里装满水。如果将这些水倒入一个底面半径是8厘米,高是10厘米的圆柱形容器里,将有多少毫升的水倒不下?
19.建筑师傅要将一堆圆锥形的沙土运到冬奥会建筑工地。量得沙堆底面周长12.56米,高1.5米,如果用一辆一次能运1.3立方米的汽车运,那么要多少次才能运完?
20.一个密闭玻璃容器是由一个圆柱和一个圆锥组成的,里面装有一些水(如图1,单位:厘米,玻璃的厚度忽略不计)。
(1)容器中水的体积是多少立方厘米?
(2)如果将这个容器倒过来(如图2),从水面到圆锥顶点的高度是多少厘米?
21.2022年6月5日,搭载陈冬(涧西区人)为指令长的三位航天员的“神舟十四号”载人飞船长征二号F遥十四运载火箭在酒泉卫星发射中心点火发射,发射取得圆满成功。
(1)长征二号F遥十四运载火箭的总长58.34米,小明收藏了这一型号的火箭模型,模型的高度与实际高度的比是1∶50,这一模型的高度是多少厘米?
(2)整流罩是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。下图是某型号运载火箭整流罩的简约示意图,忽略整流罩本身的厚度不计,该整流罩的容积是多少?
22.把底面积相等的一块圆锥形铁块和一块圆柱形铁块先后浸没在长是20cm、宽是18cm的盛有水的长方体容器中,先放入圆锥形铁块,水面上升了0.5cm;再放入圆柱形铁块,水面上升了2cm,没有水溢出。
(1)如果圆锥形铁块的高是12cm,那么它的底面积是多少平方厘米?
(2)如果每立方厘米铁块重7.8g,那么这个圆柱形铁块重多少克?
参考答案:
1.1475.8千克
【分析】首先根据圆锥的体积公式:V=求出沙堆的体积,然后用沙堆的体积乘每立方米小麦的质量即可。
【详解】
=6.28×235
=1475.8(千克)
答:这堆小麦重1475.8千克。
【点睛】此题考查了圆锥体积的求解方法,要注意最后不要忘记乘。
2.20平方厘米
【分析】铅锤的体积等于容器中下降部分水的体积,根据“长方体的体积=长×宽×高”求出下降部分水的体积,再利用“”求出圆锥的底面积,据此解答。
【详解】铅锤的体积:10×8×0.5
=80×0.5
=40(立方厘米)
铅锤的底面积:40×3÷6
=120÷6
=20(平方厘米)
答:这个圆锥形铅锤的底面积是20平方厘米。
【点睛】理解容器中下降部分水的体积等于圆锥的体积是解答题目的关键。
3.(1)1.5米;
(2)14.13吨
【分析】(1)由题意可知,把玉米装在圆柱形的粮仓里玉米的体积不变,先求出圆锥的底面半径,再根据“”求出这堆玉米的体积,最后利用“”求出玉米装在圆柱形粮仓里面的高度;
(2)先利用“”求出这堆玉米的体积,再乘每立方米玉米的重量求出玉米的总重量,最后把单位转化为“吨”,据此解答。
【详解】(1)18.84÷3.14÷2
=6÷2
=3(米)
=
=
=
=1.5(米)
答:能装1.5米。
(2)
=
=
=
=4500×3.14
=14130(千克)
14130千克=14.13吨
答:这些玉米有14.13吨。
【点睛】本题主要考查圆锥和圆柱体积公式的应用,熟练掌握并灵活运用公式是解答题目的关键。
4.28个
【分析】先根据圆锥的底面周长求出圆锥的底面半径,再利用“”求出这堆稻谷的体积,并利用“”求出每个圆柱形粮仓可以装稻谷的体积,需要粮仓的数量=圆锥的体积÷圆柱的体积,余下的稻谷装不满一个粮仓时需要多准备一个粮仓,结果用进一法取整数,据此解答。
【详解】62.8÷3.14÷2
=20÷2
=10(米)
=
=
=(立方米)
=
=
=(立方米)
÷≈28(个)
答:需要28个这样的粮仓。
【点睛】熟练掌握圆柱和圆锥的体积计算公式,并找出合适的取近似值的方法是解答题目的关键。
5.10厘米
【分析】水面上升的体积就是圆锥形铁块体积,根据圆柱体积公式,用容器底面积×上升的水的高度,即可求出铁块体积,再根据圆锥的高=体积×3÷底面积,列式解答即可。
【详解】2分米=20厘米
3.14×(20÷2)2×0.3×3÷(3.14×32)
=3.14×100×0.3×3÷(3.14×9)
=314×0.3×3÷28.26
=94.2×3÷28.26
=282.6÷28.26
=10(厘米)
答:圆锥形铁块的高是10厘米。
【点睛】关键是掌握并灵活运用圆柱和圆锥的体积公式。
6.(1)25人;(2)50.24立方米
【分析】(1)根据圆的面积S=πr2,求出圆锥的底面积,再除以每个人的活动面积即可。
(2)根据圆锥的体积V=πr2h,代入数据计算即可。
【详解】(1)3.14×42÷2
=50.24÷2
≈25(人)
答:每顶帐篷大约可以住25人。
(2)×3.14×42×3
=3.14×16
=50.24(立方米)
答:每顶帐篷内空间有50.24立方米。
【点睛】此题考查了有关圆锥的实际应用,明确问题所求牢记圆锥体积公式认真计算即可。
7.0.75米
【分析】水面下降的体积就是圆锥体积,水槽长×宽×水面下降的高度=圆锥体积,根据圆锥的高=体积×3÷底面积,列式解答即可。
【详解】5分米=0.5米、6.28厘米=0.0628米、40厘米=0.4米
1×0.5×0.0628=0.0314(立方米)
0.0314×3÷[3.14×(0.4÷2)2]
=0.0942÷[3.14×0.22]
=0.0942÷[3.14×0.04]
=0.0942÷0.1256
=0.75(米)
答:这个圆锥形零件的高是0.75米。
【点睛】关键是掌握并灵活运用长方体和圆锥体积公式,利用转化思想,先求出圆锥体积。
8.7.5米
【分析】圆锥的体积就是沙子的体积,平铺在路上就形成了一个长方体,根据长方体体积和宽高求出铺路的长度即可。
【详解】(25×1.8÷3)÷(40×0.05)
=15÷2
=7.5(米)
答:能铺7.5米。
【点睛】本题考查圆锥、长方体的体积,解答本题的关键是掌握长方体、圆锥的体积公式。
9.(1)28.26平方米
(2)65.94立方米
【分析】(1)求蒙古包的占地面积,实际上就是求圆柱的底面积,底面直径已知,从而可以求出底面积;
(2) 蒙古包所占空间就等于圆锥与圆柱的体积和,底面直径和圆锥与圆柱的高已知,从而可以求解。
【详解】(1)3.14×(6÷2)2
=3.14×9
=28.26(平方米)
答:这个蒙古包至少占地28.26平方米。
(2)28.26×2+28.26×1×
=56.52+9.42
=65.94(立方米)
答:这个蒙古包至少占了65.94立方米的空间。
【点睛】此题主要考查圆的面积、圆锥和圆柱的体积计算方法,解答时要弄清楚有关数据的长度。
10.56.52立方分米
【分析】正方体内最大的圆锥的特点是:圆锥的底面直径和高都等于这个正方体的棱长6分米,由此利用圆锥的体积公式计算出它的体积。
【详解】×3.14×(6÷2)2×6
=×6×3.14×32
=2×3.14×9
=56.52(立方分米)
答:这个圆锥体的体积是56.52立方分米。
【点睛】这道题目主要是考查了圆锥体积公式的灵活应用,这里关键是抓住正方体内最大圆锥的特点进行解答。
11.141.3立方厘米
【分析】将圆柱的高看作单位“1”,圆柱的高×圆锥高的对应分率=圆锥的高,圆柱体积=底面积×高,圆锥体积=底面积×高÷3,陀螺的体积=圆柱体积+圆锥体积,据此列式解答。
【详解】4×=3(厘米)
3.14×32×4+3.14×32×3÷3
=113.04+28.26
=141.3(立方厘米)
答:这个陀螺的体积是141.3立方厘米。
【点睛】关键是理解分数乘法的意义,掌握并灵活运用圆柱和圆锥的体积公式。
12.圆锥;376.8立方厘米
【分析】由题意可知,以甲三角形的虚线边为轴旋转一周能形成的图形是底面半径是6厘米,高是10厘米的圆锥,根据圆锥的体积公式:V=πr2h,据此解答即可。
【详解】由分析可知:
以甲三角形的虚线边为轴旋转一周(如图2),可以形成的几何体是圆锥。
×3.14×62×10
=×113.04×10
=37.68×10
=376.8(立方厘米)
答:形成的几何体是圆锥,体积是376.8立方厘米。
【点睛】本题考查圆锥的体积,熟记公式是解题的关键。
13.62.8立方厘米
【分析】根据题意可知:以AB为轴将梯形旋转一周得到的立体图形的上面是圆锥,下面是圆柱,圆柱的底面半径是2厘米,高是4厘米,圆锥的半径是2厘米,高是(7-4)厘米,利用圆柱的体积公式V=πr2h,和圆锥的体积公式V=πr2h,分别求出它们的体积,最后再把它们加起来即可求出这个立体图形的体积是多少立方厘米。
【详解】3.14×22×4+×3.14×22×(7-4)
=3.14×4×4+×3.14×4×3
=12.56×4+×12.56×3
=50.24+×37.68
=50.24+12.56
=62.8(立方厘米)
答:这个立体图形的体积是62.8立方厘米。
【点睛】此题主要考查圆柱体和圆锥体的体积公式的应用,关键是熟记公式。
14.200.96平方厘米
【分析】由题意可知,她用同样多的橡皮泥完成了圆柱和圆锥的部分,所以圆柱和圆锥的体积相等,根据圆锥的体积公式:V=Sh,据此求出圆锥的体积即圆柱的体积,然后圆柱的体积公式:V=Sh,据此求出圆柱的底面积。
【详解】×(3.14×42×6)÷0.5
=×301.44÷0.5
=100.48÷0.5
=200.96(平方厘米)
答:圆柱部分的底面积是200.96平方厘米。
【点睛】本题考查圆柱和圆锥的体积,熟记公式是解题的关键。
15.(1)31.4平方米;
(2)不能
【分析】(1)求贴瓷砖的面积实际是求圆柱的侧面积,根据圆柱的侧面积公式:S=,代入数据,即可求出贴瓷砖的面积;
(2)先利用圆柱的体积(容积)公式:V=,代入求出圆柱形花坛的容积;先利用圆的周长公式求出圆锥的半径,再根据圆锥的体积公式:V=,求出圆锥的体积,比较泥土的体积与圆柱形花坛的容积,即可得解。
【详解】(1)3.14×20×0.5=31.4(平方米)
答:贴瓷砖的面积是31.4平方米。
(2)3.14×(20÷2)2×0.5
=3.14×102×0.5
=3.14×100×0.5
=157(立方米)
31.4÷2÷3.14=5(米)
=
=
=78.5(立方米)
157>78.5
答:这堆泥土不能填满这个花坛。
【点睛】此题的解题关键是掌握圆柱的侧面积以及圆柱和圆锥的体积公式,熟记公式,解决实际的问题。
16.188.4立方厘米
【分析】根据圆柱体积公式:V=,代入数据,求出圆柱的体积,再根据等底等高的圆柱和圆锥的体积关系,一个圆锥的体积等于与它等底等高的圆柱的体积的,求出圆锥的体积,圆柱的体积加上圆锥的体积,即是长方体的体积。
【详解】
=
=141.3(立方厘米)
141.3+141.3×
=141.3+47.1
=188.4(立方厘米)
答:长方体C的体积是188.4立方厘米。
【点睛】此题的解题关键是先求出圆柱的体积,再利用等底等高的圆柱和圆锥的体积关系,进而求出熔化后的长方体的体积。
17.(1)36分钟;(2)见详解
【分析】(1)根据圆锥的体积公式:V=,代入公式求出圆锥容器内水的体积,然后用水的体积除以水的流速,即可求出圆锥内漏完水需要的时间。
(2)因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此解答即可。
【详解】(1)×3.14×32×6÷1.57
=×3.14×9×6÷1.57
=56.52÷1.57
=36(分钟)
答:圆锥内漏完水需要36分钟。
(2)根据分析得,6×=2(厘米)
所以圆柱容器内水深2厘米。
作图如下:
【点睛】此题主要考查圆锥体积公式的灵活运用,等底等高的圆柱与圆锥体积之间的关系及应用。
18.251.2毫升
【分析】利用圆锥的容积公式:V=,代入求出圆锥容器里水的体积,再利用圆柱的容积公式:V=,代入求出圆柱的容积,用圆锥的容积减去圆柱的容积,即可得解。
【详解】×3.14×122×15-3.14×82×10
=×144×3.14×15-3.14×64×10
=48×3.14×15-200.96×10
=2260.8-2009.6
=251.2(立方厘米)
251.2立方厘米=251.2毫升
答:将有251.2毫升的水倒不下。
【点睛】此题的解题关键是灵活运用圆柱和圆锥的容积公式解决实际的问题。
19.5次
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式求出这堆沙的体积,然后根据“包含”除法的意义,用这堆沙的体积除以这辆车一次运沙的体积即可。
【详解】×3.14×(12.56÷3.14÷2)2×1.5÷1.3
=×3.14×4×1.5÷1.3
=6.28÷1.3
≈5(次)
答:要5次才能运完。
【点睛】本题主要考查整数的改写和求近似数,改写和求近似数时要注意带计数单位。
20.(1)301.44立方厘米;
(2)10厘米
【分析】(1)根据圆柱的体积公式:,计算出水的体积即可。
(2)根据圆锥的体积公式:,计算出圆锥部分的容积,用水的体积减去圆锥的容积,求出图2中圆柱部分水的体积,再除以圆柱的底面积,即可求出圆柱部分水的高度,再加上6厘米,即可求出如果将这个容器倒过来(如图2),从水面到圆锥顶点的高度是多少厘米。
【详解】(1)3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方厘米)
50.24×6=301.44(立方厘米)
答:容器中水的体积是301.44立方厘米。
(2)50.24×6×=100.48(立方厘米)
301.44-100.48=200.96(立方厘米)
200.96÷50.24=4(厘米)
4+6=10(厘米)
答:如果将这个容器倒过来(如图2),从水面到圆锥顶点的高度是10厘米。
【点睛】熟记圆柱、圆锥的体积计算公式,是解答此题的关键。
21.(1)116.68厘米(2)150.72立方米
【分析】(1)模型的高度与实际高度的比是1∶50,即模型高度是实际高度的,根据分数乘法的意义,用运载火箭的箭体全长乘就是模型的高度,再把计算结果米化成厘米即可;
(2)整流罩的圆柱部分底面直径是4米,高是10米,圆锥部分底面直径是4米,高是(16-10)米,根据圆柱体积计算公式:,圆锥体积计算公式:及半径与直径的关系:即可解答
【详解】(1)1∶50=
58.34×=1.1668(米)
1.1668米=116.68厘米
答:这一模型的高度是116.68厘米。
(2)3.14×(4÷2)2×10+3.14×(4÷2)2×(16-10)÷3
=3.14×4×10+3.14×4×6÷3
=12.56×10+12.56×6÷3
=125.6+75.36÷3
=125.6+25.12
=150.72(立方米)
答:该整流罩的容积是150.72立方米。
【点睛】本题主要考查了比的应用、圆柱和圆锥的体积,关键是记住并会熟练运用圆柱体积计算公式、圆锥体积计算公式。
22.(1)45平方厘米
(2)5616克
【分析】(1)放入圆锥形铁块,水面上升的体积就是圆锥体积,用长方体容器的长×宽×放入圆锥水面上升的高度=圆锥体积,圆锥体积×3÷高=圆锥底面积,据此分析。
(2)放入圆柱形铁块,水面上升的体积就是圆柱体积,用长方体容器的长×宽×放入圆柱水面上升的高度=圆柱体积,圆柱体积×每立方厘米铁块重量即可。
【详解】(1)20×18×0.5×3÷12
=180×3÷12
=45(平方厘米)
答:它的底面积是45平方厘米。
(2)20×18×2×7.8
=720×7.8
=5616(克)
答:这个圆柱形铁块重5616克。
【点睛】关键是利用转化思想,将圆柱和圆锥的体积转化成长方体体积进行计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
