圆锥的体积应用题经典题型提升卷(含答案)数学六年级下册北师大版
文档属性
| 名称 | 圆锥的体积应用题经典题型提升卷(含答案)数学六年级下册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 372.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
圆锥的体积应用题经典题型(提升卷)数学六年级下册北师大版
1.一个圆锥形小麦堆的底面周长为12.56m,高是3m。如果每立方米小麦的质量为700kg,这堆小麦的质量为多少千克?
2.芳芳在一个底面半径是6cm,高是15cm的圆柱形玻璃杯内装入10cm高的水,然后放入一个底面直径是8cm的圆锥形铅锤(完全浸没),水面上升到11.6cm,这个铅锤的高是多少厘米?
3.一个圆锥形沙滩,底面积是28.26 m2,高是2.5m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
4.一个圆锥形钢块,量得它的体积是157立方厘米,底面直径是5厘米。它的高是多少厘米?
5.一个圆柱形玻璃容器里装有水,水中浸没着一个底面直径为6cm,高为10 cm的圆锥形铁块(如右图)。
(1)这个铁块的体积是多少?
(2)如果把铁块从水中取出,那么容器中的水面高度将下降多少cm?
6.把一个底面半径是4厘米,高是6厘米的铁制圆锥体放入盛满水的桶里,将有多少立方厘米的水溢出?
7.某地新建一个圆柱形粮囤,从外面测,粮囤的直径为8米,高为60分米。
(1)这个粮囤占地多少平方米
(2)现在要将粮囤外墙面全部粉刷成白色,粉刷面积是多少平方米
(3)有一堆玉米,堆成近似圆锥形,底面周长是37.68米,高是6米,要把这些玉米全部装入粮囤,正好装满一半,这个粮囤的容积是多少
8.一个圆锥形的麦堆,底面半径是3米,高是2米。如果把这些小麦装入一个圆柱形粮囤,只占粮囤容积的 。已知粮囤的底面积是9平方米,粮囤的高是多少米?
9.一个圆锥形砂堆,底面周长是31.4米,高3米,每方砂重1.8吨,用一辆载重4.5吨的汽车,几次可以运完?(得数保留整数)
10.一个底面半径是4厘米的圆锥形木块,从顶点处垂直于底面把它切成两个完全相等的木块,这时表面积增加了48平方厘米。这个木块原来的体积是多少立方厘米?
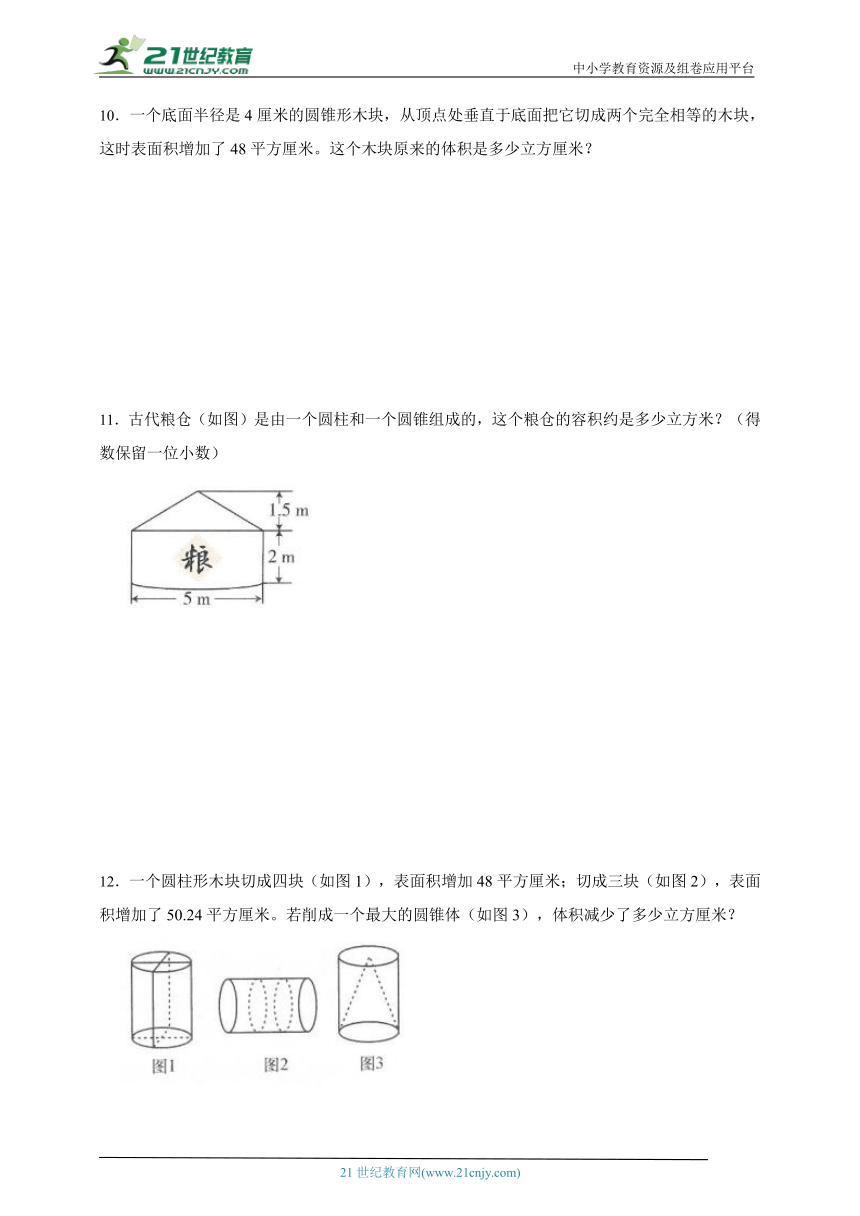
11.古代粮仓(如图)是由一个圆柱和一个圆锥组成的,这个粮仓的容积约是多少立方米?(得数保留一位小数)
12.一个圆柱形木块切成四块(如图1),表面积增加48平方厘米;切成三块(如图2),表面积增加了50.24平方厘米。若削成一个最大的圆锥体(如图3),体积减少了多少立方厘米?
13.下列直角三角形,沿一条直角边旋转一周,会得到一个,通过计算说明怎么旋转得到的体积大。
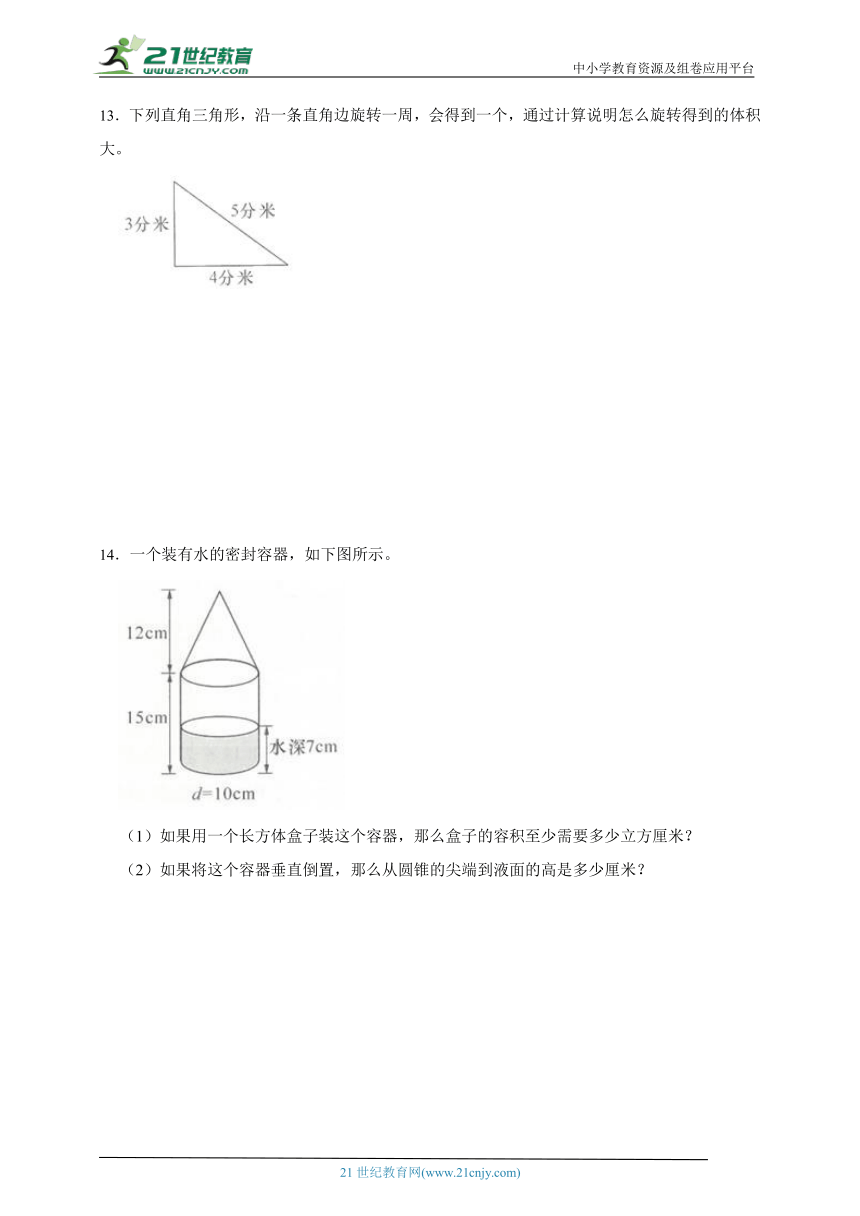
14.一个装有水的密封容器,如下图所示。
(1)如果用一个长方体盒子装这个容器,那么盒子的容积至少需要多少立方厘米?
(2)如果将这个容器垂直倒置,那么从圆锥的尖端到液面的高是多少厘米?
15.有一段底面半径是8分米,高6分米的圆柱形钢材,现把它熔铸成一个高是3分米的圆锥体,圆锥的底面积是多少平方分米
16.一个圆锥的底面周长是15.7厘米,高是3厘米.从圆锥的顶点沿着高将它切成两半后,表面积之和比原圆锥的表面积增加了多少平方厘米?
17.圆锥的高和底面半径都等于一个正方体的棱长,已知正方体的体积是27立方厘米,这个圆锥的体积是多少立方厘米?
18.如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?(单位:厘米)(π=3.14)
答案解析部分
1.【答案】解:半径:12.56÷3.14÷2
=4÷2
=2(米)
×3.14×22×3×700
=3.14×4×(×3)×700
=12.56×700
=8792(千克)
答:这堆小麦的质量为8792千克。
2.【答案】解:圆锥的体积:
3.14×62×(11.6-10)
=3.14×36×1.6
=180.864(cm3)
180.864×3÷[3.14×(8÷2)2]
=542.592÷50.24
=10.8(厘米)
答:这个铅锤的高是10.8厘米。
3.【答案】解: ×28.26×2.5÷(10×0.02)
=23.55÷0.2
=117.75(米)
答:能铺117.5米。
4.【答案】解:5厘米÷2=2.5厘米,
3.14×2.5×2.5=19.625(平方厘米)
157×3÷19.625=471÷19.625=24(厘米)
答:它的高是24厘米。
5.【答案】(1)解:6÷2=3(cm)
3.14×32×10×
=3.14×(9×)×10
=3.14×3×10
=9.42×10
=94.2(cm3)
答:这个铁块的体积是94.2cm3。
(2)解:10÷2=5(cm)
94.2÷3.14÷52
=30÷25
=1.2(cm)
答:容器中的水面高度将下降1.2cm。
6.【答案】解:3.14×42×6×
=3.14×16×(6×)
=3.14×16×2
=50.24×2
=100.48(立方厘米)
答:将有100.48立方厘米的水溢出。
7.【答案】(1)解:3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方米)
答: 这个粮囤占地50.24平方米 。
(2)解:60分米=6米
3.14×8×6
=3.14×48
=150.72(平方米)
答: 粉刷面积是150.72平方米 。
(3)解:玉米的体积:3.14×(37.68÷3.14÷2)2×6×
=3.14×(12÷2)2×2
=3.14×62×2
=3.14×72
=226.08(立方米)
226.08×2=452.16(立方米)
答: 这个粮囤的容积是 452.16立方米。
8.【答案】解:3.14×3×3××2
=9.42×3××2
=28.26××2
=9.42×2
=18.84(m3)
18.84÷÷9
=42.39÷9
=4.71(m)
答:粮囤的高是4.71m。
9.【答案】解:31.4÷3.14÷2
=10÷2
=5(米)
3.14×52×3×
=(3.14×25)×(3×)
=78.5×1
=78.5(立方米)
78.5×1.8÷4.5
=141.3÷4.5
≈32(次)
答:32次可以运完。
10.【答案】48÷2×2÷(4×2)=6(厘米)
×3.14×42×6=100.48(立方厘米)
答:这个木块原来的体积是100.48立方厘米。
11.【答案】解:3.14×(5÷2)2×2+3.14×(5÷2)2×1.5×
=3.14×6.25×2+3.14×6.25×0.5
=3.14×6.25×(2+0.5)
=19.625×2.5
≈49.1(立方米)
答:这个粮仓的容积约是49.1立方米。
12.【答案】解:50.24÷4÷3.14
=12.56÷3.14
=4
因为2×2=4,所以圆柱体的底面圆半径为2厘米,
48÷8÷2=3(厘米)
圆柱体的高为3厘米,
3.14×22×3×
=3.14×8
=25.12(立方厘米)
答:体积减少了25.12立方厘米。
13.【答案】解: ×3.14×42×3= ×3.14×16×3=50.24(立方分米);
×3.14×32×4= ×3.14×9×4=37.68(立方分米);
50.24>37.68,
答:沿3分米的直角边旋转,得到一个底面半径是4分米,高3分米的圆锥的体积较大。
14.【答案】(1)解:由图可知长方体盒子的长宽高至少是长为10cm,宽为10cm,高为15+12=27cm。
V盒=10×10×27=2700(cm3)
答:那么盒子的容积至少需要2700立方厘米。
(2)解:V水= r2h=3.14×(10÷2)2×7=549.5(cm3)
S底= r2=3.14×(10÷2)2=78.5(cm2)
V锥= S底h= ×78.5×12=314(cm3)
549.5-314=235.5(cm3)
235.5÷78.5=3(cm)
12+3=15(cm)
答:从圆锥的尖端到液面的高是15厘米。
15.【答案】解:圆柱的体积:3.14×82×6=1205.76(立方分米)
圆锥的底面积:1205.76÷÷3=1205.76(平方分米)
答:圆锥的底面积是1205.76平方分米。
16.【答案】解:圆锥的底面直径为:15.7÷3.14=5(厘米)
则切割后表面积增加了:5×3÷2×2=15(平方厘米)
答:表面积之和比原来圆锥表面积增加15平方厘米。
17.【答案】解:33=27,所以正方体的棱长是3厘米.
=
=28.26(立方厘米)
答:这个圆锥的体积是28.26立方厘米。
18.【答案】解:12÷3=4(厘米)
答:乙容器中的水有4厘米高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆锥的体积应用题经典题型(提升卷)数学六年级下册北师大版
1.一个圆锥形小麦堆的底面周长为12.56m,高是3m。如果每立方米小麦的质量为700kg,这堆小麦的质量为多少千克?
2.芳芳在一个底面半径是6cm,高是15cm的圆柱形玻璃杯内装入10cm高的水,然后放入一个底面直径是8cm的圆锥形铅锤(完全浸没),水面上升到11.6cm,这个铅锤的高是多少厘米?
3.一个圆锥形沙滩,底面积是28.26 m2,高是2.5m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
4.一个圆锥形钢块,量得它的体积是157立方厘米,底面直径是5厘米。它的高是多少厘米?
5.一个圆柱形玻璃容器里装有水,水中浸没着一个底面直径为6cm,高为10 cm的圆锥形铁块(如右图)。
(1)这个铁块的体积是多少?
(2)如果把铁块从水中取出,那么容器中的水面高度将下降多少cm?
6.把一个底面半径是4厘米,高是6厘米的铁制圆锥体放入盛满水的桶里,将有多少立方厘米的水溢出?
7.某地新建一个圆柱形粮囤,从外面测,粮囤的直径为8米,高为60分米。
(1)这个粮囤占地多少平方米
(2)现在要将粮囤外墙面全部粉刷成白色,粉刷面积是多少平方米
(3)有一堆玉米,堆成近似圆锥形,底面周长是37.68米,高是6米,要把这些玉米全部装入粮囤,正好装满一半,这个粮囤的容积是多少
8.一个圆锥形的麦堆,底面半径是3米,高是2米。如果把这些小麦装入一个圆柱形粮囤,只占粮囤容积的 。已知粮囤的底面积是9平方米,粮囤的高是多少米?
9.一个圆锥形砂堆,底面周长是31.4米,高3米,每方砂重1.8吨,用一辆载重4.5吨的汽车,几次可以运完?(得数保留整数)
10.一个底面半径是4厘米的圆锥形木块,从顶点处垂直于底面把它切成两个完全相等的木块,这时表面积增加了48平方厘米。这个木块原来的体积是多少立方厘米?
11.古代粮仓(如图)是由一个圆柱和一个圆锥组成的,这个粮仓的容积约是多少立方米?(得数保留一位小数)
12.一个圆柱形木块切成四块(如图1),表面积增加48平方厘米;切成三块(如图2),表面积增加了50.24平方厘米。若削成一个最大的圆锥体(如图3),体积减少了多少立方厘米?
13.下列直角三角形,沿一条直角边旋转一周,会得到一个,通过计算说明怎么旋转得到的体积大。
14.一个装有水的密封容器,如下图所示。
(1)如果用一个长方体盒子装这个容器,那么盒子的容积至少需要多少立方厘米?
(2)如果将这个容器垂直倒置,那么从圆锥的尖端到液面的高是多少厘米?
15.有一段底面半径是8分米,高6分米的圆柱形钢材,现把它熔铸成一个高是3分米的圆锥体,圆锥的底面积是多少平方分米
16.一个圆锥的底面周长是15.7厘米,高是3厘米.从圆锥的顶点沿着高将它切成两半后,表面积之和比原圆锥的表面积增加了多少平方厘米?
17.圆锥的高和底面半径都等于一个正方体的棱长,已知正方体的体积是27立方厘米,这个圆锥的体积是多少立方厘米?
18.如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?(单位:厘米)(π=3.14)
答案解析部分
1.【答案】解:半径:12.56÷3.14÷2
=4÷2
=2(米)
×3.14×22×3×700
=3.14×4×(×3)×700
=12.56×700
=8792(千克)
答:这堆小麦的质量为8792千克。
2.【答案】解:圆锥的体积:
3.14×62×(11.6-10)
=3.14×36×1.6
=180.864(cm3)
180.864×3÷[3.14×(8÷2)2]
=542.592÷50.24
=10.8(厘米)
答:这个铅锤的高是10.8厘米。
3.【答案】解: ×28.26×2.5÷(10×0.02)
=23.55÷0.2
=117.75(米)
答:能铺117.5米。
4.【答案】解:5厘米÷2=2.5厘米,
3.14×2.5×2.5=19.625(平方厘米)
157×3÷19.625=471÷19.625=24(厘米)
答:它的高是24厘米。
5.【答案】(1)解:6÷2=3(cm)
3.14×32×10×
=3.14×(9×)×10
=3.14×3×10
=9.42×10
=94.2(cm3)
答:这个铁块的体积是94.2cm3。
(2)解:10÷2=5(cm)
94.2÷3.14÷52
=30÷25
=1.2(cm)
答:容器中的水面高度将下降1.2cm。
6.【答案】解:3.14×42×6×
=3.14×16×(6×)
=3.14×16×2
=50.24×2
=100.48(立方厘米)
答:将有100.48立方厘米的水溢出。
7.【答案】(1)解:3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方米)
答: 这个粮囤占地50.24平方米 。
(2)解:60分米=6米
3.14×8×6
=3.14×48
=150.72(平方米)
答: 粉刷面积是150.72平方米 。
(3)解:玉米的体积:3.14×(37.68÷3.14÷2)2×6×
=3.14×(12÷2)2×2
=3.14×62×2
=3.14×72
=226.08(立方米)
226.08×2=452.16(立方米)
答: 这个粮囤的容积是 452.16立方米。
8.【答案】解:3.14×3×3××2
=9.42×3××2
=28.26××2
=9.42×2
=18.84(m3)
18.84÷÷9
=42.39÷9
=4.71(m)
答:粮囤的高是4.71m。
9.【答案】解:31.4÷3.14÷2
=10÷2
=5(米)
3.14×52×3×
=(3.14×25)×(3×)
=78.5×1
=78.5(立方米)
78.5×1.8÷4.5
=141.3÷4.5
≈32(次)
答:32次可以运完。
10.【答案】48÷2×2÷(4×2)=6(厘米)
×3.14×42×6=100.48(立方厘米)
答:这个木块原来的体积是100.48立方厘米。
11.【答案】解:3.14×(5÷2)2×2+3.14×(5÷2)2×1.5×
=3.14×6.25×2+3.14×6.25×0.5
=3.14×6.25×(2+0.5)
=19.625×2.5
≈49.1(立方米)
答:这个粮仓的容积约是49.1立方米。
12.【答案】解:50.24÷4÷3.14
=12.56÷3.14
=4
因为2×2=4,所以圆柱体的底面圆半径为2厘米,
48÷8÷2=3(厘米)
圆柱体的高为3厘米,
3.14×22×3×
=3.14×8
=25.12(立方厘米)
答:体积减少了25.12立方厘米。
13.【答案】解: ×3.14×42×3= ×3.14×16×3=50.24(立方分米);
×3.14×32×4= ×3.14×9×4=37.68(立方分米);
50.24>37.68,
答:沿3分米的直角边旋转,得到一个底面半径是4分米,高3分米的圆锥的体积较大。
14.【答案】(1)解:由图可知长方体盒子的长宽高至少是长为10cm,宽为10cm,高为15+12=27cm。
V盒=10×10×27=2700(cm3)
答:那么盒子的容积至少需要2700立方厘米。
(2)解:V水= r2h=3.14×(10÷2)2×7=549.5(cm3)
S底= r2=3.14×(10÷2)2=78.5(cm2)
V锥= S底h= ×78.5×12=314(cm3)
549.5-314=235.5(cm3)
235.5÷78.5=3(cm)
12+3=15(cm)
答:从圆锥的尖端到液面的高是15厘米。
15.【答案】解:圆柱的体积:3.14×82×6=1205.76(立方分米)
圆锥的底面积:1205.76÷÷3=1205.76(平方分米)
答:圆锥的底面积是1205.76平方分米。
16.【答案】解:圆锥的底面直径为:15.7÷3.14=5(厘米)
则切割后表面积增加了:5×3÷2×2=15(平方厘米)
答:表面积之和比原来圆锥表面积增加15平方厘米。
17.【答案】解:33=27,所以正方体的棱长是3厘米.
=
=28.26(立方厘米)
答:这个圆锥的体积是28.26立方厘米。
18.【答案】解:12÷3=4(厘米)
答:乙容器中的水有4厘米高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
