6.4生活中的圆周运动课件-2023-2024学年高一下学期物理人教版(2019)必修第二册(共22张PPT)
文档属性
| 名称 | 6.4生活中的圆周运动课件-2023-2024学年高一下学期物理人教版(2019)必修第二册(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 46.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
第六章:第四节
生活中的圆周
运动
新课导入
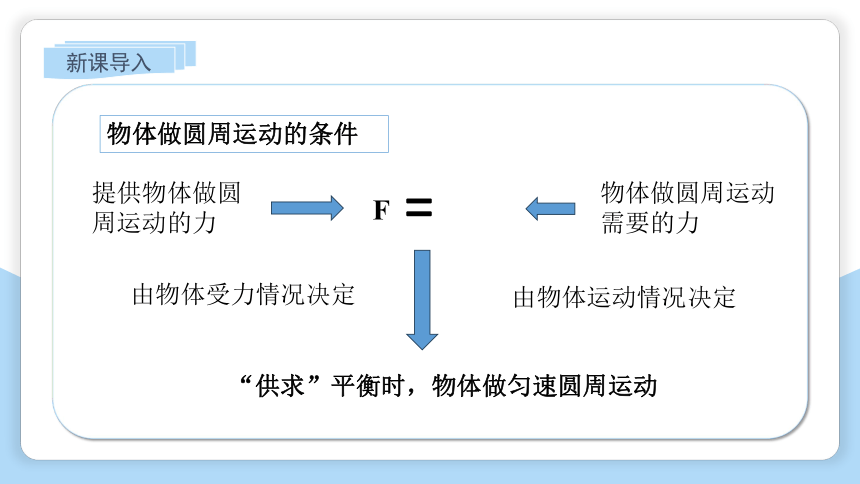
物体做圆周运动的条件
提供物体做圆周运动的力
F
物体做圆周运动需要的力
由物体受力情况决定
由物体运动情况决定
“供求”平衡时,物体做匀速圆周运动
=
火车转弯
外轨
内轨
G
FN
F
所需向心力由什么力提供?
外轨对轮缘的弹力
内外轨道等高时转弯
火车转弯
问题与思考:在铁路弯道处,为什么外高内低?为什么这样设计呢?
θ
FN
G
F合
θ
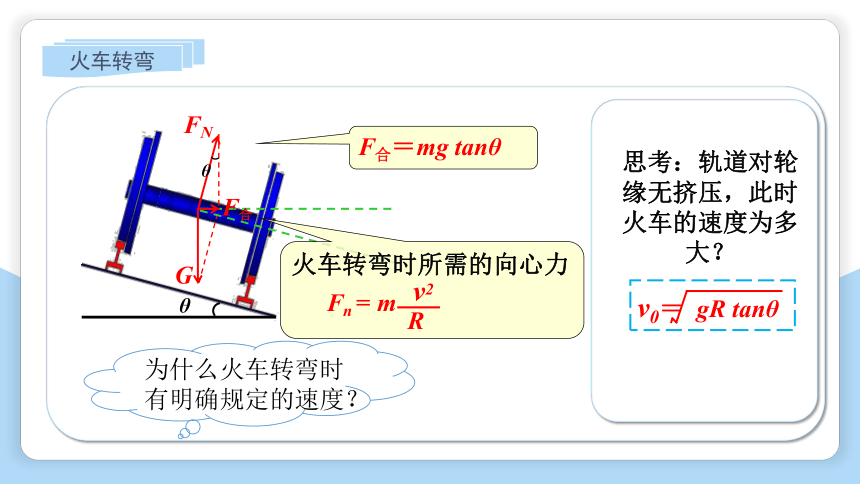
火车转弯
F合=mg tanθ
火车转弯时所需的向心力
Fn = m
v2
R
思考:轨道对轮缘无挤压,此时火车的速度为多大?
v0= gR tanθ
为什么火车转弯时有明确规定的速度?
当 v> gR tan θ
G
FN
θ
轮缘受到外轨向内的弹力
挤压外轨
G
FN
θ
F
F
轮缘受到内轨向外的弹力
挤压内轨
火车转弯
当 v> v0
当 v< v0
巩固提升
如图所示,在修筑铁路时,弯道处的外轨会略高于内轨。当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时火车的速度大小为v,重力加速度为g,两轨所在平面的倾角为θ,则下列说法不正确的是
A.该弯道的半径r=
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于v时,内轨将受到轮缘的挤压
D.当火车以规定的行驶速度转弯时,向心加速度大小为an=gtan θ
C
汽车过拱形桥
汽车过拱形桥
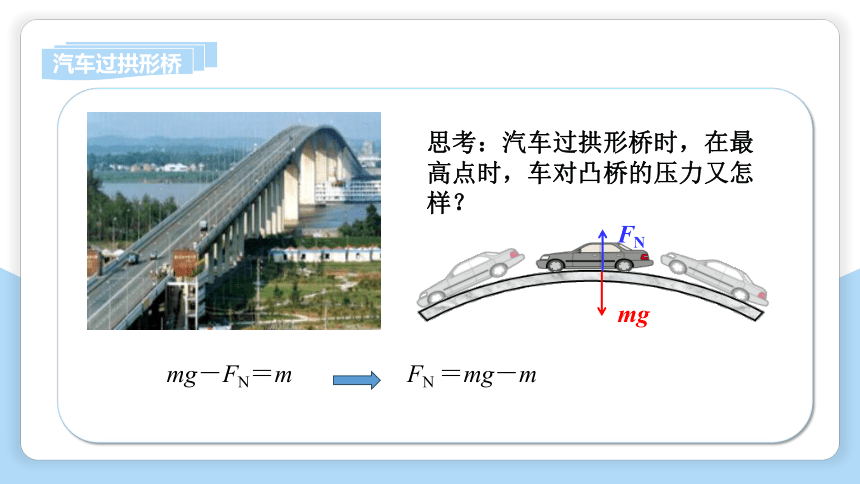
思考:汽车过拱形桥时,在最高点时,车对凸桥的压力又怎样?
mg
FN
mg-FN=m
FN =mg-m
v2
R
mg=m
思考:当 FN = 0 时,汽车会做什么运动,此时汽车的速度多大?
v2
R
FN =mg-m
思考:汽车过拱形桥时,运动速度变大,车对拱桥的压力如何变化?
mg
FN
临界速度
汽车过拱形桥
汽车过拱形桥
思考:汽车过凹形桥在最低点时,车对凹形桥的压力又怎样?
FN-mg=m
FN =mg + m
FN
mg
思考:当速度逐渐增大,小车会怎么样?
v2
R
FN =mg + m
思考:汽车过拱形桥时,运动速度变大,车对拱桥的压力如何变化?
mg
FN
汽车过拱形桥
爆胎
FN =mg-m
FN =mg-m
FN =mg
失重
超重
汽车过拱形桥
巩固提升
如图所示,一汽车在某次性能测试中需通过一半径拱桥,要求汽车经过最高点时不能离开桥面,取,时的速度符合要求的是( )
A.20km/h B.30km/h C.40km/h D.50km/h
ABC
思考1:航天器在发射升空(加速上升)时,航天员处在超重还是失重状态?
思考2:航天器在轨道正常运行(绕地球做匀速圆周运动)时,航天员处在超重还是失重状态?
FN
mg
a
FN-mg =ma
FN>mg
航天器绕地球做匀速圆周运动,假设它的线速度的大小为v ,轨道半径近似等于地球半径R ,航天员受到的地球引力近似等于他在地面测得的体重mg 。
v2
R
FN =mg-m
FN <mg
当 时,座舱对航天员的支持力FN=0 ,航天员处于完全失重.
如果地球的引力突然消失,航天器将做什么样的运动呢?
离心运动
思考:为什么铁球与橡皮泥会飞出去?
定义:做圆周运动的物体,在其所受合外力突然消失,或不足以提供圆周运动所需向心力的情况下,就做逐渐远离圆心的运动,这种运动叫作离心运动。
做离心运动的条件:
离心运动
离心运动的应用
离心运动的防止
规律总结
F 合= 0 ,物体沿切线方向飞出远离圆心
F合<mω2r ,物体做逐渐远离圆心的运动
F合 = mω2r,物体做匀速圆周运动
F合>mω2r ,物体做逐渐靠近圆心的运动
巩固提升
在水平公路上行驶的汽车,当汽车以一定速度运动时,车轮与路面间的最大静摩擦力恰好等于汽车转弯所需要的向心力,汽车沿如图所示的圆形路径(虚线)运动,当汽车行驶速度突然增大,则汽车的运动路径可能是
A.Ⅰ B.Ⅱ C.Ⅲ D.Ⅳ
B
第六章:第四节
生活中的圆周
运动
新课导入
物体做圆周运动的条件
提供物体做圆周运动的力
F
物体做圆周运动需要的力
由物体受力情况决定
由物体运动情况决定
“供求”平衡时,物体做匀速圆周运动
=
火车转弯
外轨
内轨
G
FN
F
所需向心力由什么力提供?
外轨对轮缘的弹力
内外轨道等高时转弯
火车转弯
问题与思考:在铁路弯道处,为什么外高内低?为什么这样设计呢?
θ
FN
G
F合
θ
火车转弯
F合=mg tanθ
火车转弯时所需的向心力
Fn = m
v2
R
思考:轨道对轮缘无挤压,此时火车的速度为多大?
v0= gR tanθ
为什么火车转弯时有明确规定的速度?
当 v> gR tan θ
G
FN
θ
轮缘受到外轨向内的弹力
挤压外轨
G
FN
θ
F
F
轮缘受到内轨向外的弹力
挤压内轨
火车转弯
当 v> v0
当 v< v0
巩固提升
如图所示,在修筑铁路时,弯道处的外轨会略高于内轨。当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时火车的速度大小为v,重力加速度为g,两轨所在平面的倾角为θ,则下列说法不正确的是
A.该弯道的半径r=
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于v时,内轨将受到轮缘的挤压
D.当火车以规定的行驶速度转弯时,向心加速度大小为an=gtan θ
C
汽车过拱形桥
汽车过拱形桥
思考:汽车过拱形桥时,在最高点时,车对凸桥的压力又怎样?
mg
FN
mg-FN=m
FN =mg-m
v2
R
mg=m
思考:当 FN = 0 时,汽车会做什么运动,此时汽车的速度多大?
v2
R
FN =mg-m
思考:汽车过拱形桥时,运动速度变大,车对拱桥的压力如何变化?
mg
FN
临界速度
汽车过拱形桥
汽车过拱形桥
思考:汽车过凹形桥在最低点时,车对凹形桥的压力又怎样?
FN-mg=m
FN =mg + m
FN
mg
思考:当速度逐渐增大,小车会怎么样?
v2
R
FN =mg + m
思考:汽车过拱形桥时,运动速度变大,车对拱桥的压力如何变化?
mg
FN
汽车过拱形桥
爆胎
FN =mg-m
FN =mg-m
FN =mg
失重
超重
汽车过拱形桥
巩固提升
如图所示,一汽车在某次性能测试中需通过一半径拱桥,要求汽车经过最高点时不能离开桥面,取,时的速度符合要求的是( )
A.20km/h B.30km/h C.40km/h D.50km/h
ABC
思考1:航天器在发射升空(加速上升)时,航天员处在超重还是失重状态?
思考2:航天器在轨道正常运行(绕地球做匀速圆周运动)时,航天员处在超重还是失重状态?
FN
mg
a
FN-mg =ma
FN>mg
航天器绕地球做匀速圆周运动,假设它的线速度的大小为v ,轨道半径近似等于地球半径R ,航天员受到的地球引力近似等于他在地面测得的体重mg 。
v2
R
FN =mg-m
FN <mg
当 时,座舱对航天员的支持力FN=0 ,航天员处于完全失重.
如果地球的引力突然消失,航天器将做什么样的运动呢?
离心运动
思考:为什么铁球与橡皮泥会飞出去?
定义:做圆周运动的物体,在其所受合外力突然消失,或不足以提供圆周运动所需向心力的情况下,就做逐渐远离圆心的运动,这种运动叫作离心运动。
做离心运动的条件:
离心运动
离心运动的应用
离心运动的防止
规律总结
F 合= 0 ,物体沿切线方向飞出远离圆心
F合<mω2r ,物体做逐渐远离圆心的运动
F合 = mω2r,物体做匀速圆周运动
F合>mω2r ,物体做逐渐靠近圆心的运动
巩固提升
在水平公路上行驶的汽车,当汽车以一定速度运动时,车轮与路面间的最大静摩擦力恰好等于汽车转弯所需要的向心力,汽车沿如图所示的圆形路径(虚线)运动,当汽车行驶速度突然增大,则汽车的运动路径可能是
A.Ⅰ B.Ⅱ C.Ⅲ D.Ⅳ
B
