数学(人教新课标B版)必修一 精品教学设计:2.4.2 求函数零点近似解的一种计算方法——二分法
文档属性
| 名称 | 数学(人教新课标B版)必修一 精品教学设计:2.4.2 求函数零点近似解的一种计算方法——二分法 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-28 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
示范教案
教学分析
求方程的解是常见的数学问题,这之前我们学 ( http: / / www.21cnjy.com )过解一元一次、一元二次方程,但有些方程求精确解较难.本节从另一个角度来求方程的近似解,这是一种崭新的思维方式,在现实生活中也有着广泛的应用.用二分法求方程近似解的特点是:运算量大,且重复相同的步骤,因此适合用计算器或计算机进行运算.在教学过程中要让学生体会到人类在方程求解中的不断进步.21教育名师原创作品
三维目标
1.让学生学会用二分法求方程的近似解,知道二分法是科学的数学方法.
2.了解用二分法求方程的近似解特点,学会用计算器或计算机求方程的近似解,初步了解算法思想.
3.回忆解方程的历史,了解人类解方程的进步历程,激发学习的热情和学习的兴趣.
重点难点
教学重点:用二分法求方程的近似解.
教学难点:二分法.
课时安排
1课时
导入新课
思路1.(情境导入)
师:(手拿一款手机)如果让你来猜这件商品的价格,你如何猜?
生1:先初步估算一个价格,如果高了再每隔10元降低报价.
生2:这样太慢了,先初步估算一个价格,如果 ( http: / / www.21cnjy.com )高了每隔100元降低报价.如果低了,每隔50元上升报价;如果再高了,每隔20元降低报价;如果低了,每隔10元上升报价……
生3:先初步估算一个价格,如果高了,再报一个价格;如果低了,就报两个价格和的一半;如果高了,再把报的低价与一半价相加再求其半,报出价格;如果低了,就把刚刚报出的价格与前面的价格结合起来取其和的半价……
师:在现实生活中我们也常常利用这种方法.譬 ( http: / / www.21cnjy.com )如,一天,我们华庄校区与锡南校区的线路出了故障(相距大约3 500米).电工是怎样检测的呢?是按照生1那样每隔10米或者按照生2那样每隔100米来检测,还是按照生3那样来检测呢?
生:(齐答)按照生3那样来检测.
师:生3的回答,我们可以用一个动态过程来展示一下(展示多媒体课件,区间逼近法).
思路2.(事例导入)
有12个小球,质量均匀,只有一个球是比别的球重,你用天平称几次可以找出这个球,要求次数越少越好.(让同学们自由发言,找出最好的办法)
解:第一次,两端各放六个球,低的那一端一定有重球.
第二次,两端各放三个球,低的那一端一定有重球.
第三次,两端各放一个球,如果平衡,剩下的就是重球,否则,低的就是重球.
其实这就是一种二分法的思想,那什么叫二分法呢?
推进新课
①解方程2x-16=0.
②解方程x2-x-2=0.21世纪教育网
③解方程x3-2x2-x+2=0.
④解方程 x2-2 x2-3x+2 =0.
⑤我们知道,函数f x =lnx+2x-6在区间 2,3 内有零点.进一步的问题是,如何找出这个零点的近似值?21cnjy.com
⑥“取中点”后,怎样判断所在零点的区间?
⑦什么叫二分法?
⑧试求函数f x =lnx+2x-6在区间 2,3 内零点的近似值.
⑨总结用二分法求函数零点近似值的步骤.,⑩思考用二分法求函数零点近似值的特点.
讨论结果:
①x=8.
②x=-1,x=2.
③x=-1,x=1,x=2
④x=-,x=,x=1,x=2.
⑤如果能够将零点所在的范围 ( http: / / www.21cnjy.com )尽量缩小,那么在一定精确度的要求下,我们可以得到零点的近似值.为了方便,我们通过“取中点”的方法逐步缩小零点所在的范围.〔“取中点”,一般地,我们把x=称为区间(a,b)的中点〕
⑥比如取区间(2,3)的中点2.5,用计算器算得f(2.5)<0,因为f(2.5)·f(3)<0,所以零点在区间(2.5,3)内.
⑦对于在区间[a,b]上连续不断且f( ( http: / / www.21cnjy.com )a)·f(b)<0的函数y=f(x),通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值.
像这样每次取区间的中点,将区间一分为二,再经比较,按需要留下其中一个小区间的方法称为二分法.
⑧因为函数f(x)=lnx+2x-6,用计算器或计算机作出函数f(x)=lnx+2x-6的对应值表.
x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.306 9 1.098 6 3.386 3 5.609 4 7.791 8 9.945 9 12.079 4 14.197 2
由表可知,f(2)<0,f(3)> ( http: / / www.21cnjy.com )0,则f(2)·f(3)<0,这说明f(x)在区间(2,3)内有零点x0,取区间(2,3)的中点x1=2.5,用计算器算得f(2.5)≈-0.084,因为f(2.5)·f(3)<0,所以x0∈(2.5,3).
同理,可得表(下表)与图象(如下图).
区间 中点的值 中点函数近似值
(2,3) 2.5 -0.084
(2.5,3) 2.75 0.512
(2.5,2.75) 2.625 0.215
(2.5,2.625) 2.562 5 0.066
(2.5,2.562 5) 2.531 25 -0.009
(2.531 25,2.562 5) 2.546 875 0.029
(2.531 25,2.546 875)[来源:21世纪教育网] 2.539 062 5 0.010
(2.531 25,2.539 062 5) 2.535 156 25 0.001
由于(2,3) (2.5,3) (2.5,2.75),所以零点所在的范围确实越来越小了.如果重复上述步骤,那么零点所在的范围会越来越小(见上表).这样,在一定的精确度下,我们可以在有限次重复相同步骤后,将所得的零点所在区间内的任意一点作为函数零点的近似值.特别地,可以将区间端点作为函数零点的近似值.例如,当精确度为0.01时,由于|2.539 062 5-2.531 25|=0.007 812 5<0.01,所以,我们可以将x=2.531 25作为函数f(x)=lnx+2x-6零点的近似值.21世纪教育网版权所有
⑨用二分法求函数零点的一般步骤如下:
第一步 在D内取一个闭区间[a0,b0] D,使f(a0)与f(b0)异号,即f(a0)·f(b0)<0.零点位于区间[a0,b0]中.21·cn·jy·com
第二步 取区间[a0,b0]的中点(如下图),则此中点对应的坐标为x0=a0+(b0-a0)=(a0+b0).【来源:21·世纪·教育·网】
计算f(x0)和f(a0),并判断:
(1)如果f(x0)=0,则x0就是f(x)的零点,计算终止;
(2)如果f(a0)·f(x0)<0,则零点位于区间[a0,x0]中,令a1=a0,b1=x0;
(3)如果f(a0)·f(x0)>0,则零点位于区间[x0,b0]中,令a1=x0,b1=b0.
第三步 取区间[a1,b1]的中点,则此中点对应的坐标为
x1=a1+(b1-a1)=(a1+b1).
计算f(x1)和f(a1),并判断:
(1)如果f(x1)=0,则x1就是f(x)的零点,计算终止;
(2)如果f(a1)·f(x1)<0,则零点位于区间[a1,x1]上,令a2=a1,b2=x1;
(3)如果f(a1)·f(x1)>0,则零点位于区间[x1,b1]上,令a2=x1,b2=b1.
……
继续实施上述步骤,直到区间[an, ( http: / / www.21cnjy.com )bn],函数的零点总位于区间[an,bn]上,当an和bn按照给定的精确度所取的近似值相同时,这个相同的近似值就是函数y=f(x)的近似零点,计算终止.这时函数y=f(x)的近似零点满足给定的精确度.21·世纪*教育网
⑩由函数的零点与相应方程的关系,我们可用二分 ( http: / / www.21cnjy.com )法来求方程的近似解.由于计算量较大,而且是重复相同的步骤,因此,我们可以通过设计一定的计算程序,借助计算器或计算机完成计算.21*cnjy*com
思路1
例1求函数f(x)=x3+x2-2x-2的一个正实数零点(精确到0.1).
解:由于f(1)=-2<0,f(2)=6>0,可以确定区间[1,2]作为计算的初始区间.用二法逐步计算,列表如下:
端点或中点横坐标 计算端点或中点的函数值 定区间
a0=1,b0=2 f(1)=-2,f(2)=6 [1,2]
x0=(1+2)/2=1.5 f(x0)=0.625>0 [1,1.5]
x1=(1+1.5)/2=1.25 f(x1)=-0.984<0 [1.25,1.5]
x2=(1.25+1.5)/2=1.375 f(x2)=-0.260<0 [1.375,1.5]
x3=(1.375+1.5)/2=1.437 5 f(x3)=0.162>0 [1.375,1.437 5]
由上表的计算可知,区间[1 ( http: / / www.21cnjy.com ).375,1.437 5]的左、右端点精确到0.1所取的近似值都是1.4,因此1.4就是所求函数的一个正实数零点的近似值.21教育网
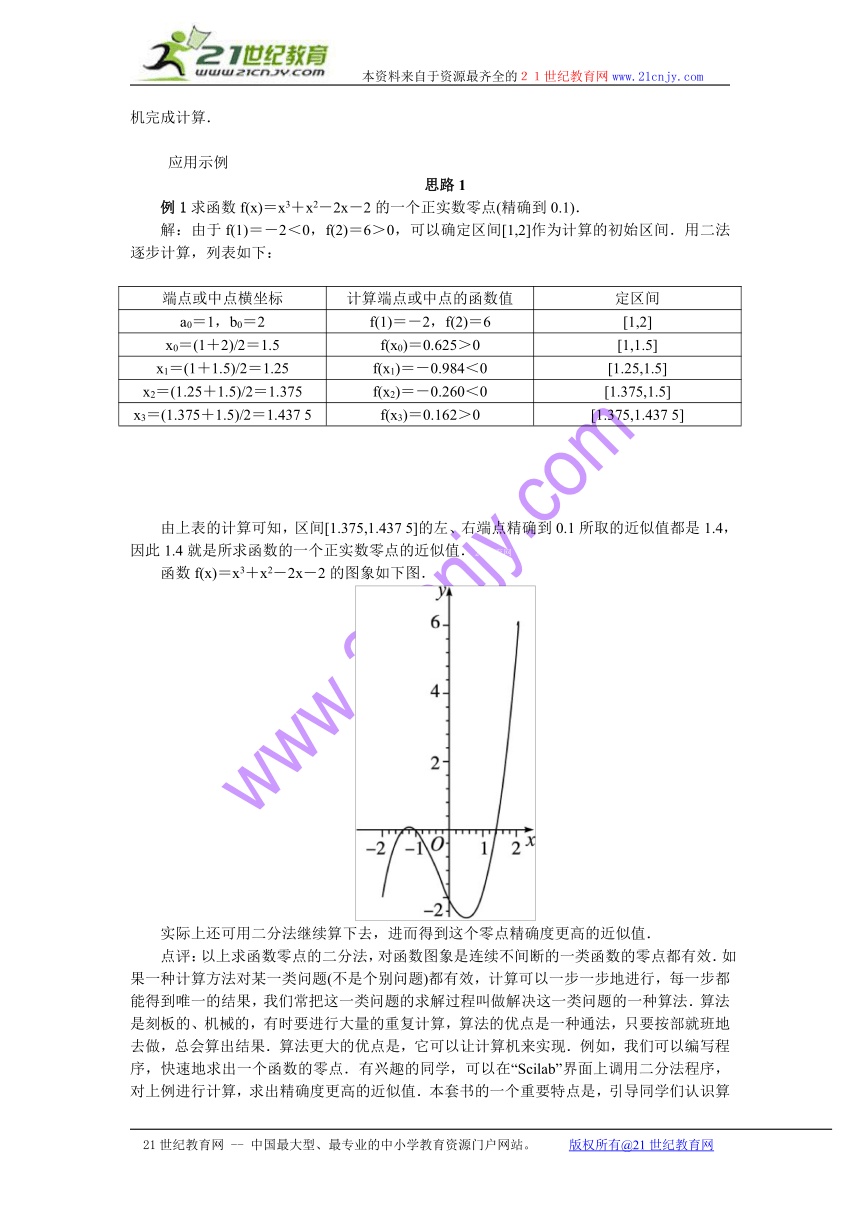
函数f(x)=x3+x2-2x-2的图象如下图.
实际上还可用二分法继续算下去,进而得到这个零点精确度更高的近似值.
点评:以上求函数零点的二分法,对函数图象是连续不间断的一类函数的零点都有效.如果一种计算方法对某一类问题(不是个别问题)都有效,计算可以一步一步地进行,每一步都能得到唯一的结果,我们常把这一类问题的求解过程叫做解决这一类问题的一种算法.算法是刻板的、机械的,有时要进行大量的重复计算,算法的优点是一种通法,只要按部就班地去做,总会算出结果.算法更大的优点是,它可以让计算机来实现.例如,我们可以编写程序,快速地求出一个函数的零点.有兴趣的同学,可以在“Scilab”界面上调用二分法程序,对上例进行计算,求出精确度更高的近似值.本套书的一个重要特点是,引导同学们认识算法思想的重要性,并希望同学们在学习前人算法的基础上,去寻求解决各类问题的算法.在数学3中,我们还要系统地学习算法.2·1·c·n·j·y
变式训练 若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法计算,其参考数据如下表:
f(1)=-2f(1.5)=0.625f(1.25)=-0.984f(1.375)=-0.260f(1.437 5)=0.162f(1.406 25)=-0.054
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为( )A.1.2 B.1.3 C.1.4 D.1.5解析:∵f(1.437 ( http: / / www.21cnjy.com )5)·f(1.406 25)<0,∴方程x3+x2-2x-2=0的一个正根位于区间(1.437 5,1.406 25)内,1.437 5与1.406 25精确到0.1的近似值都是1.4.答案:C
思路2
例1求方程2x3+3x-3=0的一个实数解(精确到0.01).
解:考察函数f(x)=2x3+3x-3,从一个两端函数值反号的区间开始,应用二分法逐步缩小方程实数解所在区间.2-1-c-n-j-y
经试算,f(0)=-3<0,f(2)= ( http: / / www.21cnjy.com )19>0,所以函数f(x)=2x3+3x-3在[0,2]内存在零点,即方程2x3+3x-3=0在[0,2]内有解.【来源:21cnj*y.co*m】
取[0,2]的中点1,经计算,f(1)=2>0,又f(0)<0,所以方程2x3+3x-3=0在[0,1]内有解.
如此下去,得到方程2x3+3x-3=0的实数解所在区间的表如下.
21世纪教育网
左端点 右端点
第1次 0 2
第2次 0 1
第3次 0.5 1
第4次 0.5 0.75
第5次 0.625 0.75
第6次 0.687 5 0.75
第7次 0.718 75 0.75
第8次 0.734 375 0.75
第9次 0.742 187 5 0.75
第10次 0.742 187 5 0.746 093 75
第11次 0.742 187 5 0.744 140 625
至此,可以看出,区间[0.742 18 ( http: / / www.21cnjy.com )7 5,0.744 140 625]内的所有值,若精确到0.01,都是0.74.所以0.74是方程2x3+3x-3=0精确到0.01的实数解.www.21-cn-jy.com
点评:利用二分法求方程近似解的步骤:
①确定函数f(x)的零点所在区间(a,b),通常令b-a=1;
②利用二分法求近似解.
变式训练利用计算器,求方程x2-2x-1=0的一个近似解(精确到0.1).活动:教师帮助学生分析:画出函数f(x)=x2-2x-1的图象,如图所示.从图象上可以发现,方程x2-2x-1=0的一个根x1在区间(2,3)内,另一个根x2在区间(-1,0)内.根据图象,我们发现f(2)=-1<0,f(3)=2>0,这表明此函数图象在区间(2,3)上穿过x轴一次,即方程f(x)=0在区间(2,3)上有唯一解.计算得f()=>0,发现x1∈(2,2.5)(如上图),这样可以进一步缩小x1所在的区间.解:设f(x)=x2-2x-1,先画出函数图象的简图,如上图.因为f(2)=-1<0,f(3)=2>0,所以在区间(2,3)内,方程x2-2x-1=0有一解,记为x1.取2与3的平均数2.5,因为f(2.5)=0.25>0,所以2<x1<2.5.再取2与2.5的平均数2.25,因为f(2.25)=-0.437 5<0,所以2.25<x1<2.5.如此继续下去,得f(2)<0,f(3)>0 x1∈(2,3),f(2)<0,f(2.5)>0 x1∈(2,2.5),f(2.25)<0,f(2.5)>0 x1∈(2.25,2.5),f(2.375)<0,f(2.5)>0 x1∈(2.375,2.5),f(2.375)<0,f(2.437 5)>0 x1∈(2.375,2.437 5).因为2.375与2.437 5精确到0.1的近似值都为2.4,所以此方程的一个近似解为2.4.点评:利用同样的方法,还可以求出方程的另一个近似解.
1.函数f(x)=x3-2x2-x+2的零点个数是( )
A.0 B.1 C.2 D.3
答案:D
2.在26枚崭新的金币中,有一枚外表与真币完全相同的假币(重量轻一点),现在只有一台天平,请问:应用二分法的思想,最多称__________次就可以发现这枚假币?
解析:将26枚金币平均分成两份,放在天平上,则假币在轻的那13枚金币里面;将这13枚金币拿出1枚,将剩下的12枚平均分成两份,放在天平上,若天平平衡,则假币一定是拿出的那一枚,若不平衡,则假币一定在轻的那6枚金币里面;将这6枚平均分成两份,放在天平上,则假币一定在轻的那3枚金币里面;将这3枚金币任拿出2枚放在天平上,若平衡,则剩下的那一枚就是假币,若不平衡,则轻的那一枚就是假币.综上可知,最多称4次就可以发现这枚假币.www-2-1-cnjy-com
答案:4
3.求方程x3-3x-1=0的一个正的近似解(精确到0.1).
解:设f(x)=x3-3x-1,设x1为函数的零点,即方程x3-3x-1=0的解.
作出函数f(x)=x3-3x-1的图象如下图.
因为f(1)=-3<0,f(2)=1>0,所以在区间(1,2)内方程x3-3x-1=0有一个解,记为x1.取1与2的平均数1. 5,因为f(1.5)=-2.125<0,所以1.5<x1<2.
再取2与1.5的平均数1.75,
因为f(1.75)=-0.890 625<0,所以1.75<x1<2.
如此继续下去,得21世纪教育网
f(1)<0,f(2)>0 x1∈(1,2),
f(1.5)<0,f(2)>0 x1∈(1.5,2),
f(1.75)<0,f(2)>0 x1∈(1.75,2),
f(1.875)<0,f(2)>0 x1∈(1.875,2),
f(1.875)<0,f(1.937 5)>0 x1∈(1.875,1.937 5),
因为区间[1.875,1.937 5]内的所有值,如精确到0.1都是1.9,
所以1.9是方程x3-3x-1的实数解.
从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查接点的个数为多少? 21*cnjy*com
(此例既体现了二分法的应用价值,也有利于发展学生的应用意识)
答案:至少需要检查接点的个数为4.
①掌握用二分法求方程的近似解,及二分法的其他应用.
②思想方法:函数方程思想、数形结合思想.
课本习题2—4 A 7.
“猜价格”的游戏深受人们的喜欢,它 ( http: / / www.21cnjy.com )是二分法的具体应用,用它引入拉近了数学与生活的距离.二分法是科学的数学方法,它在求方程的近似解和现实生活中都有着广泛的应用.本节设计紧紧围绕这两个中心展开,充分借助现代教学手段,用多种角度处理问题,使学生充分体会数学思想方法的科学性与完美性.【出处:21教育名师】
基本初等函数的零点个数
结合基本初等函数的图象得:
①正比例函数y=kx(k≠0)仅有一个零点0;
②反比例函数y=(k≠0)没有零点;
③一次函数y=kx+b(k≠0)仅有一个零点;
④二次函数y=ax2+bx+c(a≠0) ( http: / / www.21cnjy.com ),当Δ>0时,二次函数有两个零点;当Δ=0时,二次函数仅有一个零点;当Δ<0时,二次函数无零点.【版权所有:21教育】
(设计者:张新军)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
示范教案
教学分析
求方程的解是常见的数学问题,这之前我们学 ( http: / / www.21cnjy.com )过解一元一次、一元二次方程,但有些方程求精确解较难.本节从另一个角度来求方程的近似解,这是一种崭新的思维方式,在现实生活中也有着广泛的应用.用二分法求方程近似解的特点是:运算量大,且重复相同的步骤,因此适合用计算器或计算机进行运算.在教学过程中要让学生体会到人类在方程求解中的不断进步.21教育名师原创作品
三维目标
1.让学生学会用二分法求方程的近似解,知道二分法是科学的数学方法.
2.了解用二分法求方程的近似解特点,学会用计算器或计算机求方程的近似解,初步了解算法思想.
3.回忆解方程的历史,了解人类解方程的进步历程,激发学习的热情和学习的兴趣.
重点难点
教学重点:用二分法求方程的近似解.
教学难点:二分法.
课时安排
1课时
导入新课
思路1.(情境导入)
师:(手拿一款手机)如果让你来猜这件商品的价格,你如何猜?
生1:先初步估算一个价格,如果高了再每隔10元降低报价.
生2:这样太慢了,先初步估算一个价格,如果 ( http: / / www.21cnjy.com )高了每隔100元降低报价.如果低了,每隔50元上升报价;如果再高了,每隔20元降低报价;如果低了,每隔10元上升报价……
生3:先初步估算一个价格,如果高了,再报一个价格;如果低了,就报两个价格和的一半;如果高了,再把报的低价与一半价相加再求其半,报出价格;如果低了,就把刚刚报出的价格与前面的价格结合起来取其和的半价……
师:在现实生活中我们也常常利用这种方法.譬 ( http: / / www.21cnjy.com )如,一天,我们华庄校区与锡南校区的线路出了故障(相距大约3 500米).电工是怎样检测的呢?是按照生1那样每隔10米或者按照生2那样每隔100米来检测,还是按照生3那样来检测呢?
生:(齐答)按照生3那样来检测.
师:生3的回答,我们可以用一个动态过程来展示一下(展示多媒体课件,区间逼近法).
思路2.(事例导入)
有12个小球,质量均匀,只有一个球是比别的球重,你用天平称几次可以找出这个球,要求次数越少越好.(让同学们自由发言,找出最好的办法)
解:第一次,两端各放六个球,低的那一端一定有重球.
第二次,两端各放三个球,低的那一端一定有重球.
第三次,两端各放一个球,如果平衡,剩下的就是重球,否则,低的就是重球.
其实这就是一种二分法的思想,那什么叫二分法呢?
推进新课
①解方程2x-16=0.
②解方程x2-x-2=0.21世纪教育网
③解方程x3-2x2-x+2=0.
④解方程 x2-2 x2-3x+2 =0.
⑤我们知道,函数f x =lnx+2x-6在区间 2,3 内有零点.进一步的问题是,如何找出这个零点的近似值?21cnjy.com
⑥“取中点”后,怎样判断所在零点的区间?
⑦什么叫二分法?
⑧试求函数f x =lnx+2x-6在区间 2,3 内零点的近似值.
⑨总结用二分法求函数零点近似值的步骤.,⑩思考用二分法求函数零点近似值的特点.
讨论结果:
①x=8.
②x=-1,x=2.
③x=-1,x=1,x=2
④x=-,x=,x=1,x=2.
⑤如果能够将零点所在的范围 ( http: / / www.21cnjy.com )尽量缩小,那么在一定精确度的要求下,我们可以得到零点的近似值.为了方便,我们通过“取中点”的方法逐步缩小零点所在的范围.〔“取中点”,一般地,我们把x=称为区间(a,b)的中点〕
⑥比如取区间(2,3)的中点2.5,用计算器算得f(2.5)<0,因为f(2.5)·f(3)<0,所以零点在区间(2.5,3)内.
⑦对于在区间[a,b]上连续不断且f( ( http: / / www.21cnjy.com )a)·f(b)<0的函数y=f(x),通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值.
像这样每次取区间的中点,将区间一分为二,再经比较,按需要留下其中一个小区间的方法称为二分法.
⑧因为函数f(x)=lnx+2x-6,用计算器或计算机作出函数f(x)=lnx+2x-6的对应值表.
x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.306 9 1.098 6 3.386 3 5.609 4 7.791 8 9.945 9 12.079 4 14.197 2
由表可知,f(2)<0,f(3)> ( http: / / www.21cnjy.com )0,则f(2)·f(3)<0,这说明f(x)在区间(2,3)内有零点x0,取区间(2,3)的中点x1=2.5,用计算器算得f(2.5)≈-0.084,因为f(2.5)·f(3)<0,所以x0∈(2.5,3).
同理,可得表(下表)与图象(如下图).
区间 中点的值 中点函数近似值
(2,3) 2.5 -0.084
(2.5,3) 2.75 0.512
(2.5,2.75) 2.625 0.215
(2.5,2.625) 2.562 5 0.066
(2.5,2.562 5) 2.531 25 -0.009
(2.531 25,2.562 5) 2.546 875 0.029
(2.531 25,2.546 875)[来源:21世纪教育网] 2.539 062 5 0.010
(2.531 25,2.539 062 5) 2.535 156 25 0.001
由于(2,3) (2.5,3) (2.5,2.75),所以零点所在的范围确实越来越小了.如果重复上述步骤,那么零点所在的范围会越来越小(见上表).这样,在一定的精确度下,我们可以在有限次重复相同步骤后,将所得的零点所在区间内的任意一点作为函数零点的近似值.特别地,可以将区间端点作为函数零点的近似值.例如,当精确度为0.01时,由于|2.539 062 5-2.531 25|=0.007 812 5<0.01,所以,我们可以将x=2.531 25作为函数f(x)=lnx+2x-6零点的近似值.21世纪教育网版权所有
⑨用二分法求函数零点的一般步骤如下:
第一步 在D内取一个闭区间[a0,b0] D,使f(a0)与f(b0)异号,即f(a0)·f(b0)<0.零点位于区间[a0,b0]中.21·cn·jy·com
第二步 取区间[a0,b0]的中点(如下图),则此中点对应的坐标为x0=a0+(b0-a0)=(a0+b0).【来源:21·世纪·教育·网】
计算f(x0)和f(a0),并判断:
(1)如果f(x0)=0,则x0就是f(x)的零点,计算终止;
(2)如果f(a0)·f(x0)<0,则零点位于区间[a0,x0]中,令a1=a0,b1=x0;
(3)如果f(a0)·f(x0)>0,则零点位于区间[x0,b0]中,令a1=x0,b1=b0.
第三步 取区间[a1,b1]的中点,则此中点对应的坐标为
x1=a1+(b1-a1)=(a1+b1).
计算f(x1)和f(a1),并判断:
(1)如果f(x1)=0,则x1就是f(x)的零点,计算终止;
(2)如果f(a1)·f(x1)<0,则零点位于区间[a1,x1]上,令a2=a1,b2=x1;
(3)如果f(a1)·f(x1)>0,则零点位于区间[x1,b1]上,令a2=x1,b2=b1.
……
继续实施上述步骤,直到区间[an, ( http: / / www.21cnjy.com )bn],函数的零点总位于区间[an,bn]上,当an和bn按照给定的精确度所取的近似值相同时,这个相同的近似值就是函数y=f(x)的近似零点,计算终止.这时函数y=f(x)的近似零点满足给定的精确度.21·世纪*教育网
⑩由函数的零点与相应方程的关系,我们可用二分 ( http: / / www.21cnjy.com )法来求方程的近似解.由于计算量较大,而且是重复相同的步骤,因此,我们可以通过设计一定的计算程序,借助计算器或计算机完成计算.21*cnjy*com
思路1
例1求函数f(x)=x3+x2-2x-2的一个正实数零点(精确到0.1).
解:由于f(1)=-2<0,f(2)=6>0,可以确定区间[1,2]作为计算的初始区间.用二法逐步计算,列表如下:
端点或中点横坐标 计算端点或中点的函数值 定区间
a0=1,b0=2 f(1)=-2,f(2)=6 [1,2]
x0=(1+2)/2=1.5 f(x0)=0.625>0 [1,1.5]
x1=(1+1.5)/2=1.25 f(x1)=-0.984<0 [1.25,1.5]
x2=(1.25+1.5)/2=1.375 f(x2)=-0.260<0 [1.375,1.5]
x3=(1.375+1.5)/2=1.437 5 f(x3)=0.162>0 [1.375,1.437 5]
由上表的计算可知,区间[1 ( http: / / www.21cnjy.com ).375,1.437 5]的左、右端点精确到0.1所取的近似值都是1.4,因此1.4就是所求函数的一个正实数零点的近似值.21教育网
函数f(x)=x3+x2-2x-2的图象如下图.
实际上还可用二分法继续算下去,进而得到这个零点精确度更高的近似值.
点评:以上求函数零点的二分法,对函数图象是连续不间断的一类函数的零点都有效.如果一种计算方法对某一类问题(不是个别问题)都有效,计算可以一步一步地进行,每一步都能得到唯一的结果,我们常把这一类问题的求解过程叫做解决这一类问题的一种算法.算法是刻板的、机械的,有时要进行大量的重复计算,算法的优点是一种通法,只要按部就班地去做,总会算出结果.算法更大的优点是,它可以让计算机来实现.例如,我们可以编写程序,快速地求出一个函数的零点.有兴趣的同学,可以在“Scilab”界面上调用二分法程序,对上例进行计算,求出精确度更高的近似值.本套书的一个重要特点是,引导同学们认识算法思想的重要性,并希望同学们在学习前人算法的基础上,去寻求解决各类问题的算法.在数学3中,我们还要系统地学习算法.2·1·c·n·j·y
变式训练 若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法计算,其参考数据如下表:
f(1)=-2f(1.5)=0.625f(1.25)=-0.984f(1.375)=-0.260f(1.437 5)=0.162f(1.406 25)=-0.054
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为( )A.1.2 B.1.3 C.1.4 D.1.5解析:∵f(1.437 ( http: / / www.21cnjy.com )5)·f(1.406 25)<0,∴方程x3+x2-2x-2=0的一个正根位于区间(1.437 5,1.406 25)内,1.437 5与1.406 25精确到0.1的近似值都是1.4.答案:C
思路2
例1求方程2x3+3x-3=0的一个实数解(精确到0.01).
解:考察函数f(x)=2x3+3x-3,从一个两端函数值反号的区间开始,应用二分法逐步缩小方程实数解所在区间.2-1-c-n-j-y
经试算,f(0)=-3<0,f(2)= ( http: / / www.21cnjy.com )19>0,所以函数f(x)=2x3+3x-3在[0,2]内存在零点,即方程2x3+3x-3=0在[0,2]内有解.【来源:21cnj*y.co*m】
取[0,2]的中点1,经计算,f(1)=2>0,又f(0)<0,所以方程2x3+3x-3=0在[0,1]内有解.
如此下去,得到方程2x3+3x-3=0的实数解所在区间的表如下.
21世纪教育网
左端点 右端点
第1次 0 2
第2次 0 1
第3次 0.5 1
第4次 0.5 0.75
第5次 0.625 0.75
第6次 0.687 5 0.75
第7次 0.718 75 0.75
第8次 0.734 375 0.75
第9次 0.742 187 5 0.75
第10次 0.742 187 5 0.746 093 75
第11次 0.742 187 5 0.744 140 625
至此,可以看出,区间[0.742 18 ( http: / / www.21cnjy.com )7 5,0.744 140 625]内的所有值,若精确到0.01,都是0.74.所以0.74是方程2x3+3x-3=0精确到0.01的实数解.www.21-cn-jy.com
点评:利用二分法求方程近似解的步骤:
①确定函数f(x)的零点所在区间(a,b),通常令b-a=1;
②利用二分法求近似解.
变式训练利用计算器,求方程x2-2x-1=0的一个近似解(精确到0.1).活动:教师帮助学生分析:画出函数f(x)=x2-2x-1的图象,如图所示.从图象上可以发现,方程x2-2x-1=0的一个根x1在区间(2,3)内,另一个根x2在区间(-1,0)内.根据图象,我们发现f(2)=-1<0,f(3)=2>0,这表明此函数图象在区间(2,3)上穿过x轴一次,即方程f(x)=0在区间(2,3)上有唯一解.计算得f()=>0,发现x1∈(2,2.5)(如上图),这样可以进一步缩小x1所在的区间.解:设f(x)=x2-2x-1,先画出函数图象的简图,如上图.因为f(2)=-1<0,f(3)=2>0,所以在区间(2,3)内,方程x2-2x-1=0有一解,记为x1.取2与3的平均数2.5,因为f(2.5)=0.25>0,所以2<x1<2.5.再取2与2.5的平均数2.25,因为f(2.25)=-0.437 5<0,所以2.25<x1<2.5.如此继续下去,得f(2)<0,f(3)>0 x1∈(2,3),f(2)<0,f(2.5)>0 x1∈(2,2.5),f(2.25)<0,f(2.5)>0 x1∈(2.25,2.5),f(2.375)<0,f(2.5)>0 x1∈(2.375,2.5),f(2.375)<0,f(2.437 5)>0 x1∈(2.375,2.437 5).因为2.375与2.437 5精确到0.1的近似值都为2.4,所以此方程的一个近似解为2.4.点评:利用同样的方法,还可以求出方程的另一个近似解.
1.函数f(x)=x3-2x2-x+2的零点个数是( )
A.0 B.1 C.2 D.3
答案:D
2.在26枚崭新的金币中,有一枚外表与真币完全相同的假币(重量轻一点),现在只有一台天平,请问:应用二分法的思想,最多称__________次就可以发现这枚假币?
解析:将26枚金币平均分成两份,放在天平上,则假币在轻的那13枚金币里面;将这13枚金币拿出1枚,将剩下的12枚平均分成两份,放在天平上,若天平平衡,则假币一定是拿出的那一枚,若不平衡,则假币一定在轻的那6枚金币里面;将这6枚平均分成两份,放在天平上,则假币一定在轻的那3枚金币里面;将这3枚金币任拿出2枚放在天平上,若平衡,则剩下的那一枚就是假币,若不平衡,则轻的那一枚就是假币.综上可知,最多称4次就可以发现这枚假币.www-2-1-cnjy-com
答案:4
3.求方程x3-3x-1=0的一个正的近似解(精确到0.1).
解:设f(x)=x3-3x-1,设x1为函数的零点,即方程x3-3x-1=0的解.
作出函数f(x)=x3-3x-1的图象如下图.
因为f(1)=-3<0,f(2)=1>0,所以在区间(1,2)内方程x3-3x-1=0有一个解,记为x1.取1与2的平均数1. 5,因为f(1.5)=-2.125<0,所以1.5<x1<2.
再取2与1.5的平均数1.75,
因为f(1.75)=-0.890 625<0,所以1.75<x1<2.
如此继续下去,得21世纪教育网
f(1)<0,f(2)>0 x1∈(1,2),
f(1.5)<0,f(2)>0 x1∈(1.5,2),
f(1.75)<0,f(2)>0 x1∈(1.75,2),
f(1.875)<0,f(2)>0 x1∈(1.875,2),
f(1.875)<0,f(1.937 5)>0 x1∈(1.875,1.937 5),
因为区间[1.875,1.937 5]内的所有值,如精确到0.1都是1.9,
所以1.9是方程x3-3x-1的实数解.
从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查接点的个数为多少? 21*cnjy*com
(此例既体现了二分法的应用价值,也有利于发展学生的应用意识)
答案:至少需要检查接点的个数为4.
①掌握用二分法求方程的近似解,及二分法的其他应用.
②思想方法:函数方程思想、数形结合思想.
课本习题2—4 A 7.
“猜价格”的游戏深受人们的喜欢,它 ( http: / / www.21cnjy.com )是二分法的具体应用,用它引入拉近了数学与生活的距离.二分法是科学的数学方法,它在求方程的近似解和现实生活中都有着广泛的应用.本节设计紧紧围绕这两个中心展开,充分借助现代教学手段,用多种角度处理问题,使学生充分体会数学思想方法的科学性与完美性.【出处:21教育名师】
基本初等函数的零点个数
结合基本初等函数的图象得:
①正比例函数y=kx(k≠0)仅有一个零点0;
②反比例函数y=(k≠0)没有零点;
③一次函数y=kx+b(k≠0)仅有一个零点;
④二次函数y=ax2+bx+c(a≠0) ( http: / / www.21cnjy.com ),当Δ>0时,二次函数有两个零点;当Δ=0时,二次函数仅有一个零点;当Δ<0时,二次函数无零点.【版权所有:21教育】
(设计者:张新军)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
