人教版高中物理必修第二册 7.2 万有引力定律 课件(共46张PPT)
文档属性
| 名称 | 人教版高中物理必修第二册 7.2 万有引力定律 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-07 12:54:17 | ||
图片预览





文档简介
(共46张PPT)
第七章
万有引力与宇宙航行
2.万有引力定律
知识回顾: 开普勒三定律
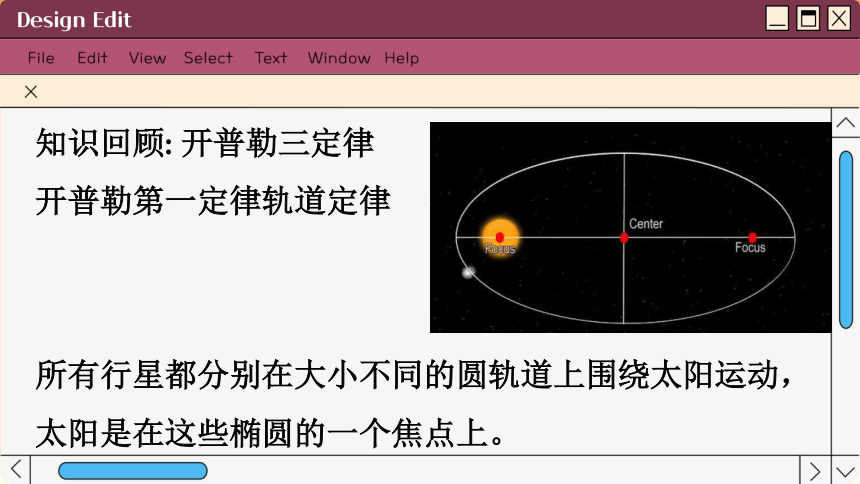
开普勒第一定律轨道定律
所有行星都分别在大小不同的圆轨道上围绕太阳运动,太阳是在这些椭圆的一个焦点上。
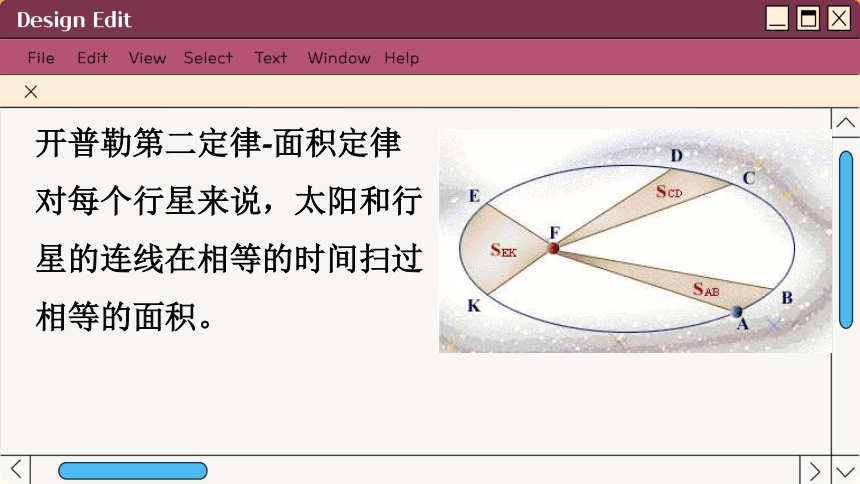
开普勒第二定律-面积定律
对每个行星来说,太阳和行星的连线在相等的时间扫过相等的面积。
开普勒第三定律-周期定律
所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
问题探究:
行星为什么绕太阳如此和谐而又有规律地做椭圆运动
一切物体都有合并的趋势。
行星的运动是受到了来自太阳的类似于磁力的作用 ,与距离成反比。
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动
行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
牛顿(1643-1727)英国著名的物理学家
当年牛顿在前人研究的基础上,并凭借其超凡的数学能力和坚定的信念,深入研究,最终发现了万有引力定律。
行星与太阳间的引力
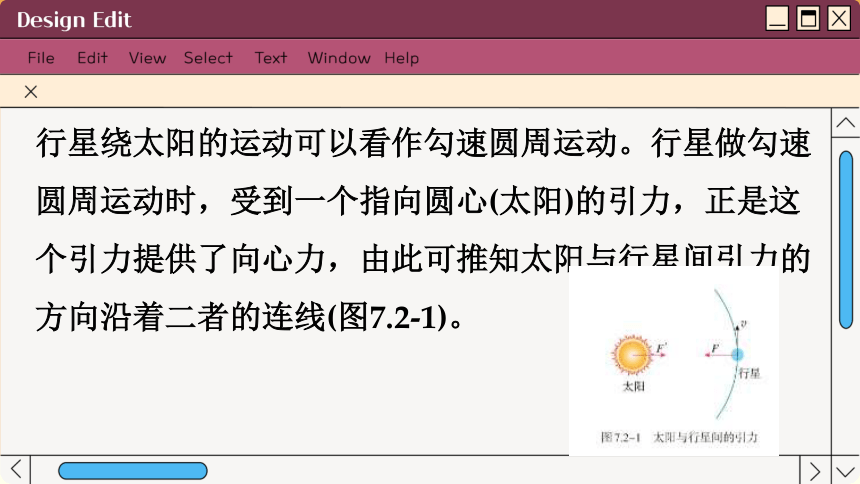
行星绕太阳的运动可以看作勾速圆周运动。行星做勾速圆周运动时,受到一个指向圆心(太阳)的引力,正是这个引力提供了向心力,由此可推知太阳与行星间引力的方向沿着二者的连线(图7.2-1)。
建立模型:
行星的实际运动是椭圆运动,但我们还不了解圆运动规律,那应该怎么办 能把它简化成什么运动呢
既然把行星绕太阳的运动简化为圆周运动。那么行星绕太阳运动可看成匀速圆周运动还是变速圆周运动
行星绕太阳做匀速圆周运动需要向心力,那什么力来提供做向心力 这个力的方向怎么样
太阳对行星的引力提供向心力,那这个力大小有什么样的定量关系呢
行星运行速度v不容易观测 怎么办
消去v
太阳对行星的引力:
结论:太阳对行星的引力跟受力星体的质量成正比,与行星、太阳距离的二次方成反比。
关系式中m是受力天体还是施力天体的质量
月一地检验
地球绕太阳运动,月球绕地球运动,它们之间的作用力是同一种性质的力吗 这种力与地球对树上苹果的吸引力也是同一种性质的力吗(图7.2-2)
思考与讨论
已知自由落体加速度g为9.8 m/s”,月球中心与地球中心的距离为3.8x l0m,月球公转周期为27.3 d,约2.36x 10s。根据这些效据,能否验证前面的假设
在牛顿的时代,人们已经能够比较精确地测定自由落体加速度,当时也能比较精确地测定月球与地球的距离月球公转的周期,从而能够算出月球运动的向心加速度计算结果与预期符合得很好。这表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力.真的遵从相同的规律!
万有引力定律
1、内容: 自然界中任何两个物体都相互吸引引力的方向在它们的连线上,引力的大小跟这两个物体的质量m1和m2的乘积成正比,跟它们的距离r的二次方成反比。
万有引力定律
2、公式
公式的适用条件:
1.万有引力存在于一切物体之间,但万有引力公式适用于质点间的引力大小的计算。
r为质点间的距离,两物体的形状和大小对其间距的影响可忽略不计,r>R。
2.两质量分布均匀的球体之间的引力,也可用上述公式计算,且r为两球心间距离。
3.一个质量分布均匀的球体与球外一个质点间的万有引力,r为球心到质点间的距离。
万有引力的性质
1.普遍性万有引力存在于任何两个有质量的物体之间,它是自然果中物质间基本的相互作用之一
2.宏观性一般物体之间虽然存在万有引力,但是很小,只有天体与物体之间或天体之间万有引力才比较显著,因此,涉及天体运动时,才考虑万有引力。
3.相互性
万有引力的作用是相互的,符合牛顿第三定律
4.独立性
两物体间的万有引力只与它们本身的质量和它们间的距离有关,与周围有无其他物质无关
引力常量
牛顿得出了万有引力与物体质量及它们之间距离的关系,但却无法算出两个天体之间万有引力的大小,因为他不知道引力常量 G的值
一百多年以后,英国物理学家卡文迪什通过实验测量了几个铅球之间的引力。由这一实验结果可推算出引力常量G的值。国际科技数据委员会2014年的推荐值G=6.674 08(31)×10-11N·m2/kg2,通常取 G=6.67 ×10-11N·m2/kg2
思考与讨论
一个篮球的质量为0.6 kg,它所受的重力有多大 试估算操场上相距0.5 m的两个篮球之间的万有引力。
引力常量是自然界中少数几个最重要的物理常量之一。在对一些物体间的引力进行测量并算出引力常量 G以后人们又测量了多种物体间的引力,所得结果与利用引力常量G按万有引力定律计算所得的结果相同。引力常量的普适性成了万有引力定律正确性的有力证据。
引力恒量的测定:
装置介绍:T形架、石英丝、镜尺、M球和m球
(2)测量原理介绍:扭秤达到平衡时,引力矩等于石英丝的阻力矩。石英丝转角可由镜尺测出,由石英丝转角可知扭力矩等于引力矩,从而可测得万有引力,进而可测引力恒量G.
科学漫步
牛顿的科学生涯
牛顿 一- 伟大的科学家,牛顿力学理论体系的建立者,1643年1月4日"涎生在英格兰的林肯郡。牛顿于1661年造入剑桥大学三一学院,1665年获得学士学位
1665~1666年伦敦鼠疫流行,学校停课,牛顿回到故乡。牛顿在剑桥受到数学和自然科学的培养和熏陶,对探索自然现象产生了极浓厚的兴趣,就在躲避鼠疫这两年内,他在自然科学领城思潮奔腾,思考了前人从未想过的问题,创建了惊人的业绩。
1665年初,牛顿创立了级数近似法和把任何幂的二项式化为一个级教的方法,同年11月创立了微分学。次年1月,牛顿研究颜色理论,5月开始研究积分学。这一年内,牛顿还开始研究重力问题,并把重力与月球的运动、行星的运动联系起来考虑。
他从开普勒行星运动定律出发通过数学淮导发现:使行星保持在它们轨道上的力,必定与行星到转动中心的距离的二次方成反比。由此可见,牛预一生中最重大的科学思想,是在他二十多岁时思想敏锐的短短两年期间孕育、萌发和形成的。
1.地球的半径为R某卫星在地球表面附近所受万有引力为F,则该卫星在离地面高度约6R的轨道上受到的万有引力约为( )
6F B.7F
C. F D. F
2.已知在太阳系外某“宜居”行星的质量约为地球质量的6.4倍一个在地球表面重力为600 N的人在这个行星表面的重力将变为960 N。由此可推知,该行星的半径与地球半径之比约为( )
A.1 : 2 B.2 : 1 C.3 : 2 D.4 : 1
3.载人火箭竖直升空的加速度为a=50 m/s2某时刻运载舱中质量m=60 kg的航天员对座椅的压力测量值为3 060 N,已知地球表面的重力加速度为10 m/s2,3.16,设地球半径为R,以下判断正确的有( )
A.此时火箭距地面的高度约为3R
B.此时火箭内的航天员处于完全失重状态
C.此时航天员所处位置的重力加速度为1 m/s2
D.此时航天员受到地球的引力为3 060 N
第七章
万有引力与宇宙航行
2.万有引力定律
知识回顾: 开普勒三定律
开普勒第一定律轨道定律
所有行星都分别在大小不同的圆轨道上围绕太阳运动,太阳是在这些椭圆的一个焦点上。
开普勒第二定律-面积定律
对每个行星来说,太阳和行星的连线在相等的时间扫过相等的面积。
开普勒第三定律-周期定律
所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
问题探究:
行星为什么绕太阳如此和谐而又有规律地做椭圆运动
一切物体都有合并的趋势。
行星的运动是受到了来自太阳的类似于磁力的作用 ,与距离成反比。
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动
行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
牛顿(1643-1727)英国著名的物理学家
当年牛顿在前人研究的基础上,并凭借其超凡的数学能力和坚定的信念,深入研究,最终发现了万有引力定律。
行星与太阳间的引力
行星绕太阳的运动可以看作勾速圆周运动。行星做勾速圆周运动时,受到一个指向圆心(太阳)的引力,正是这个引力提供了向心力,由此可推知太阳与行星间引力的方向沿着二者的连线(图7.2-1)。
建立模型:
行星的实际运动是椭圆运动,但我们还不了解圆运动规律,那应该怎么办 能把它简化成什么运动呢
既然把行星绕太阳的运动简化为圆周运动。那么行星绕太阳运动可看成匀速圆周运动还是变速圆周运动
行星绕太阳做匀速圆周运动需要向心力,那什么力来提供做向心力 这个力的方向怎么样
太阳对行星的引力提供向心力,那这个力大小有什么样的定量关系呢
行星运行速度v不容易观测 怎么办
消去v
太阳对行星的引力:
结论:太阳对行星的引力跟受力星体的质量成正比,与行星、太阳距离的二次方成反比。
关系式中m是受力天体还是施力天体的质量
月一地检验
地球绕太阳运动,月球绕地球运动,它们之间的作用力是同一种性质的力吗 这种力与地球对树上苹果的吸引力也是同一种性质的力吗(图7.2-2)
思考与讨论
已知自由落体加速度g为9.8 m/s”,月球中心与地球中心的距离为3.8x l0m,月球公转周期为27.3 d,约2.36x 10s。根据这些效据,能否验证前面的假设
在牛顿的时代,人们已经能够比较精确地测定自由落体加速度,当时也能比较精确地测定月球与地球的距离月球公转的周期,从而能够算出月球运动的向心加速度计算结果与预期符合得很好。这表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力.真的遵从相同的规律!
万有引力定律
1、内容: 自然界中任何两个物体都相互吸引引力的方向在它们的连线上,引力的大小跟这两个物体的质量m1和m2的乘积成正比,跟它们的距离r的二次方成反比。
万有引力定律
2、公式
公式的适用条件:
1.万有引力存在于一切物体之间,但万有引力公式适用于质点间的引力大小的计算。
r为质点间的距离,两物体的形状和大小对其间距的影响可忽略不计,r>R。
2.两质量分布均匀的球体之间的引力,也可用上述公式计算,且r为两球心间距离。
3.一个质量分布均匀的球体与球外一个质点间的万有引力,r为球心到质点间的距离。
万有引力的性质
1.普遍性万有引力存在于任何两个有质量的物体之间,它是自然果中物质间基本的相互作用之一
2.宏观性一般物体之间虽然存在万有引力,但是很小,只有天体与物体之间或天体之间万有引力才比较显著,因此,涉及天体运动时,才考虑万有引力。
3.相互性
万有引力的作用是相互的,符合牛顿第三定律
4.独立性
两物体间的万有引力只与它们本身的质量和它们间的距离有关,与周围有无其他物质无关
引力常量
牛顿得出了万有引力与物体质量及它们之间距离的关系,但却无法算出两个天体之间万有引力的大小,因为他不知道引力常量 G的值
一百多年以后,英国物理学家卡文迪什通过实验测量了几个铅球之间的引力。由这一实验结果可推算出引力常量G的值。国际科技数据委员会2014年的推荐值G=6.674 08(31)×10-11N·m2/kg2,通常取 G=6.67 ×10-11N·m2/kg2
思考与讨论
一个篮球的质量为0.6 kg,它所受的重力有多大 试估算操场上相距0.5 m的两个篮球之间的万有引力。
引力常量是自然界中少数几个最重要的物理常量之一。在对一些物体间的引力进行测量并算出引力常量 G以后人们又测量了多种物体间的引力,所得结果与利用引力常量G按万有引力定律计算所得的结果相同。引力常量的普适性成了万有引力定律正确性的有力证据。
引力恒量的测定:
装置介绍:T形架、石英丝、镜尺、M球和m球
(2)测量原理介绍:扭秤达到平衡时,引力矩等于石英丝的阻力矩。石英丝转角可由镜尺测出,由石英丝转角可知扭力矩等于引力矩,从而可测得万有引力,进而可测引力恒量G.
科学漫步
牛顿的科学生涯
牛顿 一- 伟大的科学家,牛顿力学理论体系的建立者,1643年1月4日"涎生在英格兰的林肯郡。牛顿于1661年造入剑桥大学三一学院,1665年获得学士学位
1665~1666年伦敦鼠疫流行,学校停课,牛顿回到故乡。牛顿在剑桥受到数学和自然科学的培养和熏陶,对探索自然现象产生了极浓厚的兴趣,就在躲避鼠疫这两年内,他在自然科学领城思潮奔腾,思考了前人从未想过的问题,创建了惊人的业绩。
1665年初,牛顿创立了级数近似法和把任何幂的二项式化为一个级教的方法,同年11月创立了微分学。次年1月,牛顿研究颜色理论,5月开始研究积分学。这一年内,牛顿还开始研究重力问题,并把重力与月球的运动、行星的运动联系起来考虑。
他从开普勒行星运动定律出发通过数学淮导发现:使行星保持在它们轨道上的力,必定与行星到转动中心的距离的二次方成反比。由此可见,牛预一生中最重大的科学思想,是在他二十多岁时思想敏锐的短短两年期间孕育、萌发和形成的。
1.地球的半径为R某卫星在地球表面附近所受万有引力为F,则该卫星在离地面高度约6R的轨道上受到的万有引力约为( )
6F B.7F
C. F D. F
2.已知在太阳系外某“宜居”行星的质量约为地球质量的6.4倍一个在地球表面重力为600 N的人在这个行星表面的重力将变为960 N。由此可推知,该行星的半径与地球半径之比约为( )
A.1 : 2 B.2 : 1 C.3 : 2 D.4 : 1
3.载人火箭竖直升空的加速度为a=50 m/s2某时刻运载舱中质量m=60 kg的航天员对座椅的压力测量值为3 060 N,已知地球表面的重力加速度为10 m/s2,3.16,设地球半径为R,以下判断正确的有( )
A.此时火箭距地面的高度约为3R
B.此时火箭内的航天员处于完全失重状态
C.此时航天员所处位置的重力加速度为1 m/s2
D.此时航天员受到地球的引力为3 060 N
