北师大版八年级数学下册第一章三角形的证明单元复习题(含解析)
文档属性
| 名称 | 北师大版八年级数学下册第一章三角形的证明单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 397.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 11:10:53 | ||
图片预览


文档简介
北师大版八年级数学下册第一章三角形的证明单元复习题
一、单选题
1.等腰三角形的底角是顶角的2倍,则底角度数为( )
A. B. C. D.
2.以下列各组线段为边作三角形,不能作出直角三角形的是( )
A.1,2, B.6,8,10
C.3,7,8 D.0.3,0.4,0.5
3.下列各组数中,能作为直角三角形三边长的是( )
A.1,2,3 B.4,5,6 C.,2, D.6,8,10
4.已知一个等腰三角形的三边长分别为3x-2,4x-3,7,则这个等腰三角形的周长为( )
A.23 B.19.5或23 C.9或23 D.9或19.5或23
5.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角中,则的度数是( )
A.32° B.62° C.58° D.68°
6.已知等腰三角形的一边等于3,一边等于6,则它的周长等于( )
A.12 B.15 C.12或15 D.15或18
7.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=8,则CD等于( )
A.3 B.4 C.5 D.6
8.如图,在△ABC中,AB=AC,∠B=52°,以点C为圆心,CA长为半径作弧交AB于点D,分别以点A和点D为圆心,大于AD的长为半径作弧,两弧相交于点E,作直线CE交AB于点F,则∠ACF的度数是( )
A.24° B.26° C.14° D.18°
9.如图,在△ABC中,∠B=∠C,AD为△ABC的中线,那么下列结论错误的是( )
A.△ABD≌△ACD B.AD为△ABC的高线
C.AD为△ABC的角平分线 D.△ABC是等边三角形
10.在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A.三边中垂线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
二、填空题
11.如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为 .
12.如图,在等边△ABC中,AD⊥BC,垂足为点D,AD=4,P是AD上一动点,E为AB的中点,连接PE,PB,则PB+PE的最小值为 .
13.等腰三角形有一个是50°,它的一条腰上的高与底边的夹角是 .
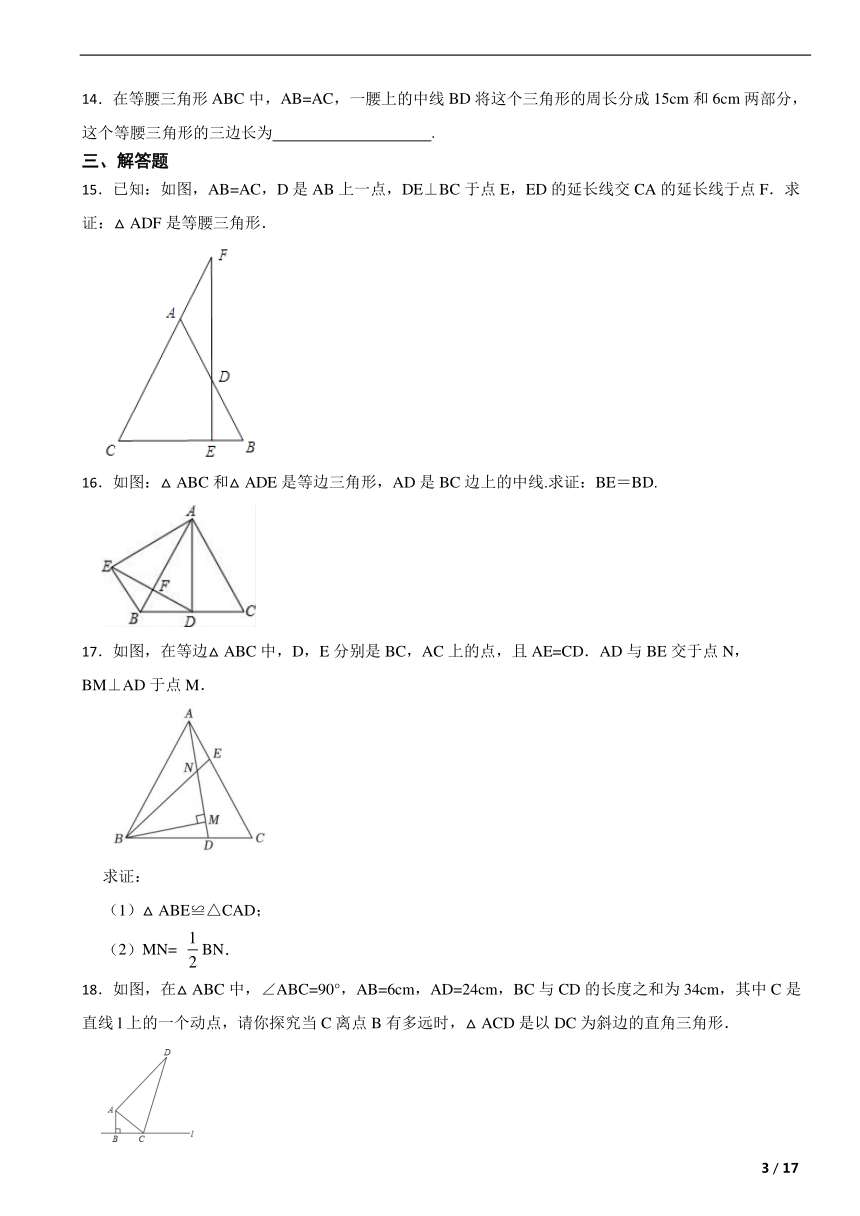
14.在等腰三角形ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的三边长为 .
三、解答题
15.已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.
16.如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.
17.如图,在等边△ABC中,D,E分别是BC,AC上的点,且AE=CD.AD与BE交于点N,BM⊥AD于点M.
求证:
(1)△ABE≌△CAD;
(2)MN= BN.
18.如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.
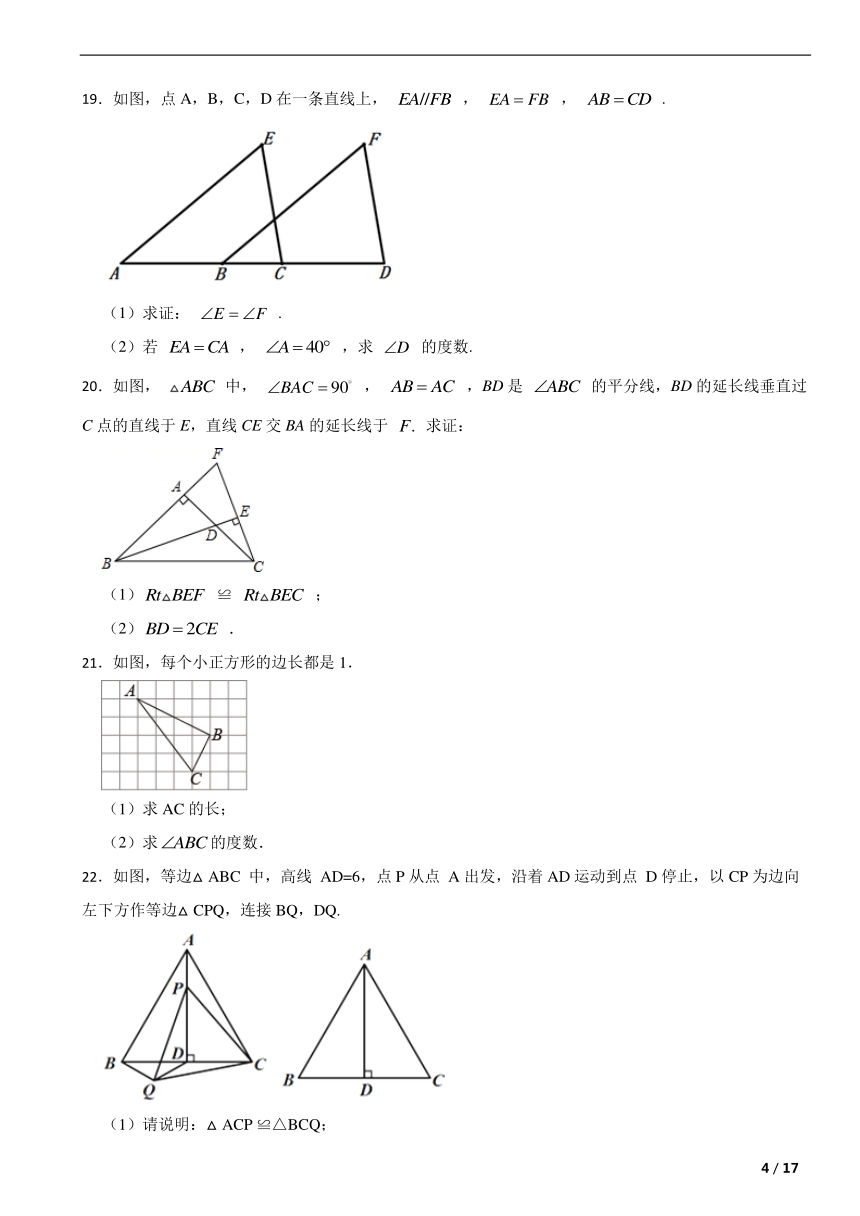
19.如图,点A,B,C,D在一条直线上, , , .
(1)求证: .
(2)若 , ,求 的度数.
20.如图, 中, , ,BD是 的平分线,BD的延长线垂直过C点的直线于E,直线CE交BA的延长线于 求证:
(1) ≌ ;
(2) .
21.如图,每个小正方形的边长都是1.
(1)求AC的长;
(2)求的度数.
22.如图,等边△ABC 中,高线 AD=6,点P从点 A出发,沿着AD运动到点 D停止,以CP为边向左下方作等边△CPQ,连接BQ,DQ.
(1)请说明:△ACP ≌△BCQ;
(2)在点P的运动过程中,当△BDQ是等腰三角形时,求∠BDQ的度数;
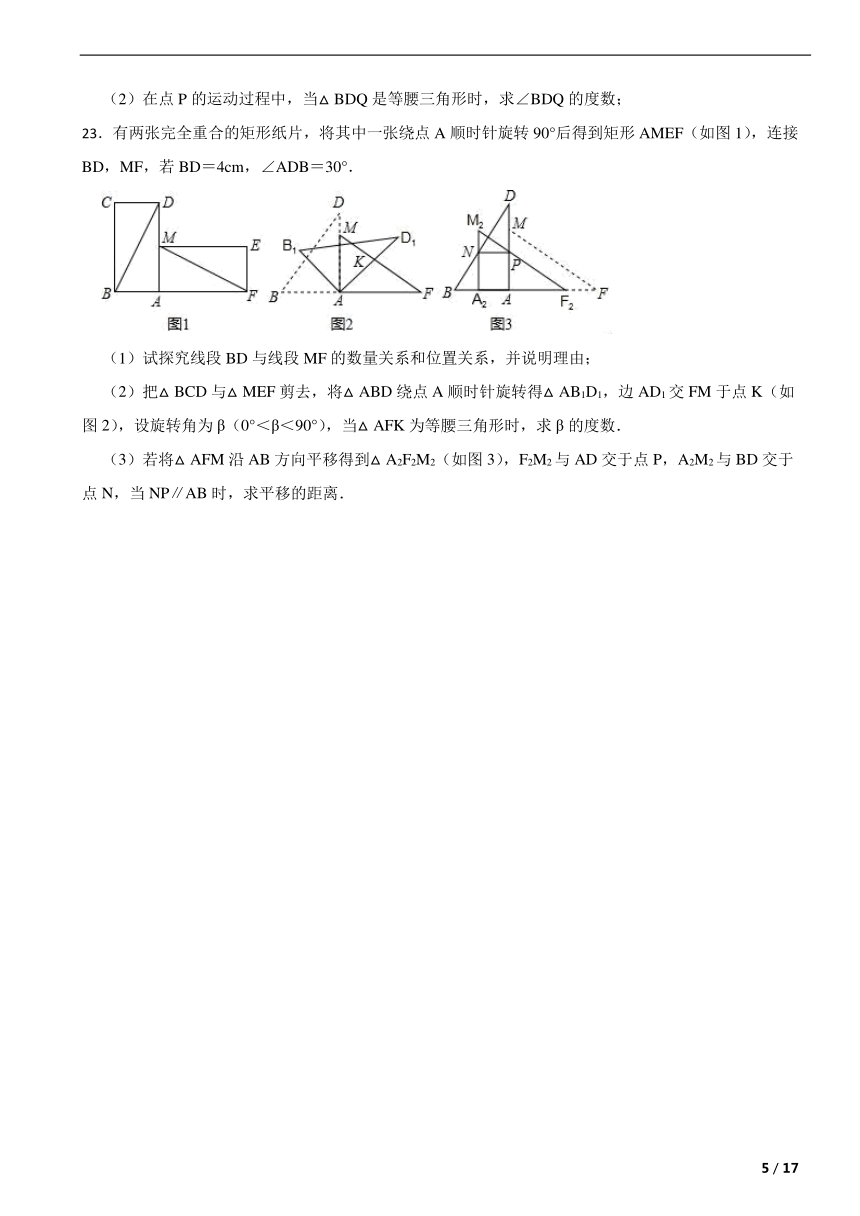
23.有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=4cm,∠ADB=30°.
(1)试探究线段BD与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD与△MEF剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求β的度数.
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
答案解析部分
1.【答案】D
【解析】【解答】∵等腰三角形中两底角相等,已知底角是顶角的2倍
∴在设等腰三角形的顶角度数为x时,则底角的度数为2x,
∵三角形内角和为 ,
∴得: ,解得: ,则 .
故答案为:D.
【分析】根据等腰三角形的性质以及三角形的内角和,利用方程求解即可.
2.【答案】C
【解析】【解答】解:A、∵ ,
∴以1,2, 为边的三角形是直角三角形,故本选项不符合题意;
B、∵62+82=36+64=100=102,
∴以6,8,10为边的三角形是直角三角形,故本选项不符合题意;
C、∵32+72=9+49=58≠82,
∴以3,7,8为边的三角形不是直角三角形,故本选项符合题意;
D、∵0.32+0.42=0.09+0.16=0.25=0.52,
∴以0.3,0.4,0.5为边的三角形是直角三角形,故本选项不符合题意.
故答案为:C.
【分析】若三角形的三边满足较小两边的平方和等于最大边长的平方,则该三角形为直角三角形,据此判断.
3.【答案】D
【解析】【解答】解:A. ,∴ 1,2,3 不能作为直角三角形三边长;
B. ,∴ 4,5,6不能作为直角三角形三边长 ;
C. ,∴ ,2, 不能作为直角三角形三边长;
D. ,∴ 6,8,10能作为直角三角形三边长 ;
故选D.
4.【答案】B
【解析】【解答】解:∵一个等腰三角形的三边长分别为3x-2,4x-3,7,
∴①当
即
∴这个等腰三角形的周长为:
②当
即
∴这个等腰三角形的周长为:
③当
即
∴该等腰三角形三边长为:1,1,7,不满足三角形三边关系定理,故舍去,
综上所述,这个等腰三角形的周长为:19.5或23,
故答案为:B.
【分析】根据等腰三角形形定义知需分情况讨论:①当②当③当分别求出x的值,判断是否满足三角形三边关系定理,进而即可计算出等腰三角形的周长.
5.【答案】C
【解析】【解答】解:在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠DEF=∠ABC=32°,
∴∠DFE=90°﹣32°=58°.
故答案为:C.
【分析】由题意根据HL定理可证Rt△ABC≌Rt△DEF,由全等三角形的对应角相等可得∠DEF=∠ABC,然后根据直角三角形两锐角互余可求解.
6.【答案】B
【解析】【解答】分两种情况讨论,
当三边为3,3,6时不能构成三角形,舍去;
当三边为3,6,6时,周长为15.
故答案为:B.
【分析】由于此题没有明确的告知谁是等腰三角形的底边,谁是等腰三角形的腰,故需要分类讨论:①当三边为3,3,6,②当三边为3,6,6时,两种情况分别根据三角形三边的关系判断能否围成三角形,能围成三角形的利用三角形周长的计算方法算出答案。
7.【答案】B
【解析】【解答】∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC,
∴∠CBD=∠DBA=30°,
∴BD=AD,
∵AD=8,
∴BD=8,
∴CD= BD=4.
故B符合题意.
故答案为:B.
【分析】根据题意可得∠A=30°,再由BD平分∠ABC,可得∠CBD=∠DBA=30°,根据含30°角的直角三角形的性质可求出CD的长.
8.【答案】C
【解析】【解答】解:由作图过程知:CF平分∠ACD,CA=CD,
在中,∠B=52°,AB=AC,
∴∠A=180°-2∠B=180°-2×52°=76°,
在等腰三角形ACD中,
∠ACD=180°-2∠A=180°-2×76°=28°,
∴∠ACF=。
故答案为:C.
【分析】首先由作图知,CF平分∠ACD,CA=CD,然后在等腰三角形ABC中,根据三角形内角和定理求得∠A=76°,然后再在等腰三角形ACD中,根据三角形内角和定理求得∠ACD=28°,进而根据角平分线的定义求得∠ACF=14°。
9.【答案】D
【解析】【解答】解:∵∠B=∠C,
∴AB=AC,
∵AD是△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD,即AD是△ABC的高,AD为△ABC的角平分线,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中
∴△ABD≌△ACD,
即选项A、B、C都正确,
根据已知只能推出AC=AB,不能推出AC、AB和BC的关系,
即不能得出△ABC是等边三角形,选项D错误,
故选D.
【分析】据等角对等边得出AC=AB,根据等腰三角形性质推出AD⊥BC,AD为△ABC的角平分线,根据AAS可以证出△ABD≌△ACD,根据以上结论推出即可.
10.【答案】A
【解析】【解答】解:∵三角形的三条垂直平分线的交点到中间的凳子的距离相等,
∴凳子应放在△ABC的三条垂直平分线的交点最适当.
故答案为:A.
【分析】根据垂直平分线的性质,线段垂直平分线上的点与线段的两个端点的距离相等,得到凳子应放的最适当的位置是在△ABC的三边垂直平分线的交点上.
11.【答案】4
【解析】【解答】∵AB=AC,AD⊥BC,
∴BD=DC,
∵AB+AC+BC=18,
即AB+BD+CD+AC=18,
∴AC+DC=9,
又∵AC+DC+AD=13,
∴AD ,
故答案为:4.
【分析】根据等腰三角形的性质作答即可。
12.【答案】4
【解析】【解答】解:连接EC交AD于点P,
∵△BAC是等边三角形,AD⊥BC,
∴AD垂直平分BC,
∴BP=CP,
∴PB+PE=PC+PE≥EC,
当E、P、C三点共线时,PB+PE的值最小,
∵E是AB的中点,AD⊥BC,
∴AD=EC,
∵AD=4,
∴EC=4,
∴PB+PE的最值为4,
故答案为:4.
【分析】连接EC交AD于点P,当E、P、C三点共线时,PB+PE的值最小,再求出EC=4,即可得到PB+PE的最值为4。
13.【答案】25°或40°
【解析】【解答】解:若50°是顶角,底角是65°,则它的一条腰上的高与底边的夹角是65°-40°=25°,
若50°是底角,顶角是80°,则它的一条腰上的高与底边的夹角是50°-10°=40°.
故答案为: 25°或40°
【分析】由于50°的角是锐角,故可以作等腰三角形的底角,也可以作为等腰三角形的顶角,所以需要分类讨论:①若50°是顶角,底角是65°,根据三角形的内角和及角的和差即可算出答案;②若50°是底角,顶角是80°,根据三角形的内角和及角的和差即可算出答案,综上所述即可得出答案。
14.【答案】10cm,10cm,1cm
【解析】【解答】 设等影三角形的腰长、底边长分别为,由题
意得
或解得或
故等腰三角形的三边分别为:3,6,6或者4,4,7,3+6>6,4+4>7,均符合三角形的三边关系,
故底边长为3cm或7cm.
【分析】分别设三角形的腰和底边分别为x cm和y cm,再根据等腰三角形的性质和题意列二元一次方程,再验证是否满足三角形的三边关系即可求得.
15.【答案】解:∵AB=AC,
∴∠B=∠C(等边对等角).
∵DE⊥BC于E,
∴∠FEB=∠FEC=90°,
∴∠B+∠EDB=∠C+∠EFC=90°,
∴∠EFC=∠EDB(等角的余角相等).
∵∠EDB=∠ADF(对顶角相等),
∴∠EFC=∠ADF.
∴△ADF是等腰三角形
【解析】【分析】先根据等腰三角形的性质得出∠B=∠C,再由等角的余角相等得出∠EFC=∠EDB,进而可得出∠EFC=∠ADF,由此可得出结论.
16.【答案】证明:等边三角形ABC中,因为 AD是BC边上的中线 ,
所以 AD为∠BAC的角平分线 ,
所以∠CAD=∠BAD=30°,
因为三角形ADE是等边三角形,
所以∠DAE=60°,
所以 ∠BAE=∠BAD=30° ,
在△ABE与△ABD中,
因为AE=AD, ∠BAE=∠BAD=30° ,AB=AB,
所以 △ABE≌△ABD (SAS),
所以BE=BD.
【解析】【分析】 根据等边三角形三线合一的性质可得AD为∠BAC的角平分线,根据等边三角形各内角为60°即可求得∠BAE=∠BAD=30°,进而证明△ABE≌△ABD,得BE=BD.
17.【答案】(1)证明:∵△ABC是等边三角形,∴AB=BC=AC,∠BAC=∠ACB= 60°,
在△ABE和△CAD中,
∴△ABE≌△CAD (SAS)
(2)证明:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BNM=∠BAN+∠ABN=∠BAN+∠CAD=60°,
∵BM⊥AD,
∴∠AMB=90°,
∴∠NBM=30°,
∴MN= BN
【解析】【分析】(1)根据等边三角形性质可得AB=BC=AC,∠BAC=∠ACB= 60°,再根据全等三角形判定定理即可求出答案.
(2)根据全等三角形性质可得∠ABE=∠CAD,则∠BNM=∠BAN+∠ABN=∠BAN+∠CAD=60°,再根据三角形内角和定理可得∠NBM=30°,再根据含30°角的直角三角形性质即可求出答案.
18.【答案】解:∵BC与CD的长度之和为34cm,
∴设BC=xcm,则CD=(34﹣x)cm.
∵在△ABC中,∠ABC=90°,AB=6cm,
∴AC2=AB2+BC2=62+x2.
∵△ACD是以DC为斜边的直角三角形,AD=24cm,
∴AC2=CD2﹣AD2=(34﹣x)2﹣242,
∴62+x2=(34﹣x)2﹣242,
解得x=8,
即BC=8cm
【解析】【分析】设BC=xcm,则CD=(34﹣x)cm,再根据勾股定理及勾股定理的逆定理列出方程,求出x的值即可.
19.【答案】(1)证明:
在 和 中
.
(2)解:
.
.
.
【解析】【分析】(1)根据平行线的性质得出∠A=∠EBD,根据线段的和差关系得出AC=BD,然后根据SAS求出△EAC≌△FBD,则可得出∠E=∠F;
(2)根据等腰三角形的性质和三角形内角和定理求出∠ACE的度数,然后利用全等三角形对应角相等,即可解答.
20.【答案】(1)证明: 是 的平分线,
,
,
,
在 和 中,
,
≌ ;
(2)证明: ≌ ,
,
,
,
,且 ,
, ,
,
,
在 和 中,
,
≌ ,
,
,
.
【解析】【分析】(1)求出 , ,根据ASA推出两三角形全等即可;(2)根据全等三角形性质求出 ,证 ≌ ,推出 即可.
21.【答案】(1)解:如图,取格点D,连接AD,CD,
则,,,
在中,根据勾股定理,.
∴(舍负);
(2)解:如图,取格点E,F,连接CE,BE,BF,AF,
则,,,,.
在中,根据勾股定理,.
在中,根据勾股定理,.
∴,
∴.
【解析】【分析】(1)利用勾股定理求出AC的长即可;
(2)根据勾股定理求出BC和AB的长,再利用勾股定理的逆定理可得
,即可证明
。
22.【答案】(1)解:∵△ABC和△PQC是等边三角形,
∴AC=BC,PC=QC,∠ACB=∠PCQ=60°,
又∵∠ACP=60°-∠BCP,∠BCQ=60°-∠BCP,
∴∠ACP=∠BCP
在△ACP和△BCQ中,
∴△ACP≌△BCQ(SAS).
(2)解:由(1)知,△ACP ≌△BCQ,
∴∠QBD=∠PAC=30°,
当△BDQ 是等腰三角形时,
①若BQ=QD,如图1,则∠BDQ=30°;
②若BQ=BD,如图2,则∠BDQ=75°;
③若BD=DQ,如图3,则∠BDQ=120°.
【解析】【分析】(1)根据等边三角形的性质可得AC=BC,PC=QC,∠ACB=∠PCQ=60°,根据角的和差关系可得∠ACP=∠BCP,然后根据全等三角形的判定定理进行证明;
(2)由(1)知:△ACP ≌△BCQ,则∠QBD=∠PAC=30°,①若BQ=QD,根据等腰三角形的性质可得∠BDQ的度数;②若BQ=BD,根据等腰三角形的性质以及内角和定理可得∠BDQ的度数;③若BD=DQ,同理可得∠BDQ的度数.
23.【答案】(1)解:结论:BD=MF,BD⊥MF.理由:
如图1,延长FM交BD于点N.
由题意得:△BAD≌△MAF,∴BD=MF,∠ADB=∠AFM.
又∵∠DMN=∠AMF,∴∠ADB+∠DMN=∠AFM+∠AMF=90°,∴∠DNM=90°,∴BD⊥MF.
(2)解:如图2. ①当AK=FK时,∠KAF=∠F=30°,则∠BAB1=180°﹣∠B1AD1﹣∠KAF=180°﹣90°﹣30°=60°,即β=60°;
②当AF=FK时,∠FAK (180°﹣∠F)=75°,∴∠BAB1=90°﹣∠FAK=15°,即β=15°;
综上所述:β的度数为60°或15°
(3)解:如图3. 由题意得矩形PNA2A.设A2A=x,则PN=x.在Rt△A2M2F2中,∵F2M2=FM=4,∠F=∠ADB=30°,∴A2M2=2,A2F2=2 ,∴AF2=2 x.
∵∠PAF2=90°,∠PF2A=30°,∴AP=AF2 tan30°=2 x,∴PD=AD﹣AP=2 2 x.
∵NP∥AB,∴∠DNP=∠B. ∵∠D=∠D,∴△DPN∽△DAB,∴ ,
∴ ,解得:x= ,即A2A= ,
∴平移的距离是( )cm.
【解析】【分析】(1)由旋转的性质得到BD=MF,△BAD≌△MAF,推出BD=MF,∠ADB=∠AFM=30°,进而可得∠DNM的大小.(2)分两种情形讨论①当AK=FK时,②当AF=FK时,根据旋转的性质得出结论.(3)求平移的距离是A2A的长度.在矩形PNA2A中,A2A=PN,只要求出PN的长度就行.用△DPN∽△DAB得出对应线段成比例,即可得到A2A的大小.
1 / 1
一、单选题
1.等腰三角形的底角是顶角的2倍,则底角度数为( )
A. B. C. D.
2.以下列各组线段为边作三角形,不能作出直角三角形的是( )
A.1,2, B.6,8,10
C.3,7,8 D.0.3,0.4,0.5
3.下列各组数中,能作为直角三角形三边长的是( )
A.1,2,3 B.4,5,6 C.,2, D.6,8,10
4.已知一个等腰三角形的三边长分别为3x-2,4x-3,7,则这个等腰三角形的周长为( )
A.23 B.19.5或23 C.9或23 D.9或19.5或23
5.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角中,则的度数是( )
A.32° B.62° C.58° D.68°
6.已知等腰三角形的一边等于3,一边等于6,则它的周长等于( )
A.12 B.15 C.12或15 D.15或18
7.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=8,则CD等于( )
A.3 B.4 C.5 D.6
8.如图,在△ABC中,AB=AC,∠B=52°,以点C为圆心,CA长为半径作弧交AB于点D,分别以点A和点D为圆心,大于AD的长为半径作弧,两弧相交于点E,作直线CE交AB于点F,则∠ACF的度数是( )
A.24° B.26° C.14° D.18°
9.如图,在△ABC中,∠B=∠C,AD为△ABC的中线,那么下列结论错误的是( )
A.△ABD≌△ACD B.AD为△ABC的高线
C.AD为△ABC的角平分线 D.△ABC是等边三角形
10.在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A.三边中垂线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
二、填空题
11.如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为 .
12.如图,在等边△ABC中,AD⊥BC,垂足为点D,AD=4,P是AD上一动点,E为AB的中点,连接PE,PB,则PB+PE的最小值为 .
13.等腰三角形有一个是50°,它的一条腰上的高与底边的夹角是 .
14.在等腰三角形ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的三边长为 .
三、解答题
15.已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.
16.如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.
17.如图,在等边△ABC中,D,E分别是BC,AC上的点,且AE=CD.AD与BE交于点N,BM⊥AD于点M.
求证:
(1)△ABE≌△CAD;
(2)MN= BN.
18.如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.
19.如图,点A,B,C,D在一条直线上, , , .
(1)求证: .
(2)若 , ,求 的度数.
20.如图, 中, , ,BD是 的平分线,BD的延长线垂直过C点的直线于E,直线CE交BA的延长线于 求证:
(1) ≌ ;
(2) .
21.如图,每个小正方形的边长都是1.
(1)求AC的长;
(2)求的度数.
22.如图,等边△ABC 中,高线 AD=6,点P从点 A出发,沿着AD运动到点 D停止,以CP为边向左下方作等边△CPQ,连接BQ,DQ.
(1)请说明:△ACP ≌△BCQ;
(2)在点P的运动过程中,当△BDQ是等腰三角形时,求∠BDQ的度数;
23.有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=4cm,∠ADB=30°.
(1)试探究线段BD与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD与△MEF剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求β的度数.
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
答案解析部分
1.【答案】D
【解析】【解答】∵等腰三角形中两底角相等,已知底角是顶角的2倍
∴在设等腰三角形的顶角度数为x时,则底角的度数为2x,
∵三角形内角和为 ,
∴得: ,解得: ,则 .
故答案为:D.
【分析】根据等腰三角形的性质以及三角形的内角和,利用方程求解即可.
2.【答案】C
【解析】【解答】解:A、∵ ,
∴以1,2, 为边的三角形是直角三角形,故本选项不符合题意;
B、∵62+82=36+64=100=102,
∴以6,8,10为边的三角形是直角三角形,故本选项不符合题意;
C、∵32+72=9+49=58≠82,
∴以3,7,8为边的三角形不是直角三角形,故本选项符合题意;
D、∵0.32+0.42=0.09+0.16=0.25=0.52,
∴以0.3,0.4,0.5为边的三角形是直角三角形,故本选项不符合题意.
故答案为:C.
【分析】若三角形的三边满足较小两边的平方和等于最大边长的平方,则该三角形为直角三角形,据此判断.
3.【答案】D
【解析】【解答】解:A. ,∴ 1,2,3 不能作为直角三角形三边长;
B. ,∴ 4,5,6不能作为直角三角形三边长 ;
C. ,∴ ,2, 不能作为直角三角形三边长;
D. ,∴ 6,8,10能作为直角三角形三边长 ;
故选D.
4.【答案】B
【解析】【解答】解:∵一个等腰三角形的三边长分别为3x-2,4x-3,7,
∴①当
即
∴这个等腰三角形的周长为:
②当
即
∴这个等腰三角形的周长为:
③当
即
∴该等腰三角形三边长为:1,1,7,不满足三角形三边关系定理,故舍去,
综上所述,这个等腰三角形的周长为:19.5或23,
故答案为:B.
【分析】根据等腰三角形形定义知需分情况讨论:①当②当③当分别求出x的值,判断是否满足三角形三边关系定理,进而即可计算出等腰三角形的周长.
5.【答案】C
【解析】【解答】解:在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠DEF=∠ABC=32°,
∴∠DFE=90°﹣32°=58°.
故答案为:C.
【分析】由题意根据HL定理可证Rt△ABC≌Rt△DEF,由全等三角形的对应角相等可得∠DEF=∠ABC,然后根据直角三角形两锐角互余可求解.
6.【答案】B
【解析】【解答】分两种情况讨论,
当三边为3,3,6时不能构成三角形,舍去;
当三边为3,6,6时,周长为15.
故答案为:B.
【分析】由于此题没有明确的告知谁是等腰三角形的底边,谁是等腰三角形的腰,故需要分类讨论:①当三边为3,3,6,②当三边为3,6,6时,两种情况分别根据三角形三边的关系判断能否围成三角形,能围成三角形的利用三角形周长的计算方法算出答案。
7.【答案】B
【解析】【解答】∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC,
∴∠CBD=∠DBA=30°,
∴BD=AD,
∵AD=8,
∴BD=8,
∴CD= BD=4.
故B符合题意.
故答案为:B.
【分析】根据题意可得∠A=30°,再由BD平分∠ABC,可得∠CBD=∠DBA=30°,根据含30°角的直角三角形的性质可求出CD的长.
8.【答案】C
【解析】【解答】解:由作图过程知:CF平分∠ACD,CA=CD,
在中,∠B=52°,AB=AC,
∴∠A=180°-2∠B=180°-2×52°=76°,
在等腰三角形ACD中,
∠ACD=180°-2∠A=180°-2×76°=28°,
∴∠ACF=。
故答案为:C.
【分析】首先由作图知,CF平分∠ACD,CA=CD,然后在等腰三角形ABC中,根据三角形内角和定理求得∠A=76°,然后再在等腰三角形ACD中,根据三角形内角和定理求得∠ACD=28°,进而根据角平分线的定义求得∠ACF=14°。
9.【答案】D
【解析】【解答】解:∵∠B=∠C,
∴AB=AC,
∵AD是△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD,即AD是△ABC的高,AD为△ABC的角平分线,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中
∴△ABD≌△ACD,
即选项A、B、C都正确,
根据已知只能推出AC=AB,不能推出AC、AB和BC的关系,
即不能得出△ABC是等边三角形,选项D错误,
故选D.
【分析】据等角对等边得出AC=AB,根据等腰三角形性质推出AD⊥BC,AD为△ABC的角平分线,根据AAS可以证出△ABD≌△ACD,根据以上结论推出即可.
10.【答案】A
【解析】【解答】解:∵三角形的三条垂直平分线的交点到中间的凳子的距离相等,
∴凳子应放在△ABC的三条垂直平分线的交点最适当.
故答案为:A.
【分析】根据垂直平分线的性质,线段垂直平分线上的点与线段的两个端点的距离相等,得到凳子应放的最适当的位置是在△ABC的三边垂直平分线的交点上.
11.【答案】4
【解析】【解答】∵AB=AC,AD⊥BC,
∴BD=DC,
∵AB+AC+BC=18,
即AB+BD+CD+AC=18,
∴AC+DC=9,
又∵AC+DC+AD=13,
∴AD ,
故答案为:4.
【分析】根据等腰三角形的性质作答即可。
12.【答案】4
【解析】【解答】解:连接EC交AD于点P,
∵△BAC是等边三角形,AD⊥BC,
∴AD垂直平分BC,
∴BP=CP,
∴PB+PE=PC+PE≥EC,
当E、P、C三点共线时,PB+PE的值最小,
∵E是AB的中点,AD⊥BC,
∴AD=EC,
∵AD=4,
∴EC=4,
∴PB+PE的最值为4,
故答案为:4.
【分析】连接EC交AD于点P,当E、P、C三点共线时,PB+PE的值最小,再求出EC=4,即可得到PB+PE的最值为4。
13.【答案】25°或40°
【解析】【解答】解:若50°是顶角,底角是65°,则它的一条腰上的高与底边的夹角是65°-40°=25°,
若50°是底角,顶角是80°,则它的一条腰上的高与底边的夹角是50°-10°=40°.
故答案为: 25°或40°
【分析】由于50°的角是锐角,故可以作等腰三角形的底角,也可以作为等腰三角形的顶角,所以需要分类讨论:①若50°是顶角,底角是65°,根据三角形的内角和及角的和差即可算出答案;②若50°是底角,顶角是80°,根据三角形的内角和及角的和差即可算出答案,综上所述即可得出答案。
14.【答案】10cm,10cm,1cm
【解析】【解答】 设等影三角形的腰长、底边长分别为,由题
意得
或解得或
故等腰三角形的三边分别为:3,6,6或者4,4,7,3+6>6,4+4>7,均符合三角形的三边关系,
故底边长为3cm或7cm.
【分析】分别设三角形的腰和底边分别为x cm和y cm,再根据等腰三角形的性质和题意列二元一次方程,再验证是否满足三角形的三边关系即可求得.
15.【答案】解:∵AB=AC,
∴∠B=∠C(等边对等角).
∵DE⊥BC于E,
∴∠FEB=∠FEC=90°,
∴∠B+∠EDB=∠C+∠EFC=90°,
∴∠EFC=∠EDB(等角的余角相等).
∵∠EDB=∠ADF(对顶角相等),
∴∠EFC=∠ADF.
∴△ADF是等腰三角形
【解析】【分析】先根据等腰三角形的性质得出∠B=∠C,再由等角的余角相等得出∠EFC=∠EDB,进而可得出∠EFC=∠ADF,由此可得出结论.
16.【答案】证明:等边三角形ABC中,因为 AD是BC边上的中线 ,
所以 AD为∠BAC的角平分线 ,
所以∠CAD=∠BAD=30°,
因为三角形ADE是等边三角形,
所以∠DAE=60°,
所以 ∠BAE=∠BAD=30° ,
在△ABE与△ABD中,
因为AE=AD, ∠BAE=∠BAD=30° ,AB=AB,
所以 △ABE≌△ABD (SAS),
所以BE=BD.
【解析】【分析】 根据等边三角形三线合一的性质可得AD为∠BAC的角平分线,根据等边三角形各内角为60°即可求得∠BAE=∠BAD=30°,进而证明△ABE≌△ABD,得BE=BD.
17.【答案】(1)证明:∵△ABC是等边三角形,∴AB=BC=AC,∠BAC=∠ACB= 60°,
在△ABE和△CAD中,
∴△ABE≌△CAD (SAS)
(2)证明:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BNM=∠BAN+∠ABN=∠BAN+∠CAD=60°,
∵BM⊥AD,
∴∠AMB=90°,
∴∠NBM=30°,
∴MN= BN
【解析】【分析】(1)根据等边三角形性质可得AB=BC=AC,∠BAC=∠ACB= 60°,再根据全等三角形判定定理即可求出答案.
(2)根据全等三角形性质可得∠ABE=∠CAD,则∠BNM=∠BAN+∠ABN=∠BAN+∠CAD=60°,再根据三角形内角和定理可得∠NBM=30°,再根据含30°角的直角三角形性质即可求出答案.
18.【答案】解:∵BC与CD的长度之和为34cm,
∴设BC=xcm,则CD=(34﹣x)cm.
∵在△ABC中,∠ABC=90°,AB=6cm,
∴AC2=AB2+BC2=62+x2.
∵△ACD是以DC为斜边的直角三角形,AD=24cm,
∴AC2=CD2﹣AD2=(34﹣x)2﹣242,
∴62+x2=(34﹣x)2﹣242,
解得x=8,
即BC=8cm
【解析】【分析】设BC=xcm,则CD=(34﹣x)cm,再根据勾股定理及勾股定理的逆定理列出方程,求出x的值即可.
19.【答案】(1)证明:
在 和 中
.
(2)解:
.
.
.
【解析】【分析】(1)根据平行线的性质得出∠A=∠EBD,根据线段的和差关系得出AC=BD,然后根据SAS求出△EAC≌△FBD,则可得出∠E=∠F;
(2)根据等腰三角形的性质和三角形内角和定理求出∠ACE的度数,然后利用全等三角形对应角相等,即可解答.
20.【答案】(1)证明: 是 的平分线,
,
,
,
在 和 中,
,
≌ ;
(2)证明: ≌ ,
,
,
,
,且 ,
, ,
,
,
在 和 中,
,
≌ ,
,
,
.
【解析】【分析】(1)求出 , ,根据ASA推出两三角形全等即可;(2)根据全等三角形性质求出 ,证 ≌ ,推出 即可.
21.【答案】(1)解:如图,取格点D,连接AD,CD,
则,,,
在中,根据勾股定理,.
∴(舍负);
(2)解:如图,取格点E,F,连接CE,BE,BF,AF,
则,,,,.
在中,根据勾股定理,.
在中,根据勾股定理,.
∴,
∴.
【解析】【分析】(1)利用勾股定理求出AC的长即可;
(2)根据勾股定理求出BC和AB的长,再利用勾股定理的逆定理可得
,即可证明
。
22.【答案】(1)解:∵△ABC和△PQC是等边三角形,
∴AC=BC,PC=QC,∠ACB=∠PCQ=60°,
又∵∠ACP=60°-∠BCP,∠BCQ=60°-∠BCP,
∴∠ACP=∠BCP
在△ACP和△BCQ中,
∴△ACP≌△BCQ(SAS).
(2)解:由(1)知,△ACP ≌△BCQ,
∴∠QBD=∠PAC=30°,
当△BDQ 是等腰三角形时,
①若BQ=QD,如图1,则∠BDQ=30°;
②若BQ=BD,如图2,则∠BDQ=75°;
③若BD=DQ,如图3,则∠BDQ=120°.
【解析】【分析】(1)根据等边三角形的性质可得AC=BC,PC=QC,∠ACB=∠PCQ=60°,根据角的和差关系可得∠ACP=∠BCP,然后根据全等三角形的判定定理进行证明;
(2)由(1)知:△ACP ≌△BCQ,则∠QBD=∠PAC=30°,①若BQ=QD,根据等腰三角形的性质可得∠BDQ的度数;②若BQ=BD,根据等腰三角形的性质以及内角和定理可得∠BDQ的度数;③若BD=DQ,同理可得∠BDQ的度数.
23.【答案】(1)解:结论:BD=MF,BD⊥MF.理由:
如图1,延长FM交BD于点N.
由题意得:△BAD≌△MAF,∴BD=MF,∠ADB=∠AFM.
又∵∠DMN=∠AMF,∴∠ADB+∠DMN=∠AFM+∠AMF=90°,∴∠DNM=90°,∴BD⊥MF.
(2)解:如图2. ①当AK=FK时,∠KAF=∠F=30°,则∠BAB1=180°﹣∠B1AD1﹣∠KAF=180°﹣90°﹣30°=60°,即β=60°;
②当AF=FK时,∠FAK (180°﹣∠F)=75°,∴∠BAB1=90°﹣∠FAK=15°,即β=15°;
综上所述:β的度数为60°或15°
(3)解:如图3. 由题意得矩形PNA2A.设A2A=x,则PN=x.在Rt△A2M2F2中,∵F2M2=FM=4,∠F=∠ADB=30°,∴A2M2=2,A2F2=2 ,∴AF2=2 x.
∵∠PAF2=90°,∠PF2A=30°,∴AP=AF2 tan30°=2 x,∴PD=AD﹣AP=2 2 x.
∵NP∥AB,∴∠DNP=∠B. ∵∠D=∠D,∴△DPN∽△DAB,∴ ,
∴ ,解得:x= ,即A2A= ,
∴平移的距离是( )cm.
【解析】【分析】(1)由旋转的性质得到BD=MF,△BAD≌△MAF,推出BD=MF,∠ADB=∠AFM=30°,进而可得∠DNM的大小.(2)分两种情形讨论①当AK=FK时,②当AF=FK时,根据旋转的性质得出结论.(3)求平移的距离是A2A的长度.在矩形PNA2A中,A2A=PN,只要求出PN的长度就行.用△DPN∽△DAB得出对应线段成比例,即可得到A2A的大小.
1 / 1
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
