北师大版七年级数学第二章实数单元复习题(含解析)
文档属性
| 名称 | 北师大版七年级数学第二章实数单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 295.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览




文档简介
北师大版七年级数学第二章实数单元复习题
一、单选题
1.3.61的平方根是( )
A.-1.9 B.1.9 C.±1.9 D.不存在
2.下列各数中,是无理数的是( )
A. B.(﹣π)0 C. D.
3.二次根式 有意义的x的范围是( )
A.x=1 B.x≠1 C.x≥1 D.x≤1
4.下列根式是最简二次根式的是( )
A. B. C. D.
5. 的算术平方根是( )
A. B. C. D.
6.对于任意实数x,下列各式中一定成立的是( )
A. B.=x+1
C.= D. =6
7.下列实数中,是无理数的是( )
A.-5 B. C. D.
8.估计 的值在( )
A.3和3.5之间 B.2.5和3之间 C.2和2.5之间 D.1.5和2之间
9.规定用符号[x]表示一个数的整数部分,例如[9.54]=9,[ ]=1,则[ ]的值为( )
A.5 B.6 C.7 D.8
10.用如图所示的计算器求的值,以下按键顺序不能求出符合题意结果的是( )
A.
B.
C.
D.
二、填空题
11.计算:( + )﹣ 的结果是 .
12.在实数范围内定义一种新运算“ ”,其运算规则为:a b=﹣2ab,如:1 5=﹣2×1×5=﹣10,则式子 = .
13.有一个数值转换器,原理如图所示,则当输入的x为4时,输出的y的值是
14.若a 2<b,a,b是两个连续的整数,则b= .
三、解答题
15.请把下列各数填入相应的集合中
,5.2,0,2π, ,﹣22, ,2005,﹣0.030030003…
正数集合:{ …}
负数集合:{ …}
无理数集合:{ …}
有理数集合:{ …}.
16.求下列各式中的x:
(1)2x2﹣1=9;
(2)﹣27(x﹣1)3=64.
17.若a、b互为相反数,c、d互为倒数,m的绝对值为2,求代数式 的值.
18.已知:的立方根是,,c是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
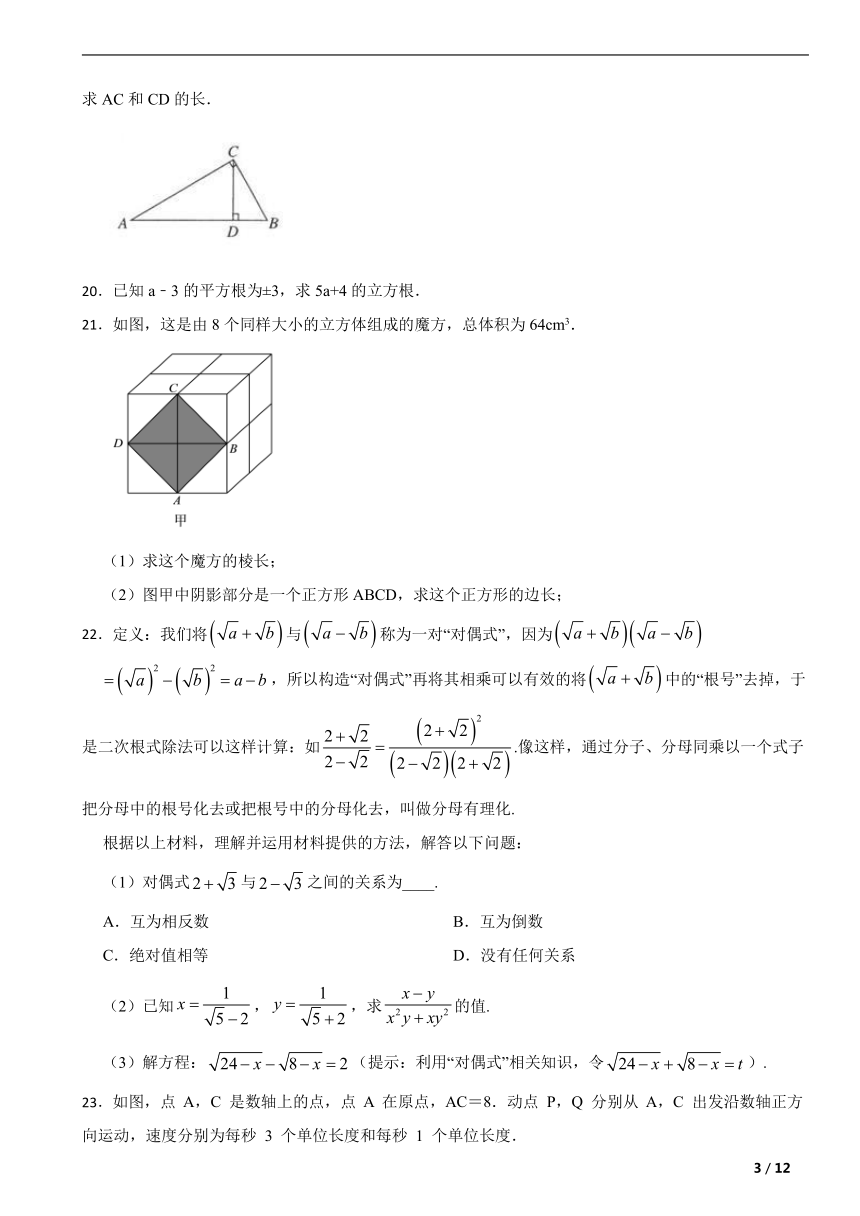
19.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.若S△ABC=3 cm2 ,BC= cm,求AC和CD的长.
20.已知a﹣3的平方根为±3,求5a+4的立方根.
21.如图,这是由8个同样大小的立方体组成的魔方,总体积为64cm3.
(1)求这个魔方的棱长;
(2)图甲中阴影部分是一个正方形ABCD,求这个正方形的边长;
22.定义:我们将与称为一对“对偶式”,因为
,所以构造“对偶式”再将其相乘可以有效的将中的“根号”去掉,于是二次根式除法可以这样计算:如.像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)对偶式与之间的关系为____.
A.互为相反数 B.互为倒数
C.绝对值相等 D.没有任何关系
(2)已知,,求的值.
(3)解方程:(提示:利用“对偶式”相关知识,令).
23.如图,点 A,C 是数轴上的点,点 A 在原点,AC=8.动点 P,Q 分别从 A,C 出发沿数轴正方向运动,速度分别为每秒 3 个单位长度和每秒 1 个单位长度.
设运动时间为t秒(t>0),解答下列问题:
(1)点C表示的数是 ;点P表示的数是 ,点Q表示的数是 .(点P,点 Q 表示的数用含 t 的式子表示)
(2)若点 M 是 AP 的中点,点 N 是 CQ 的中点,求 MN 的长.
(3)直接写出t为何值时,点P与点Q相距4个单位长度.
答案解析部分
1.【答案】C
【解析】【分析】根据平方根的定义进行求解.
【解答】∵(±1.9)2=3.61,
∴3.61的平方根是±=±1.9.
故答案为:C.
【点评】本题考查了平方根,一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根
2.【答案】A
【解析】【解答】解:A、=是无理数,
B、(﹣π)0=1是有理数,
C、是有理数,故C错误;
D、=8是有理数,故D错误;
故选:A.
【分析】根据无理数是无限不循环小数,可得答案.
3.【答案】D
【解析】【解答】解:依题可得:
1-x≥0,
解得:x≤1.
故答案为:D.
【分析】根据二次根式有意义的条件:根号里面的数应大于或等于0,列出不等式,解之即可得出答案.
4.【答案】C
【解析】【解答】解:A. = ,不符合题意;
B. = ,不符合题意;
C. 是最简二次根式,符合题意;
D. = 不符合题意.
故答案为:C.
【分析】根据最简二次根式的定义对各选项分析判断后利用排除法求解.
5.【答案】D
【解析】【解答】解:∵ ,
∴ 的算术的平方根是 .
故答案为:D.
【分析】利用算术平方根的计算方法求解即可。
6.【答案】D
【解析】【解答】解:当x≥1时,,A错误;
当x≥1时,=x+1,B错误;
= ,C错误;
=6x2,D正确.
故选:D.
【分析】根据二次根式的乘除法法则和二次根式的性质进行判断即可.
7.【答案】B
【解析】【解答】解:A. -5是有理数,故该选项不符合题意;
B. 是无理数,故该选项符合题意;
C. =2是有理数,故该选项不符合题意;
D. 是有理数,故该选项不符合题意
故答案为:B.
【分析】根据无理数的定义求解即可。
8.【答案】A
【解析】【解答】解:
=2+
= ;
∵4<5<6.25,
∴2< <2.5,
∴3< <3.5,
即 的值在3和3.5之间.
故答案为:A.
【分析】先利用二次根式混合运算求解,再估算大小即可。
9.【答案】B
【解析】【解答】解:≈3×2.232=6.696
∴原式的值为6.
故答案为:B。
【分析】根据题意估算的值,取该数的整数部分即可。
10.【答案】B
【解析】【解答】解:按键顺序依次为2,÷,7,2nd键,,=.
(由于计算器的类型很多,可根据计算器的说明书使用)
故答案为:B
【分析】根据题意求出按键顺序依次为2,÷,7,2nd键,,=.即可作答。
11.【答案】
【解析】【解答】解:( + )﹣ = + ﹣ = ,
故答案为:
【分析】用去括号法则以及合并同类项计算即可。
12.【答案】﹣2
【解析】【解答】解:根据题中的新定义得:原式=﹣2× × =﹣2,
故答案为:﹣2
【分析】原式利用题中的新定义计算即可得到结果.
13.【答案】
【解析】【解答】解:当x=4时,
y==2,
∵2是有理数,
∴x=2,
∴y=,
∵是无理数,
∴输出的y的值是:.
故答案为:.
【分析】根据流程图分步计算,先计算x的算术平方根,如果是有理数则返回,继续计算其算术平方根,直到结果是无理数为止.
14.【答案】1
【解析】【解答】解:∵2< <3,
∴0< -2<1,
∵a< -2<b,a,b是两个连续的整数,
∴b=1,
故答案为:1.
【分析】先估算出的大小,再求解即可。
15.【答案】解:正数集合{ }
负数集合{ }
无理数集合{2π,﹣0.030030003…}
有理数集合{ }
故答案为:{ },{ },{2π,﹣0.030030003…},{ }
【解析】【分析】利用实数的分类判定即可.
16.【答案】(1)解:2x2﹣1=9,
2x2=10,
x2=5,
解得x=﹣ 或
(2)解:﹣27(x﹣1)3=64,
(x﹣1)3=﹣ ,
x﹣1=﹣ ,
x=﹣
【解析】【分析】(1)先移项,再系数化为1,再开平方法进行解答;(2)先系数化为1,再开立方法进行解答.
17.【答案】解:∵a、b互为相反数,c、d互为倒数,m的绝对值为2
∴
原式= =3
【解析】【分析】利用相反数,倒数,以及绝对值的代数意义求出a+b,cd,以及m的值,代入原式计算即可得到结果.
18.【答案】(1)解:的立方根是,,
,,
∴,
即,,
又,
的整数部分,
即,,
(2)解:当,,时,
,
的平方根是
【解析】【分析】(1)根据立方根的性质求出a的值,利用同底数幂的乘法计算方法求出b的值,利用估算无理数的方法求出c的值即可;
(2)将a、b、c的值代入计算即可。
19.【答案】解:∵
∴ 在中, cm
∵
∴
【解析】【分析】利用三角形面积公式,容易得出,利用勾股定理,得出,然后再利用三角形面积公式,得出,最后得出答案。
20.【答案】解:由题意得:a﹣3=9,即a=12,
则5a+4=64,64的立方根为4.
【解析】【分析】利用平方根定义求出a的值,代入原式求出立方根即可.
21.【答案】(1)解:设这个魔方的棱长为xcm,由题意得:x3=64,解得x=4,
∴这个魔方的棱长为4cm.
(2)解:设正方形ABCD的边长为acm,
由题意得: 由(1)得AC=BD=4cm,
∴魔方的一个面的面积=4×4=16cm2,
又∵阴影部分的面积是魔方一个面的面积的一半,
∴,
∴
∴正方形ABCD的边长为.
【解析】【分析】(1)根据题意求出 x3=64, 再求解即可;
(2)先求出 魔方的一个面的面积=4×4=16cm2, 再求出 , 最后求解即可。
22.【答案】(1)B
(2)解:由题意得=,=,
∴x+y=2,x-y=4,xy=1,
∴;
(3)解:令,则两边同乘以,得
24-x-(8-x)=2t,
解得t=8,
∵①,②,
∴①+②,得=10,
两边同时平方得4(24-x)=100,
解得x=-1,
经检验,x=-1是原方程的解.
【解析】【解答】解:(1)∵()×()=4-3=1,
∴对偶数与之间的关系是互为倒数,
故答案为:B;
【分析】(1)根据平方差公式可得()×()=4-3=1,然后根据乘积为1的两个数互为倒数进行判断;
(2)分母有理化可得x=+2,y=-2,则x+y=2,x-y=4,xy=1,将待求式变形为,然后代入进行计算;
(3)令,则两边同乘以,得24-x-(8-x)=2t,求出t的值,即为的值,进而进行计算可得x的值.
23.【答案】(1)8;3t;8+t
(2)解:根据题意,得 , , ,AQ=8+t
∵点M是AP的中点,点N是CQ的中点,
∴ , ,
∴ ,
∴ ;
(3)解:由题意得 ,AQ=8+t,
∴ ,
解得t=2或6.
∴当t=2或6时点P与点Q相距4个单位长度.
【解析】【解答】解:(1)由题意可知,AP=3t,CQ=t,AC=8,A在原点,
∴点C表示的数为8,P表示的数为3t,Q表示的数为8+t,
故答案为:8,3t,8+t;
【分析】(1)由题意可知,AP=3t,CQ=t,AC=8,A在原点,则点C表示出的数为8,P表述出的数为3t,Q表示的数为8+t;
(2)根据题意,得出 , , ,AQ=8+t ,则 , , 则 ;
(3)由题意得出 ,AQ=8+t, 则 , 求解即可。
1 / 1
一、单选题
1.3.61的平方根是( )
A.-1.9 B.1.9 C.±1.9 D.不存在
2.下列各数中,是无理数的是( )
A. B.(﹣π)0 C. D.
3.二次根式 有意义的x的范围是( )
A.x=1 B.x≠1 C.x≥1 D.x≤1
4.下列根式是最简二次根式的是( )
A. B. C. D.
5. 的算术平方根是( )
A. B. C. D.
6.对于任意实数x,下列各式中一定成立的是( )
A. B.=x+1
C.= D. =6
7.下列实数中,是无理数的是( )
A.-5 B. C. D.
8.估计 的值在( )
A.3和3.5之间 B.2.5和3之间 C.2和2.5之间 D.1.5和2之间
9.规定用符号[x]表示一个数的整数部分,例如[9.54]=9,[ ]=1,则[ ]的值为( )
A.5 B.6 C.7 D.8
10.用如图所示的计算器求的值,以下按键顺序不能求出符合题意结果的是( )
A.
B.
C.
D.
二、填空题
11.计算:( + )﹣ 的结果是 .
12.在实数范围内定义一种新运算“ ”,其运算规则为:a b=﹣2ab,如:1 5=﹣2×1×5=﹣10,则式子 = .
13.有一个数值转换器,原理如图所示,则当输入的x为4时,输出的y的值是
14.若a 2<b,a,b是两个连续的整数,则b= .
三、解答题
15.请把下列各数填入相应的集合中
,5.2,0,2π, ,﹣22, ,2005,﹣0.030030003…
正数集合:{ …}
负数集合:{ …}
无理数集合:{ …}
有理数集合:{ …}.
16.求下列各式中的x:
(1)2x2﹣1=9;
(2)﹣27(x﹣1)3=64.
17.若a、b互为相反数,c、d互为倒数,m的绝对值为2,求代数式 的值.
18.已知:的立方根是,,c是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
19.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.若S△ABC=3 cm2 ,BC= cm,求AC和CD的长.
20.已知a﹣3的平方根为±3,求5a+4的立方根.
21.如图,这是由8个同样大小的立方体组成的魔方,总体积为64cm3.
(1)求这个魔方的棱长;
(2)图甲中阴影部分是一个正方形ABCD,求这个正方形的边长;
22.定义:我们将与称为一对“对偶式”,因为
,所以构造“对偶式”再将其相乘可以有效的将中的“根号”去掉,于是二次根式除法可以这样计算:如.像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)对偶式与之间的关系为____.
A.互为相反数 B.互为倒数
C.绝对值相等 D.没有任何关系
(2)已知,,求的值.
(3)解方程:(提示:利用“对偶式”相关知识,令).
23.如图,点 A,C 是数轴上的点,点 A 在原点,AC=8.动点 P,Q 分别从 A,C 出发沿数轴正方向运动,速度分别为每秒 3 个单位长度和每秒 1 个单位长度.
设运动时间为t秒(t>0),解答下列问题:
(1)点C表示的数是 ;点P表示的数是 ,点Q表示的数是 .(点P,点 Q 表示的数用含 t 的式子表示)
(2)若点 M 是 AP 的中点,点 N 是 CQ 的中点,求 MN 的长.
(3)直接写出t为何值时,点P与点Q相距4个单位长度.
答案解析部分
1.【答案】C
【解析】【分析】根据平方根的定义进行求解.
【解答】∵(±1.9)2=3.61,
∴3.61的平方根是±=±1.9.
故答案为:C.
【点评】本题考查了平方根,一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根
2.【答案】A
【解析】【解答】解:A、=是无理数,
B、(﹣π)0=1是有理数,
C、是有理数,故C错误;
D、=8是有理数,故D错误;
故选:A.
【分析】根据无理数是无限不循环小数,可得答案.
3.【答案】D
【解析】【解答】解:依题可得:
1-x≥0,
解得:x≤1.
故答案为:D.
【分析】根据二次根式有意义的条件:根号里面的数应大于或等于0,列出不等式,解之即可得出答案.
4.【答案】C
【解析】【解答】解:A. = ,不符合题意;
B. = ,不符合题意;
C. 是最简二次根式,符合题意;
D. = 不符合题意.
故答案为:C.
【分析】根据最简二次根式的定义对各选项分析判断后利用排除法求解.
5.【答案】D
【解析】【解答】解:∵ ,
∴ 的算术的平方根是 .
故答案为:D.
【分析】利用算术平方根的计算方法求解即可。
6.【答案】D
【解析】【解答】解:当x≥1时,,A错误;
当x≥1时,=x+1,B错误;
= ,C错误;
=6x2,D正确.
故选:D.
【分析】根据二次根式的乘除法法则和二次根式的性质进行判断即可.
7.【答案】B
【解析】【解答】解:A. -5是有理数,故该选项不符合题意;
B. 是无理数,故该选项符合题意;
C. =2是有理数,故该选项不符合题意;
D. 是有理数,故该选项不符合题意
故答案为:B.
【分析】根据无理数的定义求解即可。
8.【答案】A
【解析】【解答】解:
=2+
= ;
∵4<5<6.25,
∴2< <2.5,
∴3< <3.5,
即 的值在3和3.5之间.
故答案为:A.
【分析】先利用二次根式混合运算求解,再估算大小即可。
9.【答案】B
【解析】【解答】解:≈3×2.232=6.696
∴原式的值为6.
故答案为:B。
【分析】根据题意估算的值,取该数的整数部分即可。
10.【答案】B
【解析】【解答】解:按键顺序依次为2,÷,7,2nd键,,=.
(由于计算器的类型很多,可根据计算器的说明书使用)
故答案为:B
【分析】根据题意求出按键顺序依次为2,÷,7,2nd键,,=.即可作答。
11.【答案】
【解析】【解答】解:( + )﹣ = + ﹣ = ,
故答案为:
【分析】用去括号法则以及合并同类项计算即可。
12.【答案】﹣2
【解析】【解答】解:根据题中的新定义得:原式=﹣2× × =﹣2,
故答案为:﹣2
【分析】原式利用题中的新定义计算即可得到结果.
13.【答案】
【解析】【解答】解:当x=4时,
y==2,
∵2是有理数,
∴x=2,
∴y=,
∵是无理数,
∴输出的y的值是:.
故答案为:.
【分析】根据流程图分步计算,先计算x的算术平方根,如果是有理数则返回,继续计算其算术平方根,直到结果是无理数为止.
14.【答案】1
【解析】【解答】解:∵2< <3,
∴0< -2<1,
∵a< -2<b,a,b是两个连续的整数,
∴b=1,
故答案为:1.
【分析】先估算出的大小,再求解即可。
15.【答案】解:正数集合{ }
负数集合{ }
无理数集合{2π,﹣0.030030003…}
有理数集合{ }
故答案为:{ },{ },{2π,﹣0.030030003…},{ }
【解析】【分析】利用实数的分类判定即可.
16.【答案】(1)解:2x2﹣1=9,
2x2=10,
x2=5,
解得x=﹣ 或
(2)解:﹣27(x﹣1)3=64,
(x﹣1)3=﹣ ,
x﹣1=﹣ ,
x=﹣
【解析】【分析】(1)先移项,再系数化为1,再开平方法进行解答;(2)先系数化为1,再开立方法进行解答.
17.【答案】解:∵a、b互为相反数,c、d互为倒数,m的绝对值为2
∴
原式= =3
【解析】【分析】利用相反数,倒数,以及绝对值的代数意义求出a+b,cd,以及m的值,代入原式计算即可得到结果.
18.【答案】(1)解:的立方根是,,
,,
∴,
即,,
又,
的整数部分,
即,,
(2)解:当,,时,
,
的平方根是
【解析】【分析】(1)根据立方根的性质求出a的值,利用同底数幂的乘法计算方法求出b的值,利用估算无理数的方法求出c的值即可;
(2)将a、b、c的值代入计算即可。
19.【答案】解:∵
∴ 在中, cm
∵
∴
【解析】【分析】利用三角形面积公式,容易得出,利用勾股定理,得出,然后再利用三角形面积公式,得出,最后得出答案。
20.【答案】解:由题意得:a﹣3=9,即a=12,
则5a+4=64,64的立方根为4.
【解析】【分析】利用平方根定义求出a的值,代入原式求出立方根即可.
21.【答案】(1)解:设这个魔方的棱长为xcm,由题意得:x3=64,解得x=4,
∴这个魔方的棱长为4cm.
(2)解:设正方形ABCD的边长为acm,
由题意得: 由(1)得AC=BD=4cm,
∴魔方的一个面的面积=4×4=16cm2,
又∵阴影部分的面积是魔方一个面的面积的一半,
∴,
∴
∴正方形ABCD的边长为.
【解析】【分析】(1)根据题意求出 x3=64, 再求解即可;
(2)先求出 魔方的一个面的面积=4×4=16cm2, 再求出 , 最后求解即可。
22.【答案】(1)B
(2)解:由题意得=,=,
∴x+y=2,x-y=4,xy=1,
∴;
(3)解:令,则两边同乘以,得
24-x-(8-x)=2t,
解得t=8,
∵①,②,
∴①+②,得=10,
两边同时平方得4(24-x)=100,
解得x=-1,
经检验,x=-1是原方程的解.
【解析】【解答】解:(1)∵()×()=4-3=1,
∴对偶数与之间的关系是互为倒数,
故答案为:B;
【分析】(1)根据平方差公式可得()×()=4-3=1,然后根据乘积为1的两个数互为倒数进行判断;
(2)分母有理化可得x=+2,y=-2,则x+y=2,x-y=4,xy=1,将待求式变形为,然后代入进行计算;
(3)令,则两边同乘以,得24-x-(8-x)=2t,求出t的值,即为的值,进而进行计算可得x的值.
23.【答案】(1)8;3t;8+t
(2)解:根据题意,得 , , ,AQ=8+t
∵点M是AP的中点,点N是CQ的中点,
∴ , ,
∴ ,
∴ ;
(3)解:由题意得 ,AQ=8+t,
∴ ,
解得t=2或6.
∴当t=2或6时点P与点Q相距4个单位长度.
【解析】【解答】解:(1)由题意可知,AP=3t,CQ=t,AC=8,A在原点,
∴点C表示的数为8,P表示的数为3t,Q表示的数为8+t,
故答案为:8,3t,8+t;
【分析】(1)由题意可知,AP=3t,CQ=t,AC=8,A在原点,则点C表示出的数为8,P表述出的数为3t,Q表示的数为8+t;
(2)根据题意,得出 , , ,AQ=8+t ,则 , , 则 ;
(3)由题意得出 ,AQ=8+t, 则 , 求解即可。
1 / 1
