北师大版七年级数学下册第一章整式的乘除单元复习题(含解析)
文档属性
| 名称 | 北师大版七年级数学下册第一章整式的乘除单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 175.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 11:27:20 | ||
图片预览




文档简介
北师大版七年级数学下册第一章整式的乘除单元复习题
一、单选题
1.a6÷a2的结果是( )
A.a3 B.a4 C.a8 D.a12
2.下列计算正确的是( )
A.x2+x2=x4 B.(x﹣y)2=x2﹣y2
C.(x2y)3=x6y D.(﹣x)2x3=x5
3.下列运算正确的是( )
A.x2 x4=x8 B.3x+2y=6xy
C.(﹣x3)2=x6 D.y3÷y3=y
4.下列各运算中,计算正确的是( )
A.2a 3a=6a B.(3a2)3=27a6
C.a4÷a2=2a D.(a+b)2=a2+ab+b2
5.计算 的结果是( )
A.﹣1 B. C.0 D.1
6.下列运算正确的是( )
A.(ab)5=ab5 B.a8÷a2=a6
C.(a2)3=a5 D.(a﹣b)2=a2﹣b2
7. 下列计算正确的是( )
A.a5 a3=2a8 B.a3+a3=a6 C.(a3)2=a5 D.a5÷a3=a2
8.下面计算结果等于m6的是( )
A.m3 m2 B.(m3)2 C.m12÷m2 D.m6 m
9.PM 2.5是指大气中直径小于或等于0.0000025 m的颗粒物,将0.0000025用科学记数法表示为( )
A.0.25×10-5 B.0.25×10-6 C.2.5×10-6 D.2.5×10-5
10.若1+2+3+…+k之和为一完全平方n2,若n小于100,则k可能的值为( )
A.8 B.1,8 C.8,49 D.1,8,49.
二、填空题
11.数0.00035用科学记数法表示为 .
12.已知 ,则 .
13.已知,则 .
14. 已知当x=﹣3时,ax3﹣bx+5=9,则x=3时,ax3﹣bx+9的值为 .
三、解答题
15.a+b=5,ab=-2,求:和的值.
16.计算:
(1)( )﹣1+2×(﹣2)﹣2-(﹣π+3.14)0﹣( )﹣3
(2)用简便方法计算:1252﹣124×126﹣4101×(﹣0.25)99.
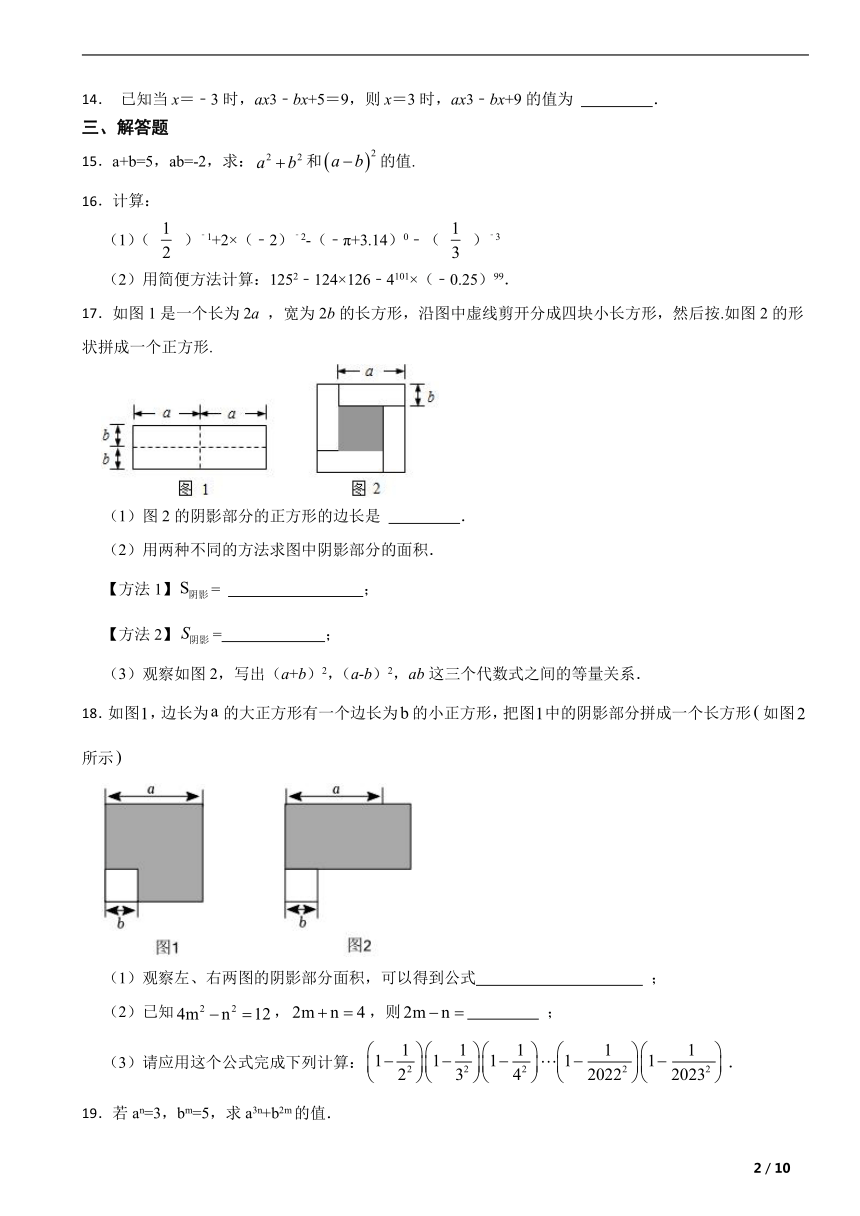
17.如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按.如图2的形状拼成一个正方形.
(1)图2的阴影部分的正方形的边长是 .
(2)用两种不同的方法求图中阴影部分的面积.
【方法1】= ;
【方法2】= ;
(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
18.如图,边长为的大正方形有一个边长为的小正方形,把图中的阴影部分拼成一个长方形如图所示
(1)观察左、右两图的阴影部分面积,可以得到公式 ;
(2)已知,,则 ;
(3)请应用这个公式完成下列计算:.
19.若an=3,bm=5,求a3n+b2m的值.
四、综合题
20.已知3a=4,3b=5,3c=8.
(1)填空:32a= ;3b+c的值为 ;
(2)求32a﹣3b的值.
21.在计算时,甲把错看成了6,得到结果是:,
(1)求出a的值;
(2)在(1)的条件下,且时,计算的结果.
22.某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.
(1)活动场所和花草的面积各是多少;
(2)整座健身馆的面积是成年人活动场所面积的多少倍.
23.从边长为 a 的正方形剪掉一个边长为 b 的正方形(如图 1),然后将剩余部分拼成一个长方形(如图 2).
(1)上述操作能验证的等式是_______(请选择正确的一个)
A.a2﹣2ab+b2 =(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2 +ab=a(a+b)
(2)若 x2 ﹣9y2=12,x+3y=4,求 x﹣3y 的值;
(3)计算: .
答案解析部分
1.【答案】B
【解析】【解答】解:,
故答案为:B.
【分析】利用同底数幂的除法的计算法则求解即可。
2.【答案】D
【解析】【解答】解:A、x2+x2=2x2,故该选项不正确,不符合题意;
B、 (x﹣y)2=x2-2xy+y2,故该选项不正确,不符合题意;
C、(x2y)3=x6y3,故该选项不正确,不符合题意;
D、 (﹣x)2x3=x5故该选项正确,符合题意.
故答案为:D.
【分析】A、根据合并同类项法则“把同类项的系数相加,字母和字母的指数不变”即可判断此选项;
B、由完全平方公式“(a-b)2=a2-2ab+b2”即可判断此选项;
C、根据积的乘方法则“把积中的每一个因式分别乘方,再把所得的幂相乘”即可判断此选项;
D、根据单项式乘以单项式法则"单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式"即可判断此选项.
3.【答案】C
【解析】【解答】解:A、x2 x4=x6,故本选项错误;
B、3x与2y不是同类项,不能合并,故本选项错误;
C、(﹣x3)2=x6,故本选项正确;
D、y3÷y3=1,故本选项错误.
故选C.
【分析】分别根据同底数幂的乘法与除法、幂的乘方与积的乘方、合并同类项的法则对各选项进行逐一计算即可.
4.【答案】B
【解析】【解答】A、2a 3a=6a2,故不符合题意;
B、(3a2)3=27a6,故符合题意;
C、a4÷a2=a2,故不符合题意;
D、(a+b)2=a2+2ab+b2,故不符合题意;
故答案为:B.
【分析】(1)由同底数幂相乘,底数不变,指数相加可得原式=6a2;
(2)由积的乘方法则可得原式=27a6;
(3)由同底数幂相除,底数不变,指数相减可得原式=a2;
(4)由完全平方公式可得原式=a2+2ab+b2。
5.【答案】D
【解析】【解答】解: =1.
故选D.
【分析】根据零指数幂直接计算即可.
6.【答案】B
【解析】【解答】A、应为(ab)5=a5b5,不符合题意;
B、a8÷a2=a8﹣2=a6,符合题意;
C、应为(a2)3=a2×3=a6,不符合题意;
D、应为(a﹣b)2=a2﹣2ab+b2,不符合题意.
故答案为:B.
【分析】(1)根据积的乘方法则可得,=;
(2)根据同底数幂的除法法则可得,=;
(3)根据幂的乘方法则可得,=;
(4)根据完全平方公式可得,=-2ab+.
7.【答案】D
【解析】【解答】解:A、a5 a3=a8,故本选项不符合题意;
B、a3+a3=2a3,故本选项不符合题意;
C、(a3)2=a6,故本选项不符合题意;
D、a5÷a3=a2,故本选项符合题意;
故答案为:D.
【分析】根据同底数幂的乘法,底数不变,指数相加;同底数幂的除法,底数不变,指数相减;幂的乘方,底数不变,指数相乘.
8.【答案】B
【解析】【解答】A、m3 m2=m5,A不符合题意;
B、(m3)2=m6,B符合题意;
C、m12÷m2=m10,C不符合题意;
D、m6 m=m7,D不符合题意;
故答案为:B.
【分析】依据同底数幂的乘法法则可对A作出判断;依据幂的乘方法则可对B作出判断;依据同底数幂的除法法则可对C作出判断;依据同底数幂的乘法法则可对D作出判断.
9.【答案】C
【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】0.000 0025=2.5×10-6;
故选:C
【点评】本题考查了用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
10.【答案】D
【解析】【分析】本题直接求解难度较大,故采用代入法,间接验证.
【解答】∵1+2+3+…+k=k(k+1)
∴k(k+1)=n2,
当k=1时,则k(k+1)=1,n=1,显然成立.
当k=8时,则k(k+1)=36,此时n=6,成立;
当k=49时,则k(k+1)=25×49,n=35,成立.
故答案为D.
【点评】本题考查完全平方数.同学们对于做选择题目,采用将选项代入验证的方法,有时候起到事半功倍的效果,本题就是这样,如直接求解,难度非常大,这样求解简单多了
11.【答案】
【解析】【解答】解:数0.00035用科学记数法表示为 .
故答案为: .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数,据此解答即可.
12.【答案】8
【解析】【解答】解: ,
,
原式 .
故答案为:8.
【分析】直接利用幂的乘方运算法则的逆用与同底数幂的除法计算得出答案.
13.【答案】-24
【解析】【解答】解:∵x+y=4,x-y=-6,
∴x2-y2=(x+y)(x-y)=4×(-6)=-24.
故答案为:-24.
【分析】根据平方差公式可得x2-y2=(x+y)(x-y),然后将已知条件代入进行计算.
14.【答案】5
【解析】【解答】解:∵时,,
∴,
∴,
∴,
∴当时,,
故答案为:
【分析】先根据题意代入x=-3即可得到,进而代入x=3即可求解。
15.【答案】解:(1)a2+b2=(a+b)2-2ab=25+4=29;
(2)(a-b)2=(a+b)2-4ab=52-4×(-2)=25+8=33.
【解析】【分析】本题利用完全平方公式,
(1)只需将a+b=5平方,代入ab=-2,即可求得a2+b2的值.
(2)将a2+b2,ab的值代入计算即可.
16.【答案】(1)解:原式=2+2× -1-27
=2+0.5-28
=-25.5
(2)解:原式=
=
=1+4
=5
【解析】【分析】(1)考查负整数次幂的法则 (a不为0),及非零数的0次幂为1;(2)运用平方差公式,积的乘方的逆运算进行简便计算.
17.【答案】(1)a-b
(2)(a+b)2-4ab;(a-b)2
(3)解:∵(a-b)2与(a+b)2-4ab都表示阴影部分的面积,
∴(a-b)2=(a+b)2-4ab.
【解析】【解答】解:(1)图2中的阴影部分的正方形的边长等于a-b;
故答案为:a-b;
(2)方法一:S阴影=S正方形-4S长方形=(a+b)2-4ab;
方法二:∵分成的四块小长方形形状和大小都一样,
∴每一个小长方形的长为a,宽为b,
∴阴影部分的正方形的边长为(a-b),
∴S阴影=(a-b)2;
故答案为:(a+b)2-4ab;(a-b)2 ;
【分析】(1)观察图形阴影部分的正方形的边长等于小长方形的长减去宽,据此直接写出边长即可;
(2)根据阴影部分的面积=正方形的面积-4个小长方形的面积;根据正方形的面积=边长的平方进行求解即可;
(3)根据阴影部分图形的面积恒等即可得出结论.
18.【答案】(1)
(2)3
(3)解:
.
【解析】【解答】解:(1)依题意,左右两部分的面积可以表示为
故答案为:.
(2)∵,,
∴
故答案为:3.
【分析】(1)根据两部分的阴影部分面积相等,即可求解;
(2)根据平方差公式进行计算即可求解;
(3)每一项根据平方差公式进行计算,进而化简即可求解.
19.【答案】解:∵an=3,bm=5,
∴a3n+b2m
=(an)2+(bm)2
=32+52
=34
【解析】【分析】先根据幂的乘方变形,再代入求出即可.
20.【答案】(1)16;40
(2)解:32a 3b=32a÷33b
=(3a)2÷(3b)3
=42÷53
= .
【解析】【解答】解:(1)32a=(3a)2=42=16;3b+c=3b 3c=5×8=40;
【分析】(1)直接利用幂的乘方运算法则计算得出答案,直接利用同底数幂的乘法运算法则计算得出答案;(2)直接利用同底数幂的乘除运算法则进而计算得出答案.
21.【答案】(1)解:
,
所以,
即,
解之得.
(2)解:当,时,
.
【解析】【分析】(1)将b=6代入
计算可得
,再利用待定系数法可得
,,再求出a的值即可;
(2)将
,代入
,再利用多项式乘多项式的计算方法求解即可。
22.【答案】(1)解:活动场所面积: ,
花草的面积:(a+4a+5a)(1.5a+3a+1.5a) –[4a×3a+π( a)2]= ,
(2)解:(a+4a+5a)(1.5a+3a+1.5a)÷(3a×4a)= =5,
所以整座健身馆的面积是成年人活动场所面积的5倍.
【解析】【分析】(1)利用图形中的相关数据,列式计算求出活动场所的面积及花草的面积.
(2)利用整座健身馆的面积÷成年人活动场所面积,列式计算可求出结果.
23.【答案】(1)B
(2)解:∵
∴
∵
∴
∴ ;
(3)解:
【解析】【解答】(1)根据阴影部分的面积可得
故上述操作能验证的等式是B;
【分析】(1)结合图1和图2阴影部分面积建立等式即可;(2)利用平方差公式计算即可;(3)利用平方差公式展开计算化简,最后求值即可。
1 / 1
一、单选题
1.a6÷a2的结果是( )
A.a3 B.a4 C.a8 D.a12
2.下列计算正确的是( )
A.x2+x2=x4 B.(x﹣y)2=x2﹣y2
C.(x2y)3=x6y D.(﹣x)2x3=x5
3.下列运算正确的是( )
A.x2 x4=x8 B.3x+2y=6xy
C.(﹣x3)2=x6 D.y3÷y3=y
4.下列各运算中,计算正确的是( )
A.2a 3a=6a B.(3a2)3=27a6
C.a4÷a2=2a D.(a+b)2=a2+ab+b2
5.计算 的结果是( )
A.﹣1 B. C.0 D.1
6.下列运算正确的是( )
A.(ab)5=ab5 B.a8÷a2=a6
C.(a2)3=a5 D.(a﹣b)2=a2﹣b2
7. 下列计算正确的是( )
A.a5 a3=2a8 B.a3+a3=a6 C.(a3)2=a5 D.a5÷a3=a2
8.下面计算结果等于m6的是( )
A.m3 m2 B.(m3)2 C.m12÷m2 D.m6 m
9.PM 2.5是指大气中直径小于或等于0.0000025 m的颗粒物,将0.0000025用科学记数法表示为( )
A.0.25×10-5 B.0.25×10-6 C.2.5×10-6 D.2.5×10-5
10.若1+2+3+…+k之和为一完全平方n2,若n小于100,则k可能的值为( )
A.8 B.1,8 C.8,49 D.1,8,49.
二、填空题
11.数0.00035用科学记数法表示为 .
12.已知 ,则 .
13.已知,则 .
14. 已知当x=﹣3时,ax3﹣bx+5=9,则x=3时,ax3﹣bx+9的值为 .
三、解答题
15.a+b=5,ab=-2,求:和的值.
16.计算:
(1)( )﹣1+2×(﹣2)﹣2-(﹣π+3.14)0﹣( )﹣3
(2)用简便方法计算:1252﹣124×126﹣4101×(﹣0.25)99.
17.如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按.如图2的形状拼成一个正方形.
(1)图2的阴影部分的正方形的边长是 .
(2)用两种不同的方法求图中阴影部分的面积.
【方法1】= ;
【方法2】= ;
(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
18.如图,边长为的大正方形有一个边长为的小正方形,把图中的阴影部分拼成一个长方形如图所示
(1)观察左、右两图的阴影部分面积,可以得到公式 ;
(2)已知,,则 ;
(3)请应用这个公式完成下列计算:.
19.若an=3,bm=5,求a3n+b2m的值.
四、综合题
20.已知3a=4,3b=5,3c=8.
(1)填空:32a= ;3b+c的值为 ;
(2)求32a﹣3b的值.
21.在计算时,甲把错看成了6,得到结果是:,
(1)求出a的值;
(2)在(1)的条件下,且时,计算的结果.
22.某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.
(1)活动场所和花草的面积各是多少;
(2)整座健身馆的面积是成年人活动场所面积的多少倍.
23.从边长为 a 的正方形剪掉一个边长为 b 的正方形(如图 1),然后将剩余部分拼成一个长方形(如图 2).
(1)上述操作能验证的等式是_______(请选择正确的一个)
A.a2﹣2ab+b2 =(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2 +ab=a(a+b)
(2)若 x2 ﹣9y2=12,x+3y=4,求 x﹣3y 的值;
(3)计算: .
答案解析部分
1.【答案】B
【解析】【解答】解:,
故答案为:B.
【分析】利用同底数幂的除法的计算法则求解即可。
2.【答案】D
【解析】【解答】解:A、x2+x2=2x2,故该选项不正确,不符合题意;
B、 (x﹣y)2=x2-2xy+y2,故该选项不正确,不符合题意;
C、(x2y)3=x6y3,故该选项不正确,不符合题意;
D、 (﹣x)2x3=x5故该选项正确,符合题意.
故答案为:D.
【分析】A、根据合并同类项法则“把同类项的系数相加,字母和字母的指数不变”即可判断此选项;
B、由完全平方公式“(a-b)2=a2-2ab+b2”即可判断此选项;
C、根据积的乘方法则“把积中的每一个因式分别乘方,再把所得的幂相乘”即可判断此选项;
D、根据单项式乘以单项式法则"单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式"即可判断此选项.
3.【答案】C
【解析】【解答】解:A、x2 x4=x6,故本选项错误;
B、3x与2y不是同类项,不能合并,故本选项错误;
C、(﹣x3)2=x6,故本选项正确;
D、y3÷y3=1,故本选项错误.
故选C.
【分析】分别根据同底数幂的乘法与除法、幂的乘方与积的乘方、合并同类项的法则对各选项进行逐一计算即可.
4.【答案】B
【解析】【解答】A、2a 3a=6a2,故不符合题意;
B、(3a2)3=27a6,故符合题意;
C、a4÷a2=a2,故不符合题意;
D、(a+b)2=a2+2ab+b2,故不符合题意;
故答案为:B.
【分析】(1)由同底数幂相乘,底数不变,指数相加可得原式=6a2;
(2)由积的乘方法则可得原式=27a6;
(3)由同底数幂相除,底数不变,指数相减可得原式=a2;
(4)由完全平方公式可得原式=a2+2ab+b2。
5.【答案】D
【解析】【解答】解: =1.
故选D.
【分析】根据零指数幂直接计算即可.
6.【答案】B
【解析】【解答】A、应为(ab)5=a5b5,不符合题意;
B、a8÷a2=a8﹣2=a6,符合题意;
C、应为(a2)3=a2×3=a6,不符合题意;
D、应为(a﹣b)2=a2﹣2ab+b2,不符合题意.
故答案为:B.
【分析】(1)根据积的乘方法则可得,=;
(2)根据同底数幂的除法法则可得,=;
(3)根据幂的乘方法则可得,=;
(4)根据完全平方公式可得,=-2ab+.
7.【答案】D
【解析】【解答】解:A、a5 a3=a8,故本选项不符合题意;
B、a3+a3=2a3,故本选项不符合题意;
C、(a3)2=a6,故本选项不符合题意;
D、a5÷a3=a2,故本选项符合题意;
故答案为:D.
【分析】根据同底数幂的乘法,底数不变,指数相加;同底数幂的除法,底数不变,指数相减;幂的乘方,底数不变,指数相乘.
8.【答案】B
【解析】【解答】A、m3 m2=m5,A不符合题意;
B、(m3)2=m6,B符合题意;
C、m12÷m2=m10,C不符合题意;
D、m6 m=m7,D不符合题意;
故答案为:B.
【分析】依据同底数幂的乘法法则可对A作出判断;依据幂的乘方法则可对B作出判断;依据同底数幂的除法法则可对C作出判断;依据同底数幂的乘法法则可对D作出判断.
9.【答案】C
【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】0.000 0025=2.5×10-6;
故选:C
【点评】本题考查了用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
10.【答案】D
【解析】【分析】本题直接求解难度较大,故采用代入法,间接验证.
【解答】∵1+2+3+…+k=k(k+1)
∴k(k+1)=n2,
当k=1时,则k(k+1)=1,n=1,显然成立.
当k=8时,则k(k+1)=36,此时n=6,成立;
当k=49时,则k(k+1)=25×49,n=35,成立.
故答案为D.
【点评】本题考查完全平方数.同学们对于做选择题目,采用将选项代入验证的方法,有时候起到事半功倍的效果,本题就是这样,如直接求解,难度非常大,这样求解简单多了
11.【答案】
【解析】【解答】解:数0.00035用科学记数法表示为 .
故答案为: .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数,据此解答即可.
12.【答案】8
【解析】【解答】解: ,
,
原式 .
故答案为:8.
【分析】直接利用幂的乘方运算法则的逆用与同底数幂的除法计算得出答案.
13.【答案】-24
【解析】【解答】解:∵x+y=4,x-y=-6,
∴x2-y2=(x+y)(x-y)=4×(-6)=-24.
故答案为:-24.
【分析】根据平方差公式可得x2-y2=(x+y)(x-y),然后将已知条件代入进行计算.
14.【答案】5
【解析】【解答】解:∵时,,
∴,
∴,
∴,
∴当时,,
故答案为:
【分析】先根据题意代入x=-3即可得到,进而代入x=3即可求解。
15.【答案】解:(1)a2+b2=(a+b)2-2ab=25+4=29;
(2)(a-b)2=(a+b)2-4ab=52-4×(-2)=25+8=33.
【解析】【分析】本题利用完全平方公式,
(1)只需将a+b=5平方,代入ab=-2,即可求得a2+b2的值.
(2)将a2+b2,ab的值代入计算即可.
16.【答案】(1)解:原式=2+2× -1-27
=2+0.5-28
=-25.5
(2)解:原式=
=
=1+4
=5
【解析】【分析】(1)考查负整数次幂的法则 (a不为0),及非零数的0次幂为1;(2)运用平方差公式,积的乘方的逆运算进行简便计算.
17.【答案】(1)a-b
(2)(a+b)2-4ab;(a-b)2
(3)解:∵(a-b)2与(a+b)2-4ab都表示阴影部分的面积,
∴(a-b)2=(a+b)2-4ab.
【解析】【解答】解:(1)图2中的阴影部分的正方形的边长等于a-b;
故答案为:a-b;
(2)方法一:S阴影=S正方形-4S长方形=(a+b)2-4ab;
方法二:∵分成的四块小长方形形状和大小都一样,
∴每一个小长方形的长为a,宽为b,
∴阴影部分的正方形的边长为(a-b),
∴S阴影=(a-b)2;
故答案为:(a+b)2-4ab;(a-b)2 ;
【分析】(1)观察图形阴影部分的正方形的边长等于小长方形的长减去宽,据此直接写出边长即可;
(2)根据阴影部分的面积=正方形的面积-4个小长方形的面积;根据正方形的面积=边长的平方进行求解即可;
(3)根据阴影部分图形的面积恒等即可得出结论.
18.【答案】(1)
(2)3
(3)解:
.
【解析】【解答】解:(1)依题意,左右两部分的面积可以表示为
故答案为:.
(2)∵,,
∴
故答案为:3.
【分析】(1)根据两部分的阴影部分面积相等,即可求解;
(2)根据平方差公式进行计算即可求解;
(3)每一项根据平方差公式进行计算,进而化简即可求解.
19.【答案】解:∵an=3,bm=5,
∴a3n+b2m
=(an)2+(bm)2
=32+52
=34
【解析】【分析】先根据幂的乘方变形,再代入求出即可.
20.【答案】(1)16;40
(2)解:32a 3b=32a÷33b
=(3a)2÷(3b)3
=42÷53
= .
【解析】【解答】解:(1)32a=(3a)2=42=16;3b+c=3b 3c=5×8=40;
【分析】(1)直接利用幂的乘方运算法则计算得出答案,直接利用同底数幂的乘法运算法则计算得出答案;(2)直接利用同底数幂的乘除运算法则进而计算得出答案.
21.【答案】(1)解:
,
所以,
即,
解之得.
(2)解:当,时,
.
【解析】【分析】(1)将b=6代入
计算可得
,再利用待定系数法可得
,,再求出a的值即可;
(2)将
,代入
,再利用多项式乘多项式的计算方法求解即可。
22.【答案】(1)解:活动场所面积: ,
花草的面积:(a+4a+5a)(1.5a+3a+1.5a) –[4a×3a+π( a)2]= ,
(2)解:(a+4a+5a)(1.5a+3a+1.5a)÷(3a×4a)= =5,
所以整座健身馆的面积是成年人活动场所面积的5倍.
【解析】【分析】(1)利用图形中的相关数据,列式计算求出活动场所的面积及花草的面积.
(2)利用整座健身馆的面积÷成年人活动场所面积,列式计算可求出结果.
23.【答案】(1)B
(2)解:∵
∴
∵
∴
∴ ;
(3)解:
【解析】【解答】(1)根据阴影部分的面积可得
故上述操作能验证的等式是B;
【分析】(1)结合图1和图2阴影部分面积建立等式即可;(2)利用平方差公式计算即可;(3)利用平方差公式展开计算化简,最后求值即可。
1 / 1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
