粤教版2019必修第一册高一物理同步精品练习2.5匀变速直线运动与汽车安全行驶(作业)(第2课时)(追及相遇问题)(原卷版+解析)
文档属性
| 名称 | 粤教版2019必修第一册高一物理同步精品练习2.5匀变速直线运动与汽车安全行驶(作业)(第2课时)(追及相遇问题)(原卷版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 578.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
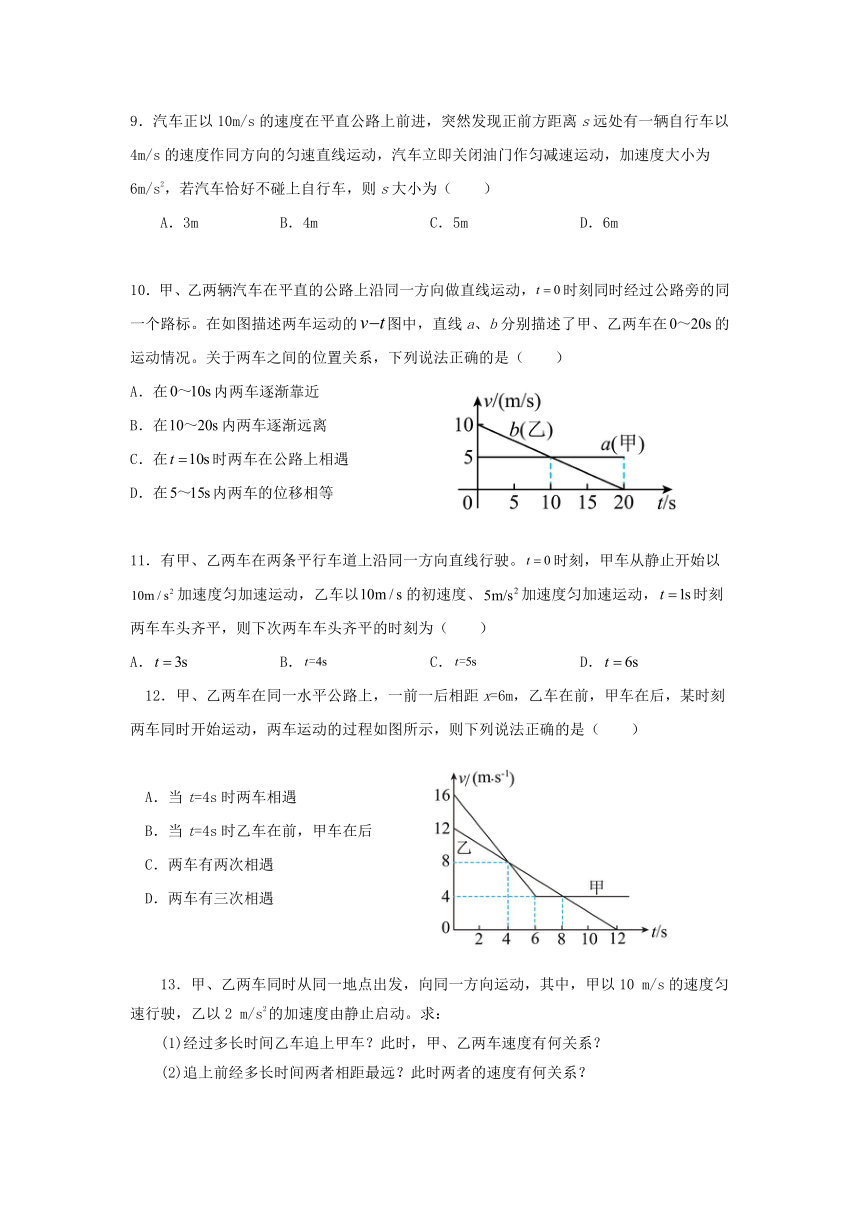
| 科目 | 物理 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览



文档简介
2.5 匀变速直线运动与汽车安全行驶
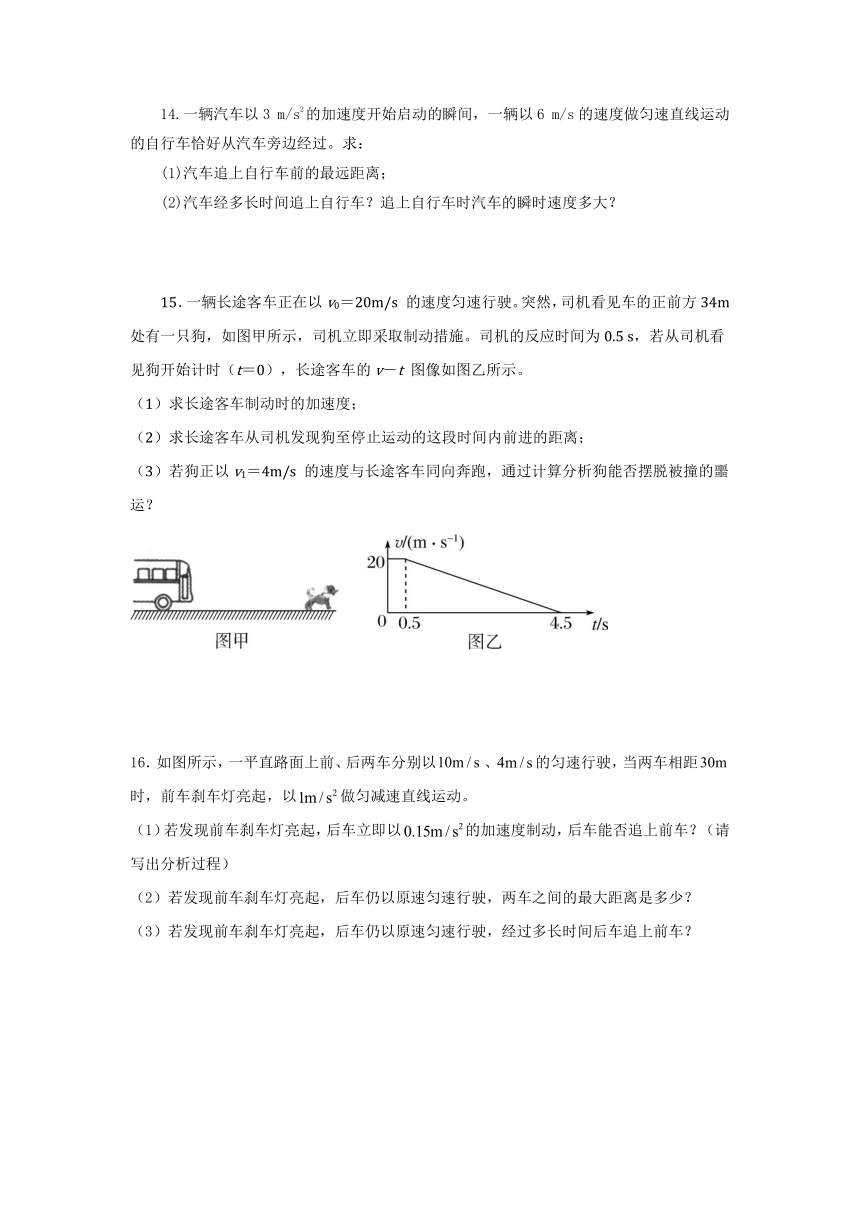
追及相遇问题 (原卷版)
1.(多选)如图所示是做直线运动的甲、乙两物体的位移—时间图像,由图像可知( )
A.甲起动的时间比乙晚t1秒
B.当t=t2时两物体相遇
C.当t=t2时两物体相距最远
D.当t=t3时两物体相距s0米
2.(多选)如图所示,计时开始时A、B两质点在同一位置,由图可知( )
A.A、B两质点运动方向相反
B.2 s末A、B两质点相遇
C.2 s末A、B两质点速度大小相等,方向相同
D.A、B两质点速度相同时,相距6 m
3.(多选)两物体在同一直线上,同时由同一位置向同一方向运动,其速度图像如图所示,下列说法中正确的是( )
A.开始阶段B跑在A的前面,20 s后B落在A后面
B.20 s末B追上A,且A、B速度相等
C.40 s末A追上B
D.在A追B之间的20 s末,两物体相距最远
4.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标。在描述两车运动的v-t图中(如图所示),直线a、b分别描述了甲、乙两车在0~20 s的运动情况。关于两车之间的位置关系,下列说法正确的是( )
A.在0~10 s内两车逐渐靠近
B.在10~20 s内两车逐渐远离
C.在5~15 s内两车的位移相等
D.在t=10 s时两车在公路上相遇
5.甲车静止在一平直公路上,乙车以大小为6m/s的速度做匀速直线运动从甲车旁经过,甲车立即做初速为零的匀加速直线运动,经过4s恰好追上乙车,不考虑车辆尺寸,则( )
A.追上乙车时,甲车的速度大小为6m/s
B.追上乙车时,甲车的速度大小为24m/s
C.甲车匀加速直线运动的加速度大小为1m/s2
D.甲车匀加速直线运动的加速度大小为3m/s2
6.甲、乙两辆汽车沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动状况的描述正确的是( )
A.在第末,乙车改变运动方向
B.在第末,甲、乙两车可能相距
C.在第末,甲、乙两车一定相遇
D.两车不可能相遇两次
7.两辆完全相同的汽车,沿平直公路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车。已知前车在刹车过程中前行的距离为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为( )
A.s B.2s
C.3s D.4s
8.甲、乙两名运动员在泳池里训练,时刻从泳池的两端出发,甲、乙的速度-时间图象分别如图1、2所示,若不计转向的时间且持续运动,两运动员均可视为质点。下列说法正确的是( )
A.游泳池长
B.两运动员一定不会在泳池的两端相遇
C.从时刻起经过两运动员共相遇了3次
D.在内,两运动员的平均速度大小之比为
9.汽车正以10m/s的速度在平直公路上前进,突然发现正前方距离s远处有一辆自行车以4m/s的速度作同方向的匀速直线运动,汽车立即关闭油门作匀减速运动,加速度大小为6m/s2,若汽车恰好不碰上自行车,则s大小为( )
A.3m B.4m C.5m D.6m
10.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,时刻同时经过公路旁的同一个路标。在如图描述两车运动的图中,直线a、b分别描述了甲、乙两车在的运动情况。关于两车之间的位置关系,下列说法正确的是( )
A.在内两车逐渐靠近
B.在内两车逐渐远离
C.在时两车在公路上相遇
D.在内两车的位移相等
11.有甲、乙两车在两条平行车道上沿同一方向直线行驶。时刻,甲车从静止开始以加速度匀加速运动,乙车以的初速度、加速度匀加速运动,时刻两车车头齐平,则下次两车车头齐平的时刻为( )
A. B. C. D.
12.甲、乙两车在同一水平公路上,一前一后相距x=6m,乙车在前,甲车在后,某时刻两车同时开始运动,两车运动的过程如图所示,则下列说法正确的是( )
A.当t=4s时两车相遇
B.当t=4s时乙车在前,甲车在后
C.两车有两次相遇
D.两车有三次相遇
13.甲、乙两车同时从同一地点出发,向同一方向运动,其中,甲以10 m/s的速度匀速行驶,乙以2 m/s2的加速度由静止启动。求:
(1)经过多长时间乙车追上甲车?此时,甲、乙两车速度有何关系?
(2)追上前经多长时间两者相距最远?此时两者的速度有何关系?
14.一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车旁边经过。求:
(1)汽车追上自行车前的最远距离;
(2)汽车经多长时间追上自行车?追上自行车时汽车的瞬时速度多大?
15.一辆长途客车正在以v0=20m/s 的速度匀速行驶。突然,司机看见车的正前方34m 处有一只狗,如图甲所示,司机立即采取制动措施。司机的反应时间为0.5 s,若从司机看见狗开始计时(t=0),长途客车的v-t 图像如图乙所示。
(1)求长途客车制动时的加速度;
(2)求长途客车从司机发现狗至停止运动的这段时间内前进的距离;
(3)若狗正以v1=4m/s 的速度与长途客车同向奔跑,通过计算分析狗能否摆脱被撞的噩运?
16.如图所示,一平直路面上前、后两车分别以、的匀速行驶,当两车相距时,前车刹车灯亮起,以做匀减速直线运动。
(1)若发现前车刹车灯亮起,后车立即以的加速度制动,后车能否追上前车?(请写出分析过程)
(2)若发现前车刹车灯亮起,后车仍以原速匀速行驶,两车之间的最大距离是多少?
(3)若发现前车刹车灯亮起,后车仍以原速匀速行驶,经过多长时间后车追上前车?
2.5 匀变速直线运动与汽车安全行驶
追及相遇问题 (解析版)
1.(多选)如图所示是做直线运动的甲、乙两物体的位移—时间图像,由图像可知( )
A.甲起动的时间比乙晚t1秒
B.当t=t2时两物体相遇
C.当t=t2时两物体相距最远
D.当t=t3时两物体相距s0米
【答案】BD
【解析】由甲、乙两物体位移—时间图像可知,乙比甲晚运动t1秒,t2时刻位移相等,甲、乙相遇。t3时刻s甲=0,s乙=s0,两物体相距s0,A、C错误,B、D正确。
2.(多选)如图所示,计时开始时A、B两质点在同一位置,由图可知( )
A.A、B两质点运动方向相反
B.2 s末A、B两质点相遇
C.2 s末A、B两质点速度大小相等,方向相同
D.A、B两质点速度相同时,相距6 m
【答案】CD
【解析】A质点做匀减速直线运动,B质点做初速度为零的匀加速直线运动。两质点从同一出发点,同时向同一方向运动。交点表示两质点在2 s这一时刻有相同的速度。这时两质点间有最大距离,因质点的位移对应于图线与坐标及坐标轴所围成的面积,故这最大距离s可由对应于质点A位移的梯形面积与对应于质点B位移的三角形面积之差来求。即
s=s1-s2= m-×2×2 m=6 m
应了解速度图线不同于位移图线,位移图线相交表示在同一位置,而速度图线相交则表示速度相同。
3.(多选)两物体在同一直线上,同时由同一位置向同一方向运动,其速度图像如图所示,下列说法中正确的是( )
A.开始阶段B跑在A的前面,20 s后B落在A后面
B.20 s末B追上A,且A、B速度相等
C.40 s末A追上B
D.在A追B之间的20 s末,两物体相距最远
【答案】CD
【解析】图线所围的面积大小表示物体运动的位移,从图中可知40 s时,两物体相遇,之前B一直在A前面,故选项C正确,当A、B速度相同时相距最远,故选项D正确。
4.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标。在描述两车运动的v-t图中(如图所示),直线a、b分别描述了甲、乙两车在0~20 s的运动情况。关于两车之间的位置关系,下列说法正确的是( )
A.在0~10 s内两车逐渐靠近
B.在10~20 s内两车逐渐远离
C.在5~15 s内两车的位移相等
D.在t=10 s时两车在公路上相遇
【答案】C
【解析】由v-t图像可知,0~10 s内,v乙>v甲,两车逐渐远离,10~20 s内,v乙<v甲,两车逐渐靠近,故选项A、B均错;
v-t图线与时间轴所围的面积的数值表示位移,5~15 s内,两图线与t轴包围的面积相等,故两车的位移相等,选项C对;t=20 s时,两车的位移再次相等,说明两车再次相遇,故D错。
5.甲车静止在一平直公路上,乙车以大小为6m/s的速度做匀速直线运动从甲车旁经过,甲车立即做初速为零的匀加速直线运动,经过4s恰好追上乙车,不考虑车辆尺寸,则( )
A.追上乙车时,甲车的速度大小为6m/s
B.追上乙车时,甲车的速度大小为24m/s
C.甲车匀加速直线运动的加速度大小为1m/s2
D.甲车匀加速直线运动的加速度大小为3m/s2
【答案】D
【解析】CD.甲乙两车位移相等,有
解得甲车匀加速直线运动的加速度大小为
a=3m/s2
选项C错误,D正确;
AB.追上乙车时,由
甲车的速度大小12m/s,选项AB错误。
故选D。
6.甲、乙两辆汽车沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动状况的描述正确的是( )
A.在第末,乙车改变运动方向
B.在第末,甲、乙两车可能相距
C.在第末,甲、乙两车一定相遇
D.两车不可能相遇两次
【答案】B
【解析】A.乙车在10内朝正方向做匀减速直线运动,10s后朝正方向做匀加速直线运动,故在第末,乙车没有改变运动方向,A错误;
BC.题中未指明甲、乙两车出发位置的关系,故在第末,甲、乙两车可能相距,在第末,甲、乙两车可能相遇,也可能不相遇,B正确,C错误;
D.若开始时甲在乙后方,甲先超过乙一次,然后乙速度逐渐增大,再超过甲一次,故两车可能相遇两次,D错误。
故选B。
7.两辆完全相同的汽车,沿平直公路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车。已知前车在刹车过程中前行的距离为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为( )
A.s B.2s
C.3s D.4s
【答案】B
【解析】依题意可画出两车的速度图像如图所示。图线Ⅰ表示前车以恒定加速度刹车时的运动情况,在它刹车时后车以图线Ⅱ继续前进,当前车停止时,后车开始以相同的加速度刹车,如图线Ⅲ(Ⅲ与Ⅰ平行),前车刹车经过的位移为△AOB的“面积”,其大小为s,要保证两车不相撞,两车在匀速行驶时保持的距离s′至少为 ABDC的“面积”,它等于△AOB“面积”的2倍,即s′=2 s。答案选B。
8.甲、乙两名运动员在泳池里训练,时刻从泳池的两端出发,甲、乙的速度-时间图象分别如图1、2所示,若不计转向的时间且持续运动,两运动员均可视为质点。下列说法正确的是( )
A.游泳池长
B.两运动员一定不会在泳池的两端相遇
C.从时刻起经过两运动员共相遇了3次
D.在内,两运动员的平均速度大小之比为
【答案】C
【解析】
A.根据图线与坐标轴围成的图形面积表示位移,可知游泳池长度
或者
故A错误;
B.如图所示
由甲、乙的位移-时间图线的交点表示相遇可知,甲、乙在时在泳池的一端相遇,故B错误;
C.在内甲、乙相遇3次,故C正确;
D.在内,甲的位移大小为
乙的位移大小为
在内两运动员的平均速度大小之比为
故D错误。
故选C。
9.汽车正以10m/s的速度在平直公路上前进,突然发现正前方距离s远处有一辆自行车以4m/s的速度作同方向的匀速直线运动,汽车立即关闭油门作匀减速运动,加速度大小为6m/s2,若汽车恰好不碰上自行车,则s大小为( )
A.3m B.4m C.5m D.6m
【答案】A
【解析】
当两者速度相等时,相距最近,有
v1+at=v2
解得
t=1s
此时汽车前进的距离为
自行车前进的距离为
若汽车恰好不碰上自行车,则s的大小为
故选A。
10.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,时刻同时经过公路旁的同一个路标。在如图描述两车运动的图中,直线a、b分别描述了甲、乙两车在的运动情况。关于两车之间的位置关系,下列说法正确的是( )
A.在内两车逐渐靠近
B.在内两车逐渐远离
C.在时两车在公路上相遇
D.在内两车的位移相等
【答案】D
【解析】
A.在秒内,乙车在甲的前方,而且乙的速度大于甲的速度,则两车逐渐远离,A错误;
B.在秒内,乙车在甲的前方,乙的速度小于甲的速度,则两车逐渐靠近,B错误;
C.根据图象的“面积”等于物体的位移大小,可以看出,在秒时乙车的位移大于甲车的位移,时刻又在同一位置出发,所以在秒时两车没有相遇,C错误;
D.在秒内两车图线的“面积”相等,则通过的位移相等,D正确。
故选D。
11.有甲、乙两车在两条平行车道上沿同一方向直线行驶。时刻,甲车从静止开始以加速度匀加速运动,乙车以的初速度、加速度匀加速运动,时刻两车车头齐平,则下次两车车头齐平的时刻为( )
A. B. C. D.
【答案】A
【解析】
内,甲和乙的位移为
故有
说明时刻甲在乙的前方,设下次车头齐平的时刻为t,
化简得
解得
或
故选A。
12.甲、乙两车在同一水平公路上,一前一后相距x=6m,乙车在前,甲车在后,某时刻两车同时开始运动,两车运动的过程如图所示,则下列说法正确的是( )
A.当t=4s时两车相遇
B.当t=4s时乙车在前,甲车在后
C.两车有两次相遇
D.两车有三次相遇
【答案】D
【解析】
AB.速度图线与时间轴围成的面积表示位移,则知当t=4s时,甲的位移大于乙的位移,0-4s,甲的位移为
x甲=×(16+8)×4m=48m
乙的位移为
x乙=×(12+8)×4m=40m
位移之差
Δx=x甲-x乙=8m
开始时,甲、乙两车在同一水平道路上,一前一后相距x=6m,由此可知,t=4s时,甲车在前,乙车在后,相距2m,故AB错误;
CD.t=4s时,甲车在前,乙车在后,所以两车第一次相遇发生在4s之前;当t=6s时,甲的位移为
x′甲=×(16+4)×6m=60m
乙的位移为
x′乙=×(12+6)×6m=54m
位移之差等于6m,而两车是从开始出发时,甲、乙两车在同一水平道路上,一前一后相距x=6m,所以当t=6s时两车第二次相遇;t=6s后,由于乙的速度大于甲的速度,乙又跑到前面,8s后,由于甲的速度大于乙的速度,两车还会发生第三次相遇,故C错误,D正确。
故选D。
13.甲、乙两车同时从同一地点出发,向同一方向运动,其中,甲以10 m/s的速度匀速行驶,乙以2 m/s2的加速度由静止启动。求:
(1)经过多长时间乙车追上甲车?此时,甲、乙两车速度有何关系?
(2)追上前经多长时间两者相距最远?此时两者的速度有何关系?
【答案】
【解析】
(1)设追上所用时间为t
由s甲=s乙得v甲t=a乙t2
10t=×2×t2
t=10 s
此时v乙=a乙t=2×10 m/s=20 m/s=2v甲
(2)相距最远时满足v乙=v甲=10 m/s
解得时间t′== s=5 s。
答案:(1)10 s v乙=2v甲 (2)5 s v乙=v甲
14.一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车旁边经过。求:
(1)汽车追上自行车前的最远距离;
(2)汽车经多长时间追上自行车?追上自行车时汽车的瞬时速度多大?
【答案】(1)6 m (2)4 s 12 m/s
【解析】本题考查追及问题的求解,关键是找到达到最大距离的临界条件。
法一:物理分析的方法
(1)汽车“追赶”自行车,它们的间距先增后减,当二者速度相同时,间距最大。设二者速度相同,均为6 m/s,所经过的时间为t1,则at1=v自,t1== s=2 s。最大间距Δs=v自t1-at12=(6×2-×3×22) m=6 m。
(2)汽车追上自行车所用时间为t2,则v自t2=at22,即6t2=×3×t22,t2=4 s,此时汽车速度v2=at2=12 m/s。
法二:数学的方法
(1)经过时间t,二者间距为
Δs=v自t-at2=6t-×3×t2=-(t-2)2+6,
当t=2 s时,间距最大,Δsm=6 m。
(2)追上时解法同法一。
法三:图像法
根据题意,从汽车启动瞬间计时,分别作出汽车与自行车的v-t图像,如图所示:
(1)由图像可知,2 s前自行车与汽车间距增大,2 s后汽车“追赶”自行车,它们的间距减小,因此2 s末时刻二者间距最大,最大距离与三角形OAB面积数值相等,即Δsm=6×2× m=6 m。
(2)当所画阴影三角形OAB与三角形CDB面积相等时汽车追上自行车,由两三角形全等可知,在t=4 s时追上自行车,由图像知此时汽车速度为12 m/s。
15.一辆长途客车正在以v0=20m/s 的速度匀速行驶。突然,司机看见车的正前方34m 处有一只狗,如图甲所示,司机立即采取制动措施。司机的反应时间为0.5 s,若从司机看见狗开始计时(t=0),长途客车的v-t 图像如图乙所示。
(1)求长途客车制动时的加速度;
(2)求长途客车从司机发现狗至停止运动的这段时间内前进的距离;
(3)若狗正以v1=4m/s 的速度与长途客车同向奔跑,通过计算分析狗能否摆脱被撞的噩运?
【答案】(1);(2)50m;(3)狗能摆脱被撞的噩运
【解析】
(1)根据图像可得
(2)速度图象与时间轴围成的面积等于物体通过的位移,则有
(3)当客车速度减为与狗的速度相同时,所需时间为
司机从看到狗到速度减为与狗速度相同时,通过位移为
则有
所以狗不会被撞。
16.如图所示,一平直路面上前、后两车分别以、的匀速行驶,当两车相距时,前车刹车灯亮起,以做匀减速直线运动。
(1)若发现前车刹车灯亮起,后车立即以的加速度制动,后车能否追上前车?(请写出分析过程)
(2)若发现前车刹车灯亮起,后车仍以原速匀速行驶,两车之间的最大距离是多少?
(3)若发现前车刹车灯亮起,后车仍以原速匀速行驶,经过多长时间后车追上前车?
【答案】(1)不能;(2);(3)
【解析】
(1)设后车为A,前车为B,A车刹车减速至0时刚好追上B车,则有
代入数据得
因为,故不能追上前车;
(2)当前、后两车速度相等时,相距最远,根据速度关系得
代入数据解得
此时,根据位移公式得
。
代入数据解得
(3)B车从刹车到停止运动所用时间
所发生位移
此时
则
可见此时A车并未追上B车,而是在B车停止后才追上,之后A车运动时间为
故所求时间为
追及相遇问题 (原卷版)
1.(多选)如图所示是做直线运动的甲、乙两物体的位移—时间图像,由图像可知( )
A.甲起动的时间比乙晚t1秒
B.当t=t2时两物体相遇
C.当t=t2时两物体相距最远
D.当t=t3时两物体相距s0米
2.(多选)如图所示,计时开始时A、B两质点在同一位置,由图可知( )
A.A、B两质点运动方向相反
B.2 s末A、B两质点相遇
C.2 s末A、B两质点速度大小相等,方向相同
D.A、B两质点速度相同时,相距6 m
3.(多选)两物体在同一直线上,同时由同一位置向同一方向运动,其速度图像如图所示,下列说法中正确的是( )
A.开始阶段B跑在A的前面,20 s后B落在A后面
B.20 s末B追上A,且A、B速度相等
C.40 s末A追上B
D.在A追B之间的20 s末,两物体相距最远
4.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标。在描述两车运动的v-t图中(如图所示),直线a、b分别描述了甲、乙两车在0~20 s的运动情况。关于两车之间的位置关系,下列说法正确的是( )
A.在0~10 s内两车逐渐靠近
B.在10~20 s内两车逐渐远离
C.在5~15 s内两车的位移相等
D.在t=10 s时两车在公路上相遇
5.甲车静止在一平直公路上,乙车以大小为6m/s的速度做匀速直线运动从甲车旁经过,甲车立即做初速为零的匀加速直线运动,经过4s恰好追上乙车,不考虑车辆尺寸,则( )
A.追上乙车时,甲车的速度大小为6m/s
B.追上乙车时,甲车的速度大小为24m/s
C.甲车匀加速直线运动的加速度大小为1m/s2
D.甲车匀加速直线运动的加速度大小为3m/s2
6.甲、乙两辆汽车沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动状况的描述正确的是( )
A.在第末,乙车改变运动方向
B.在第末,甲、乙两车可能相距
C.在第末,甲、乙两车一定相遇
D.两车不可能相遇两次
7.两辆完全相同的汽车,沿平直公路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车。已知前车在刹车过程中前行的距离为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为( )
A.s B.2s
C.3s D.4s
8.甲、乙两名运动员在泳池里训练,时刻从泳池的两端出发,甲、乙的速度-时间图象分别如图1、2所示,若不计转向的时间且持续运动,两运动员均可视为质点。下列说法正确的是( )
A.游泳池长
B.两运动员一定不会在泳池的两端相遇
C.从时刻起经过两运动员共相遇了3次
D.在内,两运动员的平均速度大小之比为
9.汽车正以10m/s的速度在平直公路上前进,突然发现正前方距离s远处有一辆自行车以4m/s的速度作同方向的匀速直线运动,汽车立即关闭油门作匀减速运动,加速度大小为6m/s2,若汽车恰好不碰上自行车,则s大小为( )
A.3m B.4m C.5m D.6m
10.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,时刻同时经过公路旁的同一个路标。在如图描述两车运动的图中,直线a、b分别描述了甲、乙两车在的运动情况。关于两车之间的位置关系,下列说法正确的是( )
A.在内两车逐渐靠近
B.在内两车逐渐远离
C.在时两车在公路上相遇
D.在内两车的位移相等
11.有甲、乙两车在两条平行车道上沿同一方向直线行驶。时刻,甲车从静止开始以加速度匀加速运动,乙车以的初速度、加速度匀加速运动,时刻两车车头齐平,则下次两车车头齐平的时刻为( )
A. B. C. D.
12.甲、乙两车在同一水平公路上,一前一后相距x=6m,乙车在前,甲车在后,某时刻两车同时开始运动,两车运动的过程如图所示,则下列说法正确的是( )
A.当t=4s时两车相遇
B.当t=4s时乙车在前,甲车在后
C.两车有两次相遇
D.两车有三次相遇
13.甲、乙两车同时从同一地点出发,向同一方向运动,其中,甲以10 m/s的速度匀速行驶,乙以2 m/s2的加速度由静止启动。求:
(1)经过多长时间乙车追上甲车?此时,甲、乙两车速度有何关系?
(2)追上前经多长时间两者相距最远?此时两者的速度有何关系?
14.一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车旁边经过。求:
(1)汽车追上自行车前的最远距离;
(2)汽车经多长时间追上自行车?追上自行车时汽车的瞬时速度多大?
15.一辆长途客车正在以v0=20m/s 的速度匀速行驶。突然,司机看见车的正前方34m 处有一只狗,如图甲所示,司机立即采取制动措施。司机的反应时间为0.5 s,若从司机看见狗开始计时(t=0),长途客车的v-t 图像如图乙所示。
(1)求长途客车制动时的加速度;
(2)求长途客车从司机发现狗至停止运动的这段时间内前进的距离;
(3)若狗正以v1=4m/s 的速度与长途客车同向奔跑,通过计算分析狗能否摆脱被撞的噩运?
16.如图所示,一平直路面上前、后两车分别以、的匀速行驶,当两车相距时,前车刹车灯亮起,以做匀减速直线运动。
(1)若发现前车刹车灯亮起,后车立即以的加速度制动,后车能否追上前车?(请写出分析过程)
(2)若发现前车刹车灯亮起,后车仍以原速匀速行驶,两车之间的最大距离是多少?
(3)若发现前车刹车灯亮起,后车仍以原速匀速行驶,经过多长时间后车追上前车?
2.5 匀变速直线运动与汽车安全行驶
追及相遇问题 (解析版)
1.(多选)如图所示是做直线运动的甲、乙两物体的位移—时间图像,由图像可知( )
A.甲起动的时间比乙晚t1秒
B.当t=t2时两物体相遇
C.当t=t2时两物体相距最远
D.当t=t3时两物体相距s0米
【答案】BD
【解析】由甲、乙两物体位移—时间图像可知,乙比甲晚运动t1秒,t2时刻位移相等,甲、乙相遇。t3时刻s甲=0,s乙=s0,两物体相距s0,A、C错误,B、D正确。
2.(多选)如图所示,计时开始时A、B两质点在同一位置,由图可知( )
A.A、B两质点运动方向相反
B.2 s末A、B两质点相遇
C.2 s末A、B两质点速度大小相等,方向相同
D.A、B两质点速度相同时,相距6 m
【答案】CD
【解析】A质点做匀减速直线运动,B质点做初速度为零的匀加速直线运动。两质点从同一出发点,同时向同一方向运动。交点表示两质点在2 s这一时刻有相同的速度。这时两质点间有最大距离,因质点的位移对应于图线与坐标及坐标轴所围成的面积,故这最大距离s可由对应于质点A位移的梯形面积与对应于质点B位移的三角形面积之差来求。即
s=s1-s2= m-×2×2 m=6 m
应了解速度图线不同于位移图线,位移图线相交表示在同一位置,而速度图线相交则表示速度相同。
3.(多选)两物体在同一直线上,同时由同一位置向同一方向运动,其速度图像如图所示,下列说法中正确的是( )
A.开始阶段B跑在A的前面,20 s后B落在A后面
B.20 s末B追上A,且A、B速度相等
C.40 s末A追上B
D.在A追B之间的20 s末,两物体相距最远
【答案】CD
【解析】图线所围的面积大小表示物体运动的位移,从图中可知40 s时,两物体相遇,之前B一直在A前面,故选项C正确,当A、B速度相同时相距最远,故选项D正确。
4.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标。在描述两车运动的v-t图中(如图所示),直线a、b分别描述了甲、乙两车在0~20 s的运动情况。关于两车之间的位置关系,下列说法正确的是( )
A.在0~10 s内两车逐渐靠近
B.在10~20 s内两车逐渐远离
C.在5~15 s内两车的位移相等
D.在t=10 s时两车在公路上相遇
【答案】C
【解析】由v-t图像可知,0~10 s内,v乙>v甲,两车逐渐远离,10~20 s内,v乙<v甲,两车逐渐靠近,故选项A、B均错;
v-t图线与时间轴所围的面积的数值表示位移,5~15 s内,两图线与t轴包围的面积相等,故两车的位移相等,选项C对;t=20 s时,两车的位移再次相等,说明两车再次相遇,故D错。
5.甲车静止在一平直公路上,乙车以大小为6m/s的速度做匀速直线运动从甲车旁经过,甲车立即做初速为零的匀加速直线运动,经过4s恰好追上乙车,不考虑车辆尺寸,则( )
A.追上乙车时,甲车的速度大小为6m/s
B.追上乙车时,甲车的速度大小为24m/s
C.甲车匀加速直线运动的加速度大小为1m/s2
D.甲车匀加速直线运动的加速度大小为3m/s2
【答案】D
【解析】CD.甲乙两车位移相等,有
解得甲车匀加速直线运动的加速度大小为
a=3m/s2
选项C错误,D正确;
AB.追上乙车时,由
甲车的速度大小12m/s,选项AB错误。
故选D。
6.甲、乙两辆汽车沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动状况的描述正确的是( )
A.在第末,乙车改变运动方向
B.在第末,甲、乙两车可能相距
C.在第末,甲、乙两车一定相遇
D.两车不可能相遇两次
【答案】B
【解析】A.乙车在10内朝正方向做匀减速直线运动,10s后朝正方向做匀加速直线运动,故在第末,乙车没有改变运动方向,A错误;
BC.题中未指明甲、乙两车出发位置的关系,故在第末,甲、乙两车可能相距,在第末,甲、乙两车可能相遇,也可能不相遇,B正确,C错误;
D.若开始时甲在乙后方,甲先超过乙一次,然后乙速度逐渐增大,再超过甲一次,故两车可能相遇两次,D错误。
故选B。
7.两辆完全相同的汽车,沿平直公路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车。已知前车在刹车过程中前行的距离为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为( )
A.s B.2s
C.3s D.4s
【答案】B
【解析】依题意可画出两车的速度图像如图所示。图线Ⅰ表示前车以恒定加速度刹车时的运动情况,在它刹车时后车以图线Ⅱ继续前进,当前车停止时,后车开始以相同的加速度刹车,如图线Ⅲ(Ⅲ与Ⅰ平行),前车刹车经过的位移为△AOB的“面积”,其大小为s,要保证两车不相撞,两车在匀速行驶时保持的距离s′至少为 ABDC的“面积”,它等于△AOB“面积”的2倍,即s′=2 s。答案选B。
8.甲、乙两名运动员在泳池里训练,时刻从泳池的两端出发,甲、乙的速度-时间图象分别如图1、2所示,若不计转向的时间且持续运动,两运动员均可视为质点。下列说法正确的是( )
A.游泳池长
B.两运动员一定不会在泳池的两端相遇
C.从时刻起经过两运动员共相遇了3次
D.在内,两运动员的平均速度大小之比为
【答案】C
【解析】
A.根据图线与坐标轴围成的图形面积表示位移,可知游泳池长度
或者
故A错误;
B.如图所示
由甲、乙的位移-时间图线的交点表示相遇可知,甲、乙在时在泳池的一端相遇,故B错误;
C.在内甲、乙相遇3次,故C正确;
D.在内,甲的位移大小为
乙的位移大小为
在内两运动员的平均速度大小之比为
故D错误。
故选C。
9.汽车正以10m/s的速度在平直公路上前进,突然发现正前方距离s远处有一辆自行车以4m/s的速度作同方向的匀速直线运动,汽车立即关闭油门作匀减速运动,加速度大小为6m/s2,若汽车恰好不碰上自行车,则s大小为( )
A.3m B.4m C.5m D.6m
【答案】A
【解析】
当两者速度相等时,相距最近,有
v1+at=v2
解得
t=1s
此时汽车前进的距离为
自行车前进的距离为
若汽车恰好不碰上自行车,则s的大小为
故选A。
10.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,时刻同时经过公路旁的同一个路标。在如图描述两车运动的图中,直线a、b分别描述了甲、乙两车在的运动情况。关于两车之间的位置关系,下列说法正确的是( )
A.在内两车逐渐靠近
B.在内两车逐渐远离
C.在时两车在公路上相遇
D.在内两车的位移相等
【答案】D
【解析】
A.在秒内,乙车在甲的前方,而且乙的速度大于甲的速度,则两车逐渐远离,A错误;
B.在秒内,乙车在甲的前方,乙的速度小于甲的速度,则两车逐渐靠近,B错误;
C.根据图象的“面积”等于物体的位移大小,可以看出,在秒时乙车的位移大于甲车的位移,时刻又在同一位置出发,所以在秒时两车没有相遇,C错误;
D.在秒内两车图线的“面积”相等,则通过的位移相等,D正确。
故选D。
11.有甲、乙两车在两条平行车道上沿同一方向直线行驶。时刻,甲车从静止开始以加速度匀加速运动,乙车以的初速度、加速度匀加速运动,时刻两车车头齐平,则下次两车车头齐平的时刻为( )
A. B. C. D.
【答案】A
【解析】
内,甲和乙的位移为
故有
说明时刻甲在乙的前方,设下次车头齐平的时刻为t,
化简得
解得
或
故选A。
12.甲、乙两车在同一水平公路上,一前一后相距x=6m,乙车在前,甲车在后,某时刻两车同时开始运动,两车运动的过程如图所示,则下列说法正确的是( )
A.当t=4s时两车相遇
B.当t=4s时乙车在前,甲车在后
C.两车有两次相遇
D.两车有三次相遇
【答案】D
【解析】
AB.速度图线与时间轴围成的面积表示位移,则知当t=4s时,甲的位移大于乙的位移,0-4s,甲的位移为
x甲=×(16+8)×4m=48m
乙的位移为
x乙=×(12+8)×4m=40m
位移之差
Δx=x甲-x乙=8m
开始时,甲、乙两车在同一水平道路上,一前一后相距x=6m,由此可知,t=4s时,甲车在前,乙车在后,相距2m,故AB错误;
CD.t=4s时,甲车在前,乙车在后,所以两车第一次相遇发生在4s之前;当t=6s时,甲的位移为
x′甲=×(16+4)×6m=60m
乙的位移为
x′乙=×(12+6)×6m=54m
位移之差等于6m,而两车是从开始出发时,甲、乙两车在同一水平道路上,一前一后相距x=6m,所以当t=6s时两车第二次相遇;t=6s后,由于乙的速度大于甲的速度,乙又跑到前面,8s后,由于甲的速度大于乙的速度,两车还会发生第三次相遇,故C错误,D正确。
故选D。
13.甲、乙两车同时从同一地点出发,向同一方向运动,其中,甲以10 m/s的速度匀速行驶,乙以2 m/s2的加速度由静止启动。求:
(1)经过多长时间乙车追上甲车?此时,甲、乙两车速度有何关系?
(2)追上前经多长时间两者相距最远?此时两者的速度有何关系?
【答案】
【解析】
(1)设追上所用时间为t
由s甲=s乙得v甲t=a乙t2
10t=×2×t2
t=10 s
此时v乙=a乙t=2×10 m/s=20 m/s=2v甲
(2)相距最远时满足v乙=v甲=10 m/s
解得时间t′== s=5 s。
答案:(1)10 s v乙=2v甲 (2)5 s v乙=v甲
14.一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车旁边经过。求:
(1)汽车追上自行车前的最远距离;
(2)汽车经多长时间追上自行车?追上自行车时汽车的瞬时速度多大?
【答案】(1)6 m (2)4 s 12 m/s
【解析】本题考查追及问题的求解,关键是找到达到最大距离的临界条件。
法一:物理分析的方法
(1)汽车“追赶”自行车,它们的间距先增后减,当二者速度相同时,间距最大。设二者速度相同,均为6 m/s,所经过的时间为t1,则at1=v自,t1== s=2 s。最大间距Δs=v自t1-at12=(6×2-×3×22) m=6 m。
(2)汽车追上自行车所用时间为t2,则v自t2=at22,即6t2=×3×t22,t2=4 s,此时汽车速度v2=at2=12 m/s。
法二:数学的方法
(1)经过时间t,二者间距为
Δs=v自t-at2=6t-×3×t2=-(t-2)2+6,
当t=2 s时,间距最大,Δsm=6 m。
(2)追上时解法同法一。
法三:图像法
根据题意,从汽车启动瞬间计时,分别作出汽车与自行车的v-t图像,如图所示:
(1)由图像可知,2 s前自行车与汽车间距增大,2 s后汽车“追赶”自行车,它们的间距减小,因此2 s末时刻二者间距最大,最大距离与三角形OAB面积数值相等,即Δsm=6×2× m=6 m。
(2)当所画阴影三角形OAB与三角形CDB面积相等时汽车追上自行车,由两三角形全等可知,在t=4 s时追上自行车,由图像知此时汽车速度为12 m/s。
15.一辆长途客车正在以v0=20m/s 的速度匀速行驶。突然,司机看见车的正前方34m 处有一只狗,如图甲所示,司机立即采取制动措施。司机的反应时间为0.5 s,若从司机看见狗开始计时(t=0),长途客车的v-t 图像如图乙所示。
(1)求长途客车制动时的加速度;
(2)求长途客车从司机发现狗至停止运动的这段时间内前进的距离;
(3)若狗正以v1=4m/s 的速度与长途客车同向奔跑,通过计算分析狗能否摆脱被撞的噩运?
【答案】(1);(2)50m;(3)狗能摆脱被撞的噩运
【解析】
(1)根据图像可得
(2)速度图象与时间轴围成的面积等于物体通过的位移,则有
(3)当客车速度减为与狗的速度相同时,所需时间为
司机从看到狗到速度减为与狗速度相同时,通过位移为
则有
所以狗不会被撞。
16.如图所示,一平直路面上前、后两车分别以、的匀速行驶,当两车相距时,前车刹车灯亮起,以做匀减速直线运动。
(1)若发现前车刹车灯亮起,后车立即以的加速度制动,后车能否追上前车?(请写出分析过程)
(2)若发现前车刹车灯亮起,后车仍以原速匀速行驶,两车之间的最大距离是多少?
(3)若发现前车刹车灯亮起,后车仍以原速匀速行驶,经过多长时间后车追上前车?
【答案】(1)不能;(2);(3)
【解析】
(1)设后车为A,前车为B,A车刹车减速至0时刚好追上B车,则有
代入数据得
因为,故不能追上前车;
(2)当前、后两车速度相等时,相距最远,根据速度关系得
代入数据解得
此时,根据位移公式得
。
代入数据解得
(3)B车从刹车到停止运动所用时间
所发生位移
此时
则
可见此时A车并未追上B车,而是在B车停止后才追上,之后A车运动时间为
故所求时间为
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
