广东省广州市天河区2023-2024学年九年级下学期开学考试数学试题(无答案)
文档属性
| 名称 | 广东省广州市天河区2023-2024学年九年级下学期开学考试数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 567.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 11:29:24 | ||
图片预览


文档简介
2023—2024学年度第二学期
初三级数学科开学练习
本试卷分选择题和非选择题两部分,共4页,满分120分.考试用时120分钟.
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或者签字笔将自己的姓名和学号填写在答题卡相应的位置上,用2B铅笔将字迹的学号填涂在答题卡上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑;如图改动,用橡皮擦干净后,再选涂其它答案:不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔在答卷纸上作答,答案必须写在答卷纸各题目指定区域内的相应位置上,超出指定区域的答案无效:如需改动,先划掉原来的答案,然后再写上新的答案:不准使用铅笔和涂改液,不按以上要求作答的答案无效.
第一部分选择题(共30分)
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列图形中是中心对称图形的是( )
A. B. C. D.
2.二次函数的对称轴为( )
A. B. C. D.
3.如图,点B在反比例函数的图象上,轴于点A,连接OB,则的面积是( )
A. B. C.3 D.6
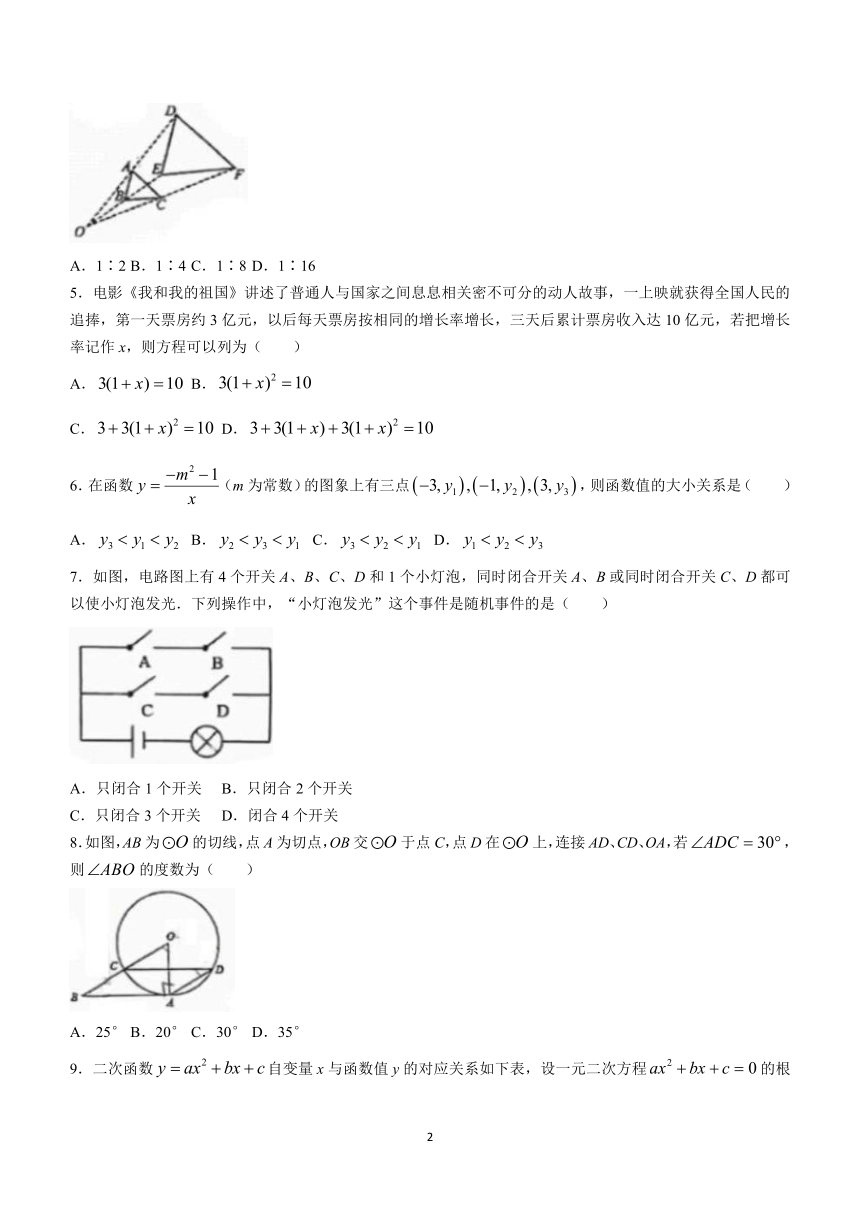
4.如图,与位似,点O为位似中心.已知,则与的面积比为( )
A.1∶2 B.1∶4 C.1∶8 D.1∶16
5.电影《我和我的祖国》讲述了普通人与国家之间息息相关密不可分的动人故事,一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把增长率记作x,则方程可以列为( )
A. B.
C. D.
6.在函数(m为常数)的图象上有三点,则函数值的大小关系是( )
A. B. C. D.
7.如图,电路图上有4个开关A、B、C、D和1个小灯泡,同时闭合开关A、B或同时闭合开关C、D都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
A.只闭合1个开关 B.只闭合2个开关
C.只闭合3个开关 D.闭合4个开关
8.如图,AB为的切线,点A为切点,OB交于点C,点D在上,连接AD、CD、OA,若,则的度数为( )
A.25° B.20° C.30° D.35°
9.二次函数自变量x与函数值y的对应关系如下表,设一元二次方程的根为,且,则下列说法正确的是( )
x 0 0.5 1 1.5 2 2.5
y 0.13 0.38 0.53 0.58 0.53 0.38 0.13
A. B. C. D.
10.如图,在中,.按照如下步骤作图:
①分别以点A,B为圆心,大于的长为半径作弧,两弧相交于点M,N;
②作直线MN,交AC点D;
③以D为圆心,BC长为半径作弧,交AC的延长线于点E;
④连接BD,BE.
下列说法错误的是( )
A. B. C. D.
第二部分 非选择题(共90分)
二、填空题(本大题共6小题,每小题3分,共18分)
11.布袋里有6个大小相同的乒乓球,其中2个为红色,1个为白色,3个为黄色,搅匀后从中随机摸出一个球是红色的概率是______.
12.方程两个根的和为a,两个根的积为b,则______.
13.如图,圆锥的母线长l为10cm,底面圆半径r为4.5cm,则该圆锥的侧面积为______.
14.如图,在中,,将在平面内绕点A旋转到的位置,使则旋转角的度数为______.
15.如图,在平面直角坐标系中,矩形ABCD对角线的交点为坐标原点O,点、D在反比例函数的图象上,点A、C在x轴上,则矩形ABCD的面积为______.
16.如图,抛物线与y轴交于点A,与x轴交于B、C,点A关于抛物线对称轴的对称点为点D,点E在y轴上,点F在以点C为圆心,半径为1.5的圆上,则D的坐标是______,的最小值是______.
三、解答题(本题共9小题,满分72分,解答题需写出必要的文字说明,推理过程和演算步骤)
17.(4分)解方程:
18.(4分)如图,等边的边长为3,P为BC上一点,且,D为AC上一点.若,求CD的长.
19.(6分)如图,已知中.
(1)画出绕着原点O按顺时针方向旋转90°后的图形,记为.
(2)求第(1)问中线段AO旋转时扫过的面积.
20.(6分)如图,一次函数的图像与x轴、y轴分别相交于A、B两点,且与反比例函数的图像在第一象限交于点C,若,B是线段AC的中点.
(1)求一次函数和反比例函数的解析式.
(2)直接写出不等式的解集.
21.(8分)“中国梦”关系每个人的幸福生活,为展现执信人追梦的风采,执信中学举行“中国梦·我的梦”的演讲比赛.赛后整理参赛学生的成绩,将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
(1)参加比赛的学生人数共有______名,在扇形统计图中,表示“D等级”的扇形的圆心角为______度,图中m的值为______;
(2)补全条形统计图。
(3)组委会决定从本次比赛中获得A等级的学生中,选出2名去参加广州市中学生演讲比赛,已知A等级中男生有1名,请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率.
22.(10分)如图,AB为的直径,C、D为圆上两点,.
(1)尺规作图:作于E(保留作图痕迹,不用写作图步骤);
(2)求证:CE是的切线。
(3)若,求CE的长度.
23.(10分)网络销售已经成为一种热门的销售方式,为了减少农产品的库存,某市长亲自在某网络平台上进行直播销售板栗.为提高大家购买的积极性,直播时板栗公司每天拿出2000元现金,作为红包发给购买者,已知该板栗的成本价格为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足关系式:,经销售发现,销售单价不低于成本价格且不高于30元/kg当每日销售量不低于4000kg时,每千克成本将降低1元,设板栗公司销售该板栗的日获利为W(元).
(1)当日销售量不低于4000kg时,x的取值范围是______;
(2)请求出日获利W与销售单价x之间的函数关系式;
(3)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
24.(12分)已知BD是四边形ABCD的对角线,,点E沿A→B→C运动,到达点C时停止运动.点F在线段BD运动,且始终保持,射线AF交线段DE于点P.
图1 图2
(1)如图1,当点E在线段AB上时:
①求证:.
②若,求的度数。
(2)如图2,若点E在线段BC上,G是线段CD中点,在图2中,仅用无刻度度尺在线段DE上作出点P.
(3)请求出点P运动的路径长.
25.(12分)二次函数的顶点M是直线和直线的交点.
(1)若直线过点,求M点坐标及二次函数的解析式;
(2)试证明无论m取任何值,二次函数的图象与直线总有两个不同的交点;
(3)在(1)的条件下,若二次函数的图象与y轴交于点C,与x轴的右交点为A.试在直线上求异于M的点P,使P在的外接圆上.
初三级数学科开学练习
本试卷分选择题和非选择题两部分,共4页,满分120分.考试用时120分钟.
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或者签字笔将自己的姓名和学号填写在答题卡相应的位置上,用2B铅笔将字迹的学号填涂在答题卡上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑;如图改动,用橡皮擦干净后,再选涂其它答案:不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔在答卷纸上作答,答案必须写在答卷纸各题目指定区域内的相应位置上,超出指定区域的答案无效:如需改动,先划掉原来的答案,然后再写上新的答案:不准使用铅笔和涂改液,不按以上要求作答的答案无效.
第一部分选择题(共30分)
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列图形中是中心对称图形的是( )
A. B. C. D.
2.二次函数的对称轴为( )
A. B. C. D.
3.如图,点B在反比例函数的图象上,轴于点A,连接OB,则的面积是( )
A. B. C.3 D.6
4.如图,与位似,点O为位似中心.已知,则与的面积比为( )
A.1∶2 B.1∶4 C.1∶8 D.1∶16
5.电影《我和我的祖国》讲述了普通人与国家之间息息相关密不可分的动人故事,一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把增长率记作x,则方程可以列为( )
A. B.
C. D.
6.在函数(m为常数)的图象上有三点,则函数值的大小关系是( )
A. B. C. D.
7.如图,电路图上有4个开关A、B、C、D和1个小灯泡,同时闭合开关A、B或同时闭合开关C、D都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
A.只闭合1个开关 B.只闭合2个开关
C.只闭合3个开关 D.闭合4个开关
8.如图,AB为的切线,点A为切点,OB交于点C,点D在上,连接AD、CD、OA,若,则的度数为( )
A.25° B.20° C.30° D.35°
9.二次函数自变量x与函数值y的对应关系如下表,设一元二次方程的根为,且,则下列说法正确的是( )
x 0 0.5 1 1.5 2 2.5
y 0.13 0.38 0.53 0.58 0.53 0.38 0.13
A. B. C. D.
10.如图,在中,.按照如下步骤作图:
①分别以点A,B为圆心,大于的长为半径作弧,两弧相交于点M,N;
②作直线MN,交AC点D;
③以D为圆心,BC长为半径作弧,交AC的延长线于点E;
④连接BD,BE.
下列说法错误的是( )
A. B. C. D.
第二部分 非选择题(共90分)
二、填空题(本大题共6小题,每小题3分,共18分)
11.布袋里有6个大小相同的乒乓球,其中2个为红色,1个为白色,3个为黄色,搅匀后从中随机摸出一个球是红色的概率是______.
12.方程两个根的和为a,两个根的积为b,则______.
13.如图,圆锥的母线长l为10cm,底面圆半径r为4.5cm,则该圆锥的侧面积为______.
14.如图,在中,,将在平面内绕点A旋转到的位置,使则旋转角的度数为______.
15.如图,在平面直角坐标系中,矩形ABCD对角线的交点为坐标原点O,点、D在反比例函数的图象上,点A、C在x轴上,则矩形ABCD的面积为______.
16.如图,抛物线与y轴交于点A,与x轴交于B、C,点A关于抛物线对称轴的对称点为点D,点E在y轴上,点F在以点C为圆心,半径为1.5的圆上,则D的坐标是______,的最小值是______.
三、解答题(本题共9小题,满分72分,解答题需写出必要的文字说明,推理过程和演算步骤)
17.(4分)解方程:
18.(4分)如图,等边的边长为3,P为BC上一点,且,D为AC上一点.若,求CD的长.
19.(6分)如图,已知中.
(1)画出绕着原点O按顺时针方向旋转90°后的图形,记为.
(2)求第(1)问中线段AO旋转时扫过的面积.
20.(6分)如图,一次函数的图像与x轴、y轴分别相交于A、B两点,且与反比例函数的图像在第一象限交于点C,若,B是线段AC的中点.
(1)求一次函数和反比例函数的解析式.
(2)直接写出不等式的解集.
21.(8分)“中国梦”关系每个人的幸福生活,为展现执信人追梦的风采,执信中学举行“中国梦·我的梦”的演讲比赛.赛后整理参赛学生的成绩,将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
(1)参加比赛的学生人数共有______名,在扇形统计图中,表示“D等级”的扇形的圆心角为______度,图中m的值为______;
(2)补全条形统计图。
(3)组委会决定从本次比赛中获得A等级的学生中,选出2名去参加广州市中学生演讲比赛,已知A等级中男生有1名,请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率.
22.(10分)如图,AB为的直径,C、D为圆上两点,.
(1)尺规作图:作于E(保留作图痕迹,不用写作图步骤);
(2)求证:CE是的切线。
(3)若,求CE的长度.
23.(10分)网络销售已经成为一种热门的销售方式,为了减少农产品的库存,某市长亲自在某网络平台上进行直播销售板栗.为提高大家购买的积极性,直播时板栗公司每天拿出2000元现金,作为红包发给购买者,已知该板栗的成本价格为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足关系式:,经销售发现,销售单价不低于成本价格且不高于30元/kg当每日销售量不低于4000kg时,每千克成本将降低1元,设板栗公司销售该板栗的日获利为W(元).
(1)当日销售量不低于4000kg时,x的取值范围是______;
(2)请求出日获利W与销售单价x之间的函数关系式;
(3)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
24.(12分)已知BD是四边形ABCD的对角线,,点E沿A→B→C运动,到达点C时停止运动.点F在线段BD运动,且始终保持,射线AF交线段DE于点P.
图1 图2
(1)如图1,当点E在线段AB上时:
①求证:.
②若,求的度数。
(2)如图2,若点E在线段BC上,G是线段CD中点,在图2中,仅用无刻度度尺在线段DE上作出点P.
(3)请求出点P运动的路径长.
25.(12分)二次函数的顶点M是直线和直线的交点.
(1)若直线过点,求M点坐标及二次函数的解析式;
(2)试证明无论m取任何值,二次函数的图象与直线总有两个不同的交点;
(3)在(1)的条件下,若二次函数的图象与y轴交于点C,与x轴的右交点为A.试在直线上求异于M的点P,使P在的外接圆上.
同课章节目录
