第十一章《简单机械和功》 11.1 杠杆 课件(共74张ppt) 苏科版九年级上册物理
文档属性
| 名称 | 第十一章《简单机械和功》 11.1 杠杆 课件(共74张ppt) 苏科版九年级上册物理 |

|
|
| 格式 | pptx | ||
| 文件大小 | 50.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-07 17:33:29 | ||
图片预览






文档简介
第十一章
江苏科学技术出版社
简单机械和功
九年级物理上册?苏科版
延伸人体的“神臂”
从我们吃饭用的筷子,
到航天器使用的机械臂。
机械已深入到人类生活的方方面面,
无论多么复杂的机械都是由简单机械组成的。
我们在叹服于机械的神奇和人类伟大智慧的同时,
不禁产生许多遐想………
这些机械是依据什么原理工作的呢?
第十一章
江苏科学技术出版社
简单机械和功
九年级物理上册?苏科版
延伸人体的“神臂”
从我们吃饭用的筷子,
到航天器使用的机械臂。
机械已深入到人类生活的方方面面,
无论多么复杂的机械都是由简单机械组成的。
我们在叹服于机械的神奇和人类伟大智慧的同时,
不禁产生许多遐想………
这些机械是依据什么原理工作的呢?
杠杆的平衡条件
什么是杠杆
生活中的杠杆
一、杠杆
1
导入新课
人类很早以前就学会使用杠杆了。壮丽辉煌的咸阳宫曾蔚然矗立于八百里秦川。司马迁在《史记》中有关于这座宫殿的描述。下图就是我们的祖先在建造宫殿时的情景。你能讲出其中的道理吗?
阿基米德的豪言壮语对吗?包含着怎样的知识?
若给我一个立足点和一根足够长的棒,我可以搬动地球。
学习了“杠杆” 你就明白了,今天我们一起学习。
两千多年前古希腊哲学家、数学家、物理学家——阿基米德曾说过这样的豪言壮语:
第1节 杠杆
2
学习新课
11.1 拔图钉
活 动
做一做
木板上钉了一枚图钉,你能直接用手把它拔出来吗?
议一议
你是怎样拔出这枚图钉的?有哪些不同的方法?哪一种方法更方便、省力?
请从图中选择合适的工具把图钉拔出来。
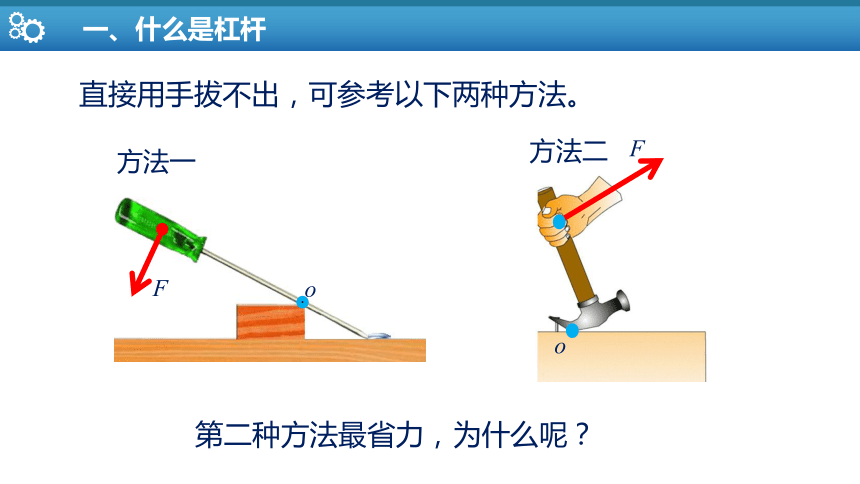
方法一
方法二
F
o
直接用手拔不出,可参考以下两种方法。
F
o
第二种方法最省力,为什么呢?
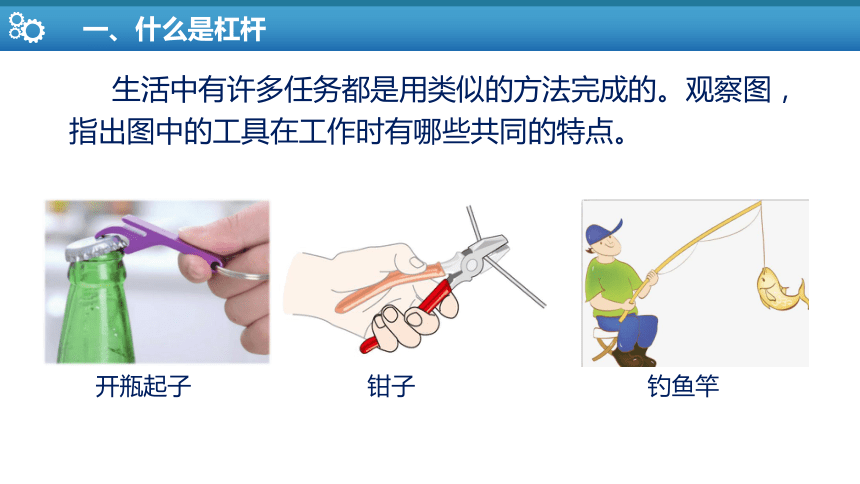
生活中有许多任务都是用类似的方法完成的。观察图,指出图中的工具在工作时有哪些共同的特点。
开瓶起子 钳子 钓鱼竿
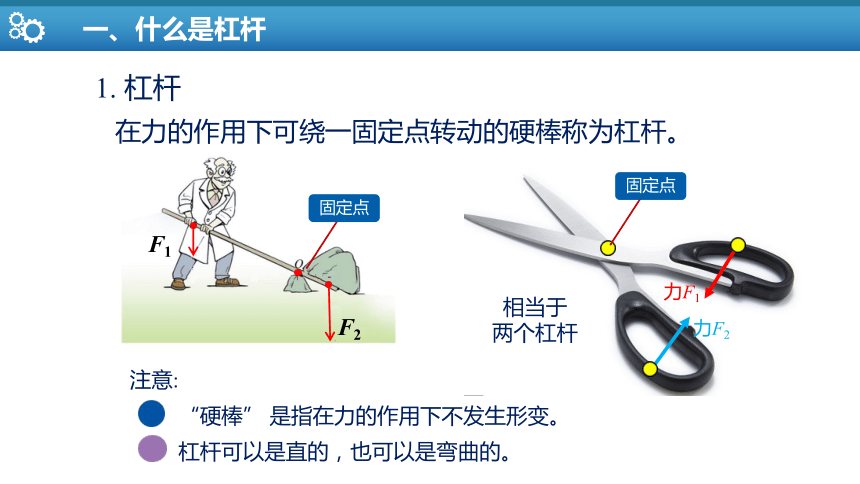
F1
F2
力F1
力F2
相当于
两个杠杆
注意:
“硬棒” 是指在力的作用下不发生形变。
杠杆可以是直的,也可以是弯曲的。
固定点
固定点
1. 杠杆
在力的作用下可绕一固定点转动的硬棒称为杠杆。
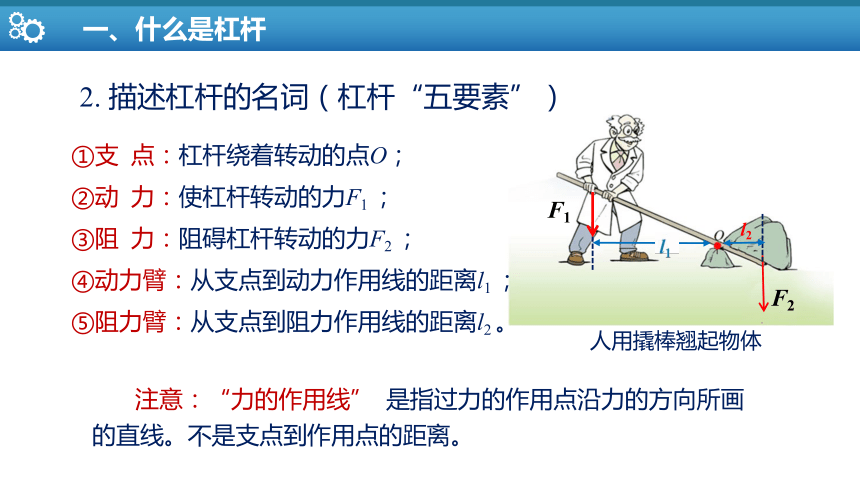
2. 描述杠杆的名词(杠杆“五要素”)
①支 点:杠杆绕着转动的点O;
②动 力:使杠杆转动的力F1 ;
③阻 力:阻碍杠杆转动的力F2 ;
④动力臂:从支点到动力作用线的距离l1 ;
⑤阻力臂:从支点到阻力作用线的距离l2 。
注意:“力的作用线” 是指过力的作用点沿力的方向所画的直线。不是支点到作用点的距离。
F2
F1
l2
人用撬棒翘起物体
3. 进一步理解杠杆的“五要素”
力臂不一定在杠杆上,当力的作用线与杠杆不垂直时,力臂与杠杆不重合。力臂包含了力的作用点和力的方向两个要素。
杠杆可以是直的,也可以是弯的。即杠杆可以是各种各样的形状。
支点一定在杠杆上。动力和阻力可以在支点两侧,也可在支点同侧。作用在杠杆上的动力和阻力使杠杆转动的方向一定是相反的,但动力和阻力的方向不一定相反。
F1的力臂l1
不在杠杆上。
4. 画力臂的要求
从支点O向力的作用线引垂线,画出垂足,则从支点到垂线的距离就是力臂。
过力的作用点沿力的方向画出力的作用线。
注意: 必要时要用虚线将力的作用线延长。
先确定杠杆的支点O和动力、阻力的方向。
最后用大括号或箭头勾出力臂,并在旁边写上字母l1或l2。
动力臂l1
5. 力臂的画法
阻力F2
动力F1
阻力臂l2
以人用撬棒翘起物体为例——画出动力F1与阻力F2的力臂
支点O
力的
作用线
F1
F2
视频欣赏——《杠杆与杠杆的五要素》
【例题1】关于杠杆,下列说法中正确的是( )
A. 杠杆一定是一根直的硬棒
B. 杠杆的支点一定在杠杆上,且在杠杆的中间位置
C. 力臂可能在杠杆上,也可能不在杠杆上
D. 从支点到动力作用点的距离叫动力臂
杠杆是一根硬棒,但不一定是直的,杠杆的支点一定在杠杆上,不一定在杠杆的中间位置,所以A、B选项是错误的。
力臂可能在杠杆上,也可能不在杠杆上,选项C正确;
D选项中,从支点到动力作用线的距离叫动力臂,所以 D选项错误。
???C
故选C。
画力F1的力臂时,只需过支点O做F1的垂线即可;
因为L2是F2的力臂,所以画出与L2垂直的线段,就是力的作用线,
再根据动力与阻力对杠杆的作用效果相反,即可确定阻力F2的方向。
【例题2】如图所示杠杆在力F1、F2的作用下处于静止状态,L2是F2的力臂。请在图中画出力F1的力臂L1以及阻力F2.
F2
l1
∟
【例题3】如图开瓶器开启瓶盖时可抽象为一杠杆,不计自重。选项图能正确表示它工作示意图的是( )
由题图知,向上用力时,起子围绕左端O转动,因此O为支点。又因为动力F1的方向向上,使杠杆沿逆时针转动,所以阻力F2的方向向下,使杠杆沿顺时针转动。故选B。
???B
①为什么体重不同的两人
能让跷跷板水平静止?
在杠杆的使用中,杠杠的平衡状态是一种非常重要的状态。
杠杆满足什么条件时才会平衡呢?下面我们一起探究。
②为什么重力相同的两人
不能让跷跷板水平静止?
1. 杠杆的平衡:
杠杆静止或匀速转动,就说杠杆处于平衡状态。
提出问题
猜想与假设
杠杆平衡时,动力、动力臂、阻力、阻力臂之间存在着怎样的关系?
动力+动力臂=阻力+阻力臂
动力-动力臂=阻力-阻力臂
动力×动力臂=阻力×阻力臂
动力:动力臂=阻力:阻力臂
…………
探究杠杆的平衡条件
学生实验
①实验器材:杠杆、钩码、铁架台、弹簧测力计。
②测量的物理量:力、力臂。
③当杠杆平衡时,分别测出动力F1、阻力F2,动力臂L1、阻力臂L2。并多次改变力和力臂的大小,获取多组数据。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}实验
次数
动力F1/N
动力臂l1/cm
阻力
F2/N
阻力臂l2/cm
1
2
3
设计实验
实验表格
①把杠杆安装在支架上,调节杠杆两端的平衡螺母, 使杠杆在水平位置平衡。
平衡螺母
使杠杆在水平位置平衡时,两个力臂可以直接从杠杆上直接读出,就不用测量了,非常方便。
另外,可以消除杠杆自身的重力对实验结果的影响。
杠杆哪端高,就把平衡螺母向哪端调节;或者杠杆向哪边偏,就把平衡螺母向反方向调节
平衡螺母
实验步骤
②在杠杆两边挂不同数量的钩码,把支点右边的钩码对杠杆的作用力当作动力F1,支点左边的钩码对杠杆的作用力当作阻力F2。
调节钩码的位置,使杠杆在水平位置重新平衡,将动力F1、阻力F2、动力臂L1、阻力臂L2的实验数据填入表中。
实验中所用每个钩码的重力都相等。
③改变阻力和阻力臂的大小,相应调节动力和动力臂的大小,使杠杆在水平位置重新平衡,再做几次实验。
④在杠杆的一侧挂上钩码作为阻力,通过在其他位置上用弹簧测力计拉住杠杆的办法使杠杆平衡。
将动力F1、阻力F2、动力臂l1、阻力臂l2记录在表格中。
注意:
弹簧测力计只有沿竖直方向施加力,才可以直接读出力臂。
F1
o
l1
实验数据记录
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}实验次数
动力F1/N
动力臂l1/cm
阻力F2/N
阻力臂l2/cm
1
2
10
1
20
2
3
10
2
15
3
4
5
1
20
交流与小结
动力×动力臂=阻力×阻力臂,
杠杆平衡时
分析表中的数据,找出它们之间的关系,你从中有什么发现?
杠杆平衡时:动力×动力臂=阻力×阻力臂
计算公式:
F1 L1=F2 L2
注意:
①应用公式计算时,单位要统一,即动力和阻力的单位要用牛(N),动力臂和阻力臂的单位要相同。
②杠杆是否平衡,取决于力和力臂的乘积;乘积相等就平衡;否则沿着乘积大的那端转动。
或变形式:
作用在杠杆上两个力的大小
与他们的力臂成反比。
这就是阿基米德
发现的杠杆原理。
????1????2=????1????2
?
2. 杠杆的平衡条件
①让杠杆在水平位置静止的目的是:
一是使杠杆的重心在支点,以消除杠杆自身重力对实验的影响。二是便于直接读出力臂。
②多次测量获得多组实验数据的目的是:
避免偶然性,获得普遍性的结论。
【评估与交流】
③在实验前要调节杠杆两端的平衡螺母,使杠杆水平平衡。挂钩码后,不能再调节平衡螺母。
④读数时,杠杆仍要保持处于水平平衡状态,以便直接读出力臂的长度。
调节
平衡螺母
不能调节
平衡螺母
(b)
(a)
l2
∟
⑤弹簧测力计一定沿竖直方向施加力。
如图(a)所示,弹簧测力计沿竖直方向施加力时,力臂l1是10cm。如果弹簧测力计不沿竖直方向施加力, 如图(b)所示,则力臂为l2,
l2 < l1,将小于10cm,变小。
l1
视频演示《实验—探究杠杆的平衡条件》
【例题4】如图所示,小明利用铁架台、带有刻度的杠杆、细线、弹簧测力计、若干钩码(每个钩码重均为0.5N)等实验器材,探究杠杆的平衡条件。
①实验前,杠杆静止在甲所示的位置,则此时杠杆处于 ??(选填“平衡”或“不平衡”)状态;要使杠杆在水平位置平衡,应将平衡螺母向 调节,这样做的目的是消除杠杆自重对实验的影响。
②将杠杆调整好后,如图乙所示,在A点挂3个钩码,则应在B点挂 个钩码,才能使杠杆在水平位置平衡。
③如图丙所示,小明用弹簧测力计替代钩码,先在B点竖直向下拉使杠杆平衡,然后将弹簧测力计逐渐向右倾斜,要使杠杆仍然在水平位置平衡,则弹簧测力计的示数将逐渐_______(选填“变大”或“变小”),原因是__________。
④在实验中,改变力和力臂的大小得到多组数据的目的是:
_____(填序号)。
A. 使测量数据更准确
B. 多次测量取平均值减小误差
C. 避免偶然性,使实验结论具有普遍性
解析见下页
①实验前,杠杆静止在图甲所示的位置,则此时杠杆处于 ?(选填“平衡”或“不平衡”)状态;要使杠杆在水平位置平衡,应将平衡螺母向 调节,这样做的目的是消除杠杆自重对实验的影响。
②将杠杆调整好后,如图乙所示,在A点挂3个钩码,则应在B点挂 个钩码,才能使杠杆在水平位置平衡。
①杠杆静止在图甲位置,此时处于平衡状态;调节杠杆在水平位置平衡,杠杆的左端上翘,平衡螺母向上翘的左端移动。
②由杠杆平衡条件F1l1=F2l2得3G1×2l=nG1×3l,n=2,故在B点挂2个钩码。
平衡
左
2
③如图丙所示,小明用弹簧测力计替代钩码,先在B点竖直向下拉使杠杆平衡,然后将弹簧测力计逐渐向右倾斜,要使杠杆仍然在水平位置平衡,则弹簧测力计的示数将逐渐_______(选填“变大”或“变小”),原因是_________________。
④在实验中,改变力和力臂的大小得到多组数据
的目的是:_____(填序号)。
A.使测量数据更准确
B.多次测量取平均值减小误差
C.避免偶然性,使实验结论具有普遍性
③当拉力F向右倾斜时,力臂变小,要保持杠杆仍在水平位置平衡,根据杠杆的平衡条件,因阻力和阻力臂不变,则拉力F将变大。
④实验测多组数据的目的是使得出的结论更具有普遍性,故选C。
变大
拉力力臂变小
C
①如图所示,是利用撬棒撬石头时的情景,请仔细观察,它的动力臂和阻力臂,哪个更长呢?
我们在使用时,是省力?还是费力呢?
②如图所示,是利用食品夹时的情景,请仔细观察,它的动力臂和阻力臂,哪个更长呢?
根据杠杆的平衡条件对杠杆进行分析:
>
省力杠杆
等臂杠杆
费力杠杆
=
<
提示:判断杠杆的类型,实际就是比较动力臂和阻力臂的大小。
如图所示,人的动力为F1 ,动力臂为l1 ;阻力为F2,阻力臂为l2。
若l1<l2,则F1 F2
若l1= l2,则F1 F2
若l1>l2,则F1 F2
根据杠杆的平衡条件:F1 L1=F2 L2
①特点:动力臂大于阻力臂,省力费距离。
o
F1
F2
使用省力杠杆时,动力移动的距离A0A大于阻力移动的距离BB0,即费距离。
因为l1>l2,所以F1 <F2,即省力。
根据杠杆的平衡条件:F1 L1=F2 L2
1. 省力杠杆
②省力杠杆的实例分析
F1
F2
o
o
F2
F1
剪刀相当于两个杠杆组合在一起
l2
l1
因为l1>l2,所以F1<F2,即省力。
③生活中的一些省力杠杆:
o
F1
F2
使用费力杠杆时,动力移动的距离h1小于阻力移动的距离h2,即省距离。
F1
F2
h2
h1
因为l1<l2,所以F1 >F2,即费力。
根据杠杆的平衡条件:F1 L1=F2 L2
①特点:动力臂小于阻力臂,费力省距离。
o
2. 费力杠杆
②费力杠杆的实例分析
o
F1
F2
F2
l1
l2
l2
l1
筷子相当于两个杠杆组合在一起。
人的右手与钓鱼竿接触处O为支点。
o
F1
因为l1<l2,所以F1 >F2,即费力。
③生活中的一些费力杠杆
扫把
镊子
船桨
①特点:动力臂等于阻力臂,动力等于阻力,不费距离不省距离。
o
F1
F2
使用等臂杠杆时,动力移动的距离等于阻力移动的距离,即不省距离也不费距离。
因为l1=l2,所以F1=F2 ,即动力等于阻力。
根据杠杆的平衡条件:F1 L1=F2 L2
3. 等臂杠杆
②生活中的等臂杠杆
定滑轮
托盘天平
跷跷板
杠杆分类
力臂关系
省费力、距离情况
应用举例
省力杠杆
费力杠杆
等臂杠杆
省力费距离
省距离费力
不省力也不省距离
撬棍、扳手、钢丝钳
天平、跷跷板
镊子、鱼竿、筷子
l动>l阻
l动<l阻
l动=l阻
4. 总结:杠杠的分类
【例题6】在如图所示的工具中,使用时属于费力杠杆的是( )
B
A.支点在起子与瓶盖中间接触处,动力臂大于阻力臂,是省力杠杆;
B.支点在夹子两壁连接处,动力臂小于阻力臂,是费力杠杆;
C.支点是锤子与地面的接触点,动力臂大于阻力臂,是省力杠杆;
D.支点在夹子两壁连接处,动力臂大于阻力臂,是省力杠杆。
B是费力杠杆,所以选B。
A.瓶盖起子 B.食品夹 C.起钉锤 D.核桃夹
生活?物理?社会
生活中的剪刀
剪刀是生活中常见的工具,它也是一种杠杆。你是否注意到,从事不同行业的人所用的剪刀各有特点?
栽衣剪刀 理发剪刀 剪铁皮剪刀 修枝剪刀
根据杠杆的平衡条件:
F1 L1=F2 L2
人所用的力:F1 = ????2????1 F2
?
结论:当阻力不变时,被剪物体离支点越近,阻力臂L2越小,动力F1越小(越省力)。
生活?物理?社会
生活中的剪刀
栽缝用的剪刀刀刃比平常家用剪刀的刀刃长得多,完成一次剪裁动作可以裁剪较长的布料。
理发师用的剪刀手柄比较短,他们剪发时手的动作幅度较小,可提高剪发的频率。
剪铁皮的剪刀,其动力臂比阻力臂长,是省力杠杆,只要用较小的力,就能把坚硬的金属片剪开。
生活?物理?社会
生活中的剪刀
园艺师使用的剪刀有很多种,如修整冬青树的势刀、剪花枝的剪刀等,它们各有特点。请你调查一下,园艺师使用了哪些剪刀?它们各有什么特点?为什么这样设计?
粗枝剪
能剪切0-4cm的粗枝,类似老虎钳子。实际上是个省力杠杆。
园艺大剪刀
刀刃比平常剪刀的刀刃长得多,完成一次剪裁动作可以裁剪较多的枝叶。
【例题5】在苏州动物园内,一位物理老师利用杠杆原理,仅用小小的弹簧测力计就测出了一头大象的质量(如图甲)。测量时用了一根长度为12m的槽钢作为杠杆(如下图乙所示),吊钩固定于槽钢的中点O。当槽钢水平静止时,弹簧测力计的示数F1=200N,测得l1为6m,l2为4cm。不计铁笼的质量,请估算大象的质量。 g取10 N/kg 。
甲
乙
L2=4cm=0.04m
由F1l1=F2l2 得:
F2=????1????1????2=200N×6m0.04m=3×104N
即大象的重力G为3×104N
则大象的质量m为
m=????????=3×104N10N/kg
= 3×103kg
?
生活?物理?社会
人体中的杠杆
骨骼、肌肉和关节构成了人体的运动系统,尽管人体的各种运动相当复杂,但最基本的运动都是由骨骼绕关节转动产生的,其模型就是杠杆。例如,当手握哑铃向上运动时,上臂中的肱三头肌伸展、肱二头肌收缩产生的力使前臂骨骼绕肘关节转动。在这里,前臂骨骼可以看成杠杆,肘关节是支点,哑铃对手的压力是阻力,上臂中的肌肉对前臂骨骼施加的力则是动力。
生活?物理?社会
人体中的杠杆
动力臂l1
阻力F2
阻力臂l2
支点O
动力F1
前臂骨骼实质是一个费力杠杆。
因为 l1<l2,
所以 F1> F2
根据杠杆的平衡条件:
F1 L1=F2 L2
生活?物理?社会
人体中的杠杆
如图所示,当手托住铁球并绕腕关节向上转动时,手就是一个杠杆,铁球压在掌心上的力是阻力,腕关节是支点,前臂中的伸肌伸展和屈肌收缩产生动力,使托住铁球的手向上转动.
人体有600多块肌肉,它们在神经系统的控制下,分别负责各部位的运动。当你做抬腿、伸臂、点头、叩齿等动作时,你就用到了身上各种各样的杠杆。
人体中的杠杆为科技工作者的创造和发明提供了很多启示,机器人和国际空间站上的机械臂(p.29)的发明就是其生动的体现。
生活?物理?社会
人体中的杠杆
如图所示,当手托住铁球并绕腕关节向上转动时,手就是一个杠杆,铁球压在掌心上的力是阻力,腕关节是支点,前臂中的伸肌伸展和屈肌收缩产生动力,使托住铁球的手向上转动.
阻力F2
支点O
动力F1
阻力臂l2
前臂骨骼实质是一个费力杠杆。
因为 l1<l2,
所以 F1> F2
根据杠杆的平衡条件:
F1 L1=F2 L2
动力臂l1
3
课堂总结
三类杠杆
力臂关系
省费力、距离情况
应用举例
省力杠杆
l动 l阻
费力杠杆
l动 l阻
等臂杠杆
l动 l阻
②杠杆的五要素:支点、动力、动力臂、阻力、阻力臂。
①杠杆的定义:在力的作用下可绕一固定点转动的硬棒称为杠杆。
③杠杆的平衡条件:动力?动力臂=阻力?阻力臂
F1l1=F2l2
④杠杆分类
杠杆
>
<
=
省力费距离
省距离费力
不省力也不省距离
撬棍、扳手、钢丝钳
天平、跷跷板
镊子、鱼竿、筷子
4
WHAT?WHY?WOW
1. 指出图中各种杠杆工作时的支点、动力、动力臂、阻力和阻力臂,并说明这些杠杆中哪些是省力的,哪些是费力的。
F1
F2
o
l2
F2
o
l2
F1
l1
F2
o
l2
F1
省力杠杆
费力杠杆
省力杠杆
2. 在“探究杠杆的平衡条件“实验中,我们也可用在杠杆支点的两边分别挂钩码的方法,来探究杠杆的平衡条件。如图所示,在杠杆的左边距支点20cm处挂了四个钩码,要使杠杆在水平位置平衡,如何在杠杆的右边挂钩码?(钩码的质量相等)
根据杠杆的平衡条件:
F1 L1=F2 L2
m1 gL1= m2 gL2
m1 L1= m2 L2
若 L2= L1 则 m2 = m1
若 L2=0.5 L1 则m2 =2 m1
所以可在右边20cm处挂4个钩码,或在10cm处挂8个钩码。
3. 小制作:蜡烛跷跷板。
将一支蜡烛的两端削尖,在中间垂直插入一枚大号缝衣针,把缝衣针的两端分别放在两个玻璃杯上,就做成了一个蜡烛跷跷板。用小刀对蜡烛的两端进行加工,使跷跷板能在水平位置平衡。点燃蜡烛的两端,蜡烛跷跷板会怎样运动?你能说明其中的道理吗?
因为缝衣针不可能正好插在蜡烛的重心位置,质量略大的一端向下倾斜,火苗向上烧,使蜡烛的这一端熔化较快,质量很快小于另一端,从而向上翘起(另一端就会下倾);同理,当另一端质量变小后又向上翘起……蜡烛跷跷板就这样不停地往复摆动。
5
课堂练习
1. 如图所示,请画出作用在杠杆B端上最小的动力F1和阻力F2的力臂l2.
F1
∟
l2
∟
作图步骤:
①确定最大力臂:作用在B端上动力F1最小时,则动力臂最大,应该为OB。
②画力的作用线:过B点做与OB垂直的线段(即动力的作用线)。
③确定动力的方向:与阻力F2的作用效果相反,应该向上。
人的右手与鱼竿接触点为支点,左手的力为动力F1,鱼对鱼竿末端的拉力F2为阻力。如图所示。
2. 如图是使用钓鱼竿的示意图,O为支点,F1是手对竿的作用力,F2是鱼线对竿的作用力,请在图中画出F1、F2的力臂。
3.图中杠杆质地均匀,每个钩码重0.5 N,下列操作中可以使杠杆在水平位置平衡的是(杠杆上有等间隔的刻度)( )
D
使杠杆在水平位置平衡,需满足两个力使杠杆转动的方向相反,所以A与C都不能使杠杆水平平衡。
由杠杆的平衡条件:F1l1=F2l2 计算出D图中2N×3=1N×6,所以可以使杠杆平衡。
4. 如图为工地搬运砖头的独轮车,人抬起车把时,车体可以看成个杠杆,关于这个杠杆下列说法正确的是( )
A.手握的位置靠近把手末端时更费力
B.砖头的位置远离车轮时抬起更省力
C.轮子的中心是杠杆的支点
D.图中拉力F大于重力G
A.手握的位置靠近把手末端时,动力臂更长,则更省力,故A错误;
B.砖头的位置远离车轮时,重力的阻力臂变大,故抬起更费力,故B错误;
C.工地搬运砖头的独轮车工作时,车轮中心是支点,故C正确;
D.根据杠杆平衡条件,拉力力臂大于阻力力臂时省力,图中拉力F小于重力G,故D错误。所以选C。
C
5. 如图3所示,O为轻质杠杆AB的支点,B点挂一重物G,若在B点施加F1、或在A点分别施加F2、F3、F4四个力后,杠杆均保持水平位置平衡,则这四个力中最小的力是( )
由图可知,O为支点,力F1与杠杆垂直,则力F1对应的动力臂为OB;力F3与杠杆垂直,则力F3对应的动力臂为OA;
由图可知,F2、F4对应的力臂都小于OA,而OB>OA,所以OB是最大的力臂;
由杠杆平衡条件F1l1=F2l2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小;因为F1对应的动力臂最长,所以F1最小。
故A符合题意,选项B、C、D不符合题意。
A
6. 撬棒是人们在劳动中应用杠杆原理的工具。如图所示是工人利用撬棒撬动大石头的情景,撬棒上O点为杠杆的支点。下列分析正确的是( )
B
A.此时撬棒为等臂杠杆
B.应用此撬棒的主要目的是省力
C.力F的作用点靠近O点会更省力
D.应用此撬棒的主要目的是省距离
ABD选项:由图知,在使用撬棒时,动力臂大于阻力臂,为省力杠杆,使用该杠杆省力但费距离,故B正确、AD错误;
C选项:力F的作用点靠近O点时,动力臂减小,而阻力、阻力臂不变,由杠杆平衡条件可知动力会变大,会更费力,故C错误。
7. 如图4所示为等刻度的轻质杠杆,在A处挂一个重为2牛的物体,若要使杠杆在水平位置平衡,则在B处施加的力( )
解析 子弹在枪膛中受火药爆炸后产生气体的作用力而运动的距离为
枪膛长度,即s=50 cm=0.5 m,子弹离开枪膛后就不再受火药爆炸产生的
气体推力,气体推力不再做功;所以,气体对子弹做功:W=Fs=700 N×0.5 m
=350 J。
设杠杆每一格长度是a,当B处的作用力与杠杆垂直向下时,
力臂最大,此时作用力最小,由杠杆平衡条件可得
FAlA=FB最小lB 即 2N×2L=FB最小×4a 解得 FB最小=1N
当作用在B处的力与杠杆不垂直时,力臂小于4a,作用力大于1N,因此要使杠杆平衡,作用在B处的力F ≥1N,故A符合题意. 选A。
A. 可能是2牛 B. 可能是0.5牛 C. 一定是1牛 D. 一定是4牛
A
8. 如图所示,采石场的工人想用撬棒撬起一块大石头,甲工人说按住撬棒向下施力最省力;乙工人说抬着撬棒向上施力最省力。请你分别作出这两种不同施力方向的最小作用力的示意图,并说明哪种施力方向最省力。(已知C到O1的距离与C到O2的距离相等)
8. 请你分别作出这两种不同施力方向的最小作用力的示意图,并说明哪种施力方向最省力。(已知C到O1的距离与C到O2的距离相等)
两种方法中,最小作用力的示意图如图甲、乙所示;图甲中,O1是支点,动力F甲的力臂为AO1的长;图乙中, O2是支点,动力F乙的力臂为AO2的长。
设石头对杠杆的压力为F压,由杠杆平衡条件知: F甲×AO1=F压×CO1,
F乙×AO2=F压×CO2, ∵ CO1=CO2,AO1F乙,即乙的方法更省力。
乙
甲
杠杆的B点挂重物,在A端通过细绳施加竖直向上、大小为 10牛的拉力F使杠杆水平平衡时,由杠杆平衡条件F1L1 = F2L2可知,
10牛×OA = G×OB 0A :OB= G:10N ………①
如果把重物悬挂点和拉力作用点互换,此时杠杆平衡时,
F1'OB = G×OA 22.5N×0B = G×OA ………②
由①与②得 G?=225 G=15N 所以选B。
9. 如图所示,轻质杠杆OA可绕O点转动。在杠杆的B点挂上重物,在A端通过细绳施加竖直向上10牛的拉力F使杠杆水平平衡。如果把重物悬挂点和拉力作用点互换,当杠杆水平平衡时,竖直向上的拉力大小变为22. 5牛。则该物体的重为( )
A. 12牛 B. 15牛 C. 18牛 D. 21牛
B
10. 如图,轻质均匀杠杆OB长1m,能绕支点O转动,B端用细绳BC竖直悬于C点,有一重力为200N的物块挂在A点,OA长0.3m,求:
①此时绳BC对杠杆的拉力F的大小。
②若绳BC能承受的最大拉力为150N,移动重物到某一位置,绳BC恰好断裂,求重物悬挂点到支点O的距离。
①根据杠杆的平衡条件得 F1l1=F2l2 得:F×OB=G×OA,即
F×1 m=200 N×0.3 m,则 F=60 N
②设重物悬挂点到支点O的距离为L,绳BC恰好断裂,此时最大拉力F′=150 N,根据杠杆的平衡条件得F′×BO=G×L,即150N×1m=200N×L,
则L=0.75 m。即重物悬挂点到支点O的距离为0.75m时,绳BC恰好断裂。
江苏科学技术出版社
简单机械和功
九年级物理上册?苏科版
延伸人体的“神臂”
从我们吃饭用的筷子,
到航天器使用的机械臂。
机械已深入到人类生活的方方面面,
无论多么复杂的机械都是由简单机械组成的。
我们在叹服于机械的神奇和人类伟大智慧的同时,
不禁产生许多遐想………
这些机械是依据什么原理工作的呢?
第十一章
江苏科学技术出版社
简单机械和功
九年级物理上册?苏科版
延伸人体的“神臂”
从我们吃饭用的筷子,
到航天器使用的机械臂。
机械已深入到人类生活的方方面面,
无论多么复杂的机械都是由简单机械组成的。
我们在叹服于机械的神奇和人类伟大智慧的同时,
不禁产生许多遐想………
这些机械是依据什么原理工作的呢?
杠杆的平衡条件
什么是杠杆
生活中的杠杆
一、杠杆
1
导入新课
人类很早以前就学会使用杠杆了。壮丽辉煌的咸阳宫曾蔚然矗立于八百里秦川。司马迁在《史记》中有关于这座宫殿的描述。下图就是我们的祖先在建造宫殿时的情景。你能讲出其中的道理吗?
阿基米德的豪言壮语对吗?包含着怎样的知识?
若给我一个立足点和一根足够长的棒,我可以搬动地球。
学习了“杠杆” 你就明白了,今天我们一起学习。
两千多年前古希腊哲学家、数学家、物理学家——阿基米德曾说过这样的豪言壮语:
第1节 杠杆
2
学习新课
11.1 拔图钉
活 动
做一做
木板上钉了一枚图钉,你能直接用手把它拔出来吗?
议一议
你是怎样拔出这枚图钉的?有哪些不同的方法?哪一种方法更方便、省力?
请从图中选择合适的工具把图钉拔出来。
方法一
方法二
F
o
直接用手拔不出,可参考以下两种方法。
F
o
第二种方法最省力,为什么呢?
生活中有许多任务都是用类似的方法完成的。观察图,指出图中的工具在工作时有哪些共同的特点。
开瓶起子 钳子 钓鱼竿
F1
F2
力F1
力F2
相当于
两个杠杆
注意:
“硬棒” 是指在力的作用下不发生形变。
杠杆可以是直的,也可以是弯曲的。
固定点
固定点
1. 杠杆
在力的作用下可绕一固定点转动的硬棒称为杠杆。
2. 描述杠杆的名词(杠杆“五要素”)
①支 点:杠杆绕着转动的点O;
②动 力:使杠杆转动的力F1 ;
③阻 力:阻碍杠杆转动的力F2 ;
④动力臂:从支点到动力作用线的距离l1 ;
⑤阻力臂:从支点到阻力作用线的距离l2 。
注意:“力的作用线” 是指过力的作用点沿力的方向所画的直线。不是支点到作用点的距离。
F2
F1
l2
人用撬棒翘起物体
3. 进一步理解杠杆的“五要素”
力臂不一定在杠杆上,当力的作用线与杠杆不垂直时,力臂与杠杆不重合。力臂包含了力的作用点和力的方向两个要素。
杠杆可以是直的,也可以是弯的。即杠杆可以是各种各样的形状。
支点一定在杠杆上。动力和阻力可以在支点两侧,也可在支点同侧。作用在杠杆上的动力和阻力使杠杆转动的方向一定是相反的,但动力和阻力的方向不一定相反。
F1的力臂l1
不在杠杆上。
4. 画力臂的要求
从支点O向力的作用线引垂线,画出垂足,则从支点到垂线的距离就是力臂。
过力的作用点沿力的方向画出力的作用线。
注意: 必要时要用虚线将力的作用线延长。
先确定杠杆的支点O和动力、阻力的方向。
最后用大括号或箭头勾出力臂,并在旁边写上字母l1或l2。
动力臂l1
5. 力臂的画法
阻力F2
动力F1
阻力臂l2
以人用撬棒翘起物体为例——画出动力F1与阻力F2的力臂
支点O
力的
作用线
F1
F2
视频欣赏——《杠杆与杠杆的五要素》
【例题1】关于杠杆,下列说法中正确的是( )
A. 杠杆一定是一根直的硬棒
B. 杠杆的支点一定在杠杆上,且在杠杆的中间位置
C. 力臂可能在杠杆上,也可能不在杠杆上
D. 从支点到动力作用点的距离叫动力臂
杠杆是一根硬棒,但不一定是直的,杠杆的支点一定在杠杆上,不一定在杠杆的中间位置,所以A、B选项是错误的。
力臂可能在杠杆上,也可能不在杠杆上,选项C正确;
D选项中,从支点到动力作用线的距离叫动力臂,所以 D选项错误。
???C
故选C。
画力F1的力臂时,只需过支点O做F1的垂线即可;
因为L2是F2的力臂,所以画出与L2垂直的线段,就是力的作用线,
再根据动力与阻力对杠杆的作用效果相反,即可确定阻力F2的方向。
【例题2】如图所示杠杆在力F1、F2的作用下处于静止状态,L2是F2的力臂。请在图中画出力F1的力臂L1以及阻力F2.
F2
l1
∟
【例题3】如图开瓶器开启瓶盖时可抽象为一杠杆,不计自重。选项图能正确表示它工作示意图的是( )
由题图知,向上用力时,起子围绕左端O转动,因此O为支点。又因为动力F1的方向向上,使杠杆沿逆时针转动,所以阻力F2的方向向下,使杠杆沿顺时针转动。故选B。
???B
①为什么体重不同的两人
能让跷跷板水平静止?
在杠杆的使用中,杠杠的平衡状态是一种非常重要的状态。
杠杆满足什么条件时才会平衡呢?下面我们一起探究。
②为什么重力相同的两人
不能让跷跷板水平静止?
1. 杠杆的平衡:
杠杆静止或匀速转动,就说杠杆处于平衡状态。
提出问题
猜想与假设
杠杆平衡时,动力、动力臂、阻力、阻力臂之间存在着怎样的关系?
动力+动力臂=阻力+阻力臂
动力-动力臂=阻力-阻力臂
动力×动力臂=阻力×阻力臂
动力:动力臂=阻力:阻力臂
…………
探究杠杆的平衡条件
学生实验
①实验器材:杠杆、钩码、铁架台、弹簧测力计。
②测量的物理量:力、力臂。
③当杠杆平衡时,分别测出动力F1、阻力F2,动力臂L1、阻力臂L2。并多次改变力和力臂的大小,获取多组数据。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}实验
次数
动力F1/N
动力臂l1/cm
阻力
F2/N
阻力臂l2/cm
1
2
3
设计实验
实验表格
①把杠杆安装在支架上,调节杠杆两端的平衡螺母, 使杠杆在水平位置平衡。
平衡螺母
使杠杆在水平位置平衡时,两个力臂可以直接从杠杆上直接读出,就不用测量了,非常方便。
另外,可以消除杠杆自身的重力对实验结果的影响。
杠杆哪端高,就把平衡螺母向哪端调节;或者杠杆向哪边偏,就把平衡螺母向反方向调节
平衡螺母
实验步骤
②在杠杆两边挂不同数量的钩码,把支点右边的钩码对杠杆的作用力当作动力F1,支点左边的钩码对杠杆的作用力当作阻力F2。
调节钩码的位置,使杠杆在水平位置重新平衡,将动力F1、阻力F2、动力臂L1、阻力臂L2的实验数据填入表中。
实验中所用每个钩码的重力都相等。
③改变阻力和阻力臂的大小,相应调节动力和动力臂的大小,使杠杆在水平位置重新平衡,再做几次实验。
④在杠杆的一侧挂上钩码作为阻力,通过在其他位置上用弹簧测力计拉住杠杆的办法使杠杆平衡。
将动力F1、阻力F2、动力臂l1、阻力臂l2记录在表格中。
注意:
弹簧测力计只有沿竖直方向施加力,才可以直接读出力臂。
F1
o
l1
实验数据记录
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}实验次数
动力F1/N
动力臂l1/cm
阻力F2/N
阻力臂l2/cm
1
2
10
1
20
2
3
10
2
15
3
4
5
1
20
交流与小结
动力×动力臂=阻力×阻力臂,
杠杆平衡时
分析表中的数据,找出它们之间的关系,你从中有什么发现?
杠杆平衡时:动力×动力臂=阻力×阻力臂
计算公式:
F1 L1=F2 L2
注意:
①应用公式计算时,单位要统一,即动力和阻力的单位要用牛(N),动力臂和阻力臂的单位要相同。
②杠杆是否平衡,取决于力和力臂的乘积;乘积相等就平衡;否则沿着乘积大的那端转动。
或变形式:
作用在杠杆上两个力的大小
与他们的力臂成反比。
这就是阿基米德
发现的杠杆原理。
????1????2=????1????2
?
2. 杠杆的平衡条件
①让杠杆在水平位置静止的目的是:
一是使杠杆的重心在支点,以消除杠杆自身重力对实验的影响。二是便于直接读出力臂。
②多次测量获得多组实验数据的目的是:
避免偶然性,获得普遍性的结论。
【评估与交流】
③在实验前要调节杠杆两端的平衡螺母,使杠杆水平平衡。挂钩码后,不能再调节平衡螺母。
④读数时,杠杆仍要保持处于水平平衡状态,以便直接读出力臂的长度。
调节
平衡螺母
不能调节
平衡螺母
(b)
(a)
l2
∟
⑤弹簧测力计一定沿竖直方向施加力。
如图(a)所示,弹簧测力计沿竖直方向施加力时,力臂l1是10cm。如果弹簧测力计不沿竖直方向施加力, 如图(b)所示,则力臂为l2,
l2 < l1,将小于10cm,变小。
l1
视频演示《实验—探究杠杆的平衡条件》
【例题4】如图所示,小明利用铁架台、带有刻度的杠杆、细线、弹簧测力计、若干钩码(每个钩码重均为0.5N)等实验器材,探究杠杆的平衡条件。
①实验前,杠杆静止在甲所示的位置,则此时杠杆处于 ??(选填“平衡”或“不平衡”)状态;要使杠杆在水平位置平衡,应将平衡螺母向 调节,这样做的目的是消除杠杆自重对实验的影响。
②将杠杆调整好后,如图乙所示,在A点挂3个钩码,则应在B点挂 个钩码,才能使杠杆在水平位置平衡。
③如图丙所示,小明用弹簧测力计替代钩码,先在B点竖直向下拉使杠杆平衡,然后将弹簧测力计逐渐向右倾斜,要使杠杆仍然在水平位置平衡,则弹簧测力计的示数将逐渐_______(选填“变大”或“变小”),原因是__________。
④在实验中,改变力和力臂的大小得到多组数据的目的是:
_____(填序号)。
A. 使测量数据更准确
B. 多次测量取平均值减小误差
C. 避免偶然性,使实验结论具有普遍性
解析见下页
①实验前,杠杆静止在图甲所示的位置,则此时杠杆处于 ?(选填“平衡”或“不平衡”)状态;要使杠杆在水平位置平衡,应将平衡螺母向 调节,这样做的目的是消除杠杆自重对实验的影响。
②将杠杆调整好后,如图乙所示,在A点挂3个钩码,则应在B点挂 个钩码,才能使杠杆在水平位置平衡。
①杠杆静止在图甲位置,此时处于平衡状态;调节杠杆在水平位置平衡,杠杆的左端上翘,平衡螺母向上翘的左端移动。
②由杠杆平衡条件F1l1=F2l2得3G1×2l=nG1×3l,n=2,故在B点挂2个钩码。
平衡
左
2
③如图丙所示,小明用弹簧测力计替代钩码,先在B点竖直向下拉使杠杆平衡,然后将弹簧测力计逐渐向右倾斜,要使杠杆仍然在水平位置平衡,则弹簧测力计的示数将逐渐_______(选填“变大”或“变小”),原因是_________________。
④在实验中,改变力和力臂的大小得到多组数据
的目的是:_____(填序号)。
A.使测量数据更准确
B.多次测量取平均值减小误差
C.避免偶然性,使实验结论具有普遍性
③当拉力F向右倾斜时,力臂变小,要保持杠杆仍在水平位置平衡,根据杠杆的平衡条件,因阻力和阻力臂不变,则拉力F将变大。
④实验测多组数据的目的是使得出的结论更具有普遍性,故选C。
变大
拉力力臂变小
C
①如图所示,是利用撬棒撬石头时的情景,请仔细观察,它的动力臂和阻力臂,哪个更长呢?
我们在使用时,是省力?还是费力呢?
②如图所示,是利用食品夹时的情景,请仔细观察,它的动力臂和阻力臂,哪个更长呢?
根据杠杆的平衡条件对杠杆进行分析:
>
省力杠杆
等臂杠杆
费力杠杆
=
<
提示:判断杠杆的类型,实际就是比较动力臂和阻力臂的大小。
如图所示,人的动力为F1 ,动力臂为l1 ;阻力为F2,阻力臂为l2。
若l1<l2,则F1 F2
若l1= l2,则F1 F2
若l1>l2,则F1 F2
根据杠杆的平衡条件:F1 L1=F2 L2
①特点:动力臂大于阻力臂,省力费距离。
o
F1
F2
使用省力杠杆时,动力移动的距离A0A大于阻力移动的距离BB0,即费距离。
因为l1>l2,所以F1 <F2,即省力。
根据杠杆的平衡条件:F1 L1=F2 L2
1. 省力杠杆
②省力杠杆的实例分析
F1
F2
o
o
F2
F1
剪刀相当于两个杠杆组合在一起
l2
l1
因为l1>l2,所以F1<F2,即省力。
③生活中的一些省力杠杆:
o
F1
F2
使用费力杠杆时,动力移动的距离h1小于阻力移动的距离h2,即省距离。
F1
F2
h2
h1
因为l1<l2,所以F1 >F2,即费力。
根据杠杆的平衡条件:F1 L1=F2 L2
①特点:动力臂小于阻力臂,费力省距离。
o
2. 费力杠杆
②费力杠杆的实例分析
o
F1
F2
F2
l1
l2
l2
l1
筷子相当于两个杠杆组合在一起。
人的右手与钓鱼竿接触处O为支点。
o
F1
因为l1<l2,所以F1 >F2,即费力。
③生活中的一些费力杠杆
扫把
镊子
船桨
①特点:动力臂等于阻力臂,动力等于阻力,不费距离不省距离。
o
F1
F2
使用等臂杠杆时,动力移动的距离等于阻力移动的距离,即不省距离也不费距离。
因为l1=l2,所以F1=F2 ,即动力等于阻力。
根据杠杆的平衡条件:F1 L1=F2 L2
3. 等臂杠杆
②生活中的等臂杠杆
定滑轮
托盘天平
跷跷板
杠杆分类
力臂关系
省费力、距离情况
应用举例
省力杠杆
费力杠杆
等臂杠杆
省力费距离
省距离费力
不省力也不省距离
撬棍、扳手、钢丝钳
天平、跷跷板
镊子、鱼竿、筷子
l动>l阻
l动<l阻
l动=l阻
4. 总结:杠杠的分类
【例题6】在如图所示的工具中,使用时属于费力杠杆的是( )
B
A.支点在起子与瓶盖中间接触处,动力臂大于阻力臂,是省力杠杆;
B.支点在夹子两壁连接处,动力臂小于阻力臂,是费力杠杆;
C.支点是锤子与地面的接触点,动力臂大于阻力臂,是省力杠杆;
D.支点在夹子两壁连接处,动力臂大于阻力臂,是省力杠杆。
B是费力杠杆,所以选B。
A.瓶盖起子 B.食品夹 C.起钉锤 D.核桃夹
生活?物理?社会
生活中的剪刀
剪刀是生活中常见的工具,它也是一种杠杆。你是否注意到,从事不同行业的人所用的剪刀各有特点?
栽衣剪刀 理发剪刀 剪铁皮剪刀 修枝剪刀
根据杠杆的平衡条件:
F1 L1=F2 L2
人所用的力:F1 = ????2????1 F2
?
结论:当阻力不变时,被剪物体离支点越近,阻力臂L2越小,动力F1越小(越省力)。
生活?物理?社会
生活中的剪刀
栽缝用的剪刀刀刃比平常家用剪刀的刀刃长得多,完成一次剪裁动作可以裁剪较长的布料。
理发师用的剪刀手柄比较短,他们剪发时手的动作幅度较小,可提高剪发的频率。
剪铁皮的剪刀,其动力臂比阻力臂长,是省力杠杆,只要用较小的力,就能把坚硬的金属片剪开。
生活?物理?社会
生活中的剪刀
园艺师使用的剪刀有很多种,如修整冬青树的势刀、剪花枝的剪刀等,它们各有特点。请你调查一下,园艺师使用了哪些剪刀?它们各有什么特点?为什么这样设计?
粗枝剪
能剪切0-4cm的粗枝,类似老虎钳子。实际上是个省力杠杆。
园艺大剪刀
刀刃比平常剪刀的刀刃长得多,完成一次剪裁动作可以裁剪较多的枝叶。
【例题5】在苏州动物园内,一位物理老师利用杠杆原理,仅用小小的弹簧测力计就测出了一头大象的质量(如图甲)。测量时用了一根长度为12m的槽钢作为杠杆(如下图乙所示),吊钩固定于槽钢的中点O。当槽钢水平静止时,弹簧测力计的示数F1=200N,测得l1为6m,l2为4cm。不计铁笼的质量,请估算大象的质量。 g取10 N/kg 。
甲
乙
L2=4cm=0.04m
由F1l1=F2l2 得:
F2=????1????1????2=200N×6m0.04m=3×104N
即大象的重力G为3×104N
则大象的质量m为
m=????????=3×104N10N/kg
= 3×103kg
?
生活?物理?社会
人体中的杠杆
骨骼、肌肉和关节构成了人体的运动系统,尽管人体的各种运动相当复杂,但最基本的运动都是由骨骼绕关节转动产生的,其模型就是杠杆。例如,当手握哑铃向上运动时,上臂中的肱三头肌伸展、肱二头肌收缩产生的力使前臂骨骼绕肘关节转动。在这里,前臂骨骼可以看成杠杆,肘关节是支点,哑铃对手的压力是阻力,上臂中的肌肉对前臂骨骼施加的力则是动力。
生活?物理?社会
人体中的杠杆
动力臂l1
阻力F2
阻力臂l2
支点O
动力F1
前臂骨骼实质是一个费力杠杆。
因为 l1<l2,
所以 F1> F2
根据杠杆的平衡条件:
F1 L1=F2 L2
生活?物理?社会
人体中的杠杆
如图所示,当手托住铁球并绕腕关节向上转动时,手就是一个杠杆,铁球压在掌心上的力是阻力,腕关节是支点,前臂中的伸肌伸展和屈肌收缩产生动力,使托住铁球的手向上转动.
人体有600多块肌肉,它们在神经系统的控制下,分别负责各部位的运动。当你做抬腿、伸臂、点头、叩齿等动作时,你就用到了身上各种各样的杠杆。
人体中的杠杆为科技工作者的创造和发明提供了很多启示,机器人和国际空间站上的机械臂(p.29)的发明就是其生动的体现。
生活?物理?社会
人体中的杠杆
如图所示,当手托住铁球并绕腕关节向上转动时,手就是一个杠杆,铁球压在掌心上的力是阻力,腕关节是支点,前臂中的伸肌伸展和屈肌收缩产生动力,使托住铁球的手向上转动.
阻力F2
支点O
动力F1
阻力臂l2
前臂骨骼实质是一个费力杠杆。
因为 l1<l2,
所以 F1> F2
根据杠杆的平衡条件:
F1 L1=F2 L2
动力臂l1
3
课堂总结
三类杠杆
力臂关系
省费力、距离情况
应用举例
省力杠杆
l动 l阻
费力杠杆
l动 l阻
等臂杠杆
l动 l阻
②杠杆的五要素:支点、动力、动力臂、阻力、阻力臂。
①杠杆的定义:在力的作用下可绕一固定点转动的硬棒称为杠杆。
③杠杆的平衡条件:动力?动力臂=阻力?阻力臂
F1l1=F2l2
④杠杆分类
杠杆
>
<
=
省力费距离
省距离费力
不省力也不省距离
撬棍、扳手、钢丝钳
天平、跷跷板
镊子、鱼竿、筷子
4
WHAT?WHY?WOW
1. 指出图中各种杠杆工作时的支点、动力、动力臂、阻力和阻力臂,并说明这些杠杆中哪些是省力的,哪些是费力的。
F1
F2
o
l2
F2
o
l2
F1
l1
F2
o
l2
F1
省力杠杆
费力杠杆
省力杠杆
2. 在“探究杠杆的平衡条件“实验中,我们也可用在杠杆支点的两边分别挂钩码的方法,来探究杠杆的平衡条件。如图所示,在杠杆的左边距支点20cm处挂了四个钩码,要使杠杆在水平位置平衡,如何在杠杆的右边挂钩码?(钩码的质量相等)
根据杠杆的平衡条件:
F1 L1=F2 L2
m1 gL1= m2 gL2
m1 L1= m2 L2
若 L2= L1 则 m2 = m1
若 L2=0.5 L1 则m2 =2 m1
所以可在右边20cm处挂4个钩码,或在10cm处挂8个钩码。
3. 小制作:蜡烛跷跷板。
将一支蜡烛的两端削尖,在中间垂直插入一枚大号缝衣针,把缝衣针的两端分别放在两个玻璃杯上,就做成了一个蜡烛跷跷板。用小刀对蜡烛的两端进行加工,使跷跷板能在水平位置平衡。点燃蜡烛的两端,蜡烛跷跷板会怎样运动?你能说明其中的道理吗?
因为缝衣针不可能正好插在蜡烛的重心位置,质量略大的一端向下倾斜,火苗向上烧,使蜡烛的这一端熔化较快,质量很快小于另一端,从而向上翘起(另一端就会下倾);同理,当另一端质量变小后又向上翘起……蜡烛跷跷板就这样不停地往复摆动。
5
课堂练习
1. 如图所示,请画出作用在杠杆B端上最小的动力F1和阻力F2的力臂l2.
F1
∟
l2
∟
作图步骤:
①确定最大力臂:作用在B端上动力F1最小时,则动力臂最大,应该为OB。
②画力的作用线:过B点做与OB垂直的线段(即动力的作用线)。
③确定动力的方向:与阻力F2的作用效果相反,应该向上。
人的右手与鱼竿接触点为支点,左手的力为动力F1,鱼对鱼竿末端的拉力F2为阻力。如图所示。
2. 如图是使用钓鱼竿的示意图,O为支点,F1是手对竿的作用力,F2是鱼线对竿的作用力,请在图中画出F1、F2的力臂。
3.图中杠杆质地均匀,每个钩码重0.5 N,下列操作中可以使杠杆在水平位置平衡的是(杠杆上有等间隔的刻度)( )
D
使杠杆在水平位置平衡,需满足两个力使杠杆转动的方向相反,所以A与C都不能使杠杆水平平衡。
由杠杆的平衡条件:F1l1=F2l2 计算出D图中2N×3=1N×6,所以可以使杠杆平衡。
4. 如图为工地搬运砖头的独轮车,人抬起车把时,车体可以看成个杠杆,关于这个杠杆下列说法正确的是( )
A.手握的位置靠近把手末端时更费力
B.砖头的位置远离车轮时抬起更省力
C.轮子的中心是杠杆的支点
D.图中拉力F大于重力G
A.手握的位置靠近把手末端时,动力臂更长,则更省力,故A错误;
B.砖头的位置远离车轮时,重力的阻力臂变大,故抬起更费力,故B错误;
C.工地搬运砖头的独轮车工作时,车轮中心是支点,故C正确;
D.根据杠杆平衡条件,拉力力臂大于阻力力臂时省力,图中拉力F小于重力G,故D错误。所以选C。
C
5. 如图3所示,O为轻质杠杆AB的支点,B点挂一重物G,若在B点施加F1、或在A点分别施加F2、F3、F4四个力后,杠杆均保持水平位置平衡,则这四个力中最小的力是( )
由图可知,O为支点,力F1与杠杆垂直,则力F1对应的动力臂为OB;力F3与杠杆垂直,则力F3对应的动力臂为OA;
由图可知,F2、F4对应的力臂都小于OA,而OB>OA,所以OB是最大的力臂;
由杠杆平衡条件F1l1=F2l2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小;因为F1对应的动力臂最长,所以F1最小。
故A符合题意,选项B、C、D不符合题意。
A
6. 撬棒是人们在劳动中应用杠杆原理的工具。如图所示是工人利用撬棒撬动大石头的情景,撬棒上O点为杠杆的支点。下列分析正确的是( )
B
A.此时撬棒为等臂杠杆
B.应用此撬棒的主要目的是省力
C.力F的作用点靠近O点会更省力
D.应用此撬棒的主要目的是省距离
ABD选项:由图知,在使用撬棒时,动力臂大于阻力臂,为省力杠杆,使用该杠杆省力但费距离,故B正确、AD错误;
C选项:力F的作用点靠近O点时,动力臂减小,而阻力、阻力臂不变,由杠杆平衡条件可知动力会变大,会更费力,故C错误。
7. 如图4所示为等刻度的轻质杠杆,在A处挂一个重为2牛的物体,若要使杠杆在水平位置平衡,则在B处施加的力( )
解析 子弹在枪膛中受火药爆炸后产生气体的作用力而运动的距离为
枪膛长度,即s=50 cm=0.5 m,子弹离开枪膛后就不再受火药爆炸产生的
气体推力,气体推力不再做功;所以,气体对子弹做功:W=Fs=700 N×0.5 m
=350 J。
设杠杆每一格长度是a,当B处的作用力与杠杆垂直向下时,
力臂最大,此时作用力最小,由杠杆平衡条件可得
FAlA=FB最小lB 即 2N×2L=FB最小×4a 解得 FB最小=1N
当作用在B处的力与杠杆不垂直时,力臂小于4a,作用力大于1N,因此要使杠杆平衡,作用在B处的力F ≥1N,故A符合题意. 选A。
A. 可能是2牛 B. 可能是0.5牛 C. 一定是1牛 D. 一定是4牛
A
8. 如图所示,采石场的工人想用撬棒撬起一块大石头,甲工人说按住撬棒向下施力最省力;乙工人说抬着撬棒向上施力最省力。请你分别作出这两种不同施力方向的最小作用力的示意图,并说明哪种施力方向最省力。(已知C到O1的距离与C到O2的距离相等)
8. 请你分别作出这两种不同施力方向的最小作用力的示意图,并说明哪种施力方向最省力。(已知C到O1的距离与C到O2的距离相等)
两种方法中,最小作用力的示意图如图甲、乙所示;图甲中,O1是支点,动力F甲的力臂为AO1的长;图乙中, O2是支点,动力F乙的力臂为AO2的长。
设石头对杠杆的压力为F压,由杠杆平衡条件知: F甲×AO1=F压×CO1,
F乙×AO2=F压×CO2, ∵ CO1=CO2,AO1
乙
甲
杠杆的B点挂重物,在A端通过细绳施加竖直向上、大小为 10牛的拉力F使杠杆水平平衡时,由杠杆平衡条件F1L1 = F2L2可知,
10牛×OA = G×OB 0A :OB= G:10N ………①
如果把重物悬挂点和拉力作用点互换,此时杠杆平衡时,
F1'OB = G×OA 22.5N×0B = G×OA ………②
由①与②得 G?=225 G=15N 所以选B。
9. 如图所示,轻质杠杆OA可绕O点转动。在杠杆的B点挂上重物,在A端通过细绳施加竖直向上10牛的拉力F使杠杆水平平衡。如果把重物悬挂点和拉力作用点互换,当杠杆水平平衡时,竖直向上的拉力大小变为22. 5牛。则该物体的重为( )
A. 12牛 B. 15牛 C. 18牛 D. 21牛
B
10. 如图,轻质均匀杠杆OB长1m,能绕支点O转动,B端用细绳BC竖直悬于C点,有一重力为200N的物块挂在A点,OA长0.3m,求:
①此时绳BC对杠杆的拉力F的大小。
②若绳BC能承受的最大拉力为150N,移动重物到某一位置,绳BC恰好断裂,求重物悬挂点到支点O的距离。
①根据杠杆的平衡条件得 F1l1=F2l2 得:F×OB=G×OA,即
F×1 m=200 N×0.3 m,则 F=60 N
②设重物悬挂点到支点O的距离为L,绳BC恰好断裂,此时最大拉力F′=150 N,根据杠杆的平衡条件得F′×BO=G×L,即150N×1m=200N×L,
则L=0.75 m。即重物悬挂点到支点O的距离为0.75m时,绳BC恰好断裂。
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
