北京人大附中丰台学校2023~2024学年第二学期初三开学考数学试卷(pdf、无答案)
文档属性
| 名称 | 北京人大附中丰台学校2023~2024学年第二学期初三开学考数学试卷(pdf、无答案) |  | |
| 格式 | |||
| 文件大小 | 552.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 20:06:38 | ||
图片预览



文档简介
2023-2024 学年度第二学期初三年级开学作业验收练习 1
数 学
2024.2
考 1. 本验收共三道大题 28小题,共 8页,满分 100分。验收时间 120分钟。
2. 在试卷和答题卡上准确填写姓名、学号。
生
3. 试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
须
4. 在答题卡上,选择题、作图题用 2B铅笔作答,其他试题用黑色字迹签字笔作
知 答。
5. 验收结束,将答题卡交回。
一、 单选题(每小题 2 分,共 16 分)
1.故宫又称紫禁城,位于北京中轴线的中心,占地面积高达720000平方米,在世界宫殿建
筑群中面最大.请将720000用科学记数法表示应为( )
A.0.72 × 105 B.7.2 × 105 C.7.2 × 104 D.72 × 103
2.下列图形中,是轴对称图形不是中心对称图形的是( )
A. B. C. D.
3. 若实数 a,b,c,d 在数轴上的对应点的位置如图所示,则正确的结论是( )
A.|a|<4 B.b+d>0 C.ac>0 D.a﹣c>0
4.已知抛物线 y=a(x﹣2)2+k(a>0,a,k 为常数),A(﹣3,y1),B(3,y2),C(4,
y3)是抛物线上三点,则 y1,y2,y3由小到大依序排列为( )
A.y2<y3<y1 B.y2<y1<y3 C.y1<y2<y3 D.y3<y2<y1
2 1
5.如果 y = x +3,且 ≠ ,那么代数式 2 2 + 的值为( )
1 1
A. B. C. 3 D.3
3 3
1 1
6.用三个不等式 a b, > 0, < 中的两个不等式作为题设,余下的一个不等式作为结
论组成一个命题,组成真命题的个数为( )
A.0 B.1 C.2 D.3
1 / 8
7.已知:在四边形 中, ∥ ,∠ = 90°,点 是线段 上一
点,且 平分∠ , 平分∠ ,给出下面四个结论:① ⊥ ;
②∠ = ∠ ;③ AB CD = BE EC ;④ = 上述结
论中,所有正确结论的序号是( )
A.①② B.③ C.①②③ D.①②③④
8.如果一个圆的内接三角形有一边的长度等于半径,那么称其为该圆的“半径三角形”.给出下
面四个结论:
①一个圆的“半径三角形”有无数个;
②一个圆的“半径三角形”可能是锐角三角形、直角三角形或钝角三角形;
③当一个圆的“半径三角形”为等腰三角形时,它的顶角可能是30 或120 ;
④若一个圆的半径为 2,则它的“半径三角形”面积最大值为2 + √3.
上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.①②③ D.①②④
二、 填空题(每小题 2 分,共 16 分)
9.若√1 在实数范围内有意义,则实数 的取值范围是 .
10. 因式分解 2 + 2 + = .
11.如图,点 A,B,C 是⊙ 上的三点.若∠ 90°,∠ = 30°,则∠ 的度数
为 .
12. 如图,在平行四边形 中,E 为 的中点, , 交于点 F,则△ 和△
的面积比为 .
13.把图 1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成
如图 2,图 3所示的正方形,则图 1中菱形的边长为 .
第 11题图 第 12题图 第 13题图
14. 已知,点 A,B,C 在⊙O 上,∠ABC 110°.若点 D 为⊙O 上一点(不与点 A,C 重合),则
∠ADC 的度数为___________.
15. 如图,点 M 在正六边形的边 EF 上运动. 若 ABM = x ,写出一
个符合条件的 x 的值 .
2 / 8
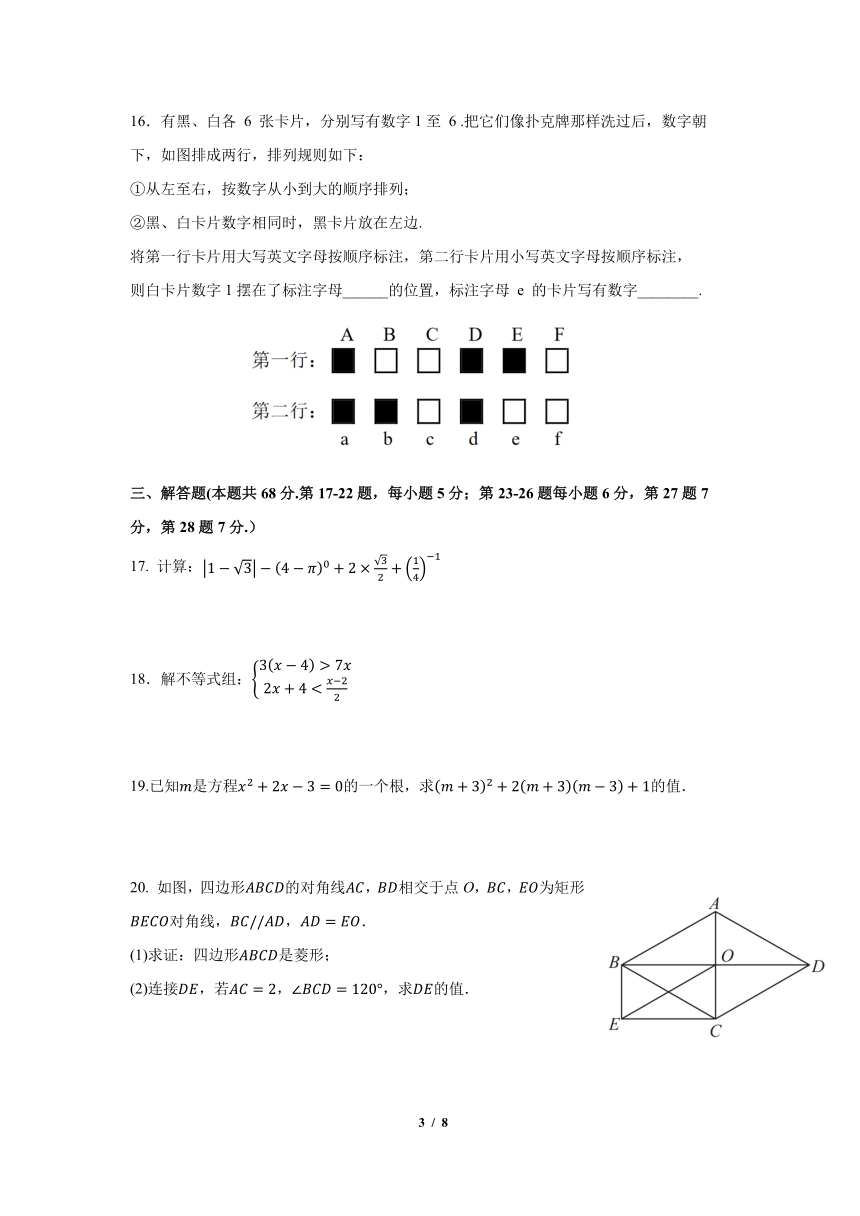
16.有黑、白各 6 张卡片,分别写有数字 1至 6 .把它们像扑克牌那样洗过后,数字朝
下,如图排成两行,排列规则如下:
①从左至右,按数字从小到大的顺序排列;
②黑、白卡片数字相同时,黑卡片放在左边.
将第一行卡片用大写英文字母按顺序标注,第二行卡片用小写英文字母按顺序标注,
则白卡片数字 1摆在了标注字母______的位置,标注字母 e 的卡片写有数字________.
三、解答题(本题共 68 分.第 17-22 题,每小题 5 分;第 23-26 题每小题 6 分,第 27 题 7
分,第 28 题 7 分.)
计算: √3 1
1
17. |1 √3| (4 )0 + 2 × + ( )
2 4
3( 4) > 7
18.解不等式组:{ 2
2 + 4 <
2
19.已知 是方程 2 + 2 3 = 0的一个根,求( + 3)2 + 2( + 3)( 3) + 1的值.
20. 如图,四边形 的对角线 , 相交于点 O, , 为矩形
对角线, // , = .
(1)求证:四边形 是菱形;
(2)连接 ,若 = 2,∠ = 120°,求 的值.
3 / 8
21. 如图,在长为30m、宽20m的矩形空地上,修建一横一纵两条道路,并且横、纵两条
道路的宽度比为 2 : 3,余下的部分作为草坪,若草坪面积为486m2,求两条道路的宽度各是
多少?
22. 在平面直角坐标系中,一次函数 = + ( ≠ 0)的图象平行于直线 = 2 ,且经过
点 (1,2).
(1)求这个一次函数的表达式;
(2)当 < 1时,对于 的每一个值,一次函数 = + ( ≠ 0)的值都大于一次函数
= + 1的值,直接写出 的取值范围.
23. 2022年10月12日,“天宫课堂”第三课在中国空间站的问天实验舱开讲,“太空教师”陈
冬、刘洋、蔡旭哲为广大青少年带来一场精彩的太空科普课.为了激发学生的航天兴趣,
弘扬科学精神,某校甲、乙两个校区的八年级所有学生(两个校区八年级各有200 名学
生)参加了“格物致知 叩问苍穹”为主题的太空科普知识竞赛.为了解八年级学生的太空科
普知识掌握情况,从每个校区八年级的科技小组中分别随机抽取了20名学生的竞赛成绩,
并整理成部分信息如下:
a.乙校区学生成绩的频数分布直方图如下(数据分为 5组:65 x 80;80 x 85;
85 x 90;90 x 95;95 x 100 ):
4 / 8
b.乙校区的学生成绩数据在90 x 95这一组的是:
91 91 92 94
c.两个校区学生成绩的平均数、中位数、方差如下表所示:
校区 平均数 中位数 方差
甲校区 89.3 88.5 42.6
乙校区 89.3 m 87.2
根据上述信息,解答问题:
(1)m = ______;
(2)对于抽取的八年级学生竞赛成绩,高于本校区平均分的人数更多的是______校区,成绩
更整齐的是______校区(填“甲”或“乙”);
(3)抽样调查中,两个校区共有 30%的学生竞赛成绩不低于 95分.该校计划从两个校区选
派成绩不低于 95分的学生参加全区的竞赛,估计参赛的八年级学生中,甲校区有______人
被选中.
24. 如图,在△ 中, = ,以 为直径的⊙ 分别交 , 于点 , ,过点 作∠
1
使得∠ = ∠ ,交 的延长线于点 .
2
(1)求证: 是⊙ 的切线;
(2)若 BD = 2,CE = 5 ,求 的长.
5 / 8
1
25.给定一个函数: y = x + +1(x 0),为了研究它的图象与性质,并运用它的图象与性
x
质解决实际问题,进行如下探索:
(1)图象初探
①列表如下
1 1 1
x …… 1 2 3 4 ……
4 3 2
21 13 7 21
y …… m 3 n ……
4 3 2 4
请直接写出 m,n 的值;
②请在如下的平面直角坐标系中描出剩余两点,并用平滑的曲线画出该函数的图象.
(2)性质再探
请结合函数的图象,写出当 x =__________,y 有最小值为__________;
(3)学以致用
某农户要建进一个如图①所示的长方体无盖水池,其底面积为 1平方米,深为 1米.已知
底面造价为 3千元/平方米,侧面造价为 0.5千元/平方米.
设水池底面一边长为 x 米,水池总造价为 y 千元,可得到 y 与 x 的函数关系式为:
1
y = x + + 3.根据以上信息,请回答以下问题:
x
① 水池总造价的最低费用为_____________千元;
②若该农户预算不超过 5.5千元,请直接写出 x 的值应控制在什么范围?
________________
6 / 8
26.在平面直角坐标系 xOy 中,点 A( 3, y B1 ), (a +1, y
2
2 )在抛物线 y = x 2ax +1上.
(1)当 a = 2时,求抛物线的顶点坐标,并直接写出 y1和 y2 的大小关系;
(2)抛物线经过点C (m, y3 ).
①当m = 4 时,若 y1 = y3 ,则 a 的值为_______;
②若对于任意的4 m 6都满足 y1 y3 y2 ,求 a 的取值范围.
27.如图,正方形 ABCD中,点 E,F 分别在BC,CD上,BE =CF, AE, BF 交于点 G.
(1)求 AGF 的度数;
(2)在线段 AG上截取MG = BG ,连接DM , AGF 的角平分线交DM 于点 N.
①依题意补全图形;
②用等式表示线段MN 与 ND的数量关系,并证明.
7 / 8
28.在平面直角坐标系 xOy 中,对于点P (x1, y1 ),给出如下定义:当点Q (x2 , y2 )满足
x1 + x2 = y1 + y2时,称点 Q 是点 P 的等和点.已知点P (2,0).
(1)在Q1 (0,2),Q2 ( 2, 1),Q3 (1,3)中,点 P 的等和点有______;
(2)点 A 在直线 y = x + 4上,若点 P 的等和点也是点 A 的等和点,求点 A 的坐标;
(3)已知点B (b,0)和线段 MN,对于所有满足 BC =1的点 C,线段 MN 上总存在线段 PC 上每
个点的等和点.若 MN 的最小值为 5,直接写出 b 的值.
8 / 8
数 学
2024.2
考 1. 本验收共三道大题 28小题,共 8页,满分 100分。验收时间 120分钟。
2. 在试卷和答题卡上准确填写姓名、学号。
生
3. 试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
须
4. 在答题卡上,选择题、作图题用 2B铅笔作答,其他试题用黑色字迹签字笔作
知 答。
5. 验收结束,将答题卡交回。
一、 单选题(每小题 2 分,共 16 分)
1.故宫又称紫禁城,位于北京中轴线的中心,占地面积高达720000平方米,在世界宫殿建
筑群中面最大.请将720000用科学记数法表示应为( )
A.0.72 × 105 B.7.2 × 105 C.7.2 × 104 D.72 × 103
2.下列图形中,是轴对称图形不是中心对称图形的是( )
A. B. C. D.
3. 若实数 a,b,c,d 在数轴上的对应点的位置如图所示,则正确的结论是( )
A.|a|<4 B.b+d>0 C.ac>0 D.a﹣c>0
4.已知抛物线 y=a(x﹣2)2+k(a>0,a,k 为常数),A(﹣3,y1),B(3,y2),C(4,
y3)是抛物线上三点,则 y1,y2,y3由小到大依序排列为( )
A.y2<y3<y1 B.y2<y1<y3 C.y1<y2<y3 D.y3<y2<y1
2 1
5.如果 y = x +3,且 ≠ ,那么代数式 2 2 + 的值为( )
1 1
A. B. C. 3 D.3
3 3
1 1
6.用三个不等式 a b, > 0, < 中的两个不等式作为题设,余下的一个不等式作为结
论组成一个命题,组成真命题的个数为( )
A.0 B.1 C.2 D.3
1 / 8
7.已知:在四边形 中, ∥ ,∠ = 90°,点 是线段 上一
点,且 平分∠ , 平分∠ ,给出下面四个结论:① ⊥ ;
②∠ = ∠ ;③ AB CD = BE EC ;④ = 上述结
论中,所有正确结论的序号是( )
A.①② B.③ C.①②③ D.①②③④
8.如果一个圆的内接三角形有一边的长度等于半径,那么称其为该圆的“半径三角形”.给出下
面四个结论:
①一个圆的“半径三角形”有无数个;
②一个圆的“半径三角形”可能是锐角三角形、直角三角形或钝角三角形;
③当一个圆的“半径三角形”为等腰三角形时,它的顶角可能是30 或120 ;
④若一个圆的半径为 2,则它的“半径三角形”面积最大值为2 + √3.
上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.①②③ D.①②④
二、 填空题(每小题 2 分,共 16 分)
9.若√1 在实数范围内有意义,则实数 的取值范围是 .
10. 因式分解 2 + 2 + = .
11.如图,点 A,B,C 是⊙ 上的三点.若∠ 90°,∠ = 30°,则∠ 的度数
为 .
12. 如图,在平行四边形 中,E 为 的中点, , 交于点 F,则△ 和△
的面积比为 .
13.把图 1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成
如图 2,图 3所示的正方形,则图 1中菱形的边长为 .
第 11题图 第 12题图 第 13题图
14. 已知,点 A,B,C 在⊙O 上,∠ABC 110°.若点 D 为⊙O 上一点(不与点 A,C 重合),则
∠ADC 的度数为___________.
15. 如图,点 M 在正六边形的边 EF 上运动. 若 ABM = x ,写出一
个符合条件的 x 的值 .
2 / 8
16.有黑、白各 6 张卡片,分别写有数字 1至 6 .把它们像扑克牌那样洗过后,数字朝
下,如图排成两行,排列规则如下:
①从左至右,按数字从小到大的顺序排列;
②黑、白卡片数字相同时,黑卡片放在左边.
将第一行卡片用大写英文字母按顺序标注,第二行卡片用小写英文字母按顺序标注,
则白卡片数字 1摆在了标注字母______的位置,标注字母 e 的卡片写有数字________.
三、解答题(本题共 68 分.第 17-22 题,每小题 5 分;第 23-26 题每小题 6 分,第 27 题 7
分,第 28 题 7 分.)
计算: √3 1
1
17. |1 √3| (4 )0 + 2 × + ( )
2 4
3( 4) > 7
18.解不等式组:{ 2
2 + 4 <
2
19.已知 是方程 2 + 2 3 = 0的一个根,求( + 3)2 + 2( + 3)( 3) + 1的值.
20. 如图,四边形 的对角线 , 相交于点 O, , 为矩形
对角线, // , = .
(1)求证:四边形 是菱形;
(2)连接 ,若 = 2,∠ = 120°,求 的值.
3 / 8
21. 如图,在长为30m、宽20m的矩形空地上,修建一横一纵两条道路,并且横、纵两条
道路的宽度比为 2 : 3,余下的部分作为草坪,若草坪面积为486m2,求两条道路的宽度各是
多少?
22. 在平面直角坐标系中,一次函数 = + ( ≠ 0)的图象平行于直线 = 2 ,且经过
点 (1,2).
(1)求这个一次函数的表达式;
(2)当 < 1时,对于 的每一个值,一次函数 = + ( ≠ 0)的值都大于一次函数
= + 1的值,直接写出 的取值范围.
23. 2022年10月12日,“天宫课堂”第三课在中国空间站的问天实验舱开讲,“太空教师”陈
冬、刘洋、蔡旭哲为广大青少年带来一场精彩的太空科普课.为了激发学生的航天兴趣,
弘扬科学精神,某校甲、乙两个校区的八年级所有学生(两个校区八年级各有200 名学
生)参加了“格物致知 叩问苍穹”为主题的太空科普知识竞赛.为了解八年级学生的太空科
普知识掌握情况,从每个校区八年级的科技小组中分别随机抽取了20名学生的竞赛成绩,
并整理成部分信息如下:
a.乙校区学生成绩的频数分布直方图如下(数据分为 5组:65 x 80;80 x 85;
85 x 90;90 x 95;95 x 100 ):
4 / 8
b.乙校区的学生成绩数据在90 x 95这一组的是:
91 91 92 94
c.两个校区学生成绩的平均数、中位数、方差如下表所示:
校区 平均数 中位数 方差
甲校区 89.3 88.5 42.6
乙校区 89.3 m 87.2
根据上述信息,解答问题:
(1)m = ______;
(2)对于抽取的八年级学生竞赛成绩,高于本校区平均分的人数更多的是______校区,成绩
更整齐的是______校区(填“甲”或“乙”);
(3)抽样调查中,两个校区共有 30%的学生竞赛成绩不低于 95分.该校计划从两个校区选
派成绩不低于 95分的学生参加全区的竞赛,估计参赛的八年级学生中,甲校区有______人
被选中.
24. 如图,在△ 中, = ,以 为直径的⊙ 分别交 , 于点 , ,过点 作∠
1
使得∠ = ∠ ,交 的延长线于点 .
2
(1)求证: 是⊙ 的切线;
(2)若 BD = 2,CE = 5 ,求 的长.
5 / 8
1
25.给定一个函数: y = x + +1(x 0),为了研究它的图象与性质,并运用它的图象与性
x
质解决实际问题,进行如下探索:
(1)图象初探
①列表如下
1 1 1
x …… 1 2 3 4 ……
4 3 2
21 13 7 21
y …… m 3 n ……
4 3 2 4
请直接写出 m,n 的值;
②请在如下的平面直角坐标系中描出剩余两点,并用平滑的曲线画出该函数的图象.
(2)性质再探
请结合函数的图象,写出当 x =__________,y 有最小值为__________;
(3)学以致用
某农户要建进一个如图①所示的长方体无盖水池,其底面积为 1平方米,深为 1米.已知
底面造价为 3千元/平方米,侧面造价为 0.5千元/平方米.
设水池底面一边长为 x 米,水池总造价为 y 千元,可得到 y 与 x 的函数关系式为:
1
y = x + + 3.根据以上信息,请回答以下问题:
x
① 水池总造价的最低费用为_____________千元;
②若该农户预算不超过 5.5千元,请直接写出 x 的值应控制在什么范围?
________________
6 / 8
26.在平面直角坐标系 xOy 中,点 A( 3, y B1 ), (a +1, y
2
2 )在抛物线 y = x 2ax +1上.
(1)当 a = 2时,求抛物线的顶点坐标,并直接写出 y1和 y2 的大小关系;
(2)抛物线经过点C (m, y3 ).
①当m = 4 时,若 y1 = y3 ,则 a 的值为_______;
②若对于任意的4 m 6都满足 y1 y3 y2 ,求 a 的取值范围.
27.如图,正方形 ABCD中,点 E,F 分别在BC,CD上,BE =CF, AE, BF 交于点 G.
(1)求 AGF 的度数;
(2)在线段 AG上截取MG = BG ,连接DM , AGF 的角平分线交DM 于点 N.
①依题意补全图形;
②用等式表示线段MN 与 ND的数量关系,并证明.
7 / 8
28.在平面直角坐标系 xOy 中,对于点P (x1, y1 ),给出如下定义:当点Q (x2 , y2 )满足
x1 + x2 = y1 + y2时,称点 Q 是点 P 的等和点.已知点P (2,0).
(1)在Q1 (0,2),Q2 ( 2, 1),Q3 (1,3)中,点 P 的等和点有______;
(2)点 A 在直线 y = x + 4上,若点 P 的等和点也是点 A 的等和点,求点 A 的坐标;
(3)已知点B (b,0)和线段 MN,对于所有满足 BC =1的点 C,线段 MN 上总存在线段 PC 上每
个点的等和点.若 MN 的最小值为 5,直接写出 b 的值.
8 / 8
同课章节目录
