2023-2024学年数学八年级数据的收集与整理单元测试试题(冀教版)基础卷二含解析
文档属性
| 名称 | 2023-2024学年数学八年级数据的收集与整理单元测试试题(冀教版)基础卷二含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 15:59:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学八年级数据的收集与整理
单元测试 (冀教版) 基础卷二含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)下列调查中不适合抽样调查的是( )
A.调查陕西省中学生近视情况 B.了解全国食盐加碘情况
C.调查某小麦新品种的发芽率 D.调查某班学生骑自行车上学情况
2.(本题3分)为了了解参加某运动会的200名运动员的年龄情况,从中抽查了20名运动员的年龄,就这个问题来说,下面说法正确的是( )
A.200名运动员是总体 B.每个运动员是总体
C.20名运动员是所抽取的一个样本 D.样本容量是20
3.(本题3分)如图所示的是某中学九(2)班的数学一模成绩统计图(每组含前一个数值,不含后一个数值).关于该统计图,下列说法错误的是( )
A.该班的总人数是40 B.成绩在90分分之间的人数最多
C.优秀(分)的人数是22 D.成绩在80分分的人数占总人数的
4.(本题3分)为调查某校232名学生的体重情况,从中随机抽取40名学生进行测量,这40名学生的体重是( )
A.总体 B.个体 C.样本 D.样本容量
5.(本题3分)某校从800名学生的百米测试成绩中随机抽取了100名学生的百米测试成绩进行了调查,下列说法正确的是( )
A.该调查方式是普查 B.每名学生的百米测试成绩是个体
C.样本是800 名学生 D.100名学生的百米测试成绩是总体
6.(本题3分)小冬爸爸5月份的工资总收入约是元,按照如图进行支配,那么用于教育的费用约是( )
A.元 B.元 C.元 D.元
7.(本题3分)下列结论中正确的是( )
A.检测一批进口食品的质量应采用普查;
B.反映本学年数学成绩的变化情况应采用扇形统计图;
C.从万名考生的成绩中抽取名考生的成绩作为样本,样本容量是万;
D.为了了解我校七年级学生的视力情况,从中抽取名学生进行视力检查.在这次调查中,总体是我校七年级学生视力的全体.
8.(本题3分)下列各项调查中,更适合全面调查的是( )
A.某校七(1)班学生最喜欢的学科 B.端午节最受欢迎粽子的口味
C.某品牌电视机的使用寿命 D.昆明市初中学生的课外活动时间
9.(本题3分)为了更好地掌握国民经济发展水平,尤其是我国的人口发展水平,国务院制定了在2022年进行第八次人口普查方案,为了解全国各省份人口数占全国人口数的百分比,最适合使用的统计图是( )
A.折线统计图 B.扇形统计图
C.条形统计图 D.频数分布直方图
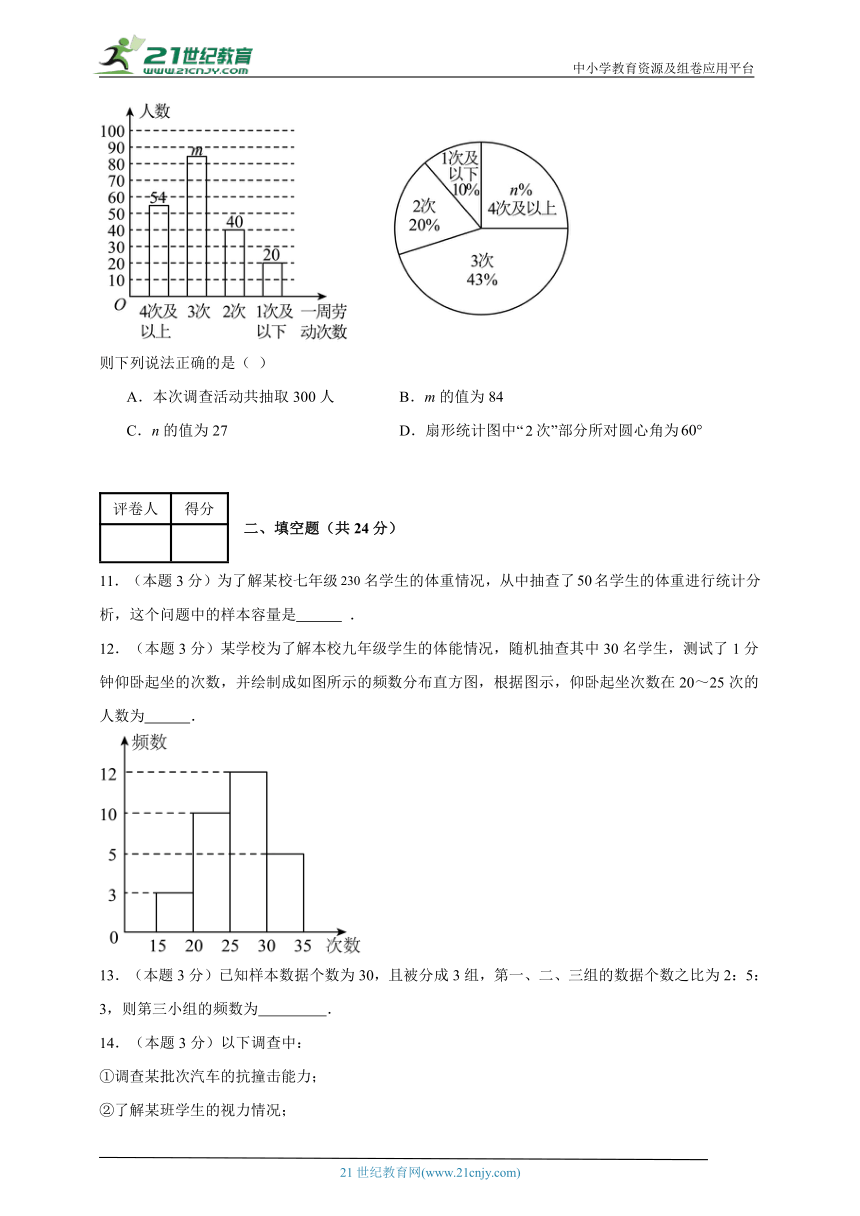
10.(本题3分)2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》,市教育局发布了“普通中小学校劳动教育状况评价指标”,为了了解某校学生一周劳动次数的情况,随机抽取若干学生进行调查,得到如图所示的统计图表:
则下列说法正确的是( )
A.本次调查活动共抽取300人 B.m的值为84
C.n的值为27 D.扇形统计图中“次”部分所对圆心角为
评卷人得分
二、填空题(共24分)
11.(本题3分)为了解某校七年级名学生的体重情况,从中抽查了名学生的体重进行统计分析,这个问题中的样本容量是 .
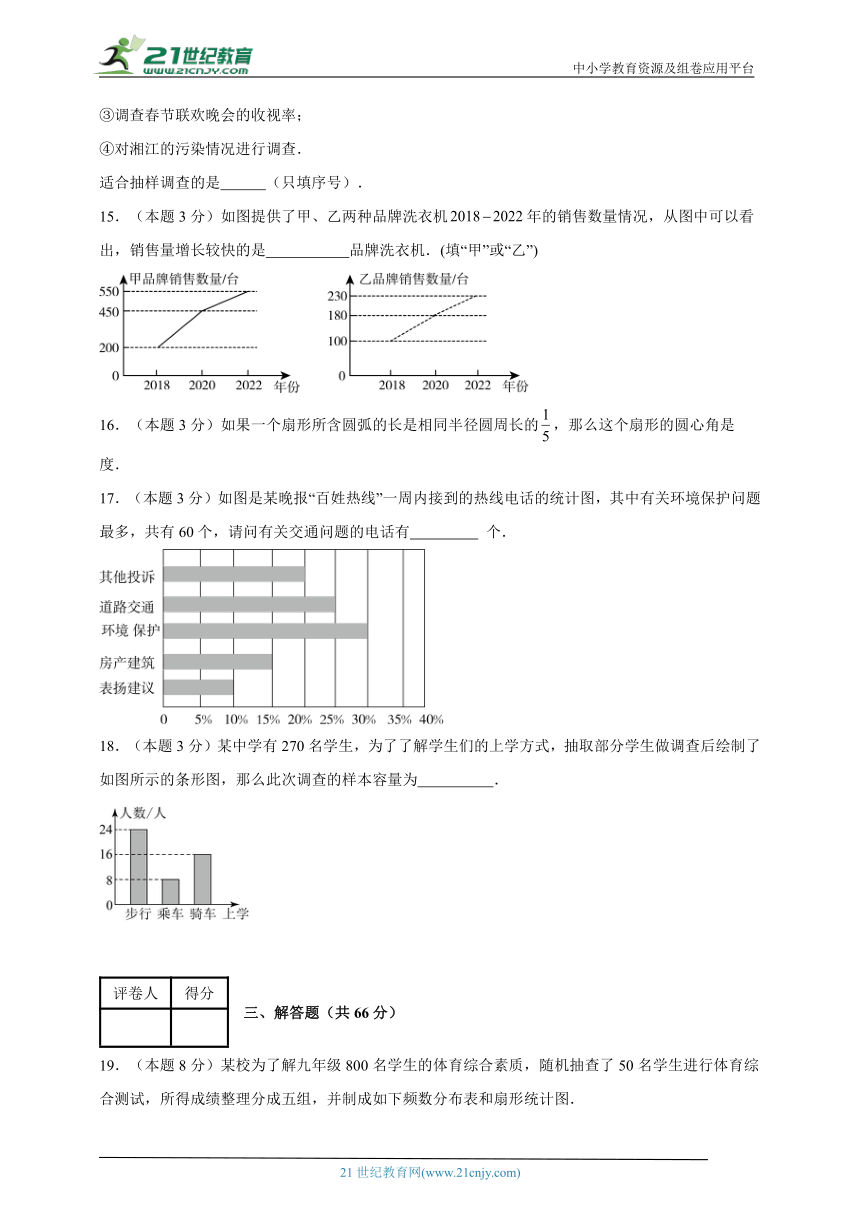
12.(本题3分)某学校为了解本校九年级学生的体能情况,随机抽查其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,根据图示,仰卧起坐次数在20~25次的人数为 .
13.(本题3分)已知样本数据个数为30,且被分成3组,第一、二、三组的数据个数之比为2:5:3,则第三小组的频数为 .
14.(本题3分)以下调查中:
①调查某批次汽车的抗撞击能力;
②了解某班学生的视力情况;
③调查春节联欢晚会的收视率;
④对湘江的污染情况进行调查.
适合抽样调查的是 (只填序号).
15.(本题3分)如图提供了甲、乙两种品牌洗衣机年的销售数量情况,从图中可以看出,销售量增长较快的是 品牌洗衣机.(填“甲”或“乙”)
16.(本题3分)如果一个扇形所含圆弧的长是相同半径圆周长的,那么这个扇形的圆心角是 度.
17.(本题3分)如图是某晚报“百姓热线”一周内接到的热线电话的统计图,其中有关环境保护问题最多,共有60个,请问有关交通问题的电话有 个.
18.(本题3分)某中学有270名学生,为了了解学生们的上学方式,抽取部分学生做调查后绘制了如图所示的条形图,那么此次调查的样本容量为 .
评卷人得分
三、解答题(共66分)
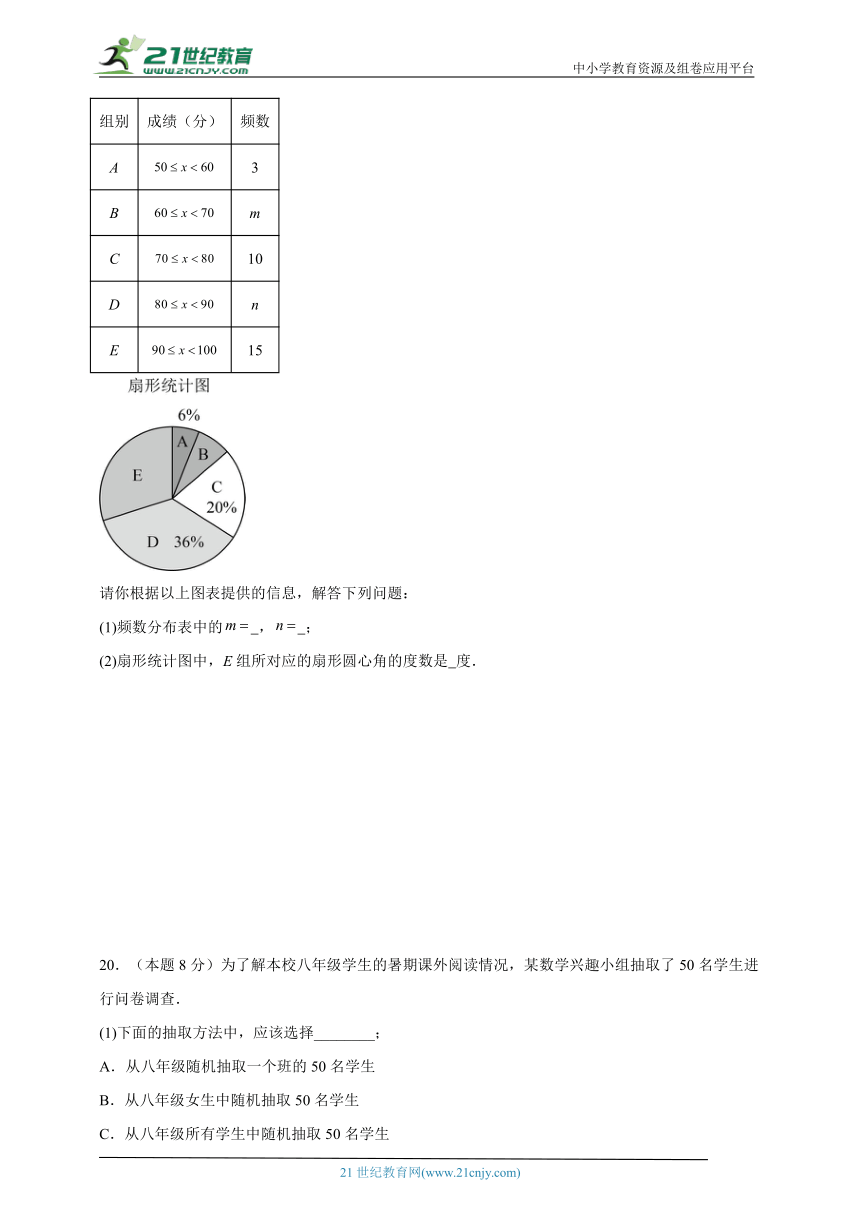
19.(本题8分)某校为了解九年级800名学生的体育综合素质,随机抽查了50名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图.
组别 成绩(分) 频数
A 3
B m
C 10
D n
E 15
请你根据以上图表提供的信息,解答下列问题:
(1)频数分布表中的 , ;
(2)扇形统计图中,E组所对应的扇形圆心角的度数是 度.
20.(本题8分)为了解本校八年级学生的暑期课外阅读情况,某数学兴趣小组抽取了50名学生进行问卷调查.
(1)下面的抽取方法中,应该选择________;
A.从八年级随机抽取一个班的50名学生
B.从八年级女生中随机抽取50名学生
C.从八年级所有学生中随机抽取50名学生
(2)对调查数据进行整理,得到下列两幅尚不完整的统计图表:
暑期课外阅读情况统计表
阅读数量(本) 人数
0 5
1 25
2 a
3本及以上 5
合计 50
统计表中的a=________,补全条形统计图;
(3)根据上述调查情况,写一条你的看法.
21.(本题10分)小聪家准备购买一台电视机,小聪将收集到的某地区A,B,C三种品牌电视机销售情况的有关数据统计如下:
根据上述三个统计图,请解答:
(1)年三种品牌电视机销售总量最多的是______品牌,2021年比2020年A品牌月平均销售量的增长率为______.
(2)年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小聪家购买哪种品牌的电视机?说说你的理由.
22.(本题10分)“2023中国(西安)国际机器人展览会”于2023年3月在西安国际会展中心隆重举行.某校八年级一班老师为了培养学生们的学习兴趣,利用活动课时间向大家详细介绍了“A工业机器人,B人工智能,C无人机,D服务机器人”四种常见类型机器人的相关知识,课后老师为了了解学生对哪种机器人更感兴趣,向全班同学开展调查,并根据统计数据绘制了图1和图2两幅尚不完整的统计图.请你根据图中信息解答下列问题:
(1)八年级一班的学生总人数是 ,并补全条形统计图;
(2)八年级一班的学生最感兴趣的机器人类型是 ;
(3)该校学生总人数为1000人,请估计该校学生中对“B人工智能”和“C无人机”两类机器人更感兴趣的学生共有多少人?
23.(本题10分)某校六年级有学生400人,课后服务设置了不同的兴趣小组,参加各个兴趣小组的情况如图所示
(1)参加体育兴趣小组的有多少人.
(2)参加语文兴趣小组的人数比参加英语兴趣小组的人数多多少人.
(3)数学兴趣小组所在的扇形的圆心角是多少度.
24.(本题10分)国家卫健委公布的数据显示截止到2021年年底,我国60岁及以上的老年人口数量达到了亿,小明为了了解七年级(1)班同学各自家庭中老年人口数量情况,对七年级(1)班全体同学各自家庭中老年人口数量进行了调查,根据调查的结果制作了两幅不完整统计图,请根据统计图中的信息完成下列问题.
(1)求七年级(1)班的学生人数;
(2)请补全条形统计图;
(3)计算扇形统计图中部分所对的圆心角的度数.
25.(本题10分)某中学六年级共有学生171人,其中1班有48人.为了迎接新年,全年级师生组织了一场迎新演出,各班同学踊跃参加,如图是各班参演学生人数情况统计图.请根据图中提供的信息解答下列问题:
(1)表示“2班参演学生人数”的扇形的圆心角度数是______.
(2)如果3班的参演学生人数比4班的少9人,求全年级的参演学生人数.
(3)如果1班和2班的参演学生人数之和是这两个班级学生总人数的,3班和4班的参演学生人数之和是这两个班级学生总人数的,求2班的学生总人数.
参考答案:
1.D
【分析】本题考查抽样调查,涉及调查分类,理解抽样调查及全面调查,根据选项中的描述逐项验证即可得到答案,熟记抽样调查定义是解决问题的关键.
【详解】解:A、调查陕西省中学生近视情况,一个省内的中学生数量较大,应采用抽样调查,不符合题意;
B、了解全国食盐加碘情况,在全国范围内,应采用抽样调查,不符合题意;
C、调查某小麦新品种的发芽率,需要大范围调查,应采用抽样调查,不符合题意;
D、调查某班学生骑自行车上学情况,由于人数较少,适合全面调查,选项符合题意;
故选:D.
2.D
【分析】本题主要考查了总体,样本,样本容量的定义,根据样本、总体、样本容量的定义,进行分析即可.总体:我们把所要考察的对象的全体叫做总体;样本容量:样本容量是样本中包含的个体的数目,不能带单位;样本:从总体中取出的一部分个体叫做这个总体的一个样本.
【详解】解:A、200名运动员的年龄情况是总体,原说法错误,不符合题意;
B、200名运动员的年龄情况是总体,原说法错误,不符合题意;
C、20名运动员的年龄是所抽取的一个样本,原说法错误,不符合题意;
D、样本容量是20,原说法正确,符合题意;
故选;D.
3.C
【分析】本题主要考查了频数分布直方图,从直方图上获得所需信息是解题的关键.
根据从直方图上获取的信息逐项判断即可解答.
【详解】解:A.该班的总人数是,故A选项说法正确,但不符合题意;
B.由统计图可知,成绩在90分分之间的人数是14,是最多的,故B选项说法正确,但不符合题意;
C.优秀(分)的人数是,故C选项说法错误,符合题意;
D.成绩在80分的人数是12,占总人数的,故D选项说法正确,但不符合题意.
故选:C.
4.C
【分析】本题主要考查了样本、总体、个体的定义,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.总体是指考查的对象的全体;个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
【详解】解:这40名学生的体重是总体中的一个样本.40是样本容量,一个学生的体重是个体,232名学生的体重是总体.
故选:C.
5.B
【分析】本题考查抽样调查相关概念,解题的关键是掌握相关的定义,根据相关定义处理即可.
【详解】解:A.此调查方式为抽样调查,本选项不合题意;
B.每名学生的百米测试成绩是个体,根据定义,本选项符合题意;
C.样本是100名学生的测试成绩,本选项不合题意;
D.800名学生的百米测试成绩是总体,本选项不合题意.
故选:B.
6.B
【分析】本题考查根据扇形统计图计算项目费用,利用乘以占比即可得到答案;
【详解】解:由题意可得,
用于教育的费用约是:(元),
故选:B.
7.D
【分析】本题考查抽样调查、统计图的选择、样本容量及总体,解题的关键是依据抽样调查、统计图的选择、样本容量及总体的意义对各选项逐一判断,据此解答即可.
【详解】解:A.检测一批进口食品的质量应采用抽样调查,故此选项不符合题意;
B.反映你本学年数学成绩的变化情况宜采用折线统计图,故此选项不符合题意;
C.从5万名考生的成绩中抽取名考生的成绩作为样本,样本容量是,故此选项不符合题意;
D.我校七年级学生视力的全体是总体,故此选项符合题意.
故选:D.
8.A
【分析】本题考查了全面调查与抽样调查.根据全面调查与抽样调查的特点,逐一判断即可解答.
【详解】A选项:调查某校七(1)班学生最喜欢的学科,调查范围小,更适合全面调查,故本选项符合题意;
B选项:调查端午节最受欢迎粽子的口味,调查对象多,更适合抽样调查,故本选项不符合题意;
C选项:调查某品牌电视机的使用寿命,调查具有破坏性,更适合抽样调查,故本选项不符合题意;
D选项:调查昆明市初中学生的课外活动时间,调查对象多,更适合抽样调查,故本选项不符合题意;
故选:A
9.B
【分析】本题考查统计图的选择及频数(率)分布直方图,条形统计图能清楚地表示出每个项目中的具体数目,易于比较数据之间的差别;用扇形的面积表示部分在总体中所占的百分比,易于显示每组数据相对于总数的大小;折线统计图能清楚地反映事物的变化情况,显示数据变化趋势;直方图在数量表示上比较确切,但不够直观、形象,不利于分析数据分布的总体态势.
【详解】解:为了解全国各省份人口数占全国人口数的百分比,最适合使用的统计图是扇形统计图,
故选:B.
10.C
【分析】根据一周劳动次数次以下的人数和所占的百分比,即可求得本次抽取的人数,用总人数乘以次的人数所占的百分比求出的值,用次及以上的人数除以总人数即可得出的值,用乘以劳动次数为次的人数所占的百分比即可.
【详解】解:A.这次调查活动共抽取(人),故原说法错误,不符合题意;
B.,故原说法错误,不符合题意;
C.,即的值为,说法正确,符合题意;
D.扇形统计图中“次”部分所对圆心角为:,说法错误,不符合题意.
故选:C.
【点睛】本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
11.
【分析】本题考查了总体、个体、样本、样本容量,根据总体、个体、样本、样本容量的意义,即可解答.
【详解】解:为了解某校七年级名学生的体重情况,从中抽查了名学生的体重进行统计分析,这个问题中的样本容量是,
故答案为:50
12.10
【分析】本题考查读频数分布直方图的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
【详解】解:读图可知:仰卧起坐次数在20~25次的人数是10,
故答案为:10.
13.9
【分析】本题考查了频数;根据三组数据个数的比及总个数,即可求得结果.
【详解】解:;
故答案为:9.
14.①③④
【分析】本题考查全面调查与抽样调查,当在要求精确,难度相对不大,实验无破坏性的情况下应选择全面调查;当考查对象很多或考查会造成破坏,以及考查经费和时间都有限时,应选择抽样调查.
【详解】解:①调查某批次的汽车的抗撞击力,危险性较大,而且破坏性较强,故应抽样调查;
②了解某班学生的身高情况,涉及人数较少,适合全面调查;
③调查春节联欢晚会的收视率,涉及人数较多,适合抽样调查;
④对湘江的污染情况进行调查,适合抽样调查.
故答案为:①③④.
15.甲
【分析】本题考查了折线统计图,解题的关键是计算出两种品牌的增长量,而单纯从折线的陡峭情况来判断,很易错选乙品牌.结合折线统计图中的数据,分别求出甲、乙各自的增长量即可求出答案.
【详解】解:从折线统计图中可以看出:
甲品牌2018年的销售量约为200台,2022年约为550台,则从年甲品牌增长了(台);
乙品牌2018年的销售量为100台,2022年的销售量为230台,则从年,乙品牌中销售量增长了(台).
∴甲品牌销售量增长的较快.
故答案为:甲.
16.
【分析】本题考查扇形圆心角问题,利用乘以弧长占比即可得到答案;
【详解】解:∵圆弧的长是相同半径圆周长的,
∴这个扇形的圆心角是:,
故答案为:.
17.50
【分析】本题考查用样本估计总体及条形统计图.根据条形统计图可以看出:环境保护60个占总体的,即可求得热线电话的总的个数,再根据交通问题所占的比例即可求解.
【详解】解:有关道路交通问题的电话有:个,,
故答案为:50.
18.
【分析】本题主要考查了求样本容量,根据样本容量的定义进行求解即可:一个样本包括的个体数量叫做样本容量可得答案.熟知相关定义是解题的关键,样本容量是指样本中包含个体的数目,没有单位.
【详解】解:由题意得,样本容量为,
故答案为:.
19.(1)4,18
(2)108
【分析】本题考查频数分布表和扇形统计图的应用.
(1)根据D组的占比可求得的值,再用50减去其他各个频数即可得出的值;
(2)根据E组的频数,求得其百分数,用这个百分数乘即可得出答案.
【详解】(1)解:,
,
故答案为:4,18;
(2)解:E组所对应的扇形圆心角的度数是,
故答案为:108.
20.(1)C
(2)见解析,15
(3)见解析
【详解】(1)C
(2)补全条形统计图如图所示. 15
(3)大多数学生暑期课外阅读数量不够多,要加强宣传课外阅读的重要性(答案不唯一).
21.(1)B,
(2)2021年其他品牌的电视机年销售总量是万台
(3)见解析
【分析】(1)从条形统计图、折线统计图可以得出答案;
(2)求出总销售量及“其它”的所占的百分比,即可得出答案;
(3)从市场占有率、平均销售量、增长率等方面提出建议.
【详解】(1)解:由条形统计图可得,年三种品牌电视机销售总量最多的是B品牌;
由折线统计图可得,2021年比2020年A品牌月平均销售量的增长率为:;
故答案为:B,;
(2)解:(万台),
,
(万台),
答:2020年2021年其他品牌的电视机年销售总量是万台;
(3)解:因为B品牌2021年的市场占有率最高,且5年的月销售量最稳定;建议购买B品牌,
因为A品牌近五年的月平均销售总量逐年稳步上升,建议购买A品牌,答案不唯一
【点睛】考查条形统计图、折线统计图、扇形统计图的意义,理解统计图中各个数量及数量之间的关系是解决问题的关键.
22.(1)50,见解析
(2)B人工智能
(3)680人
【分析】(1)根据扇形统计图与条形统计图中D的数据即可得到样本容量;用样本容量分别减去A、C、D的人数可得B的人数,进而补全条形统计图;
(2)观察统计图可得答案;
(3)用1000乘样本中对“B人工智能” 和“C无人机”两类机器人更感兴趣的学生所占比例可得答案.
【详解】(1)解:八年级一班的学生总人数是:;
其中对“B人工智能“感兴趣的学生人数为:5,
补全条形统计图如下:
故答案为:50;
(2)解:观察统计图可得八年级一班的学生最感兴趣的机器人类型是B人工智能.
故答案为:B人工智能;
(3)解:(人),
答:估计该校学生中对“B人工智能“和“C无人机”两类机器人更感兴趣的学生大约共有680人.
【点睛】本题考查条形统计图与扇形统计图,用样本估计总体,解题的关键是找到部分及占比来求出总数.
23.(1)120人
(2)60人
(3)
【分析】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
(1)把六年级学生总人数看作单位“1”,根据减法的意义,用减法算出体育的百分比,再与400相乘,即可解答;
(1)把六年级学生总人数看作单位“1”,根据已知一个数的百分之几是多少,求语文兴趣小组的人数和参加英语兴趣小组的人数,再运用减法,即可作答;
(3)数学兴趣小组的百分比乘上,用乘法解答.
【详解】(1)解:
则(人)
∴参加体育兴趣小组的有人;
(2)解:语文兴趣小组的人数:(人);
参加英语兴趣小组的人数:(人);
则(人);
∴参加语文兴趣小组的人数比参加英语兴趣小组的人数多人;
(3)解:
∴数学兴趣小组所在的扇形的圆心角是度.
24.(1)50人
(2)见解析
(3)
【分析】本题考查了条形统计图与扇形统计图信息关联;
(1)根据组的人数除以占比,即可求解;
(2)用总人数减去其他组别的人数的的人数,进而画出统计图;
(3)用乘以组的占比,即可求解.
【详解】(1)解:(人)
答:所以七年级(1)班的人数为50人
(2)
如图所示:
(3)解:
答:部分所对的圆心角度数是
25.(1)
(2)全年级的参演学生人数为72人
(3)2班的学生总人数为42人
【分析】本题考查扇形统计图,一元一次方程的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
(1)根据扇形统计图中的数据,可以计算出“2班参演学生人数”的扇形的圆心角度数;
(2)根据3班的参演学生人数比4班的少9人,列式计算即可;
(3)根据题意列式计算即可.
【详解】(1)解: ,
答:表示“2班参演学生人数”的扇形的圆心角度数是,
(2)解:(人,
答:全年级的参演学生人数为72人;
(3)解:设2班的学生总人数为人,
根据题意得,,
解得,
答:2班的学生总人数为42人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学八年级数据的收集与整理
单元测试 (冀教版) 基础卷二含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)下列调查中不适合抽样调查的是( )
A.调查陕西省中学生近视情况 B.了解全国食盐加碘情况
C.调查某小麦新品种的发芽率 D.调查某班学生骑自行车上学情况
2.(本题3分)为了了解参加某运动会的200名运动员的年龄情况,从中抽查了20名运动员的年龄,就这个问题来说,下面说法正确的是( )
A.200名运动员是总体 B.每个运动员是总体
C.20名运动员是所抽取的一个样本 D.样本容量是20
3.(本题3分)如图所示的是某中学九(2)班的数学一模成绩统计图(每组含前一个数值,不含后一个数值).关于该统计图,下列说法错误的是( )
A.该班的总人数是40 B.成绩在90分分之间的人数最多
C.优秀(分)的人数是22 D.成绩在80分分的人数占总人数的
4.(本题3分)为调查某校232名学生的体重情况,从中随机抽取40名学生进行测量,这40名学生的体重是( )
A.总体 B.个体 C.样本 D.样本容量
5.(本题3分)某校从800名学生的百米测试成绩中随机抽取了100名学生的百米测试成绩进行了调查,下列说法正确的是( )
A.该调查方式是普查 B.每名学生的百米测试成绩是个体
C.样本是800 名学生 D.100名学生的百米测试成绩是总体
6.(本题3分)小冬爸爸5月份的工资总收入约是元,按照如图进行支配,那么用于教育的费用约是( )
A.元 B.元 C.元 D.元
7.(本题3分)下列结论中正确的是( )
A.检测一批进口食品的质量应采用普查;
B.反映本学年数学成绩的变化情况应采用扇形统计图;
C.从万名考生的成绩中抽取名考生的成绩作为样本,样本容量是万;
D.为了了解我校七年级学生的视力情况,从中抽取名学生进行视力检查.在这次调查中,总体是我校七年级学生视力的全体.
8.(本题3分)下列各项调查中,更适合全面调查的是( )
A.某校七(1)班学生最喜欢的学科 B.端午节最受欢迎粽子的口味
C.某品牌电视机的使用寿命 D.昆明市初中学生的课外活动时间
9.(本题3分)为了更好地掌握国民经济发展水平,尤其是我国的人口发展水平,国务院制定了在2022年进行第八次人口普查方案,为了解全国各省份人口数占全国人口数的百分比,最适合使用的统计图是( )
A.折线统计图 B.扇形统计图
C.条形统计图 D.频数分布直方图
10.(本题3分)2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》,市教育局发布了“普通中小学校劳动教育状况评价指标”,为了了解某校学生一周劳动次数的情况,随机抽取若干学生进行调查,得到如图所示的统计图表:
则下列说法正确的是( )
A.本次调查活动共抽取300人 B.m的值为84
C.n的值为27 D.扇形统计图中“次”部分所对圆心角为
评卷人得分
二、填空题(共24分)
11.(本题3分)为了解某校七年级名学生的体重情况,从中抽查了名学生的体重进行统计分析,这个问题中的样本容量是 .
12.(本题3分)某学校为了解本校九年级学生的体能情况,随机抽查其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,根据图示,仰卧起坐次数在20~25次的人数为 .
13.(本题3分)已知样本数据个数为30,且被分成3组,第一、二、三组的数据个数之比为2:5:3,则第三小组的频数为 .
14.(本题3分)以下调查中:
①调查某批次汽车的抗撞击能力;
②了解某班学生的视力情况;
③调查春节联欢晚会的收视率;
④对湘江的污染情况进行调查.
适合抽样调查的是 (只填序号).
15.(本题3分)如图提供了甲、乙两种品牌洗衣机年的销售数量情况,从图中可以看出,销售量增长较快的是 品牌洗衣机.(填“甲”或“乙”)
16.(本题3分)如果一个扇形所含圆弧的长是相同半径圆周长的,那么这个扇形的圆心角是 度.
17.(本题3分)如图是某晚报“百姓热线”一周内接到的热线电话的统计图,其中有关环境保护问题最多,共有60个,请问有关交通问题的电话有 个.
18.(本题3分)某中学有270名学生,为了了解学生们的上学方式,抽取部分学生做调查后绘制了如图所示的条形图,那么此次调查的样本容量为 .
评卷人得分
三、解答题(共66分)
19.(本题8分)某校为了解九年级800名学生的体育综合素质,随机抽查了50名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图.
组别 成绩(分) 频数
A 3
B m
C 10
D n
E 15
请你根据以上图表提供的信息,解答下列问题:
(1)频数分布表中的 , ;
(2)扇形统计图中,E组所对应的扇形圆心角的度数是 度.
20.(本题8分)为了解本校八年级学生的暑期课外阅读情况,某数学兴趣小组抽取了50名学生进行问卷调查.
(1)下面的抽取方法中,应该选择________;
A.从八年级随机抽取一个班的50名学生
B.从八年级女生中随机抽取50名学生
C.从八年级所有学生中随机抽取50名学生
(2)对调查数据进行整理,得到下列两幅尚不完整的统计图表:
暑期课外阅读情况统计表
阅读数量(本) 人数
0 5
1 25
2 a
3本及以上 5
合计 50
统计表中的a=________,补全条形统计图;
(3)根据上述调查情况,写一条你的看法.
21.(本题10分)小聪家准备购买一台电视机,小聪将收集到的某地区A,B,C三种品牌电视机销售情况的有关数据统计如下:
根据上述三个统计图,请解答:
(1)年三种品牌电视机销售总量最多的是______品牌,2021年比2020年A品牌月平均销售量的增长率为______.
(2)年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小聪家购买哪种品牌的电视机?说说你的理由.
22.(本题10分)“2023中国(西安)国际机器人展览会”于2023年3月在西安国际会展中心隆重举行.某校八年级一班老师为了培养学生们的学习兴趣,利用活动课时间向大家详细介绍了“A工业机器人,B人工智能,C无人机,D服务机器人”四种常见类型机器人的相关知识,课后老师为了了解学生对哪种机器人更感兴趣,向全班同学开展调查,并根据统计数据绘制了图1和图2两幅尚不完整的统计图.请你根据图中信息解答下列问题:
(1)八年级一班的学生总人数是 ,并补全条形统计图;
(2)八年级一班的学生最感兴趣的机器人类型是 ;
(3)该校学生总人数为1000人,请估计该校学生中对“B人工智能”和“C无人机”两类机器人更感兴趣的学生共有多少人?
23.(本题10分)某校六年级有学生400人,课后服务设置了不同的兴趣小组,参加各个兴趣小组的情况如图所示
(1)参加体育兴趣小组的有多少人.
(2)参加语文兴趣小组的人数比参加英语兴趣小组的人数多多少人.
(3)数学兴趣小组所在的扇形的圆心角是多少度.
24.(本题10分)国家卫健委公布的数据显示截止到2021年年底,我国60岁及以上的老年人口数量达到了亿,小明为了了解七年级(1)班同学各自家庭中老年人口数量情况,对七年级(1)班全体同学各自家庭中老年人口数量进行了调查,根据调查的结果制作了两幅不完整统计图,请根据统计图中的信息完成下列问题.
(1)求七年级(1)班的学生人数;
(2)请补全条形统计图;
(3)计算扇形统计图中部分所对的圆心角的度数.
25.(本题10分)某中学六年级共有学生171人,其中1班有48人.为了迎接新年,全年级师生组织了一场迎新演出,各班同学踊跃参加,如图是各班参演学生人数情况统计图.请根据图中提供的信息解答下列问题:
(1)表示“2班参演学生人数”的扇形的圆心角度数是______.
(2)如果3班的参演学生人数比4班的少9人,求全年级的参演学生人数.
(3)如果1班和2班的参演学生人数之和是这两个班级学生总人数的,3班和4班的参演学生人数之和是这两个班级学生总人数的,求2班的学生总人数.
参考答案:
1.D
【分析】本题考查抽样调查,涉及调查分类,理解抽样调查及全面调查,根据选项中的描述逐项验证即可得到答案,熟记抽样调查定义是解决问题的关键.
【详解】解:A、调查陕西省中学生近视情况,一个省内的中学生数量较大,应采用抽样调查,不符合题意;
B、了解全国食盐加碘情况,在全国范围内,应采用抽样调查,不符合题意;
C、调查某小麦新品种的发芽率,需要大范围调查,应采用抽样调查,不符合题意;
D、调查某班学生骑自行车上学情况,由于人数较少,适合全面调查,选项符合题意;
故选:D.
2.D
【分析】本题主要考查了总体,样本,样本容量的定义,根据样本、总体、样本容量的定义,进行分析即可.总体:我们把所要考察的对象的全体叫做总体;样本容量:样本容量是样本中包含的个体的数目,不能带单位;样本:从总体中取出的一部分个体叫做这个总体的一个样本.
【详解】解:A、200名运动员的年龄情况是总体,原说法错误,不符合题意;
B、200名运动员的年龄情况是总体,原说法错误,不符合题意;
C、20名运动员的年龄是所抽取的一个样本,原说法错误,不符合题意;
D、样本容量是20,原说法正确,符合题意;
故选;D.
3.C
【分析】本题主要考查了频数分布直方图,从直方图上获得所需信息是解题的关键.
根据从直方图上获取的信息逐项判断即可解答.
【详解】解:A.该班的总人数是,故A选项说法正确,但不符合题意;
B.由统计图可知,成绩在90分分之间的人数是14,是最多的,故B选项说法正确,但不符合题意;
C.优秀(分)的人数是,故C选项说法错误,符合题意;
D.成绩在80分的人数是12,占总人数的,故D选项说法正确,但不符合题意.
故选:C.
4.C
【分析】本题主要考查了样本、总体、个体的定义,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.总体是指考查的对象的全体;个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
【详解】解:这40名学生的体重是总体中的一个样本.40是样本容量,一个学生的体重是个体,232名学生的体重是总体.
故选:C.
5.B
【分析】本题考查抽样调查相关概念,解题的关键是掌握相关的定义,根据相关定义处理即可.
【详解】解:A.此调查方式为抽样调查,本选项不合题意;
B.每名学生的百米测试成绩是个体,根据定义,本选项符合题意;
C.样本是100名学生的测试成绩,本选项不合题意;
D.800名学生的百米测试成绩是总体,本选项不合题意.
故选:B.
6.B
【分析】本题考查根据扇形统计图计算项目费用,利用乘以占比即可得到答案;
【详解】解:由题意可得,
用于教育的费用约是:(元),
故选:B.
7.D
【分析】本题考查抽样调查、统计图的选择、样本容量及总体,解题的关键是依据抽样调查、统计图的选择、样本容量及总体的意义对各选项逐一判断,据此解答即可.
【详解】解:A.检测一批进口食品的质量应采用抽样调查,故此选项不符合题意;
B.反映你本学年数学成绩的变化情况宜采用折线统计图,故此选项不符合题意;
C.从5万名考生的成绩中抽取名考生的成绩作为样本,样本容量是,故此选项不符合题意;
D.我校七年级学生视力的全体是总体,故此选项符合题意.
故选:D.
8.A
【分析】本题考查了全面调查与抽样调查.根据全面调查与抽样调查的特点,逐一判断即可解答.
【详解】A选项:调查某校七(1)班学生最喜欢的学科,调查范围小,更适合全面调查,故本选项符合题意;
B选项:调查端午节最受欢迎粽子的口味,调查对象多,更适合抽样调查,故本选项不符合题意;
C选项:调查某品牌电视机的使用寿命,调查具有破坏性,更适合抽样调查,故本选项不符合题意;
D选项:调查昆明市初中学生的课外活动时间,调查对象多,更适合抽样调查,故本选项不符合题意;
故选:A
9.B
【分析】本题考查统计图的选择及频数(率)分布直方图,条形统计图能清楚地表示出每个项目中的具体数目,易于比较数据之间的差别;用扇形的面积表示部分在总体中所占的百分比,易于显示每组数据相对于总数的大小;折线统计图能清楚地反映事物的变化情况,显示数据变化趋势;直方图在数量表示上比较确切,但不够直观、形象,不利于分析数据分布的总体态势.
【详解】解:为了解全国各省份人口数占全国人口数的百分比,最适合使用的统计图是扇形统计图,
故选:B.
10.C
【分析】根据一周劳动次数次以下的人数和所占的百分比,即可求得本次抽取的人数,用总人数乘以次的人数所占的百分比求出的值,用次及以上的人数除以总人数即可得出的值,用乘以劳动次数为次的人数所占的百分比即可.
【详解】解:A.这次调查活动共抽取(人),故原说法错误,不符合题意;
B.,故原说法错误,不符合题意;
C.,即的值为,说法正确,符合题意;
D.扇形统计图中“次”部分所对圆心角为:,说法错误,不符合题意.
故选:C.
【点睛】本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
11.
【分析】本题考查了总体、个体、样本、样本容量,根据总体、个体、样本、样本容量的意义,即可解答.
【详解】解:为了解某校七年级名学生的体重情况,从中抽查了名学生的体重进行统计分析,这个问题中的样本容量是,
故答案为:50
12.10
【分析】本题考查读频数分布直方图的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
【详解】解:读图可知:仰卧起坐次数在20~25次的人数是10,
故答案为:10.
13.9
【分析】本题考查了频数;根据三组数据个数的比及总个数,即可求得结果.
【详解】解:;
故答案为:9.
14.①③④
【分析】本题考查全面调查与抽样调查,当在要求精确,难度相对不大,实验无破坏性的情况下应选择全面调查;当考查对象很多或考查会造成破坏,以及考查经费和时间都有限时,应选择抽样调查.
【详解】解:①调查某批次的汽车的抗撞击力,危险性较大,而且破坏性较强,故应抽样调查;
②了解某班学生的身高情况,涉及人数较少,适合全面调查;
③调查春节联欢晚会的收视率,涉及人数较多,适合抽样调查;
④对湘江的污染情况进行调查,适合抽样调查.
故答案为:①③④.
15.甲
【分析】本题考查了折线统计图,解题的关键是计算出两种品牌的增长量,而单纯从折线的陡峭情况来判断,很易错选乙品牌.结合折线统计图中的数据,分别求出甲、乙各自的增长量即可求出答案.
【详解】解:从折线统计图中可以看出:
甲品牌2018年的销售量约为200台,2022年约为550台,则从年甲品牌增长了(台);
乙品牌2018年的销售量为100台,2022年的销售量为230台,则从年,乙品牌中销售量增长了(台).
∴甲品牌销售量增长的较快.
故答案为:甲.
16.
【分析】本题考查扇形圆心角问题,利用乘以弧长占比即可得到答案;
【详解】解:∵圆弧的长是相同半径圆周长的,
∴这个扇形的圆心角是:,
故答案为:.
17.50
【分析】本题考查用样本估计总体及条形统计图.根据条形统计图可以看出:环境保护60个占总体的,即可求得热线电话的总的个数,再根据交通问题所占的比例即可求解.
【详解】解:有关道路交通问题的电话有:个,,
故答案为:50.
18.
【分析】本题主要考查了求样本容量,根据样本容量的定义进行求解即可:一个样本包括的个体数量叫做样本容量可得答案.熟知相关定义是解题的关键,样本容量是指样本中包含个体的数目,没有单位.
【详解】解:由题意得,样本容量为,
故答案为:.
19.(1)4,18
(2)108
【分析】本题考查频数分布表和扇形统计图的应用.
(1)根据D组的占比可求得的值,再用50减去其他各个频数即可得出的值;
(2)根据E组的频数,求得其百分数,用这个百分数乘即可得出答案.
【详解】(1)解:,
,
故答案为:4,18;
(2)解:E组所对应的扇形圆心角的度数是,
故答案为:108.
20.(1)C
(2)见解析,15
(3)见解析
【详解】(1)C
(2)补全条形统计图如图所示. 15
(3)大多数学生暑期课外阅读数量不够多,要加强宣传课外阅读的重要性(答案不唯一).
21.(1)B,
(2)2021年其他品牌的电视机年销售总量是万台
(3)见解析
【分析】(1)从条形统计图、折线统计图可以得出答案;
(2)求出总销售量及“其它”的所占的百分比,即可得出答案;
(3)从市场占有率、平均销售量、增长率等方面提出建议.
【详解】(1)解:由条形统计图可得,年三种品牌电视机销售总量最多的是B品牌;
由折线统计图可得,2021年比2020年A品牌月平均销售量的增长率为:;
故答案为:B,;
(2)解:(万台),
,
(万台),
答:2020年2021年其他品牌的电视机年销售总量是万台;
(3)解:因为B品牌2021年的市场占有率最高,且5年的月销售量最稳定;建议购买B品牌,
因为A品牌近五年的月平均销售总量逐年稳步上升,建议购买A品牌,答案不唯一
【点睛】考查条形统计图、折线统计图、扇形统计图的意义,理解统计图中各个数量及数量之间的关系是解决问题的关键.
22.(1)50,见解析
(2)B人工智能
(3)680人
【分析】(1)根据扇形统计图与条形统计图中D的数据即可得到样本容量;用样本容量分别减去A、C、D的人数可得B的人数,进而补全条形统计图;
(2)观察统计图可得答案;
(3)用1000乘样本中对“B人工智能” 和“C无人机”两类机器人更感兴趣的学生所占比例可得答案.
【详解】(1)解:八年级一班的学生总人数是:;
其中对“B人工智能“感兴趣的学生人数为:5,
补全条形统计图如下:
故答案为:50;
(2)解:观察统计图可得八年级一班的学生最感兴趣的机器人类型是B人工智能.
故答案为:B人工智能;
(3)解:(人),
答:估计该校学生中对“B人工智能“和“C无人机”两类机器人更感兴趣的学生大约共有680人.
【点睛】本题考查条形统计图与扇形统计图,用样本估计总体,解题的关键是找到部分及占比来求出总数.
23.(1)120人
(2)60人
(3)
【分析】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
(1)把六年级学生总人数看作单位“1”,根据减法的意义,用减法算出体育的百分比,再与400相乘,即可解答;
(1)把六年级学生总人数看作单位“1”,根据已知一个数的百分之几是多少,求语文兴趣小组的人数和参加英语兴趣小组的人数,再运用减法,即可作答;
(3)数学兴趣小组的百分比乘上,用乘法解答.
【详解】(1)解:
则(人)
∴参加体育兴趣小组的有人;
(2)解:语文兴趣小组的人数:(人);
参加英语兴趣小组的人数:(人);
则(人);
∴参加语文兴趣小组的人数比参加英语兴趣小组的人数多人;
(3)解:
∴数学兴趣小组所在的扇形的圆心角是度.
24.(1)50人
(2)见解析
(3)
【分析】本题考查了条形统计图与扇形统计图信息关联;
(1)根据组的人数除以占比,即可求解;
(2)用总人数减去其他组别的人数的的人数,进而画出统计图;
(3)用乘以组的占比,即可求解.
【详解】(1)解:(人)
答:所以七年级(1)班的人数为50人
(2)
如图所示:
(3)解:
答:部分所对的圆心角度数是
25.(1)
(2)全年级的参演学生人数为72人
(3)2班的学生总人数为42人
【分析】本题考查扇形统计图,一元一次方程的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
(1)根据扇形统计图中的数据,可以计算出“2班参演学生人数”的扇形的圆心角度数;
(2)根据3班的参演学生人数比4班的少9人,列式计算即可;
(3)根据题意列式计算即可.
【详解】(1)解: ,
答:表示“2班参演学生人数”的扇形的圆心角度数是,
(2)解:(人,
答:全年级的参演学生人数为72人;
(3)解:设2班的学生总人数为人,
根据题意得,,
解得,
答:2班的学生总人数为42人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
