2.6.2 扇形面积 课件(共22张PPT)2023-2024学年湘教版九年级数学下册
文档属性
| 名称 | 2.6.2 扇形面积 课件(共22张PPT)2023-2024学年湘教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 840.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 17:21:29 | ||
图片预览






文档简介
(共22张PPT)
第二章 圆
2.6.2 扇形面积
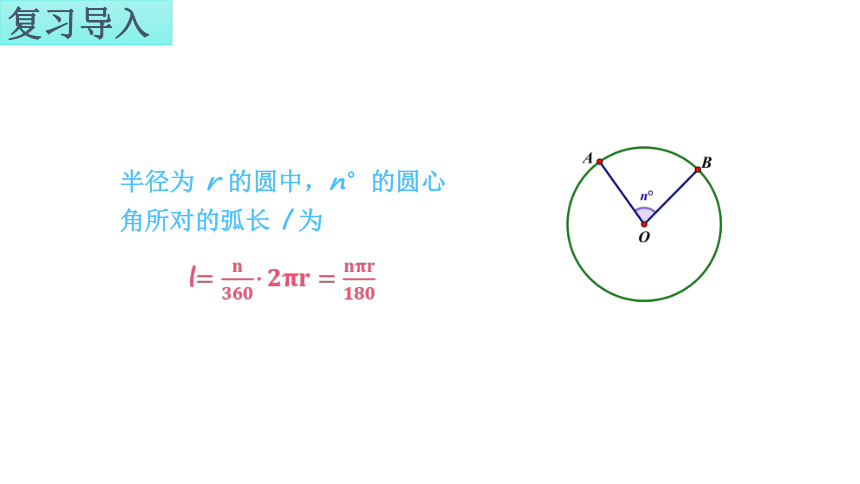
复习导入
半径为 r 的圆中,n°的圆心角所对的弧长 l 为
l
探究新知
如图所示是一把圆弧形状的扇子的示意图,你能求出做这把扇子用了多少纸吗?
探究新知
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
蓝色部分是一个扇形, 记作扇形 OAB.
我们可以发现,扇形面积与组成扇形的圆心角的大小有关,在同一个圆中,圆心角越大, 扇形面积也越大.
探究新知
如何求半径为 r,圆心角为 n°的扇形的面积呢?
圆的面积可看作是_______的圆心角所在的扇形面积.
设圆的半径为 r, 1°的圆心角所在的扇形面积为______.
n°的圆心角所在的扇形面积为______.
360°
因为圆绕圆心旋转任意角度,都能与自身重合,所以圆心角为1°的扇形能够相互重合,从而圆心角为1°的扇形的面积等于圆面积的 。
知识要点
半径为 r 的圆中,圆心角为 n°的扇形的面积为
又因为扇形的弧长为 ,因此
在两个公式中,存在l、R、n、S四个量,我们只要知道其中两个就可以求得其他的两个 .
lr
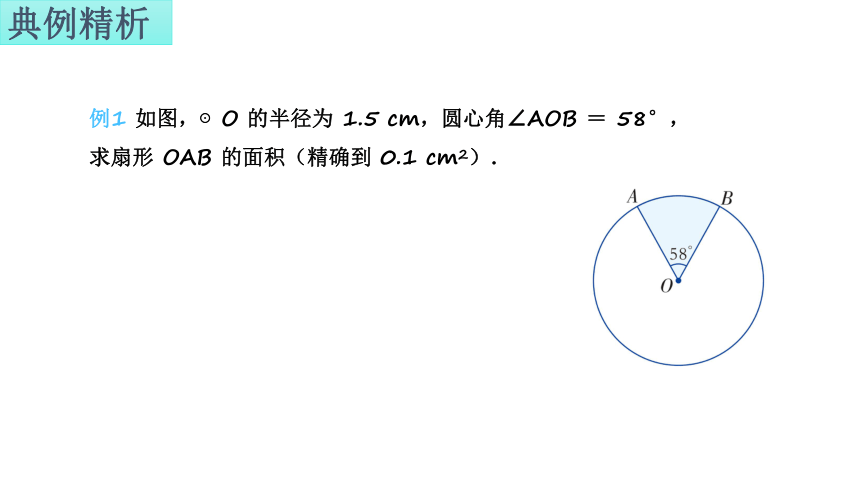
典例精析
例1 如图,⊙O 的半径为 1.5 cm,圆心角∠AOB = 58°,求扇形 OAB 的面积(精确到 0.1 cm2).
典例精析
例1 如图,⊙O 的半径为 1.5 cm,圆心角∠AOB = 58°,求扇形 OAB 的面积(精确到 0.1 cm2).
解 ∵ r = 1.5 cm ,n = 58 ,
cm2)
典例精析
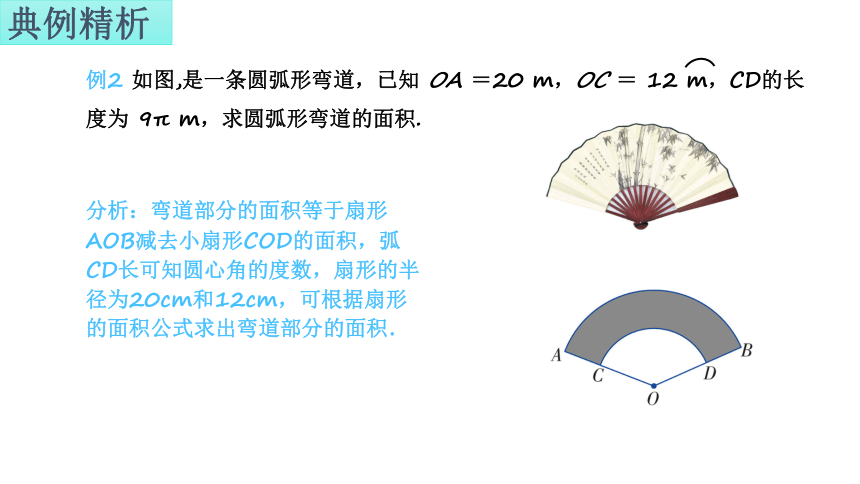
例2 如图,是一条圆弧形弯道,已知 OA =20 m,OC = 12 m,CD的长度为 9π m,求圆弧形弯道的面积.
分析:弯道部分的面积等于扇形AOB减去小扇形COD的面积,弧CD长可知圆心角的度数,扇形的半径为20cm和12cm,可根据扇形的面积公式求出弯道部分的面积.
典例精析
例2 如图,是一条圆弧形弯道,已知 OA =20 m,OC = 12 m,CD的长度为 9π m,求圆弧形弯道的面积.
解:设∠AOB = n°,
∵ OC = 12 m,CD的长度为 9π m,
∴
解得 n = 135,即圆心角∠COD = 135 ° .
∴m2)
m2)
∴S扇形ACDB = S扇形OAB - S扇形OCD = 150π - 54π = 96π(m2)
答:这条圆弧形弯道的面积为 96π m2.
典例精析
例3 如图,正方形ABCD 内接于半径为2的⊙O ,则图中阴影部分的面积为 。
分析:根据对称性可知阴影部分的面积等于圆的四分之一减去正方形的四分之一,求出圆的内接正方形的边长,即可解.
知识要点
求阴影部分面积的问题常用方法:
(1)公式法:所求面积的图形是一个规则图形,如三角形、特殊四边形、扇形等,这时可直接利用相关面积计算公式进行求解;如例1.
(2)和差法:
①S总体-S空白=S阴影
②所求面积的图形是一个不规则图形,可将其通过转化变成多个规则图形面积的和或差,进行求解;如例2.
(3)移动法:直接求面积较复杂或无法计算时,将图形位置进行移动(平移、旋转、对称、割补)使其成为规则图形或者为使用和差法提供条件,从而求解。包括割补法、平移法、旋转法、等积代换法。如例3.
1.弓形是一个什么样的图形?
弓形:由弦及其所对的弧组成的图形叫做弓形.
2.如何由扇形的面积公式推导弓形的面积公式?
(1)当弓形的弧小于半圆时,弓形的面积等于扇形面积与三角形面积的差;
知识要点
S弓形=S扇形OAB-S AOB
2.如何由扇形的面积公式推导弓形的面积公式?
(2)当弓形的弧大于半圆时,弓形的面积等于扇形面积与三角形面积的和;
(3)当弓形的弧是半圆时,弓形面积是圆面积的一半.
S弓形=S扇形OAB-S AOB
S弓形=S圆
知识要点
当堂练习
1.如图,在⊙O 中,∠AOB = 120°,弦 AB 的长为cm, 求扇形 OAB 的面积.
当堂练习
1.如图,在⊙O 中,∠AOB = 120°,弦 AB 的长为cm, 求扇形 OAB 的面积.
解:作 OD ⊥ AB , 由题可求出OA = 2(cm)
答:扇形 OAB 的面积为 4.2 cm2.
cm2)
当堂练习
2. 如图,分别以△ABC 的顶点 A,B,C 为圆心,以 1 为半径画圆,求图中绿色部分的面积.
当堂练习
2. 如图,分别以△ABC 的顶点 A,B,C 为圆心,以 1 为半径画圆,求图中绿色部分的面积.
解:∠A+ ∠B+ ∠C = 180°
绿色部分可以看成半径为 1,圆心角为180°的扇形.
当堂练习
3. 如图,有一直径是 20 cm 的圆形纸片,现从中剪出一个圆心角是 90°的扇形 ABC,求被剪掉部分的面积.
当堂练习
3. 如图,有一直径是 20 cm 的圆形纸片,现从中剪出一个圆心角是 90°的扇形 ABC,求被剪掉部分的面积.
解:连接BC,则 BC = 20 cm
又因为 AB = AC, 所以△ABC为等腰直角三角形.
求剩余部分的面积?
扩展提升
课堂小结
半径为 r 的圆中,圆心角为 n°的扇形的面积为
又因为扇形的弧长为 ,因此
在两个公式中,存在l、R、n、S四个量,我们只要知道其中两个就可以求得其他的两个 .
lr
第二章 圆
2.6.2 扇形面积
复习导入
半径为 r 的圆中,n°的圆心角所对的弧长 l 为
l
探究新知
如图所示是一把圆弧形状的扇子的示意图,你能求出做这把扇子用了多少纸吗?
探究新知
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
蓝色部分是一个扇形, 记作扇形 OAB.
我们可以发现,扇形面积与组成扇形的圆心角的大小有关,在同一个圆中,圆心角越大, 扇形面积也越大.
探究新知
如何求半径为 r,圆心角为 n°的扇形的面积呢?
圆的面积可看作是_______的圆心角所在的扇形面积.
设圆的半径为 r, 1°的圆心角所在的扇形面积为______.
n°的圆心角所在的扇形面积为______.
360°
因为圆绕圆心旋转任意角度,都能与自身重合,所以圆心角为1°的扇形能够相互重合,从而圆心角为1°的扇形的面积等于圆面积的 。
知识要点
半径为 r 的圆中,圆心角为 n°的扇形的面积为
又因为扇形的弧长为 ,因此
在两个公式中,存在l、R、n、S四个量,我们只要知道其中两个就可以求得其他的两个 .
lr
典例精析
例1 如图,⊙O 的半径为 1.5 cm,圆心角∠AOB = 58°,求扇形 OAB 的面积(精确到 0.1 cm2).
典例精析
例1 如图,⊙O 的半径为 1.5 cm,圆心角∠AOB = 58°,求扇形 OAB 的面积(精确到 0.1 cm2).
解 ∵ r = 1.5 cm ,n = 58 ,
cm2)
典例精析
例2 如图,是一条圆弧形弯道,已知 OA =20 m,OC = 12 m,CD的长度为 9π m,求圆弧形弯道的面积.
分析:弯道部分的面积等于扇形AOB减去小扇形COD的面积,弧CD长可知圆心角的度数,扇形的半径为20cm和12cm,可根据扇形的面积公式求出弯道部分的面积.
典例精析
例2 如图,是一条圆弧形弯道,已知 OA =20 m,OC = 12 m,CD的长度为 9π m,求圆弧形弯道的面积.
解:设∠AOB = n°,
∵ OC = 12 m,CD的长度为 9π m,
∴
解得 n = 135,即圆心角∠COD = 135 ° .
∴m2)
m2)
∴S扇形ACDB = S扇形OAB - S扇形OCD = 150π - 54π = 96π(m2)
答:这条圆弧形弯道的面积为 96π m2.
典例精析
例3 如图,正方形ABCD 内接于半径为2的⊙O ,则图中阴影部分的面积为 。
分析:根据对称性可知阴影部分的面积等于圆的四分之一减去正方形的四分之一,求出圆的内接正方形的边长,即可解.
知识要点
求阴影部分面积的问题常用方法:
(1)公式法:所求面积的图形是一个规则图形,如三角形、特殊四边形、扇形等,这时可直接利用相关面积计算公式进行求解;如例1.
(2)和差法:
①S总体-S空白=S阴影
②所求面积的图形是一个不规则图形,可将其通过转化变成多个规则图形面积的和或差,进行求解;如例2.
(3)移动法:直接求面积较复杂或无法计算时,将图形位置进行移动(平移、旋转、对称、割补)使其成为规则图形或者为使用和差法提供条件,从而求解。包括割补法、平移法、旋转法、等积代换法。如例3.
1.弓形是一个什么样的图形?
弓形:由弦及其所对的弧组成的图形叫做弓形.
2.如何由扇形的面积公式推导弓形的面积公式?
(1)当弓形的弧小于半圆时,弓形的面积等于扇形面积与三角形面积的差;
知识要点
S弓形=S扇形OAB-S AOB
2.如何由扇形的面积公式推导弓形的面积公式?
(2)当弓形的弧大于半圆时,弓形的面积等于扇形面积与三角形面积的和;
(3)当弓形的弧是半圆时,弓形面积是圆面积的一半.
S弓形=S扇形OAB-S AOB
S弓形=S圆
知识要点
当堂练习
1.如图,在⊙O 中,∠AOB = 120°,弦 AB 的长为cm, 求扇形 OAB 的面积.
当堂练习
1.如图,在⊙O 中,∠AOB = 120°,弦 AB 的长为cm, 求扇形 OAB 的面积.
解:作 OD ⊥ AB , 由题可求出OA = 2(cm)
答:扇形 OAB 的面积为 4.2 cm2.
cm2)
当堂练习
2. 如图,分别以△ABC 的顶点 A,B,C 为圆心,以 1 为半径画圆,求图中绿色部分的面积.
当堂练习
2. 如图,分别以△ABC 的顶点 A,B,C 为圆心,以 1 为半径画圆,求图中绿色部分的面积.
解:∠A+ ∠B+ ∠C = 180°
绿色部分可以看成半径为 1,圆心角为180°的扇形.
当堂练习
3. 如图,有一直径是 20 cm 的圆形纸片,现从中剪出一个圆心角是 90°的扇形 ABC,求被剪掉部分的面积.
当堂练习
3. 如图,有一直径是 20 cm 的圆形纸片,现从中剪出一个圆心角是 90°的扇形 ABC,求被剪掉部分的面积.
解:连接BC,则 BC = 20 cm
又因为 AB = AC, 所以△ABC为等腰直角三角形.
求剩余部分的面积?
扩展提升
课堂小结
半径为 r 的圆中,圆心角为 n°的扇形的面积为
又因为扇形的弧长为 ,因此
在两个公式中,存在l、R、n、S四个量,我们只要知道其中两个就可以求得其他的两个 .
lr
