鲁教版七年级数学上册第1章1.5利用三角形全等测距离同步训练题(含答案)
文档属性
| 名称 | 鲁教版七年级数学上册第1章1.5利用三角形全等测距离同步训练题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 147.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-28 00:00:00 | ||
图片预览


文档简介
鲁教版七年级数学上册第1章1.5利用三角形全等测距离同步训练题(含答案)
一.选择题(共6小题)
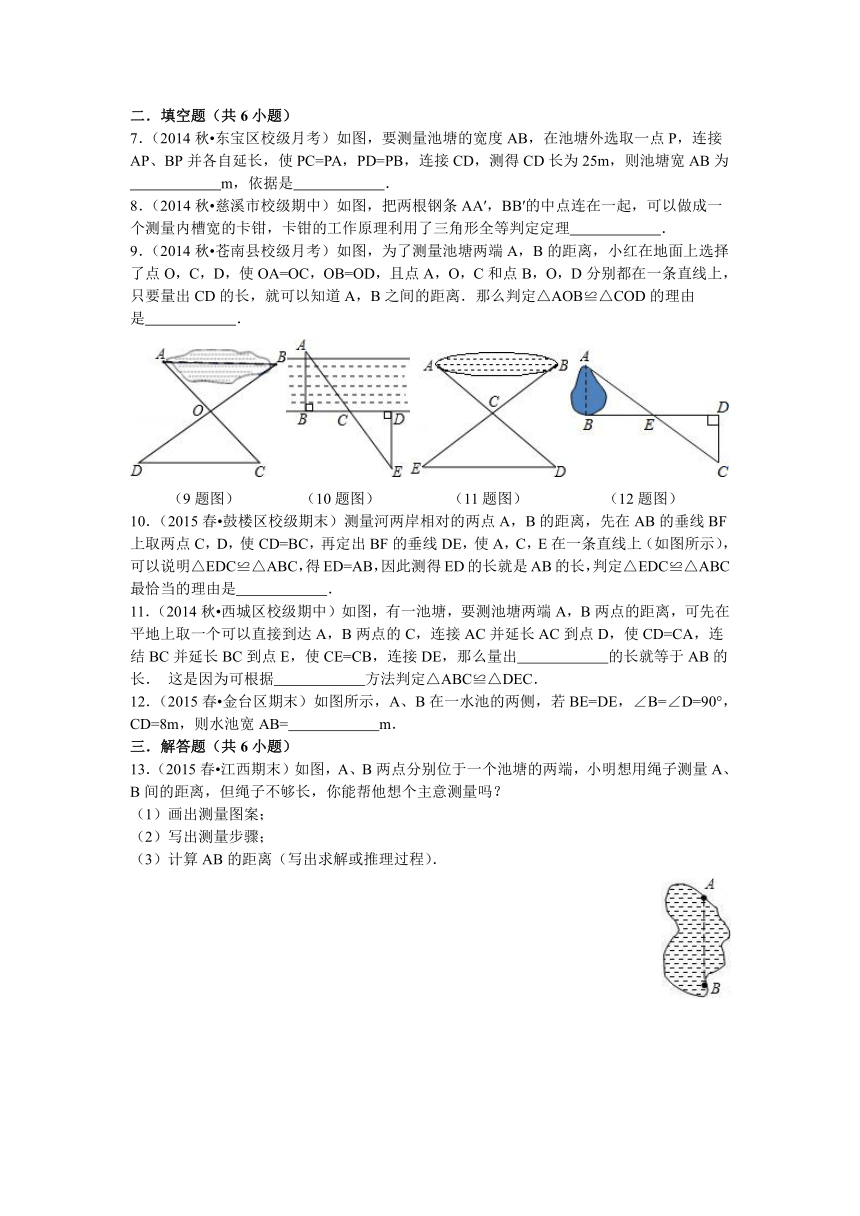
1.(2015春 西城区期中)如图,小明同学把两根等长的木条AC、BD的中点连在一起,做成一个测量某物品内槽宽的工具,此时CD的长等于内槽的宽AB,这种测量方法用到三角形全等的判定方法是( )
A.SAS B. ASA C. SSS D. HL
(1题图) (2题图) (3题图) (4题图) (5题图)
2.(2015 临沂模拟)如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成了一个测量工件,由三角形全等得出A′B′的长等于内槽宽AB;那么判定△OAB≌△OA′B′的理由是( )
A.边角边 B. 角边角 C. 边边边 D. 角角边
3.(2015春 衡南县校级期中)八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,再测出DE的距离,最后根据△ABC≌△DEC得到DE的长即为AB的长.该同学判定△ABC≌△DEC的依据是( )
A.SAS B. AAS C. SSS D. HL
4.(2015春 通川区校级月考)如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.SSS B. SAS C. ASA D. AAS
5.(2014秋 潘集区校级期中)如图,有一池塘,要测量池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长至E,使CE=AC,连结BC并延长至D,使CD=BC,连结DE,根据△ABC≌△EDC可知,量出DE的长,就是A、B的距离,这里△ABC≌△EDC的依据是( )
A.SAS B. ASA C. AAS D. SSS
6.(2015春 沈丘县校级期中)要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在同一条直线上(如图),可以证明在△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长,在这里判定在△ABC≌△EDC的条件是( )
A.ASA B. SAS C. SSS D. HL
(6题图) (7题图) (8题图)
二.填空题(共6小题)
7.(2014秋 东宝区校级月考)如图,要测量池塘的宽度AB,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘宽AB为
m,依据是 .
8.(2014秋 慈溪市校级期中)如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量内槽宽的卡钳,卡钳的工作原理利用了三角形全等判定定理 .
9.(2014秋 苍南县校级月考)如图,为了测量池塘两端A,B的距离,小红在地面上选择了点O,C,D,使OA=OC,OB=OD,且点A,O,C和点B,O,D分别都在一条直线上,只要量出CD的长,就可以知道A,B之间的距离.那么判定△AOB≌△COD的理由是 .
(9题图) (10题图) (11题图) (12题图)
10.(2015春 鼓楼区校级期末)测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是 .
11.(2014秋 西城区校级期中)如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出 的长就等于AB的长. 这是因为可根据 方法判定△ABC≌△DEC.
12.(2015春 金台区期末)如图所示,A、B在一水池的两侧,若BE=DE,∠B=∠D=90°,CD=8m,则水池宽AB= m.
三.解答题(共6小题)
13.(2015春 江西期末)如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,你能帮他想个主意测量吗?
(1)画出测量图案;
(2)写出测量步骤;
(3)计算AB的距离(写出求解或推理过程).
14.(2015春 章丘市校级期中)如图A、B两点分别位于一座小山脚的两端,小明想要测量A、B两点间的距离,请你帮他设计一个测量方案,测出AB的距离.并说明其中的道理.
15.(2015 周口模拟)如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得的DE的长就是AB的长,为什么?
16.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AB的平行线MF,连接MD并延长,在延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你知道其中的道理吗?
17.如图所示,要测水池中一荷花E距岸边A和岸边D的距离.作法如下:
(1)任作线段AB,取其中点O;
(2)连接DO并延长使DO=CO;
(3)连接BC;
(4)用仪器测得E,O在一条直线上,并交CB于点F.要测AE,DE,测量BF,CF即可,为什么?
18.有一座小山,现要在小山A、B的两端开一条隧道,施工队要知道A、B两端的距离,于是先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,你能说说其中的道理吗?
鲁教版七年级数学上册第1章1.5利用三角形全等测距离同步训练题参考答案
一.选择题(共6小题)
1.A 2.A 3.A 4.C 5.A 6.A
二.填空题(共6小题)
7.25 SAS 8.SAS 9.SAS 10.ASA 11.DE SAS 12.8
三.解答题(共6小题)
13.解:(1)如图;
(2)①首先先在地上取一个可以直接到A、B的点C,找到AC、BC的中点D、E,连接DE.然后量出DE的长.
②根据DE的长以及中位线计算出AB的长.
(3)根据DE的长结合三角形的中位线定理可知:AB=2DE.
(13题图) (14题图)
14.解:如图所示:在AB下方找一点O,连接BO,并延长使BO=B′O,连接AO,并延长使AO=A′O,
在△AOB和△A′OB′中∵,∴△AOB≌△A′OB′(SAS),
∴AB=A′B′,
量出A′B′的长即可.
15.解:∵AB⊥BF,DE⊥BF,∴∠ABC=∠EDC=90°,
又∵直线BF与AE交于点C,∴∠ACB=∠ECD(对顶角相等),
∵CD=BC,
∴△ABC≌△EDC,
∴AB=ED,
即测得DE的长就是A,B两点间的距离.
16.解:∵在△BDE和△FDM中,∴△BDE≌△FDM(SAS),
∴∠BEM=∠FME,
∴BE∥MF,
∵AB∥MF,
∴A、C、E三点在一条直线上.
17.解:∵O是AB的中点,
∴AO=BO,
在△AOD和△BOC中,,∴△AOD≌△BOC(SAS),∴∠A=∠B,
∵E,O在一条直线上,
∴∠AOE=∠BOF,
在△AOE和△BOF中,,∴△AOE≌△BOF(ASA),
∴AE=BF,
同理可证DE=CF.
18.解:在△ABC和△CED中,
AC=CD,∠ACB=∠ECD(对顶角),EC=BC,
∴△ABC≌△DEC,
∴AB=ED,
即量出DE的长,就是A、B的距离
一.选择题(共6小题)
1.(2015春 西城区期中)如图,小明同学把两根等长的木条AC、BD的中点连在一起,做成一个测量某物品内槽宽的工具,此时CD的长等于内槽的宽AB,这种测量方法用到三角形全等的判定方法是( )
A.SAS B. ASA C. SSS D. HL
(1题图) (2题图) (3题图) (4题图) (5题图)
2.(2015 临沂模拟)如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成了一个测量工件,由三角形全等得出A′B′的长等于内槽宽AB;那么判定△OAB≌△OA′B′的理由是( )
A.边角边 B. 角边角 C. 边边边 D. 角角边
3.(2015春 衡南县校级期中)八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,再测出DE的距离,最后根据△ABC≌△DEC得到DE的长即为AB的长.该同学判定△ABC≌△DEC的依据是( )
A.SAS B. AAS C. SSS D. HL
4.(2015春 通川区校级月考)如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.SSS B. SAS C. ASA D. AAS
5.(2014秋 潘集区校级期中)如图,有一池塘,要测量池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长至E,使CE=AC,连结BC并延长至D,使CD=BC,连结DE,根据△ABC≌△EDC可知,量出DE的长,就是A、B的距离,这里△ABC≌△EDC的依据是( )
A.SAS B. ASA C. AAS D. SSS
6.(2015春 沈丘县校级期中)要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在同一条直线上(如图),可以证明在△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长,在这里判定在△ABC≌△EDC的条件是( )
A.ASA B. SAS C. SSS D. HL
(6题图) (7题图) (8题图)
二.填空题(共6小题)
7.(2014秋 东宝区校级月考)如图,要测量池塘的宽度AB,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘宽AB为
m,依据是 .
8.(2014秋 慈溪市校级期中)如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量内槽宽的卡钳,卡钳的工作原理利用了三角形全等判定定理 .
9.(2014秋 苍南县校级月考)如图,为了测量池塘两端A,B的距离,小红在地面上选择了点O,C,D,使OA=OC,OB=OD,且点A,O,C和点B,O,D分别都在一条直线上,只要量出CD的长,就可以知道A,B之间的距离.那么判定△AOB≌△COD的理由是 .
(9题图) (10题图) (11题图) (12题图)
10.(2015春 鼓楼区校级期末)测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是 .
11.(2014秋 西城区校级期中)如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出 的长就等于AB的长. 这是因为可根据 方法判定△ABC≌△DEC.
12.(2015春 金台区期末)如图所示,A、B在一水池的两侧,若BE=DE,∠B=∠D=90°,CD=8m,则水池宽AB= m.
三.解答题(共6小题)
13.(2015春 江西期末)如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,你能帮他想个主意测量吗?
(1)画出测量图案;
(2)写出测量步骤;
(3)计算AB的距离(写出求解或推理过程).
14.(2015春 章丘市校级期中)如图A、B两点分别位于一座小山脚的两端,小明想要测量A、B两点间的距离,请你帮他设计一个测量方案,测出AB的距离.并说明其中的道理.
15.(2015 周口模拟)如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得的DE的长就是AB的长,为什么?
16.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AB的平行线MF,连接MD并延长,在延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你知道其中的道理吗?
17.如图所示,要测水池中一荷花E距岸边A和岸边D的距离.作法如下:
(1)任作线段AB,取其中点O;
(2)连接DO并延长使DO=CO;
(3)连接BC;
(4)用仪器测得E,O在一条直线上,并交CB于点F.要测AE,DE,测量BF,CF即可,为什么?
18.有一座小山,现要在小山A、B的两端开一条隧道,施工队要知道A、B两端的距离,于是先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,你能说说其中的道理吗?
鲁教版七年级数学上册第1章1.5利用三角形全等测距离同步训练题参考答案
一.选择题(共6小题)
1.A 2.A 3.A 4.C 5.A 6.A
二.填空题(共6小题)
7.25 SAS 8.SAS 9.SAS 10.ASA 11.DE SAS 12.8
三.解答题(共6小题)
13.解:(1)如图;
(2)①首先先在地上取一个可以直接到A、B的点C,找到AC、BC的中点D、E,连接DE.然后量出DE的长.
②根据DE的长以及中位线计算出AB的长.
(3)根据DE的长结合三角形的中位线定理可知:AB=2DE.
(13题图) (14题图)
14.解:如图所示:在AB下方找一点O,连接BO,并延长使BO=B′O,连接AO,并延长使AO=A′O,
在△AOB和△A′OB′中∵,∴△AOB≌△A′OB′(SAS),
∴AB=A′B′,
量出A′B′的长即可.
15.解:∵AB⊥BF,DE⊥BF,∴∠ABC=∠EDC=90°,
又∵直线BF与AE交于点C,∴∠ACB=∠ECD(对顶角相等),
∵CD=BC,
∴△ABC≌△EDC,
∴AB=ED,
即测得DE的长就是A,B两点间的距离.
16.解:∵在△BDE和△FDM中,∴△BDE≌△FDM(SAS),
∴∠BEM=∠FME,
∴BE∥MF,
∵AB∥MF,
∴A、C、E三点在一条直线上.
17.解:∵O是AB的中点,
∴AO=BO,
在△AOD和△BOC中,,∴△AOD≌△BOC(SAS),∴∠A=∠B,
∵E,O在一条直线上,
∴∠AOE=∠BOF,
在△AOE和△BOF中,,∴△AOE≌△BOF(ASA),
∴AE=BF,
同理可证DE=CF.
18.解:在△ABC和△CED中,
AC=CD,∠ACB=∠ECD(对顶角),EC=BC,
∴△ABC≌△DEC,
∴AB=ED,
即量出DE的长,就是A、B的距离
