2023-2024学年数学九年级下册苏科版第6章图形的相似易错精选题(含答案)
文档属性
| 名称 | 2023-2024学年数学九年级下册苏科版第6章图形的相似易错精选题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 578.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 21:13:12 | ||
图片预览


文档简介
2023-2024学年数学九年级下册苏科版第6章图形的相似易错精选题
一、选择题
1.若,则的值为( )
A.1 B. C. D.
2.如图,在中,,,若,则等于( )
A.6 B.8 C.7 D.5
3.如图,直线l1∥l2∥l3,如果AB=3,BC=5,EF=4,则DE的长是( )
A. B. C. D.
4.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,则扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
5.如图,△ABC∽△ACD,相似比为2,已知AD的长为2,则AB的长为( )
A.8 B. C.6 D.4
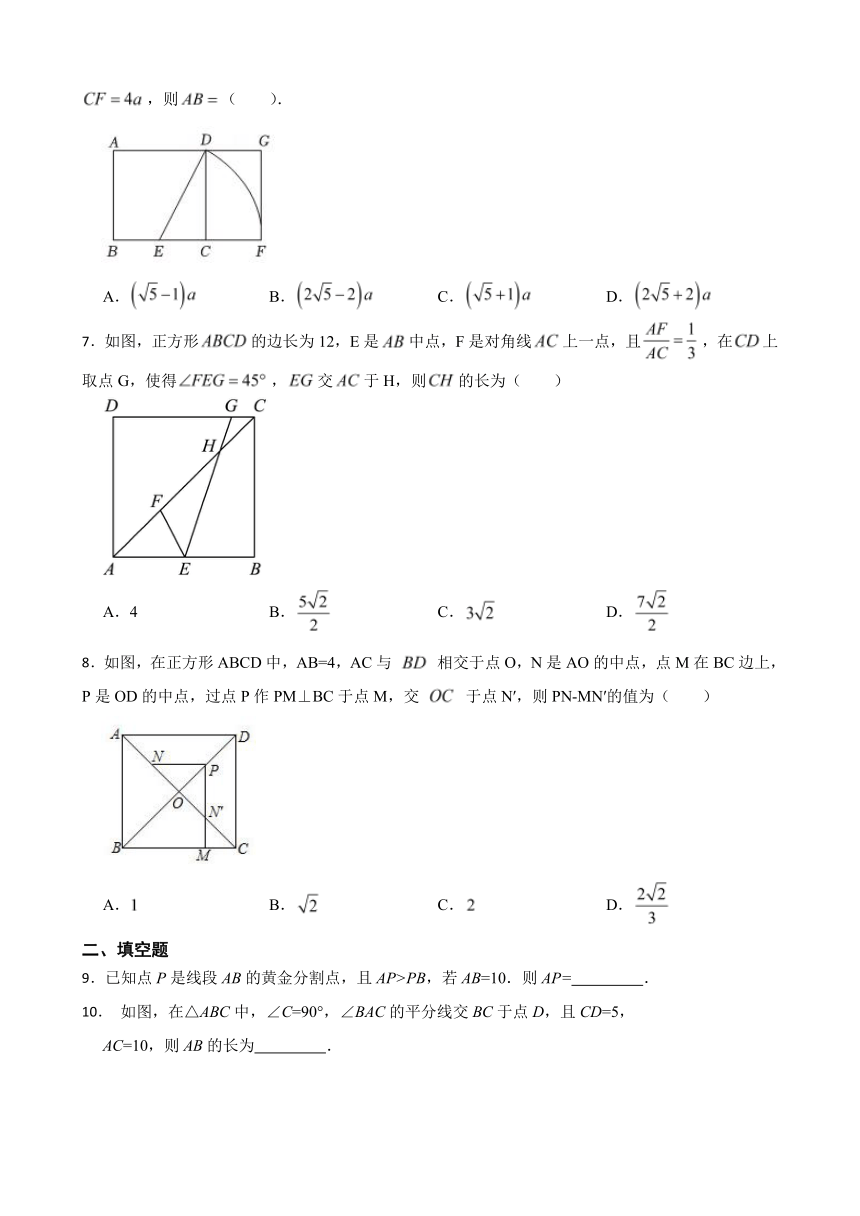
6.黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形的底边取中点E,以E为圆心,线段为半径作圆,其与底边的延长线交于点F,这样就把正方形延伸为矩形,称其为黄金矩形.若,则( ).
A. B. C. D.
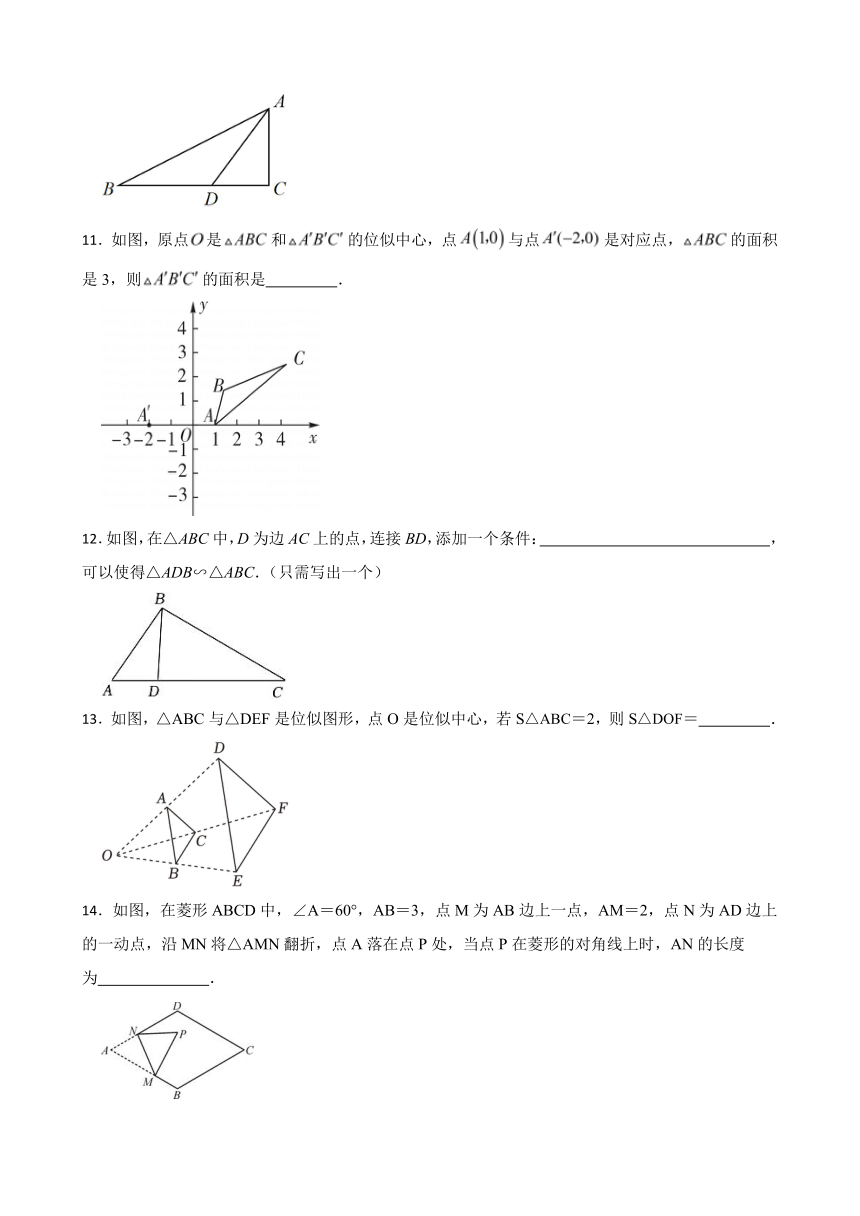
7.如图,正方形的边长为12,E是中点,F是对角线上一点,且,在上取点G,使得,交于H,则的长为( )
A.4 B. C. D.
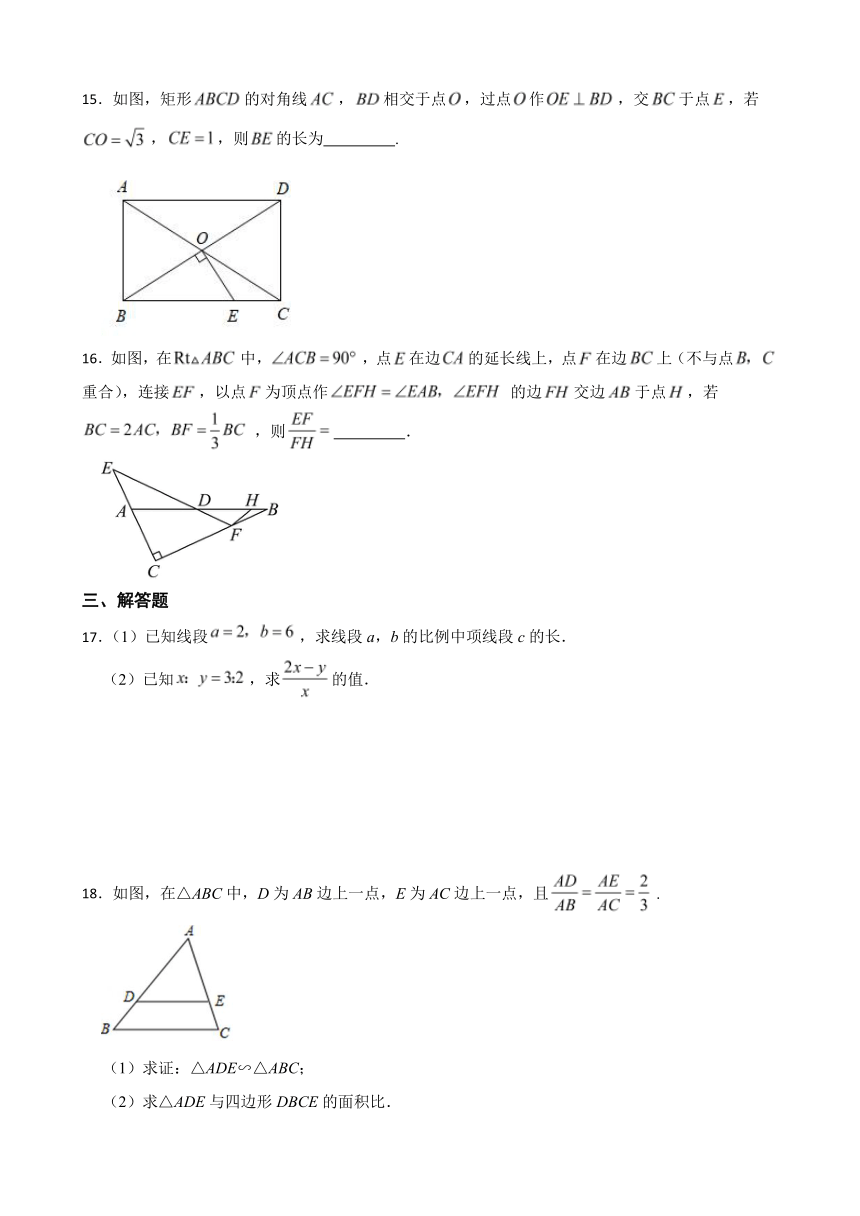
8.如图,在正方形ABCD中,AB=4,AC与 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交 于点N′,则PN-MN′的值为( )
A. B. C. D.
二、填空题
9.已知点P是线段AB的黄金分割点,且AP>PB,若AB=10.则AP= .
10. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,且CD=5,
AC=10,则AB的长为 .
11.如图,原点是和的位似中心,点与点是对应点,的面积是3,则的面积是 .
12.如图,在△ABC中,D为边AC上的点,连接BD,添加一个条件: ,可以使得△ADB∽△ABC.(只需写出一个)
13.如图,△ABC与△DEF是位似图形,点O是位似中心,若S△ABC=2,则S△DOF= .
14.如图,在菱形ABCD中,∠A=60°,AB=3,点M为AB边上一点,AM=2,点N为AD边上的一动点,沿MN将△AMN翻折,点A落在点P处,当点P在菱形的对角线上时,AN的长度为 .
15.如图,矩形的对角线,相交于点,过点作,交于点,若,,则的长为 .
16.如图,在中,,点在边的延长线上,点在边上(不与点重合),连接,以点为顶点作的边交边于点,若,则 .
三、解答题
17.(1)已知线段,求线段a,b的比例中项线段c的长.
(2)已知,求的值.
18.如图,在△ABC中,D为AB边上一点,E为AC边上一点,且.
(1)求证:△ADE∽△ABC;
(2)求△ADE与四边形DBCE的面积比.
19.如图,在平行四边形ABCD中,F为CD边上一点,连接BF并延长至点E,连接DE,CE,AF.已知,.
(1)求证:;
(2)连接BD,BD与AF相交于点O,连OE.
①若,求证:四边形OBCE为菱形;
②若,,请求出此时BD的长.
20.已知:如图,四边形ABCD中,为对角线BD的中点,点在边AD上,CF交BD于点.
(1)求证:四边形AECF为菱形;
(2),求证:.
21.如图,AB是⊙O的直径,AB=2,⊙O的弦CD⊥AB于点E,CD=6.过点C作⊙O的切线交AB的延长线于点F,连结BC.
(1)求证:CB平分
(2)G为AD上一点,连结CG交AB于点H,若CH =3GH,求BH的长.
22.如图1,滹沱河是山西地区一条途经了舟山和太行山的知名河流,这条河流的流域面积达到了2.73万平方公里,其发源地处于山西省繁峙县泰戏山桥儿沟村,这条河流早在《山海经》中就有出现过,被叫做为虔池.为了估算河流的宽度,我们在河的对岸选定一个目标P,在近岸取点A和C,使点P、A、C共线且与河垂直,接着在过点C且与直线PC垂直的直线上选择适当的点D,确定PD与过点A且与PC垂直的直线交点B,测得AC=50m,CD=120m,AB=80m,请根据这些数据求河的宽度PA.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】C
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】
10.【答案】
11.【答案】12
12.【答案】∠ABD=∠C(答案不唯一)
13.【答案】8
14.【答案】2或5-
15.【答案】2
16.【答案】
17.【答案】(1)解:∵线段,线段c是线段a、b的比例中项,
∴,
∴(负值舍去);
(2)解:∵,
∴可设,
∴.
18.【答案】(1)略
(2)解:4:5
19.【答案】(1)证明:∵四边形ABCD是平行四边形,∴,,,
∵,∴,,∵,
∴,∵,∴;
(2)解:①∵,∴,∴,
∴,∴,∴,∴,
∵,∴四边形AOED是平行四边形,∴且,
∵四边形ABCD是平行四边形,∴且,
∴且,∴四边形BCEO是平行四边形,
∵,∴四边形OBCE为菱形.
②∵,∴,∵,∴,
∵且,∴,
∵,,∴,
∴,∴,
整理得:,∴(舍去)或,
∴,∵,∴.
20.【答案】(1)证明:∵∠BAD=90°,E为BD的中点,
∴AE=DE=BD,
∵CF=BD,
∴AE=CF=DE,
∵CF∥AE,∴四边形AECF是平行四边形,
∵∠BCD=90°,E为BD的中点,∴CE=BD,
∴AE=CE,
∴四边形AECF为菱形;
(2)∵四边形AECF为菱形,
∴AD∥CE,
∴∠ADE=∠DEC,
∵∠DCG=∠DEC,∴∠ADE=∠DCG,
∵AE∥CF,∴∠EAD=∠CFD,∴△ADE∽△FCD,
∴∴CF DE=AD CD,
∵AE=CF=DE,∴AE2=AD DC.
21.【答案】(1)解:如图,连接OC,
,
,
,
,
是⊙O的切线,
,
,
平分
(2)解:如图,连接OG,作,
,
,
,,
,,
,
,
,
,
,
,
,
,
,
,
设,,
,
,
.
22.【答案】解:由题意得,AB⊥PC,CD⊥PC,AC=50m,CD=120m,AB=80m,
∴AB∥CD,
∴∠PAB=∠PCD,∠PBA=∠PDC,
∴△PAB∽△PCD,
∴,即,
∴,
解得PA=100,
答:PA的长为100m.
一、选择题
1.若,则的值为( )
A.1 B. C. D.
2.如图,在中,,,若,则等于( )
A.6 B.8 C.7 D.5
3.如图,直线l1∥l2∥l3,如果AB=3,BC=5,EF=4,则DE的长是( )
A. B. C. D.
4.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,则扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
5.如图,△ABC∽△ACD,相似比为2,已知AD的长为2,则AB的长为( )
A.8 B. C.6 D.4
6.黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形的底边取中点E,以E为圆心,线段为半径作圆,其与底边的延长线交于点F,这样就把正方形延伸为矩形,称其为黄金矩形.若,则( ).
A. B. C. D.
7.如图,正方形的边长为12,E是中点,F是对角线上一点,且,在上取点G,使得,交于H,则的长为( )
A.4 B. C. D.
8.如图,在正方形ABCD中,AB=4,AC与 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交 于点N′,则PN-MN′的值为( )
A. B. C. D.
二、填空题
9.已知点P是线段AB的黄金分割点,且AP>PB,若AB=10.则AP= .
10. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,且CD=5,
AC=10,则AB的长为 .
11.如图,原点是和的位似中心,点与点是对应点,的面积是3,则的面积是 .
12.如图,在△ABC中,D为边AC上的点,连接BD,添加一个条件: ,可以使得△ADB∽△ABC.(只需写出一个)
13.如图,△ABC与△DEF是位似图形,点O是位似中心,若S△ABC=2,则S△DOF= .
14.如图,在菱形ABCD中,∠A=60°,AB=3,点M为AB边上一点,AM=2,点N为AD边上的一动点,沿MN将△AMN翻折,点A落在点P处,当点P在菱形的对角线上时,AN的长度为 .
15.如图,矩形的对角线,相交于点,过点作,交于点,若,,则的长为 .
16.如图,在中,,点在边的延长线上,点在边上(不与点重合),连接,以点为顶点作的边交边于点,若,则 .
三、解答题
17.(1)已知线段,求线段a,b的比例中项线段c的长.
(2)已知,求的值.
18.如图,在△ABC中,D为AB边上一点,E为AC边上一点,且.
(1)求证:△ADE∽△ABC;
(2)求△ADE与四边形DBCE的面积比.
19.如图,在平行四边形ABCD中,F为CD边上一点,连接BF并延长至点E,连接DE,CE,AF.已知,.
(1)求证:;
(2)连接BD,BD与AF相交于点O,连OE.
①若,求证:四边形OBCE为菱形;
②若,,请求出此时BD的长.
20.已知:如图,四边形ABCD中,为对角线BD的中点,点在边AD上,CF交BD于点.
(1)求证:四边形AECF为菱形;
(2),求证:.
21.如图,AB是⊙O的直径,AB=2,⊙O的弦CD⊥AB于点E,CD=6.过点C作⊙O的切线交AB的延长线于点F,连结BC.
(1)求证:CB平分
(2)G为AD上一点,连结CG交AB于点H,若CH =3GH,求BH的长.
22.如图1,滹沱河是山西地区一条途经了舟山和太行山的知名河流,这条河流的流域面积达到了2.73万平方公里,其发源地处于山西省繁峙县泰戏山桥儿沟村,这条河流早在《山海经》中就有出现过,被叫做为虔池.为了估算河流的宽度,我们在河的对岸选定一个目标P,在近岸取点A和C,使点P、A、C共线且与河垂直,接着在过点C且与直线PC垂直的直线上选择适当的点D,确定PD与过点A且与PC垂直的直线交点B,测得AC=50m,CD=120m,AB=80m,请根据这些数据求河的宽度PA.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】C
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】
10.【答案】
11.【答案】12
12.【答案】∠ABD=∠C(答案不唯一)
13.【答案】8
14.【答案】2或5-
15.【答案】2
16.【答案】
17.【答案】(1)解:∵线段,线段c是线段a、b的比例中项,
∴,
∴(负值舍去);
(2)解:∵,
∴可设,
∴.
18.【答案】(1)略
(2)解:4:5
19.【答案】(1)证明:∵四边形ABCD是平行四边形,∴,,,
∵,∴,,∵,
∴,∵,∴;
(2)解:①∵,∴,∴,
∴,∴,∴,∴,
∵,∴四边形AOED是平行四边形,∴且,
∵四边形ABCD是平行四边形,∴且,
∴且,∴四边形BCEO是平行四边形,
∵,∴四边形OBCE为菱形.
②∵,∴,∵,∴,
∵且,∴,
∵,,∴,
∴,∴,
整理得:,∴(舍去)或,
∴,∵,∴.
20.【答案】(1)证明:∵∠BAD=90°,E为BD的中点,
∴AE=DE=BD,
∵CF=BD,
∴AE=CF=DE,
∵CF∥AE,∴四边形AECF是平行四边形,
∵∠BCD=90°,E为BD的中点,∴CE=BD,
∴AE=CE,
∴四边形AECF为菱形;
(2)∵四边形AECF为菱形,
∴AD∥CE,
∴∠ADE=∠DEC,
∵∠DCG=∠DEC,∴∠ADE=∠DCG,
∵AE∥CF,∴∠EAD=∠CFD,∴△ADE∽△FCD,
∴∴CF DE=AD CD,
∵AE=CF=DE,∴AE2=AD DC.
21.【答案】(1)解:如图,连接OC,
,
,
,
,
是⊙O的切线,
,
,
平分
(2)解:如图,连接OG,作,
,
,
,,
,,
,
,
,
,
,
,
,
,
,
,
设,,
,
,
.
22.【答案】解:由题意得,AB⊥PC,CD⊥PC,AC=50m,CD=120m,AB=80m,
∴AB∥CD,
∴∠PAB=∠PCD,∠PBA=∠PDC,
∴△PAB∽△PCD,
∴,即,
∴,
解得PA=100,
答:PA的长为100m.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
