平行四边形性质第一课时
图片预览





文档简介
课件24张PPT。19.1.1 平行四边形的性质(1)小区的伸缩门下面的图片中,有你熟悉的哪些图形?活动1、定义:
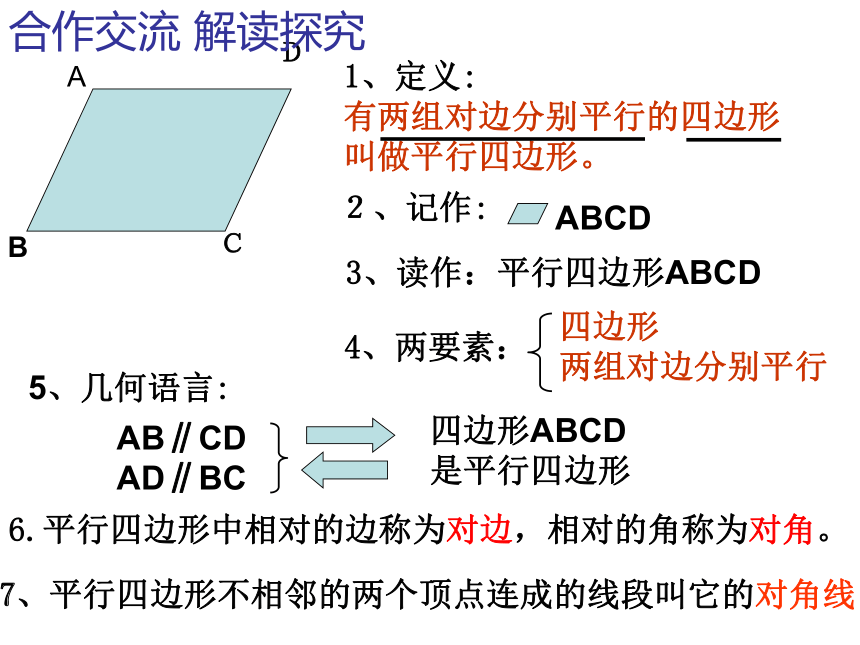
有两组对边分别平行的四边形 叫做平行四边形。2、记作:5、几何语言:
4、两要素: ABDC合作交流 解读探究四边形ABCD是平行四边形ABCD
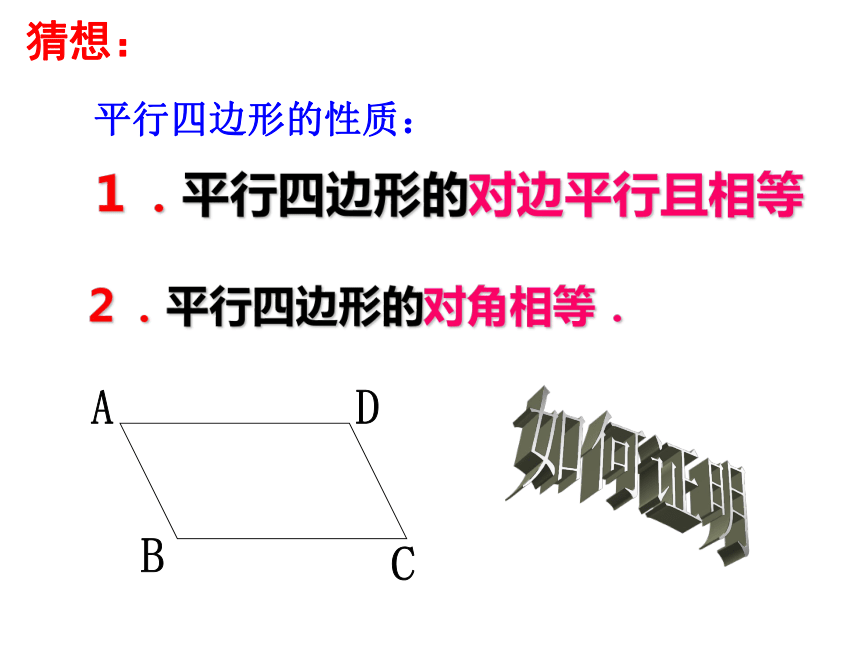
AB∥CD AD∥BC3、读作:平行四边形ABCD6.平行四边形中相对的边称为对边,相对的角称为对角。7、平行四边形不相邻的两个顶点连成的线段叫它的对角线活动二探求平行四边形的性质1、对边的关系2、对角的关系3、邻角的关系?讨 论 ? 1.平行四边形的边具有哪些性质?说说你的理由。2.平行四边形的角具有哪些性质?说说你的理由。1.平行四边形的对边平行且相等猜想:平行四边形的性质:2.平行四边形的对角相等.
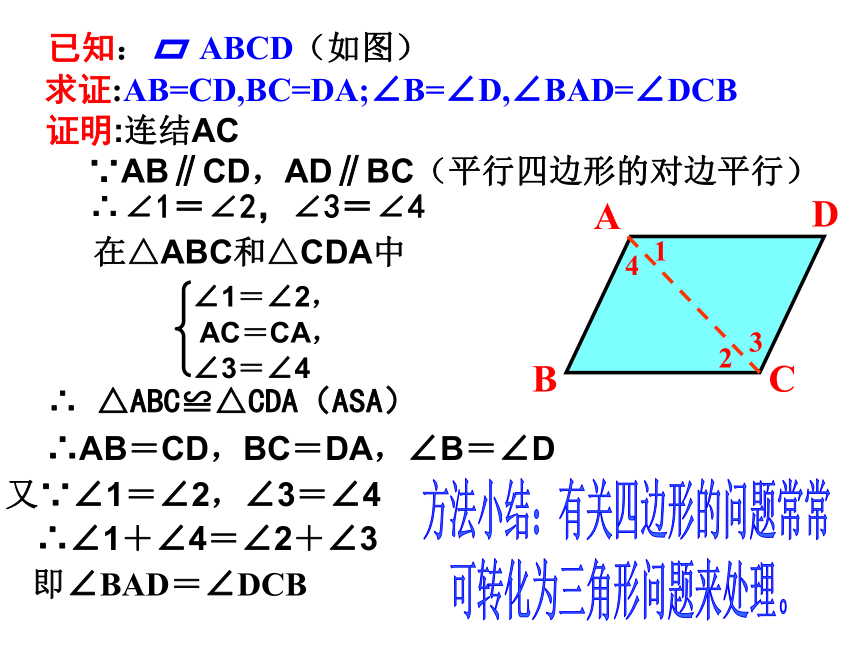
如何证明即∠BAD=∠DCB证明:连结AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∴ △ABC≌△CDA(ASA)∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在△ABC和△CDA中ABCD求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB方法小结:有关四边形的问题常常
可转化为三角形问题来处理。平行四边形的邻角互补.ABCD平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;
∵四边形ABCD是平行四边形∵四边形ABCD是平行四边形平行四边形的对边平行;∵四边形ABCD是平行四边形AB∥CD,AD∥BC小结:平行四边形的性质是证明线段相等和 角相等的重要依据和方法。平行四边形的性质平行且相等相等互补∠A=∠C,∠B=∠D∠A+∠B=180°32cm30cm56°124°124° 小试牛刀:小结:平行四边形中知道其中一角可求出另外三个角的度数。 例题教学: ? 例1 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形∵AB=8随堂练习: ? 4030120°120°60°120°40°解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm学以致用通过本节课的学习,你有什么收获?1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。课堂小结1.如图,若BE平分∠ABC,则ED= .4cm5cm5cm4cm好题大家练已知 ABCD,延长AB到E, 延长CD到F ,使BE=DF
求证:AF=CEABDCFE 如图 在?ABC中,AD平分∠BAC,点M,E,F分别
是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM
BDCEFAM 证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BAC
∴∠BAD=∠CAD
∵AB//EF ∴ ∠BAD=∠AEF
∴∠CAD =∠AEF ∴ AF=EF
∴ AF=BM例题讲解:(多变题)
如图所示,□ABCD中,E是BC的中点,连接AE并延长交DC的延长线于F,则AB与CF相等吗?说明理由
(1)一变:C是DF的中点吗?
(2)二变:若使∠F=∠DAF,□ABCD的边长之间还需要再添加一个什么条件?请你补上这个条件,并进行证明(不增添辅助线)
(3)三变:若AF平分∠DAB,且∠D=∠F,能求出∠B的度数吗?
(4)四变:若在□ABCD中,延长DC到F使DC=CF,连接AF交BC于点E,则E是BC的中点吗?
有两组对边分别平行的四边形 叫做平行四边形。2、记作:5、几何语言:
4、两要素: ABDC合作交流 解读探究四边形ABCD是平行四边形ABCD
AB∥CD AD∥BC3、读作:平行四边形ABCD6.平行四边形中相对的边称为对边,相对的角称为对角。7、平行四边形不相邻的两个顶点连成的线段叫它的对角线活动二探求平行四边形的性质1、对边的关系2、对角的关系3、邻角的关系?讨 论 ? 1.平行四边形的边具有哪些性质?说说你的理由。2.平行四边形的角具有哪些性质?说说你的理由。1.平行四边形的对边平行且相等猜想:平行四边形的性质:2.平行四边形的对角相等.
如何证明即∠BAD=∠DCB证明:连结AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∴ △ABC≌△CDA(ASA)∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在△ABC和△CDA中ABCD求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB方法小结:有关四边形的问题常常
可转化为三角形问题来处理。平行四边形的邻角互补.ABCD平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;
∵四边形ABCD是平行四边形∵四边形ABCD是平行四边形平行四边形的对边平行;∵四边形ABCD是平行四边形AB∥CD,AD∥BC小结:平行四边形的性质是证明线段相等和 角相等的重要依据和方法。平行四边形的性质平行且相等相等互补∠A=∠C,∠B=∠D∠A+∠B=180°32cm30cm56°124°124° 小试牛刀:小结:平行四边形中知道其中一角可求出另外三个角的度数。 例题教学: ? 例1 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形∵AB=8随堂练习: ? 4030120°120°60°120°40°解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm学以致用通过本节课的学习,你有什么收获?1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。课堂小结1.如图,若BE平分∠ABC,则ED= .4cm5cm5cm4cm好题大家练已知 ABCD,延长AB到E, 延长CD到F ,使BE=DF
求证:AF=CEABDCFE 如图 在?ABC中,AD平分∠BAC,点M,E,F分别
是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM
BDCEFAM 证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BAC
∴∠BAD=∠CAD
∵AB//EF ∴ ∠BAD=∠AEF
∴∠CAD =∠AEF ∴ AF=EF
∴ AF=BM例题讲解:(多变题)
如图所示,□ABCD中,E是BC的中点,连接AE并延长交DC的延长线于F,则AB与CF相等吗?说明理由
(1)一变:C是DF的中点吗?
(2)二变:若使∠F=∠DAF,□ABCD的边长之间还需要再添加一个什么条件?请你补上这个条件,并进行证明(不增添辅助线)
(3)三变:若AF平分∠DAB,且∠D=∠F,能求出∠B的度数吗?
(4)四变:若在□ABCD中,延长DC到F使DC=CF,连接AF交BC于点E,则E是BC的中点吗?
