备战2024届广东新高考数学仿真模拟练习卷(二)(新结构)(含解析)
文档属性
| 名称 | 备战2024届广东新高考数学仿真模拟练习卷(二)(新结构)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-08 21:48:48 | ||
图片预览




文档简介
备战2024年广东新高考数学仿真模拟练习卷(二)(新结构)
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑-.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( )
A. B. C. D.
2.已知复数,则( )
A. B. C. D.
3.已知表示两条直线,表示平面,下列命题中正确的有( )
①若,且,则;
②若相交且都在平面外,,则;
③若,则;
④若,且,则.
A.1个 B.2个 C.3个 D.4个
4.记是等差数列的前项和,则“是递增数列”是“是递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.加强学生心理健康工作已经上升为国家战略,为响应国家号召,W区心理协会派遣具有社会心理工作资格的3位专家去定点帮助5名心理特异学生.若要求每名学生只需一位专家负责,每位专家至多帮助两名学生,则不同的安排方法共有( )种
A.90 B.125 C.180 D.243
6.平行四边形中,,,,,则的值为( )
A.10 B.12 C.14 D.16
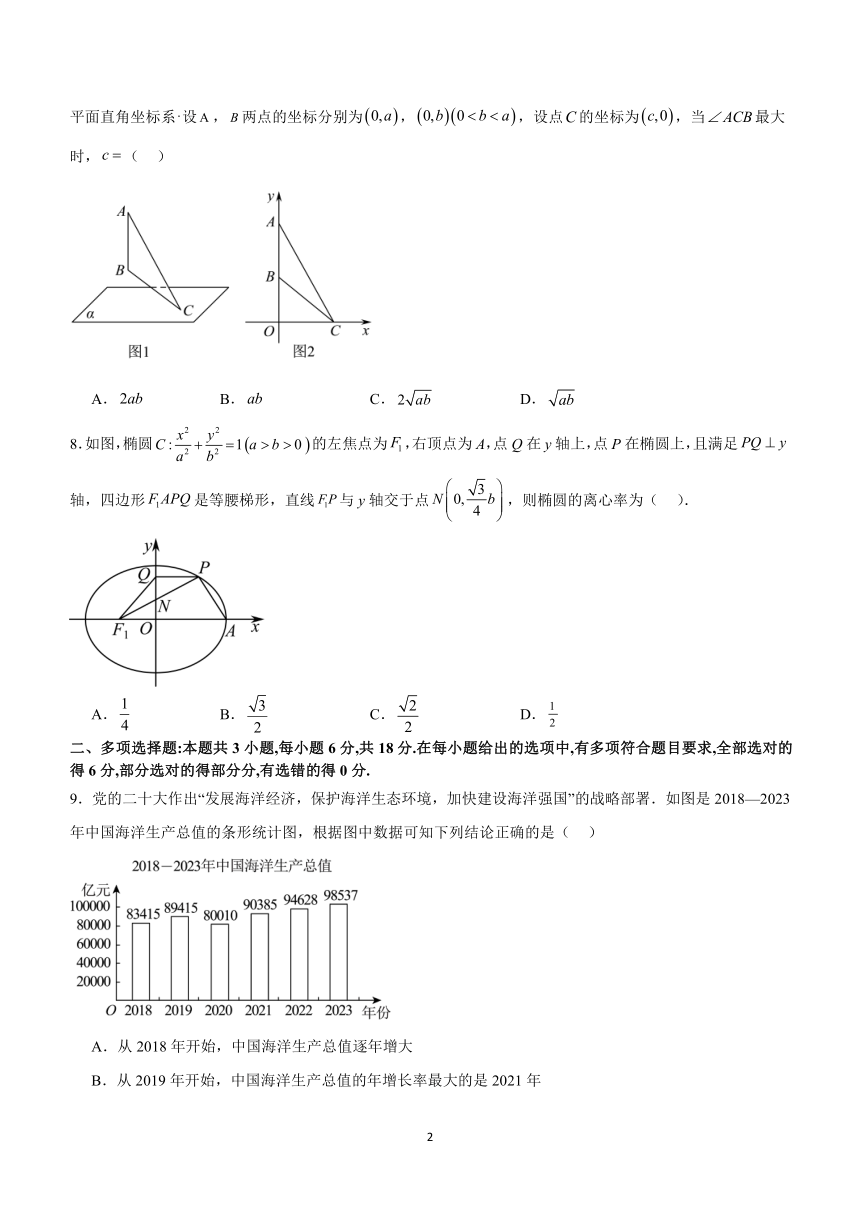
7.年米勒向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆看上去最长即可见角最大后人将其称为“米勒问题”,是载入数学史上的第一个极值问题我们把地球表面抽象为平面,悬杆抽象为线段或直线上两点,,则上述问题可以转化为如下的数学模型:如图,一条直线垂直于一个平面,直线有两点,位于平面的同侧,求平面上一点,使得最大建立如图所示的平面直角坐标系设,两点的坐标分别为,,设点的坐标为,当最大时,( )
A. B. C. D.
8.如图,椭圆的左焦点为,右顶点为A,点Q在y轴上,点P在椭圆上,且满足轴,四边形是等腰梯形,直线与y轴交于点,则椭圆的离心率为( ).
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.党的二十大作出“发展海洋经济,保护海洋生态环境,加快建设海洋强国”的战略部署.如图是2018—2023年中国海洋生产总值的条形统计图,根据图中数据可知下列结论正确的是( )
A.从2018年开始,中国海洋生产总值逐年增大
B.从2019年开始,中国海洋生产总值的年增长率最大的是2021年
C.这6年中国海洋生产总值的极差为15122
D.这6年中国海洋生产总值的80%分位数是94628
10.已知函数,下列说法正确的是( )
A.函数的值域为
B.若存在,使得对都有,则的最小值为
C.若函数在区间上单调递增,则的取值范围为
D.若函数在区间上恰有3个极值点和2个零点,则的取值范围为
11.(本题6分)已知一圆锥,其母线长为且与底面所成的角为,下列空间几何体可以被整体放入该圆锥的是( )(参考数值:,)
A.一个半径为的球
B.一个半径为与一个半径为的球
C.一个边长为且可以自由旋转的正四面体
D.一个底面在圆锥底面上,体积为的圆柱
三、填空题:本题共3小题,每小题5分,共15分.
12.已知,,若是的充分条件,则实数的取值范围是 .
13.已知圆:,若为直线:上的点,过点可作两条直线与圆分别切于点,,且为等边三角形,则实数的取值范围是 .
14.已知函数,有唯一零点,则的值为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)已知函数.
(1)若,求曲线在点处的切线方程;
(2)若,研究函数在上的单调性和零点个数.
16.(本题15分)如图,在斜三棱柱中,平面平面,,,.
(1)求证:
(2)若,求二面角的余弦值.
17.(本题15分)某地政府为推动旅游业高质量发展、加快旅游产业化建设,提出要优化传统业态,创新产品和服务方式,培育新业态新产品、新模式,促进康养旅游快速发展.某景区为了进一步优化旅游服务环境,强化服务意识,全面提升景区服务质量,准备从m个跟团游团队和6个私家游团队中随机抽取几个团队展开满意度调查.若一次抽取2个团队,全是私家游团队的概率为.
(1)若一次抽取3个团队,在抽取的3个团队是同类型团队的条件下,求这3个团队全是跟团游团队的概率;
(2)若一次抽取4个团队,设这4个团队中私家游团队的个数为,求的分布列和数学期望.
18.(本题17分)已知双曲线:(,)的一条渐近线与双曲线:的一条渐近线垂直,且的一个焦点到的一条渐近线的距离为2.
(1)求的方程;
(2)若上任意一点关于直线的对称点为,过分别作的两条渐近线的平行线,与分别交于求证:为定值.
19.(本题17分)给定整数,由元实数集合定义其相伴数集,如果,则称集合S为一个元规范数集,并定义S的范数为其中所有元素绝对值之和.
(1)判断、哪个是规范数集,并说明理由;
(2)任取一个元规范数集S,记、分别为其中最小数与最大数,求证:;
(3)当遍历所有2023元规范数集时,求范数的最小值.
注:、分别表示数集中的最小数与最大数.
备战2024年广东新高考数学仿真模拟练习卷(二)(新结构)
答案解析
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( )
A. B. C. D.
【答案】B
【分析】先解不等式求得集合B,再根据并集的概念计算即可.
【详解】由可得,即,
而,所以.
故选:B.
2.已知复数,则( )
A. B. C. D.
【答案】A
【分析】根据复数除法运算即可化简,由共轭的定义即可求解.
【详解】由得,
故,
故选:A.
3.已知表示两条直线,表示平面,下列命题中正确的有( )
①若,且,则;
②若相交且都在平面外,,则;
③若,则;
④若,且,则.
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】根据线面平行和面面平行逐项判断即可.
【详解】对于①,若,且,则或相交,故①错误;
对于③和④,与也可能相交,均错误;
对于②,设相交确定平面,根据线面平行的判定定理知,根据平行平面的传递性得知.
故选:A.
4.记是等差数列的前项和,则“是递增数列”是“是递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】C
【分析】根据等差数列的求和公式可得,即可充要条件的定义求解.
【详解】若是递增数列,则公差,所以,
故,所以为递增数列,
若为递增数列,则,则,
故,所以是递增数列,
故“是递增数列”是“是递增数列”的充要条件,
故选:C.
5.加强学生心理健康工作已经上升为国家战略,为响应国家号召,W区心理协会派遣具有社会心理工作资格的3位专家去定点帮助5名心理特异学生.若要求每名学生只需一位专家负责,每位专家至多帮助两名学生,则不同的安排方法共有( )种
A.90 B.125 C.180 D.243
【答案】A
【分析】根据已知对五位同学分3组,然后全排列即可求解.
【详解】根据题意,具有社会心理工作资格的3位专家去定点帮助5名心理特异学生,
要求每名学生只需一位专家负责,每位专家至多帮助两名学生,
则把五位同学分3组,且三组人数为2、2、1,然后分配给3位专家,
所以不同的安排方法共有种.
故选:A.
6.平行四边形中,,,,,则的值为( )
A.10 B.12 C.14 D.16
【答案】D
【分析】以作为基底,得,代入数值即可.
【详解】因为平行四边形中,,,,,
所以,
,
故选:D.
7.年米勒向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆看上去最长即可见角最大后人将其称为“米勒问题”,是载入数学史上的第一个极值问题我们把地球表面抽象为平面,悬杆抽象为线段或直线上两点,,则上述问题可以转化为如下的数学模型:如图,一条直线垂直于一个平面,直线有两点,位于平面的同侧,求平面上一点,使得最大建立如图所示的平面直角坐标系设,两点的坐标分别为,,设点的坐标为,当最大时,( )
A. B. C. D.
【答案】D
【分析】根据题意可得,然后由正切的和差角公式和基本不等式即可得到结果.
【详解】由题意可知是锐角,且,
而,
所以,
而 ,当且仅当 ,即时取等号,
因为是锐角,
所以当时,最大,此时最大.
故选:D.
8.如图,椭圆的左焦点为,右顶点为A,点Q在y轴上,点P在椭圆上,且满足轴,四边形是等腰梯形,直线与y轴交于点,则椭圆的离心率为( ).
A. B. C. D.
【答案】D
【分析】做轴于点,得到点的纵坐标,从而得到,然后根据,列出方程,即可得到结果.
【详解】
由题意,做轴于点,
因为四边形是等腰梯形,则,
则点的横坐标为,代入椭圆方程,
可得,即,
因为,则,
由,则,
化简可得,,同时除可得,
即,
对于
当时,,当时,,
在时,方程有根,
且,故应舍,所以.
故选:D.
【点睛】解答本题的关键在于得到点的纵坐标,然后根据三角形相似列出方程,得到的关系式.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.党的二十大作出“发展海洋经济,保护海洋生态环境,加快建设海洋强国”的战略部署.如图是2018—2023年中国海洋生产总值的条形统计图,根据图中数据可知下列结论正确的是( )
A.从2018年开始,中国海洋生产总值逐年增大
B.从2019年开始,中国海洋生产总值的年增长率最大的是2021年
C.这6年中国海洋生产总值的极差为15122
D.这6年中国海洋生产总值的80%分位数是94628
【答案】BD
【分析】对A,根据条形图数据可判断;对B,根据数据计算年增长率可判断;对C,计算极差可判断;对D,根据80%分位数概念计算可判断.
【详解】对于A,根据条形图数据可以看到2020年较2019年海洋生产总值是下降的,故A错误;
对于B,2019年海洋生产总值年增长率是,
2020年海洋生产总值年增长率是,2021年海洋生产总值年增长率是,
2022年海洋生产总值年增长率是,2023年海洋生产总值年增长率是,
故年增长率最大的是2021年,故B正确;
对于C,这6年中国海洋生产总值的极差为,故C错误;
对于D,将这6年的海洋生产总值按照从小到大排列80010,83415,89415,90385,94628,98537,又,
所以这6年中国海洋生产总值的80%分位数是94628,故D正确.
故选:BD.
10.已知函数,下列说法正确的是( )
A.函数的值域为
B.若存在,使得对都有,则的最小值为
C.若函数在区间上单调递增,则的取值范围为
D.若函数在区间上恰有3个极值点和2个零点,则的取值范围为
【答案】ACD
【分析】化简的解析式,根据三角函数的值域、最值、周期、单调性、极值点等知识对选项进行分析,从而确定正确答案.
【详解】已知函数,可知其值域为,故选项A正确;
若存在,使得对都有,
所以的最小值为,故选项B错误;
函数的单调递增区间为,
,
所以,令,则的取值范围为,故选项C正确;
若函数在区间上恰有3个极值点和2个零点,,
由如图可得:,
的取值范围为,故选项D正确;
故选:ACD.
11.(本题6分)已知一圆锥,其母线长为且与底面所成的角为,下列空间几何体可以被整体放入该圆锥的是( )(参考数值:,)
A.一个半径为的球
B.一个半径为与一个半径为的球
C.一个边长为且可以自由旋转的正四面体
D.一个底面在圆锥底面上,体积为的圆柱
【答案】ABC
【分析】作出相应的空间图形及轴截面,再对各个选项逐一分析判断即可得出结果.
【详解】如图1,球与圆锥侧面、底面均相切,球与球、圆锥侧面相切,
作圆锥的轴截面如图2,设小球半径为,球与边相切于点E,
,,,
所以,,
,故A正确;
设小球半径为,同理可知,故B正确;
将棱长为的正四面体放置到正方体中,如图
AI
则正四面体的外接球即正方体的外接球,易知正方体的外接球球心在体对角线的中点处,半径为的一半长,易知,,所以,
故棱长为的正四面体外接球半径为,则则边长,
,故C正确;
如图3,一圆柱内接圆锥,作圆锥的轴截面如图4,设圆柱底面半径为,高为,
因为,又易知,,代入,
整理得到,所以圆柱的体积,
令,得或,
则体积在上单调递增,在上单调递减,
,故D错误.
故选:ABC.
【点睛】关键点晴,本题的关键在于将空间问题转化成平面问题来处理.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知,,若是的充分条件,则实数的取值范围是 .
【答案】
【分析】根据分式不等式可得,由题意分析可知是的子集,根据子集关系列式求解即可.
【详解】由可得,则,解得,
即,
若是的充分条件,则是的子集,
可得,所以实数的取值范围是.
故答案为:.
13.已知圆:,若为直线:上的点,过点可作两条直线与圆分别切于点,,且为等边三角形,则实数的取值范围是 .
【答案】
【分析】求出圆心和半径,由已知条件可得,利用圆心到直线:的距离,解不等式即可求解.
【详解】由可得,所以圆心,半径,
过点可作两条直线与圆分别切于点,,且为等边三角形,
所以,所以,
圆心到直线:的距离,
解得:,
故答案为:.
14.已知函数,有唯一零点,则的值为 .
【答案】2
【分析】设,转化为方程有唯一解,即有唯一解,设,利用导数判断单调性并求出最小值可得答案.
【详解】由题意知有唯一解,,
故,
设,即,设,则,
当时,,函数单调递减,
当时,,函数单调递增;,
故方程有唯一解,即有唯一解,即有唯一解,
设,,,
当时,,函数单调递增;
当时,,函数单调递减;
当趋近于0和趋近于时,趋近于,
故只需满足,
设,,
当时,,函数单调递减,
当时,,函数单调递增,
故,故成立.
故答案为:2.
【点睛】关键点点睛:本题的解题关键点是构造函数,利用导数判断单调性
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)已知函数.
(1)若,求曲线在点处的切线方程;
(2)若,研究函数在上的单调性和零点个数.
【答案】(1);(2)在上单调递增;1
【分析】(1)当时,求出,,从而可求出切线方程.
(2)当时,利用导数求出在上单调递增.又,从而可求解.
【详解】(1)当时,,
则,则,,
所以曲线在点处的切线方程为.
(2)当时,,则,
当时,,,,则,
故在上单调递增.
又因为,所以在上的零点个数为.
16.(本题15分)如图,在斜三棱柱中,平面平面,,,.
(1)求证:
(2)若,求二面角的余弦值.
【答案】(1)详见解析;(2)
【分析】(1)根据平面平面,,得到平面,进而得到,再由,利用线面垂直的判定定理得到平面证明;
(2)结合(1)建立空间坐标系,分别求得平面的一个法向量 和平面的一个法向量,由求解.
【详解】(1)证明:因为平面平面,且平面平面,,
所以平面,又平面,
所以,又,且,
所以平面,又平面,
所以,又,
则;
(2)以O为原点,以CA,CB和的中垂线,分别为x,y,z轴,建立如图所示空间坐标系:
设,由题意得,
则,
所以,
设平面的一个法向量为: ,
则,即,
令,则,
设平面的一个法向量为,
则,即,
令,则,
所以,
所以二面角的余弦值为:.
17.(本题15分)某地政府为推动旅游业高质量发展、加快旅游产业化建设,提出要优化传统业态,创新产品和服务方式,培育新业态新产品、新模式,促进康养旅游快速发展.某景区为了进一步优化旅游服务环境,强化服务意识,全面提升景区服务质量,准备从m个跟团游团队和6个私家游团队中随机抽取几个团队展开满意度调查.若一次抽取2个团队,全是私家游团队的概率为.
(1)若一次抽取3个团队,在抽取的3个团队是同类型团队的条件下,求这3个团队全是跟团游团队的概率;
(2)若一次抽取4个团队,设这4个团队中私家游团队的个数为,求的分布列和数学期望.
【答案】(1);(2)分布列见解析,
【分析】(1)根据题意可知共有个团队,根据全是私家游团队的概率结合古典概型求出,再分3个团队全是私家游团队和3个团队全是跟团游团队两种情况讨论,结合古典概型即可得解;
(2)先写出随机变量的所有可能取值,再求出对应随机变量的概率,从而可得分布列,再根据期望公式求期望即可.
【详解】(1)由题意知共有个团队,
一次抽取2个团队的情况有种,其中全是私家游团队的情况有种,
故一次抽取2个团队,全是私家游团队的概率是,
整理得,解得或(舍去),
若一次抽取的3个团队全是私家游团队,则共有种情况,
若一次抽取的3个团队全是跟团游团队,则共有种情况,
所以在抽取的3个团队是同类型团队的条件下,
这3个团队全是跟团游团队的概率为;
(2)由题意知,随机变量的所有可能取值为0,1,2,3,4,
,,
,,
,
故的分布列为
0 1 2 3 4
P
数学期望.
18.(本题17分)已知双曲线:(,)的一条渐近线与双曲线:的一条渐近线垂直,且的一个焦点到的一条渐近线的距离为2.
(1)求的方程;
(2)若上任意一点关于直线的对称点为,过分别作的两条渐近线的平行线,与分别交于求证:为定值.
【答案】(1);(2)见解析
【分析】(1)结合题意,利用渐近线之间的关系找到,再利用点F到双曲线的一条渐近线的距离,求出即可;
(2)分别将直线的方程,直线的方程与联立,结合弦长公式表示出,化简即可证明为定值.
【详解】(1)由双曲线:可得其中一条渐近线的方程为,
因为双曲线的一条渐近线与双曲线的一条渐近线垂直,
所以双曲线的一条渐近线的方程为,
所以,即,
所以,所以的一个焦点为,
点F到双曲线的一条渐近线的距离为,
所以,故的方程为.
(2)设,则,即,,
由题意上任意一点关于直线的对称点为,得,
设,,由题意直线与的渐近线的平行,故的斜率为,
则直线的方程为,与,
联立得,
直线的方程为,与,
联立得,
所以,
故为定值.
【点睛】关键点点睛:当过圆锥曲线上一点或平面上的一点作一条直线与圆锥曲线相交时,可以联立方程,当该点特殊时,利用韦达定理快速求出另一交点坐标,有了交点坐标,计算起来会更加方便快捷,不需要韦达定理来解题.
19.(本题17分)给定整数,由元实数集合定义其相伴数集,如果,则称集合S为一个元规范数集,并定义S的范数为其中所有元素绝对值之和.
(1)判断、哪个是规范数集,并说明理由;
(2)任取一个元规范数集S,记、分别为其中最小数与最大数,求证:;
(3)当遍历所有2023元规范数集时,求范数的最小值.
注:、分别表示数集中的最小数与最大数.
【答案】(1)集合A不是规范数集;集合B是规范数集;(2)见见解析;(3)
【分析】(1)根据元规范数集的定义,只需判断集合中的元素两两相减的差的绝对值,是否都大于等于1即可;
(2)利用元规范数集的定义,得到,从而分类讨论、与三种情况,结合去绝对值的方法即可证明;
(3)法一:当时,证得,从而得到;当时,证得,从而得到;当时,分类讨论与两种情况,推得,由此得解;
法二:利用规范数集的性质与(2)中结论即可得解.
【详解】(1)对于集合A:因为,所以集合A不是规范数集;
对于集合B:因为,
又,,,,,,
所以B相伴数集,即,故集合B是规范数集.
(2)不妨设集合S中的元素为,即,
因为S为规范数集,则,则,且,使得,
当时,
则,
当且仅当且时,等号成立;
当时,
则,
当且仅当且时,等号成立;
当时,
则,
当且仅当时,等号成立;
综上所述:.
(3)法一:
不妨设,
因为S为规范数集,则,则,且,使得,
当时,
则当时,可得,
当且仅当时,等号成立,
则范数,
当且仅当时,等号成立,
又,
当且仅当时,等号成立,
故,即范数的最小值;
当时,
则当时,可得,
当且仅当时,等号成立,则,
则范数,
当且仅当时,等号成立,
又,
当且仅当时,等号成立,
故,即范数的最小值;
当,使得,且,
当,即,即时,
则当时,可得,
当且仅当时,等号成立,
则当时,可得,
当且仅当时,等号成立,
则范数
;
对于,其开口向上,对称轴为,
所以,
所以范数的最小值为;
当,即,即时,
则当时,可得,
当且仅当时,等号成立,
则当时,可得,
当且仅当时,等号成立,
则范数
;
对于,其开口向上,对称轴为,
所以,
所以范数;
综上所述:范数的最小值.
法二:
不妨设,
因为S为规范数集,则,则,且,使得,
所以对于,同样有,则,
由(2)的证明过程与结论可得,,当且仅当时,等号成立,
即,,……,
所以范数
,
当且仅当时,等号成立,
所以范数的最小值.
【点睛】关键点睛:本题解决的关键是理解元规范数集的定义,得到,再将集合中的元素进行从小到大排列,利用分类与整合的思想进行讨论分析,从而得解.
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑-.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( )
A. B. C. D.
2.已知复数,则( )
A. B. C. D.
3.已知表示两条直线,表示平面,下列命题中正确的有( )
①若,且,则;
②若相交且都在平面外,,则;
③若,则;
④若,且,则.
A.1个 B.2个 C.3个 D.4个
4.记是等差数列的前项和,则“是递增数列”是“是递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.加强学生心理健康工作已经上升为国家战略,为响应国家号召,W区心理协会派遣具有社会心理工作资格的3位专家去定点帮助5名心理特异学生.若要求每名学生只需一位专家负责,每位专家至多帮助两名学生,则不同的安排方法共有( )种
A.90 B.125 C.180 D.243
6.平行四边形中,,,,,则的值为( )
A.10 B.12 C.14 D.16
7.年米勒向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆看上去最长即可见角最大后人将其称为“米勒问题”,是载入数学史上的第一个极值问题我们把地球表面抽象为平面,悬杆抽象为线段或直线上两点,,则上述问题可以转化为如下的数学模型:如图,一条直线垂直于一个平面,直线有两点,位于平面的同侧,求平面上一点,使得最大建立如图所示的平面直角坐标系设,两点的坐标分别为,,设点的坐标为,当最大时,( )
A. B. C. D.
8.如图,椭圆的左焦点为,右顶点为A,点Q在y轴上,点P在椭圆上,且满足轴,四边形是等腰梯形,直线与y轴交于点,则椭圆的离心率为( ).
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.党的二十大作出“发展海洋经济,保护海洋生态环境,加快建设海洋强国”的战略部署.如图是2018—2023年中国海洋生产总值的条形统计图,根据图中数据可知下列结论正确的是( )
A.从2018年开始,中国海洋生产总值逐年增大
B.从2019年开始,中国海洋生产总值的年增长率最大的是2021年
C.这6年中国海洋生产总值的极差为15122
D.这6年中国海洋生产总值的80%分位数是94628
10.已知函数,下列说法正确的是( )
A.函数的值域为
B.若存在,使得对都有,则的最小值为
C.若函数在区间上单调递增,则的取值范围为
D.若函数在区间上恰有3个极值点和2个零点,则的取值范围为
11.(本题6分)已知一圆锥,其母线长为且与底面所成的角为,下列空间几何体可以被整体放入该圆锥的是( )(参考数值:,)
A.一个半径为的球
B.一个半径为与一个半径为的球
C.一个边长为且可以自由旋转的正四面体
D.一个底面在圆锥底面上,体积为的圆柱
三、填空题:本题共3小题,每小题5分,共15分.
12.已知,,若是的充分条件,则实数的取值范围是 .
13.已知圆:,若为直线:上的点,过点可作两条直线与圆分别切于点,,且为等边三角形,则实数的取值范围是 .
14.已知函数,有唯一零点,则的值为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)已知函数.
(1)若,求曲线在点处的切线方程;
(2)若,研究函数在上的单调性和零点个数.
16.(本题15分)如图,在斜三棱柱中,平面平面,,,.
(1)求证:
(2)若,求二面角的余弦值.
17.(本题15分)某地政府为推动旅游业高质量发展、加快旅游产业化建设,提出要优化传统业态,创新产品和服务方式,培育新业态新产品、新模式,促进康养旅游快速发展.某景区为了进一步优化旅游服务环境,强化服务意识,全面提升景区服务质量,准备从m个跟团游团队和6个私家游团队中随机抽取几个团队展开满意度调查.若一次抽取2个团队,全是私家游团队的概率为.
(1)若一次抽取3个团队,在抽取的3个团队是同类型团队的条件下,求这3个团队全是跟团游团队的概率;
(2)若一次抽取4个团队,设这4个团队中私家游团队的个数为,求的分布列和数学期望.
18.(本题17分)已知双曲线:(,)的一条渐近线与双曲线:的一条渐近线垂直,且的一个焦点到的一条渐近线的距离为2.
(1)求的方程;
(2)若上任意一点关于直线的对称点为,过分别作的两条渐近线的平行线,与分别交于求证:为定值.
19.(本题17分)给定整数,由元实数集合定义其相伴数集,如果,则称集合S为一个元规范数集,并定义S的范数为其中所有元素绝对值之和.
(1)判断、哪个是规范数集,并说明理由;
(2)任取一个元规范数集S,记、分别为其中最小数与最大数,求证:;
(3)当遍历所有2023元规范数集时,求范数的最小值.
注:、分别表示数集中的最小数与最大数.
备战2024年广东新高考数学仿真模拟练习卷(二)(新结构)
答案解析
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( )
A. B. C. D.
【答案】B
【分析】先解不等式求得集合B,再根据并集的概念计算即可.
【详解】由可得,即,
而,所以.
故选:B.
2.已知复数,则( )
A. B. C. D.
【答案】A
【分析】根据复数除法运算即可化简,由共轭的定义即可求解.
【详解】由得,
故,
故选:A.
3.已知表示两条直线,表示平面,下列命题中正确的有( )
①若,且,则;
②若相交且都在平面外,,则;
③若,则;
④若,且,则.
A.1个 B.2个 C.3个 D.4个
【答案】A
【分析】根据线面平行和面面平行逐项判断即可.
【详解】对于①,若,且,则或相交,故①错误;
对于③和④,与也可能相交,均错误;
对于②,设相交确定平面,根据线面平行的判定定理知,根据平行平面的传递性得知.
故选:A.
4.记是等差数列的前项和,则“是递增数列”是“是递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】C
【分析】根据等差数列的求和公式可得,即可充要条件的定义求解.
【详解】若是递增数列,则公差,所以,
故,所以为递增数列,
若为递增数列,则,则,
故,所以是递增数列,
故“是递增数列”是“是递增数列”的充要条件,
故选:C.
5.加强学生心理健康工作已经上升为国家战略,为响应国家号召,W区心理协会派遣具有社会心理工作资格的3位专家去定点帮助5名心理特异学生.若要求每名学生只需一位专家负责,每位专家至多帮助两名学生,则不同的安排方法共有( )种
A.90 B.125 C.180 D.243
【答案】A
【分析】根据已知对五位同学分3组,然后全排列即可求解.
【详解】根据题意,具有社会心理工作资格的3位专家去定点帮助5名心理特异学生,
要求每名学生只需一位专家负责,每位专家至多帮助两名学生,
则把五位同学分3组,且三组人数为2、2、1,然后分配给3位专家,
所以不同的安排方法共有种.
故选:A.
6.平行四边形中,,,,,则的值为( )
A.10 B.12 C.14 D.16
【答案】D
【分析】以作为基底,得,代入数值即可.
【详解】因为平行四边形中,,,,,
所以,
,
故选:D.
7.年米勒向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆看上去最长即可见角最大后人将其称为“米勒问题”,是载入数学史上的第一个极值问题我们把地球表面抽象为平面,悬杆抽象为线段或直线上两点,,则上述问题可以转化为如下的数学模型:如图,一条直线垂直于一个平面,直线有两点,位于平面的同侧,求平面上一点,使得最大建立如图所示的平面直角坐标系设,两点的坐标分别为,,设点的坐标为,当最大时,( )
A. B. C. D.
【答案】D
【分析】根据题意可得,然后由正切的和差角公式和基本不等式即可得到结果.
【详解】由题意可知是锐角,且,
而,
所以,
而 ,当且仅当 ,即时取等号,
因为是锐角,
所以当时,最大,此时最大.
故选:D.
8.如图,椭圆的左焦点为,右顶点为A,点Q在y轴上,点P在椭圆上,且满足轴,四边形是等腰梯形,直线与y轴交于点,则椭圆的离心率为( ).
A. B. C. D.
【答案】D
【分析】做轴于点,得到点的纵坐标,从而得到,然后根据,列出方程,即可得到结果.
【详解】
由题意,做轴于点,
因为四边形是等腰梯形,则,
则点的横坐标为,代入椭圆方程,
可得,即,
因为,则,
由,则,
化简可得,,同时除可得,
即,
对于
当时,,当时,,
在时,方程有根,
且,故应舍,所以.
故选:D.
【点睛】解答本题的关键在于得到点的纵坐标,然后根据三角形相似列出方程,得到的关系式.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.党的二十大作出“发展海洋经济,保护海洋生态环境,加快建设海洋强国”的战略部署.如图是2018—2023年中国海洋生产总值的条形统计图,根据图中数据可知下列结论正确的是( )
A.从2018年开始,中国海洋生产总值逐年增大
B.从2019年开始,中国海洋生产总值的年增长率最大的是2021年
C.这6年中国海洋生产总值的极差为15122
D.这6年中国海洋生产总值的80%分位数是94628
【答案】BD
【分析】对A,根据条形图数据可判断;对B,根据数据计算年增长率可判断;对C,计算极差可判断;对D,根据80%分位数概念计算可判断.
【详解】对于A,根据条形图数据可以看到2020年较2019年海洋生产总值是下降的,故A错误;
对于B,2019年海洋生产总值年增长率是,
2020年海洋生产总值年增长率是,2021年海洋生产总值年增长率是,
2022年海洋生产总值年增长率是,2023年海洋生产总值年增长率是,
故年增长率最大的是2021年,故B正确;
对于C,这6年中国海洋生产总值的极差为,故C错误;
对于D,将这6年的海洋生产总值按照从小到大排列80010,83415,89415,90385,94628,98537,又,
所以这6年中国海洋生产总值的80%分位数是94628,故D正确.
故选:BD.
10.已知函数,下列说法正确的是( )
A.函数的值域为
B.若存在,使得对都有,则的最小值为
C.若函数在区间上单调递增,则的取值范围为
D.若函数在区间上恰有3个极值点和2个零点,则的取值范围为
【答案】ACD
【分析】化简的解析式,根据三角函数的值域、最值、周期、单调性、极值点等知识对选项进行分析,从而确定正确答案.
【详解】已知函数,可知其值域为,故选项A正确;
若存在,使得对都有,
所以的最小值为,故选项B错误;
函数的单调递增区间为,
,
所以,令,则的取值范围为,故选项C正确;
若函数在区间上恰有3个极值点和2个零点,,
由如图可得:,
的取值范围为,故选项D正确;
故选:ACD.
11.(本题6分)已知一圆锥,其母线长为且与底面所成的角为,下列空间几何体可以被整体放入该圆锥的是( )(参考数值:,)
A.一个半径为的球
B.一个半径为与一个半径为的球
C.一个边长为且可以自由旋转的正四面体
D.一个底面在圆锥底面上,体积为的圆柱
【答案】ABC
【分析】作出相应的空间图形及轴截面,再对各个选项逐一分析判断即可得出结果.
【详解】如图1,球与圆锥侧面、底面均相切,球与球、圆锥侧面相切,
作圆锥的轴截面如图2,设小球半径为,球与边相切于点E,
,,,
所以,,
,故A正确;
设小球半径为,同理可知,故B正确;
将棱长为的正四面体放置到正方体中,如图
AI
则正四面体的外接球即正方体的外接球,易知正方体的外接球球心在体对角线的中点处,半径为的一半长,易知,,所以,
故棱长为的正四面体外接球半径为,则则边长,
,故C正确;
如图3,一圆柱内接圆锥,作圆锥的轴截面如图4,设圆柱底面半径为,高为,
因为,又易知,,代入,
整理得到,所以圆柱的体积,
令,得或,
则体积在上单调递增,在上单调递减,
,故D错误.
故选:ABC.
【点睛】关键点晴,本题的关键在于将空间问题转化成平面问题来处理.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知,,若是的充分条件,则实数的取值范围是 .
【答案】
【分析】根据分式不等式可得,由题意分析可知是的子集,根据子集关系列式求解即可.
【详解】由可得,则,解得,
即,
若是的充分条件,则是的子集,
可得,所以实数的取值范围是.
故答案为:.
13.已知圆:,若为直线:上的点,过点可作两条直线与圆分别切于点,,且为等边三角形,则实数的取值范围是 .
【答案】
【分析】求出圆心和半径,由已知条件可得,利用圆心到直线:的距离,解不等式即可求解.
【详解】由可得,所以圆心,半径,
过点可作两条直线与圆分别切于点,,且为等边三角形,
所以,所以,
圆心到直线:的距离,
解得:,
故答案为:.
14.已知函数,有唯一零点,则的值为 .
【答案】2
【分析】设,转化为方程有唯一解,即有唯一解,设,利用导数判断单调性并求出最小值可得答案.
【详解】由题意知有唯一解,,
故,
设,即,设,则,
当时,,函数单调递减,
当时,,函数单调递增;,
故方程有唯一解,即有唯一解,即有唯一解,
设,,,
当时,,函数单调递增;
当时,,函数单调递减;
当趋近于0和趋近于时,趋近于,
故只需满足,
设,,
当时,,函数单调递减,
当时,,函数单调递增,
故,故成立.
故答案为:2.
【点睛】关键点点睛:本题的解题关键点是构造函数,利用导数判断单调性
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)已知函数.
(1)若,求曲线在点处的切线方程;
(2)若,研究函数在上的单调性和零点个数.
【答案】(1);(2)在上单调递增;1
【分析】(1)当时,求出,,从而可求出切线方程.
(2)当时,利用导数求出在上单调递增.又,从而可求解.
【详解】(1)当时,,
则,则,,
所以曲线在点处的切线方程为.
(2)当时,,则,
当时,,,,则,
故在上单调递增.
又因为,所以在上的零点个数为.
16.(本题15分)如图,在斜三棱柱中,平面平面,,,.
(1)求证:
(2)若,求二面角的余弦值.
【答案】(1)详见解析;(2)
【分析】(1)根据平面平面,,得到平面,进而得到,再由,利用线面垂直的判定定理得到平面证明;
(2)结合(1)建立空间坐标系,分别求得平面的一个法向量 和平面的一个法向量,由求解.
【详解】(1)证明:因为平面平面,且平面平面,,
所以平面,又平面,
所以,又,且,
所以平面,又平面,
所以,又,
则;
(2)以O为原点,以CA,CB和的中垂线,分别为x,y,z轴,建立如图所示空间坐标系:
设,由题意得,
则,
所以,
设平面的一个法向量为: ,
则,即,
令,则,
设平面的一个法向量为,
则,即,
令,则,
所以,
所以二面角的余弦值为:.
17.(本题15分)某地政府为推动旅游业高质量发展、加快旅游产业化建设,提出要优化传统业态,创新产品和服务方式,培育新业态新产品、新模式,促进康养旅游快速发展.某景区为了进一步优化旅游服务环境,强化服务意识,全面提升景区服务质量,准备从m个跟团游团队和6个私家游团队中随机抽取几个团队展开满意度调查.若一次抽取2个团队,全是私家游团队的概率为.
(1)若一次抽取3个团队,在抽取的3个团队是同类型团队的条件下,求这3个团队全是跟团游团队的概率;
(2)若一次抽取4个团队,设这4个团队中私家游团队的个数为,求的分布列和数学期望.
【答案】(1);(2)分布列见解析,
【分析】(1)根据题意可知共有个团队,根据全是私家游团队的概率结合古典概型求出,再分3个团队全是私家游团队和3个团队全是跟团游团队两种情况讨论,结合古典概型即可得解;
(2)先写出随机变量的所有可能取值,再求出对应随机变量的概率,从而可得分布列,再根据期望公式求期望即可.
【详解】(1)由题意知共有个团队,
一次抽取2个团队的情况有种,其中全是私家游团队的情况有种,
故一次抽取2个团队,全是私家游团队的概率是,
整理得,解得或(舍去),
若一次抽取的3个团队全是私家游团队,则共有种情况,
若一次抽取的3个团队全是跟团游团队,则共有种情况,
所以在抽取的3个团队是同类型团队的条件下,
这3个团队全是跟团游团队的概率为;
(2)由题意知,随机变量的所有可能取值为0,1,2,3,4,
,,
,,
,
故的分布列为
0 1 2 3 4
P
数学期望.
18.(本题17分)已知双曲线:(,)的一条渐近线与双曲线:的一条渐近线垂直,且的一个焦点到的一条渐近线的距离为2.
(1)求的方程;
(2)若上任意一点关于直线的对称点为,过分别作的两条渐近线的平行线,与分别交于求证:为定值.
【答案】(1);(2)见解析
【分析】(1)结合题意,利用渐近线之间的关系找到,再利用点F到双曲线的一条渐近线的距离,求出即可;
(2)分别将直线的方程,直线的方程与联立,结合弦长公式表示出,化简即可证明为定值.
【详解】(1)由双曲线:可得其中一条渐近线的方程为,
因为双曲线的一条渐近线与双曲线的一条渐近线垂直,
所以双曲线的一条渐近线的方程为,
所以,即,
所以,所以的一个焦点为,
点F到双曲线的一条渐近线的距离为,
所以,故的方程为.
(2)设,则,即,,
由题意上任意一点关于直线的对称点为,得,
设,,由题意直线与的渐近线的平行,故的斜率为,
则直线的方程为,与,
联立得,
直线的方程为,与,
联立得,
所以,
故为定值.
【点睛】关键点点睛:当过圆锥曲线上一点或平面上的一点作一条直线与圆锥曲线相交时,可以联立方程,当该点特殊时,利用韦达定理快速求出另一交点坐标,有了交点坐标,计算起来会更加方便快捷,不需要韦达定理来解题.
19.(本题17分)给定整数,由元实数集合定义其相伴数集,如果,则称集合S为一个元规范数集,并定义S的范数为其中所有元素绝对值之和.
(1)判断、哪个是规范数集,并说明理由;
(2)任取一个元规范数集S,记、分别为其中最小数与最大数,求证:;
(3)当遍历所有2023元规范数集时,求范数的最小值.
注:、分别表示数集中的最小数与最大数.
【答案】(1)集合A不是规范数集;集合B是规范数集;(2)见见解析;(3)
【分析】(1)根据元规范数集的定义,只需判断集合中的元素两两相减的差的绝对值,是否都大于等于1即可;
(2)利用元规范数集的定义,得到,从而分类讨论、与三种情况,结合去绝对值的方法即可证明;
(3)法一:当时,证得,从而得到;当时,证得,从而得到;当时,分类讨论与两种情况,推得,由此得解;
法二:利用规范数集的性质与(2)中结论即可得解.
【详解】(1)对于集合A:因为,所以集合A不是规范数集;
对于集合B:因为,
又,,,,,,
所以B相伴数集,即,故集合B是规范数集.
(2)不妨设集合S中的元素为,即,
因为S为规范数集,则,则,且,使得,
当时,
则,
当且仅当且时,等号成立;
当时,
则,
当且仅当且时,等号成立;
当时,
则,
当且仅当时,等号成立;
综上所述:.
(3)法一:
不妨设,
因为S为规范数集,则,则,且,使得,
当时,
则当时,可得,
当且仅当时,等号成立,
则范数,
当且仅当时,等号成立,
又,
当且仅当时,等号成立,
故,即范数的最小值;
当时,
则当时,可得,
当且仅当时,等号成立,则,
则范数,
当且仅当时,等号成立,
又,
当且仅当时,等号成立,
故,即范数的最小值;
当,使得,且,
当,即,即时,
则当时,可得,
当且仅当时,等号成立,
则当时,可得,
当且仅当时,等号成立,
则范数
;
对于,其开口向上,对称轴为,
所以,
所以范数的最小值为;
当,即,即时,
则当时,可得,
当且仅当时,等号成立,
则当时,可得,
当且仅当时,等号成立,
则范数
;
对于,其开口向上,对称轴为,
所以,
所以范数;
综上所述:范数的最小值.
法二:
不妨设,
因为S为规范数集,则,则,且,使得,
所以对于,同样有,则,
由(2)的证明过程与结论可得,,当且仅当时,等号成立,
即,,……,
所以范数
,
当且仅当时,等号成立,
所以范数的最小值.
【点睛】关键点睛:本题解决的关键是理解元规范数集的定义,得到,再将集合中的元素进行从小到大排列,利用分类与整合的思想进行讨论分析,从而得解.
同课章节目录
