备战2024届广东新高考数学仿真模拟练习卷(三)(新结构)(含解析)
文档属性
| 名称 | 备战2024届广东新高考数学仿真模拟练习卷(三)(新结构)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-08 21:51:02 | ||
图片预览




文档简介
备战2024年广东新高考数学仿真模拟练习卷(三)(新结构)
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑-.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,集合,则图中阴影部分所表示的集合为( )
A. B. C. D.
2.已知复数在复平面内对应的点的坐标为,则下列结论正确的是( )
A. B.复数的共轭复数是
C.的实部为5 D.
3.已知向量,,若,则( )
A. B. C. D.2
4.已知在特定的时期内某人在一个月内每天投入的体育锻炼时间(分钟)与一个月内减轻的体重(斤)的一组数据如表所示:
30 40 50 60 70
一个月内减轻的体重与每天投入的体育锻炼时间之间具有较强的线性相关关系,其线性回归直线方程是,据此模型估计当此人在一个月内每天投入的体育锻炼时间为90分钟时,该月内减轻的体重约为( )
A.斤 B.斤 C.斤 D.斤
5.设函数,则( )
A.是偶函数,且在上单调递增 B.是奇函数,且在上单调递减
C.是偶函数,且在上单调递增 D.是奇函数,且在上单调递减
6.若函数在上单调,则的取值范围是( )
A. B. C. D.
7.湖南第二届旅游发展大会于2023年9月15日至17日在郴州举行,为让广大学生知晓郴州,热爱郴州,亲身感受“走遍五大洲,最美有郴州”绿色生态研学,现有甲,乙两所学校从万华岩中小学生研学实践基地,王仙岭旅游风景区,雄鹰户外基地三条线路中随机选择一条线路去研学,记事件A为“甲和乙至少有一所学校选择万华岩中小学生研学实践基地”,事件B为“甲和乙选择研学线路不同”,则( )
A. B. C. D.
8.如图,已知,是双曲线C:的左 右焦点,P,Q为双曲线C上两点,满足,且,则双曲线C的离心率为( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法中,正确的是( )
A.用简单随机抽样的方法从含有50个个体的总体中抽取一个容量为5的样本,则个体被抽到的概率是0.1
B.一组数据的第60百分位数为14
C.若样本数据的方差为8,则数据的方差为2
D.将总体划分为2层,通过分层抽样,得到两层的样本平均数和样本方差分别为,和,若,则总体方差
10.已知直线与圆总有两个不同的交点为坐标原点,则( )
A.直线过定点
B.
C.当时,
D.当时,的最小值为
11.如图,已知正方体的棱长为为底面正方形内(含边界)的一动点,则下列结论正确的是( )
A.存在点,使得平面
B.三棱锥的体积为定值
C.当点在棱上时,的最小值为
D.若点到直线与到直线的距离相等,的中点为,则点到直线的最短距离是
三、填空题:本题共3小题,每小题5分,共15分.
12.在的展开式中,的系数为 用数字作答
13.在正项等比数列中,已知,则 .
14.若对于,,使得不等式恒成立,则实数x的范围为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)年元旦将至,国产影片与国外好莱坞大片同时上映,广大网民,对喜爱的电影进行投票某平台为了解观众对影片的选择情况情况仅有“国产”“国外”,从平台所有观众中随机抽取200人进行调查,数据如下表所示单位:人
(1)把列联表补充完整,试根据小概率值的独立性检验分析对影片的选择情况是否与性别有关;
(2)若将频率视为概率,从抽取的200人中所有给出“国产”的观众中随机抽取人,用随机变量表示被抽到的女性观众的人数,求的分布列和数学期望.
国产 国外 合计
男性 40
女性 80
合计 200
参考公式:,其中.
参考数据
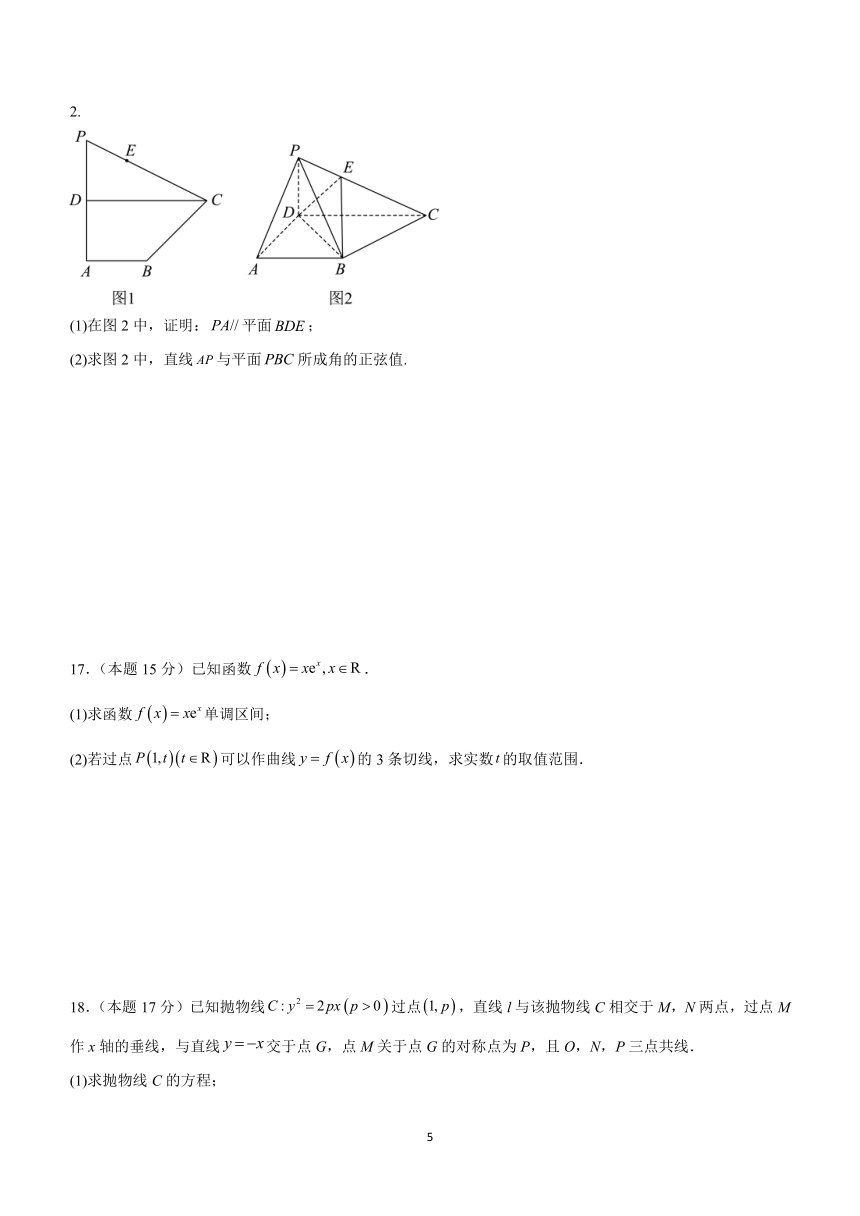
16.(本题15分)如图1,在平面四边形中,,.点是线段上靠近端的三等分点,将沿折成四棱锥,且,连接,如图2.
(1)在图2中,证明:平面;
(2)求图2中,直线与平面所成角的正弦值.
17.(本题15分)已知函数.
(1)求函数单调区间;
(2)若过点可以作曲线的3条切线,求实数的取值范围.
18.(本题17分)已知抛物线过点,直线l与该抛物线C相交于M,N两点,过点M作x轴的垂线,与直线交于点G,点M关于点G的对称点为P,且O,N,P三点共线.
(1)求抛物线C的方程;
(2)若过点作,垂足为H(不与点Q重合),是否存在定点T,使得为定值?若存在,求出该定点和该定值;若不存在,请说明理由.
19.(本题17分)对于一个有穷单调递增正整数数列P,设其各项为,,,,若数列P中存在不同的四项,,,满足,则称P为等和数列,集合称为P的一个等和子集,否则称P为不等和数列.
(1)判断下列数列是否是等和数列,若是等和数列,直接写出它的所有等和子集;A:1,3,5,7,9;B:2,4,6,7,10;
(2)已知数列P:,,,,是等和数列,并且对于任意的,总存在P的一个等和子集M满足集合,求证:数列P是等差数列;
(3)若数列P:,,,是不等和数列,求证:.
备战2024年广东新高考数学仿真模拟练习卷(三)(新结构)
答案解析
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,集合,则图中阴影部分所表示的集合为( )
A. B. C. D.
【答案】B
【分析】先化简两个集合,根据阴影部分可求答案.
【详解】由题意图中阴影部分为,
而,,
所以.
故选:B.
2.已知复数在复平面内对应的点的坐标为,则下列结论正确的是( )
A. B.复数的共轭复数是
C.的实部为5 D.
【答案】B
【分析】由复平面内对应的点,得复数,通过复数的乘法,复数模的计算,共轭复数和复数实部的定义,验证各选项的结论.
【详解】复数在复平面内对应的点的坐标为,则,
,A选项错误;
,B选项正确;
,的实部为-3,C选项错误;
,D选项错误.
故选:B.
3.已知向量,,若,则( )
A. B. C. D.2
【答案】C
【分析】直接利用向量垂直的坐标表示求解即可.
【详解】由,得,则,
故选:.
4.已知在特定的时期内某人在一个月内每天投入的体育锻炼时间(分钟)与一个月内减轻的体重(斤)的一组数据如表所示:
30 40 50 60 70
一个月内减轻的体重与每天投入的体育锻炼时间之间具有较强的线性相关关系,其线性回归直线方程是,据此模型估计当此人在一个月内每天投入的体育锻炼时间为90分钟时,该月内减轻的体重约为( )
A.斤 B.斤 C.斤 D.斤
【答案】A
【分析】先求出样本点中心,代入回归方程求出,再将代入计算即可.
【详解】由表中数据可得
,
,
将代入得,解得,
即,
则当时,.
故选:A.
5.设函数,则( )
A.是偶函数,且在上单调递增 B.是奇函数,且在上单调递减
C.是偶函数,且在上单调递增 D.是奇函数,且在上单调递减
【答案】B
【分析】根据奇偶性的定义判断函数的奇偶性,画函数图象,然后结合图象得函数的单调区间.
【详解】因为函数的定义域为R,且,
所以是奇函数,又,作出函数图象如下图:
由图知,函数在和上单调递增,在上单调递减.
故选:B.
6.若函数在上单调,则的取值范围是( )
A. B. C. D.
【答案】D
【分析】由,得到,然后根据在单调求解.
【详解】解:因为,
所以,
因为在单调,
所以,
∴,
故选:D.
7.湖南第二届旅游发展大会于2023年9月15日至17日在郴州举行,为让广大学生知晓郴州,热爱郴州,亲身感受“走遍五大洲,最美有郴州”绿色生态研学,现有甲,乙两所学校从万华岩中小学生研学实践基地,王仙岭旅游风景区,雄鹰户外基地三条线路中随机选择一条线路去研学,记事件A为“甲和乙至少有一所学校选择万华岩中小学生研学实践基地”,事件B为“甲和乙选择研学线路不同”,则( )
A. B. C. D.
【答案】B
【分析】利用古典概率求出事件的概率,再利用条件概率公式计算即得.
【详解】依题意,甲,乙随机选择一条线路去研学的试验有个基本事件,
事件A含有的基本事件数是,则,
事件含有的基本事件数为,则,
所以.
故选:B.
8.如图,已知,是双曲线C:的左 右焦点,P,Q为双曲线C上两点,满足,且,则双曲线C的离心率为( )
A. B. C. D.
【答案】B
【分析】延长与双曲线交于点P',易得,设,结合双曲线定义得,进而在中应用勾股定理得到齐次方程,即可得离心率.
【详解】延长与双曲线交于点P',因为,根据对称性知,
设,则,,可得,即,
所以,则,,
即,可知,
在中,由勾股定理得,即,解得.
故选:B.
【点睛】关键点点睛:延长与双曲线交于点P',利用双曲线对称性及定义求出,最后在中应用勾股定理得到齐次方程为关键.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法中,正确的是( )
A.用简单随机抽样的方法从含有50个个体的总体中抽取一个容量为5的样本,则个体被抽到的概率是0.1
B.一组数据的第60百分位数为14
C.若样本数据的方差为8,则数据的方差为2
D.将总体划分为2层,通过分层抽样,得到两层的样本平均数和样本方差分别为,和,若,则总体方差
【答案】AC
【分析】由古典概型的概率可判断A,根据百分位数定义可判断B,由数据的平均数和方差的定义可判断C,D.
【详解】选项A:个体m被抽到的概率为,故A正确;
选项B:由于,第六个数为14,第七个数为16,则第60百分位数为,故B错误;
选项C:设数据的平均数为,方差为,
则数据的平均数为,
方差为
,
所以,故C正确;
选项D:设第一层数据为,第二层数据为,
则,,
所以,
,,
总体平均数,
总体方差
因为,则,
所以
,故D错误.
故选:AC.
10.已知直线与圆总有两个不同的交点为坐标原点,则( )
A.直线过定点
B.
C.当时,
D.当时,的最小值为
【答案】ACD
【分析】根据直线方程求得定点判断A;利用点在圆内求得的取值范围判断B;利用弦长公式求得判断C;利用数量积运算,结合直线与圆的关系判断D.
【详解】对于A,可化为,
则直线过定点,故A正确;
对于B,因为直线与圆总有两个公共点,可得点在圆内部,
所以,解得,故B错误;
对于C,当时,圆的方程为,
所以圆心,又,则,
可得的最小值为,最大值即为,故C正确;
对于D,当时,圆的方程为,
则,
当直线过圆心时,,所以的最小值为,
所以的最小值为,故D正确.
故选:ACD.
11.如图,已知正方体的棱长为为底面正方形内(含边界)的一动点,则下列结论正确的是( )
A.存在点,使得平面
B.三棱锥的体积为定值
C.当点在棱上时,的最小值为
D.若点到直线与到直线的距离相等,的中点为,则点到直线的最短距离是
【答案】ABD
【分析】对于A选项,当点P与A重合时,利用线面垂直的判定定理即可判断;对于B选项,由P到上底面的距离是定值即可判断;对于C选项,将平面沿旋转至平面共面,即可得到的最小值,从而得以判断;对于D选项,先得到点P的轨迹方程,将问题转化为抛物线上的点到直线的最小距离,从而得解.
【详解】对于A选项,如图,连接,,
因为在正方体中,平面,平面,
所以,因为为正方形,所以,
又因为,,平面,所以平面,
因为平面,所以,同理可得,
因为,,平面,所以平面,
所以当点P与A重合时,平面,故A正确;
对于B选项,三棱锥的体积就是三棱锥的体积,而P到上底面的距离是定值,
所以三棱锥的体积是定值,故B正确;
对于C选项,当点P在棱上时,把平面沿旋转,
使得旋转面与平面共面,连接,如图,
此时取得最小值,在中,,,
则,故C错误;
对于D,由点P到直线与到直线的距离相等,
可知P在以为准线,B为焦点的抛物线上,建立如图所示的平面直角坐标系,
则,P的轨迹是抛物线,其方程为,
因为CD的中点为E,、,
所以AE的方程:,与AE平行的抛物线的切线方程设为,
联立,可得,
则由,解得,可得切线方程为,
则点P到直线AE的最短距离为,故D正确;
故选:ABD.
【点睛】本题D选项的结论的解决关键是利用抛物线的定义,建立平面直角坐标系,得到点P的轨迹方程,从而将问题转化为抛物线上的点到直线AE的距离的最值,从而得解.
三、填空题:本题共3小题,每小题5分,共15分.
12.在的展开式中,的系数为 用数字作答
【答案】
【分析】直接用二项式定理展开的通项求出即可.
【详解】在的展开式中通项为,
所以,解得,
所以的系数为,
故答案为:.
13.在正项等比数列中,已知,则 .
【答案】16
【分析】由题意得,两式相比得,再由,两式相比得,由此即可得解.
【详解】因为,所以,因为,所以,
所以,,所以,
,所以.
故答案为:16.
14.若对于,,使得不等式恒成立,则实数x的范围为 .
【答案】
【分析】由题,有.利用导数可得,则可得.
后将看成关于m的函数,后分类讨论
在三种情况下的最大值与0的大小即可.
【详解】恒成立,
等价于.
令,,则,
注意到时,,,时,.
则在上单调递减,在上单调递增,则.
则,则
.
令,.
当,,故满足条件;
当,则在上单调递减,故
.
令,.
则,得在上单调递增,
时,,因此时无最值,且,.
则不合题意;
当,在上单调递增,故
.
令.
则.
令,.
则,故在上单调递减,
则,则在上单调递增,
则,则符合题意.
综上,.
故答案为:.
【点睛】关键点点睛:本题涉及双变量与恒成立,难度较大.
恒成立问题常转化为最值相关问题,本题因告知m范围,求x范围,故还采取了变换主元的做题方法.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)年元旦将至,国产影片与国外好莱坞大片同时上映,广大网民,对喜爱的电影进行投票某平台为了解观众对影片的选择情况情况仅有“国产”“国外”,从平台所有观众中随机抽取200人进行调查,数据如下表所示单位:人
(1)把列联表补充完整,试根据小概率值的独立性检验分析对影片的选择情况是否与性别有关;
(2)若将频率视为概率,从抽取的200人中所有给出“国产”的观众中随机抽取人,用随机变量表示被抽到的女性观众的人数,求的分布列和数学期望.
国产 国外 合计
男性 40
女性 80
合计 200
参考公式:,其中.
参考数据
【答案】(1)表格见解析,有关;(2)分布列见解析,
【分析】(1)通过计算的值,查表即可判断;
(2)根据条件知,,继而可求得分布列和期望.
【详解】(1)2×2列联表补充完整如下:
国产 国外 合计
男性 60 40 100
女性 80 20 100
合计 140 60 200
零假设为:对影片的选择情况与性别无关.
根据列联表中数据,经计算得:
根据小概率值的独立性检验,推断不成立,
即认为对影片的选择情况与性别有关,此推断犯错误的概率不大于0.005.
(2)从抽取的人中所有给出“国产”的观众中随机抽取1人为女性的概率,
且各次抽取之间互相独立,故,
所以,,
,,
故X的分布列为:
X 0 1 2 3
P
所以.
16.(本题15分)如图1,在平面四边形中,,.点是线段上靠近端的三等分点,将沿折成四棱锥,且,连接,如图2.
(1)在图2中,证明:平面;
(2)求图2中,直线与平面所成角的正弦值.
【答案】(1)证明见解析;(2)
【分析】(1)根据线面平行的判定定理证得平面.
(2)建立空间直角坐标系,利用向量法求得直线与平面所成角的正弦值.
【详解】(1)连接交于点,连接,
,
平面平面平面,
(2)在图1中,,
在图2中,,
平面,平面,
平面,所以,而,
由此以点为坐标原点,建立如图所示的空间直角坐标系,
则,
设平面的法向量为,则,
可取,又,
所以,
所以直线与平面所成角的正弦值为.
17.(本题15分)已知函数.
(1)求函数单调区间;
(2)若过点可以作曲线的3条切线,求实数的取值范围.
【答案】(1)单调递增区间是;单调递减区间是;(2)
【分析】(1)求出函数的导数,解不等式,即可求得函数单调区间;
(2)设切点坐标为,利用导数的几何意义求出切线方程,推出方程有三个不等实数根,构造函数,将方程根的问题转化为函数图像的交点问题,利用导数判断函数的性质,作出函数图像,数形结合,即可求解.
【详解】(1)函数的定义域为,,
令,解得,所以函数的单调递增区间是;
令,解得,所以函数的单调递减区间是
(2)由题意可得,
设切点坐标为,则切线斜率,
所以切线方程为,
将代入得.
因为存在三条切线,即方程有三个不等实数根,
方程有三个不等实数根等价于函数的图像有三个交点,
设,则,
当时,在上单调递增;
在和上,在和上单调递减,
,;
当或时,,时,,
当时,;当时,,
画出的图象如图,
要使函数的图像有三个交点,需,
即,即实数的取值范围.
【点睛】难点点睛:解答本题的难点在于根据过点可以作曲线的3条切线,求解参数的范围,解答时要利用导数的几何意义求出切线方程,即要使得方程有三个不等实数根,构造函数,转化为函数的图像的交点问题,利用导数判断函数性质,数形结合,即可求解.
18.(本题17分)已知抛物线过点,直线l与该抛物线C相交于M,N两点,过点M作x轴的垂线,与直线交于点G,点M关于点G的对称点为P,且O,N,P三点共线.
(1)求抛物线C的方程;
(2)若过点作,垂足为H(不与点Q重合),是否存在定点T,使得为定值?若存在,求出该定点和该定值;若不存在,请说明理由.
【答案】(1);(2)存在定点,使得为定值,该定值为
【分析】(1)将点代入抛物线方程可求出,从而可求出抛物线方程;
(2)设点,,然后表示出点的坐标,由O,N,P三点共线,化简可得,设直线l的方程为,代入抛物线方程化简,利用根与系数的关系可得,则直线l过定点,从而可得点H的轨迹是以为直径的圆.
【详解】(1)因为抛物线过点,所以,所以,
所以抛物线C的方程为.
(2)设点,,联立,得,
又因为点M关于点G的对称点为P,所以点,
由O,N,P三点共线,可得,即,
化简得,
设直线l的方程为,联立,消去x,得,
则,即,可得,,
代入,可得,可得,
所以直线l的方程:,即,则,
所以直线l过定点,
因为,
所以点H的轨迹是以为直径的圆(除去E,Q两点),圆心为,半径为,
所以存在定点,使得为定值,该定值为.
.
【点睛】关键点睛:此题考查直线与抛物线的位置关系,考查抛物线中的定点问题,解题的关键是将直线方程代入抛物线方程化简,利用根与系数的关系,再结合O,N,P三点共线的条件表示出直线方程,从而可求得直线过的定点.
19.(本题17分)对于一个有穷单调递增正整数数列P,设其各项为,,,,若数列P中存在不同的四项,,,满足,则称P为等和数列,集合称为P的一个等和子集,否则称P为不等和数列.
(1)判断下列数列是否是等和数列,若是等和数列,直接写出它的所有等和子集;A:1,3,5,7,9;B:2,4,6,7,10;
(2)已知数列P:,,,,是等和数列,并且对于任意的,总存在P的一个等和子集M满足集合,求证:数列P是等差数列;
(3)若数列P:,,,是不等和数列,求证:.
【答案】(1)是等和数列,所有的等和子集为,,;不是等和数列;(2)见解析;(3)见解析
【分析】(1)由等和数列的定义判断即可;
(2)数列P最多有如下五个等和子集:,,,,,根据反证法结合等差数列的定义证明即可;
(3)假设,且不是整数,利用反证法证明即可.
【详解】(1)A是等和数列,所有的等和子集为,,;
B是不等和数列.
(2)数列P最多有如下五个等和子集:,,,,,
考虑,,只可能是如下三种情况的一种:
,,,
若,则,不是P的等和子集,
否则,或,并且不是P的等和子集,否则,,
所以,P的所有等和子集有,,
此时,不满足,该情况不成立,即;
由对称性可知,,
因此,,此时,,不是P的等和子集,
考虑,,
故,是P的等和子集,
故,,
由以上三式可知,即数列P是等差数列.
(3)假设,且不是整数,
则对于任意,总有,
因为数列P是不等和数列,所以,至少有个不同的取值,
若存在,则,,
当时,若,则,则存在等和数列,与题设矛盾,
故时,有,
所以,,只有个不同的取值,
因此,,,
又因为存在,所以,,此时,,矛盾.
若不存在,则,恰个不同的取值,
所以,,,并且,,
此时,,矛盾.
综上,.
【点睛】思路点睛:本题考查了数列新定义问题,按着某种规律新生出另一个数列的题目,涉及到归纳推理的思想方法,对学生的思维能力要求较高,综合性强,能很好的考查学生的综合素养,解答的关键是要理解新定义,根据定义进行逻辑推理,进而解决问题.
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑-.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,集合,则图中阴影部分所表示的集合为( )
A. B. C. D.
2.已知复数在复平面内对应的点的坐标为,则下列结论正确的是( )
A. B.复数的共轭复数是
C.的实部为5 D.
3.已知向量,,若,则( )
A. B. C. D.2
4.已知在特定的时期内某人在一个月内每天投入的体育锻炼时间(分钟)与一个月内减轻的体重(斤)的一组数据如表所示:
30 40 50 60 70
一个月内减轻的体重与每天投入的体育锻炼时间之间具有较强的线性相关关系,其线性回归直线方程是,据此模型估计当此人在一个月内每天投入的体育锻炼时间为90分钟时,该月内减轻的体重约为( )
A.斤 B.斤 C.斤 D.斤
5.设函数,则( )
A.是偶函数,且在上单调递增 B.是奇函数,且在上单调递减
C.是偶函数,且在上单调递增 D.是奇函数,且在上单调递减
6.若函数在上单调,则的取值范围是( )
A. B. C. D.
7.湖南第二届旅游发展大会于2023年9月15日至17日在郴州举行,为让广大学生知晓郴州,热爱郴州,亲身感受“走遍五大洲,最美有郴州”绿色生态研学,现有甲,乙两所学校从万华岩中小学生研学实践基地,王仙岭旅游风景区,雄鹰户外基地三条线路中随机选择一条线路去研学,记事件A为“甲和乙至少有一所学校选择万华岩中小学生研学实践基地”,事件B为“甲和乙选择研学线路不同”,则( )
A. B. C. D.
8.如图,已知,是双曲线C:的左 右焦点,P,Q为双曲线C上两点,满足,且,则双曲线C的离心率为( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法中,正确的是( )
A.用简单随机抽样的方法从含有50个个体的总体中抽取一个容量为5的样本,则个体被抽到的概率是0.1
B.一组数据的第60百分位数为14
C.若样本数据的方差为8,则数据的方差为2
D.将总体划分为2层,通过分层抽样,得到两层的样本平均数和样本方差分别为,和,若,则总体方差
10.已知直线与圆总有两个不同的交点为坐标原点,则( )
A.直线过定点
B.
C.当时,
D.当时,的最小值为
11.如图,已知正方体的棱长为为底面正方形内(含边界)的一动点,则下列结论正确的是( )
A.存在点,使得平面
B.三棱锥的体积为定值
C.当点在棱上时,的最小值为
D.若点到直线与到直线的距离相等,的中点为,则点到直线的最短距离是
三、填空题:本题共3小题,每小题5分,共15分.
12.在的展开式中,的系数为 用数字作答
13.在正项等比数列中,已知,则 .
14.若对于,,使得不等式恒成立,则实数x的范围为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)年元旦将至,国产影片与国外好莱坞大片同时上映,广大网民,对喜爱的电影进行投票某平台为了解观众对影片的选择情况情况仅有“国产”“国外”,从平台所有观众中随机抽取200人进行调查,数据如下表所示单位:人
(1)把列联表补充完整,试根据小概率值的独立性检验分析对影片的选择情况是否与性别有关;
(2)若将频率视为概率,从抽取的200人中所有给出“国产”的观众中随机抽取人,用随机变量表示被抽到的女性观众的人数,求的分布列和数学期望.
国产 国外 合计
男性 40
女性 80
合计 200
参考公式:,其中.
参考数据
16.(本题15分)如图1,在平面四边形中,,.点是线段上靠近端的三等分点,将沿折成四棱锥,且,连接,如图2.
(1)在图2中,证明:平面;
(2)求图2中,直线与平面所成角的正弦值.
17.(本题15分)已知函数.
(1)求函数单调区间;
(2)若过点可以作曲线的3条切线,求实数的取值范围.
18.(本题17分)已知抛物线过点,直线l与该抛物线C相交于M,N两点,过点M作x轴的垂线,与直线交于点G,点M关于点G的对称点为P,且O,N,P三点共线.
(1)求抛物线C的方程;
(2)若过点作,垂足为H(不与点Q重合),是否存在定点T,使得为定值?若存在,求出该定点和该定值;若不存在,请说明理由.
19.(本题17分)对于一个有穷单调递增正整数数列P,设其各项为,,,,若数列P中存在不同的四项,,,满足,则称P为等和数列,集合称为P的一个等和子集,否则称P为不等和数列.
(1)判断下列数列是否是等和数列,若是等和数列,直接写出它的所有等和子集;A:1,3,5,7,9;B:2,4,6,7,10;
(2)已知数列P:,,,,是等和数列,并且对于任意的,总存在P的一个等和子集M满足集合,求证:数列P是等差数列;
(3)若数列P:,,,是不等和数列,求证:.
备战2024年广东新高考数学仿真模拟练习卷(三)(新结构)
答案解析
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,集合,则图中阴影部分所表示的集合为( )
A. B. C. D.
【答案】B
【分析】先化简两个集合,根据阴影部分可求答案.
【详解】由题意图中阴影部分为,
而,,
所以.
故选:B.
2.已知复数在复平面内对应的点的坐标为,则下列结论正确的是( )
A. B.复数的共轭复数是
C.的实部为5 D.
【答案】B
【分析】由复平面内对应的点,得复数,通过复数的乘法,复数模的计算,共轭复数和复数实部的定义,验证各选项的结论.
【详解】复数在复平面内对应的点的坐标为,则,
,A选项错误;
,B选项正确;
,的实部为-3,C选项错误;
,D选项错误.
故选:B.
3.已知向量,,若,则( )
A. B. C. D.2
【答案】C
【分析】直接利用向量垂直的坐标表示求解即可.
【详解】由,得,则,
故选:.
4.已知在特定的时期内某人在一个月内每天投入的体育锻炼时间(分钟)与一个月内减轻的体重(斤)的一组数据如表所示:
30 40 50 60 70
一个月内减轻的体重与每天投入的体育锻炼时间之间具有较强的线性相关关系,其线性回归直线方程是,据此模型估计当此人在一个月内每天投入的体育锻炼时间为90分钟时,该月内减轻的体重约为( )
A.斤 B.斤 C.斤 D.斤
【答案】A
【分析】先求出样本点中心,代入回归方程求出,再将代入计算即可.
【详解】由表中数据可得
,
,
将代入得,解得,
即,
则当时,.
故选:A.
5.设函数,则( )
A.是偶函数,且在上单调递增 B.是奇函数,且在上单调递减
C.是偶函数,且在上单调递增 D.是奇函数,且在上单调递减
【答案】B
【分析】根据奇偶性的定义判断函数的奇偶性,画函数图象,然后结合图象得函数的单调区间.
【详解】因为函数的定义域为R,且,
所以是奇函数,又,作出函数图象如下图:
由图知,函数在和上单调递增,在上单调递减.
故选:B.
6.若函数在上单调,则的取值范围是( )
A. B. C. D.
【答案】D
【分析】由,得到,然后根据在单调求解.
【详解】解:因为,
所以,
因为在单调,
所以,
∴,
故选:D.
7.湖南第二届旅游发展大会于2023年9月15日至17日在郴州举行,为让广大学生知晓郴州,热爱郴州,亲身感受“走遍五大洲,最美有郴州”绿色生态研学,现有甲,乙两所学校从万华岩中小学生研学实践基地,王仙岭旅游风景区,雄鹰户外基地三条线路中随机选择一条线路去研学,记事件A为“甲和乙至少有一所学校选择万华岩中小学生研学实践基地”,事件B为“甲和乙选择研学线路不同”,则( )
A. B. C. D.
【答案】B
【分析】利用古典概率求出事件的概率,再利用条件概率公式计算即得.
【详解】依题意,甲,乙随机选择一条线路去研学的试验有个基本事件,
事件A含有的基本事件数是,则,
事件含有的基本事件数为,则,
所以.
故选:B.
8.如图,已知,是双曲线C:的左 右焦点,P,Q为双曲线C上两点,满足,且,则双曲线C的离心率为( )
A. B. C. D.
【答案】B
【分析】延长与双曲线交于点P',易得,设,结合双曲线定义得,进而在中应用勾股定理得到齐次方程,即可得离心率.
【详解】延长与双曲线交于点P',因为,根据对称性知,
设,则,,可得,即,
所以,则,,
即,可知,
在中,由勾股定理得,即,解得.
故选:B.
【点睛】关键点点睛:延长与双曲线交于点P',利用双曲线对称性及定义求出,最后在中应用勾股定理得到齐次方程为关键.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法中,正确的是( )
A.用简单随机抽样的方法从含有50个个体的总体中抽取一个容量为5的样本,则个体被抽到的概率是0.1
B.一组数据的第60百分位数为14
C.若样本数据的方差为8,则数据的方差为2
D.将总体划分为2层,通过分层抽样,得到两层的样本平均数和样本方差分别为,和,若,则总体方差
【答案】AC
【分析】由古典概型的概率可判断A,根据百分位数定义可判断B,由数据的平均数和方差的定义可判断C,D.
【详解】选项A:个体m被抽到的概率为,故A正确;
选项B:由于,第六个数为14,第七个数为16,则第60百分位数为,故B错误;
选项C:设数据的平均数为,方差为,
则数据的平均数为,
方差为
,
所以,故C正确;
选项D:设第一层数据为,第二层数据为,
则,,
所以,
,,
总体平均数,
总体方差
因为,则,
所以
,故D错误.
故选:AC.
10.已知直线与圆总有两个不同的交点为坐标原点,则( )
A.直线过定点
B.
C.当时,
D.当时,的最小值为
【答案】ACD
【分析】根据直线方程求得定点判断A;利用点在圆内求得的取值范围判断B;利用弦长公式求得判断C;利用数量积运算,结合直线与圆的关系判断D.
【详解】对于A,可化为,
则直线过定点,故A正确;
对于B,因为直线与圆总有两个公共点,可得点在圆内部,
所以,解得,故B错误;
对于C,当时,圆的方程为,
所以圆心,又,则,
可得的最小值为,最大值即为,故C正确;
对于D,当时,圆的方程为,
则,
当直线过圆心时,,所以的最小值为,
所以的最小值为,故D正确.
故选:ACD.
11.如图,已知正方体的棱长为为底面正方形内(含边界)的一动点,则下列结论正确的是( )
A.存在点,使得平面
B.三棱锥的体积为定值
C.当点在棱上时,的最小值为
D.若点到直线与到直线的距离相等,的中点为,则点到直线的最短距离是
【答案】ABD
【分析】对于A选项,当点P与A重合时,利用线面垂直的判定定理即可判断;对于B选项,由P到上底面的距离是定值即可判断;对于C选项,将平面沿旋转至平面共面,即可得到的最小值,从而得以判断;对于D选项,先得到点P的轨迹方程,将问题转化为抛物线上的点到直线的最小距离,从而得解.
【详解】对于A选项,如图,连接,,
因为在正方体中,平面,平面,
所以,因为为正方形,所以,
又因为,,平面,所以平面,
因为平面,所以,同理可得,
因为,,平面,所以平面,
所以当点P与A重合时,平面,故A正确;
对于B选项,三棱锥的体积就是三棱锥的体积,而P到上底面的距离是定值,
所以三棱锥的体积是定值,故B正确;
对于C选项,当点P在棱上时,把平面沿旋转,
使得旋转面与平面共面,连接,如图,
此时取得最小值,在中,,,
则,故C错误;
对于D,由点P到直线与到直线的距离相等,
可知P在以为准线,B为焦点的抛物线上,建立如图所示的平面直角坐标系,
则,P的轨迹是抛物线,其方程为,
因为CD的中点为E,、,
所以AE的方程:,与AE平行的抛物线的切线方程设为,
联立,可得,
则由,解得,可得切线方程为,
则点P到直线AE的最短距离为,故D正确;
故选:ABD.
【点睛】本题D选项的结论的解决关键是利用抛物线的定义,建立平面直角坐标系,得到点P的轨迹方程,从而将问题转化为抛物线上的点到直线AE的距离的最值,从而得解.
三、填空题:本题共3小题,每小题5分,共15分.
12.在的展开式中,的系数为 用数字作答
【答案】
【分析】直接用二项式定理展开的通项求出即可.
【详解】在的展开式中通项为,
所以,解得,
所以的系数为,
故答案为:.
13.在正项等比数列中,已知,则 .
【答案】16
【分析】由题意得,两式相比得,再由,两式相比得,由此即可得解.
【详解】因为,所以,因为,所以,
所以,,所以,
,所以.
故答案为:16.
14.若对于,,使得不等式恒成立,则实数x的范围为 .
【答案】
【分析】由题,有.利用导数可得,则可得.
后将看成关于m的函数,后分类讨论
在三种情况下的最大值与0的大小即可.
【详解】恒成立,
等价于.
令,,则,
注意到时,,,时,.
则在上单调递减,在上单调递增,则.
则,则
.
令,.
当,,故满足条件;
当,则在上单调递减,故
.
令,.
则,得在上单调递增,
时,,因此时无最值,且,.
则不合题意;
当,在上单调递增,故
.
令.
则.
令,.
则,故在上单调递减,
则,则在上单调递增,
则,则符合题意.
综上,.
故答案为:.
【点睛】关键点点睛:本题涉及双变量与恒成立,难度较大.
恒成立问题常转化为最值相关问题,本题因告知m范围,求x范围,故还采取了变换主元的做题方法.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题13分)年元旦将至,国产影片与国外好莱坞大片同时上映,广大网民,对喜爱的电影进行投票某平台为了解观众对影片的选择情况情况仅有“国产”“国外”,从平台所有观众中随机抽取200人进行调查,数据如下表所示单位:人
(1)把列联表补充完整,试根据小概率值的独立性检验分析对影片的选择情况是否与性别有关;
(2)若将频率视为概率,从抽取的200人中所有给出“国产”的观众中随机抽取人,用随机变量表示被抽到的女性观众的人数,求的分布列和数学期望.
国产 国外 合计
男性 40
女性 80
合计 200
参考公式:,其中.
参考数据
【答案】(1)表格见解析,有关;(2)分布列见解析,
【分析】(1)通过计算的值,查表即可判断;
(2)根据条件知,,继而可求得分布列和期望.
【详解】(1)2×2列联表补充完整如下:
国产 国外 合计
男性 60 40 100
女性 80 20 100
合计 140 60 200
零假设为:对影片的选择情况与性别无关.
根据列联表中数据,经计算得:
根据小概率值的独立性检验,推断不成立,
即认为对影片的选择情况与性别有关,此推断犯错误的概率不大于0.005.
(2)从抽取的人中所有给出“国产”的观众中随机抽取1人为女性的概率,
且各次抽取之间互相独立,故,
所以,,
,,
故X的分布列为:
X 0 1 2 3
P
所以.
16.(本题15分)如图1,在平面四边形中,,.点是线段上靠近端的三等分点,将沿折成四棱锥,且,连接,如图2.
(1)在图2中,证明:平面;
(2)求图2中,直线与平面所成角的正弦值.
【答案】(1)证明见解析;(2)
【分析】(1)根据线面平行的判定定理证得平面.
(2)建立空间直角坐标系,利用向量法求得直线与平面所成角的正弦值.
【详解】(1)连接交于点,连接,
,
平面平面平面,
(2)在图1中,,
在图2中,,
平面,平面,
平面,所以,而,
由此以点为坐标原点,建立如图所示的空间直角坐标系,
则,
设平面的法向量为,则,
可取,又,
所以,
所以直线与平面所成角的正弦值为.
17.(本题15分)已知函数.
(1)求函数单调区间;
(2)若过点可以作曲线的3条切线,求实数的取值范围.
【答案】(1)单调递增区间是;单调递减区间是;(2)
【分析】(1)求出函数的导数,解不等式,即可求得函数单调区间;
(2)设切点坐标为,利用导数的几何意义求出切线方程,推出方程有三个不等实数根,构造函数,将方程根的问题转化为函数图像的交点问题,利用导数判断函数的性质,作出函数图像,数形结合,即可求解.
【详解】(1)函数的定义域为,,
令,解得,所以函数的单调递增区间是;
令,解得,所以函数的单调递减区间是
(2)由题意可得,
设切点坐标为,则切线斜率,
所以切线方程为,
将代入得.
因为存在三条切线,即方程有三个不等实数根,
方程有三个不等实数根等价于函数的图像有三个交点,
设,则,
当时,在上单调递增;
在和上,在和上单调递减,
,;
当或时,,时,,
当时,;当时,,
画出的图象如图,
要使函数的图像有三个交点,需,
即,即实数的取值范围.
【点睛】难点点睛:解答本题的难点在于根据过点可以作曲线的3条切线,求解参数的范围,解答时要利用导数的几何意义求出切线方程,即要使得方程有三个不等实数根,构造函数,转化为函数的图像的交点问题,利用导数判断函数性质,数形结合,即可求解.
18.(本题17分)已知抛物线过点,直线l与该抛物线C相交于M,N两点,过点M作x轴的垂线,与直线交于点G,点M关于点G的对称点为P,且O,N,P三点共线.
(1)求抛物线C的方程;
(2)若过点作,垂足为H(不与点Q重合),是否存在定点T,使得为定值?若存在,求出该定点和该定值;若不存在,请说明理由.
【答案】(1);(2)存在定点,使得为定值,该定值为
【分析】(1)将点代入抛物线方程可求出,从而可求出抛物线方程;
(2)设点,,然后表示出点的坐标,由O,N,P三点共线,化简可得,设直线l的方程为,代入抛物线方程化简,利用根与系数的关系可得,则直线l过定点,从而可得点H的轨迹是以为直径的圆.
【详解】(1)因为抛物线过点,所以,所以,
所以抛物线C的方程为.
(2)设点,,联立,得,
又因为点M关于点G的对称点为P,所以点,
由O,N,P三点共线,可得,即,
化简得,
设直线l的方程为,联立,消去x,得,
则,即,可得,,
代入,可得,可得,
所以直线l的方程:,即,则,
所以直线l过定点,
因为,
所以点H的轨迹是以为直径的圆(除去E,Q两点),圆心为,半径为,
所以存在定点,使得为定值,该定值为.
.
【点睛】关键点睛:此题考查直线与抛物线的位置关系,考查抛物线中的定点问题,解题的关键是将直线方程代入抛物线方程化简,利用根与系数的关系,再结合O,N,P三点共线的条件表示出直线方程,从而可求得直线过的定点.
19.(本题17分)对于一个有穷单调递增正整数数列P,设其各项为,,,,若数列P中存在不同的四项,,,满足,则称P为等和数列,集合称为P的一个等和子集,否则称P为不等和数列.
(1)判断下列数列是否是等和数列,若是等和数列,直接写出它的所有等和子集;A:1,3,5,7,9;B:2,4,6,7,10;
(2)已知数列P:,,,,是等和数列,并且对于任意的,总存在P的一个等和子集M满足集合,求证:数列P是等差数列;
(3)若数列P:,,,是不等和数列,求证:.
【答案】(1)是等和数列,所有的等和子集为,,;不是等和数列;(2)见解析;(3)见解析
【分析】(1)由等和数列的定义判断即可;
(2)数列P最多有如下五个等和子集:,,,,,根据反证法结合等差数列的定义证明即可;
(3)假设,且不是整数,利用反证法证明即可.
【详解】(1)A是等和数列,所有的等和子集为,,;
B是不等和数列.
(2)数列P最多有如下五个等和子集:,,,,,
考虑,,只可能是如下三种情况的一种:
,,,
若,则,不是P的等和子集,
否则,或,并且不是P的等和子集,否则,,
所以,P的所有等和子集有,,
此时,不满足,该情况不成立,即;
由对称性可知,,
因此,,此时,,不是P的等和子集,
考虑,,
故,是P的等和子集,
故,,
由以上三式可知,即数列P是等差数列.
(3)假设,且不是整数,
则对于任意,总有,
因为数列P是不等和数列,所以,至少有个不同的取值,
若存在,则,,
当时,若,则,则存在等和数列,与题设矛盾,
故时,有,
所以,,只有个不同的取值,
因此,,,
又因为存在,所以,,此时,,矛盾.
若不存在,则,恰个不同的取值,
所以,,,并且,,
此时,,矛盾.
综上,.
【点睛】思路点睛:本题考查了数列新定义问题,按着某种规律新生出另一个数列的题目,涉及到归纳推理的思想方法,对学生的思维能力要求较高,综合性强,能很好的考查学生的综合素养,解答的关键是要理解新定义,根据定义进行逻辑推理,进而解决问题.
同课章节目录
