平行四边形性质练习
图片预览




文档简介
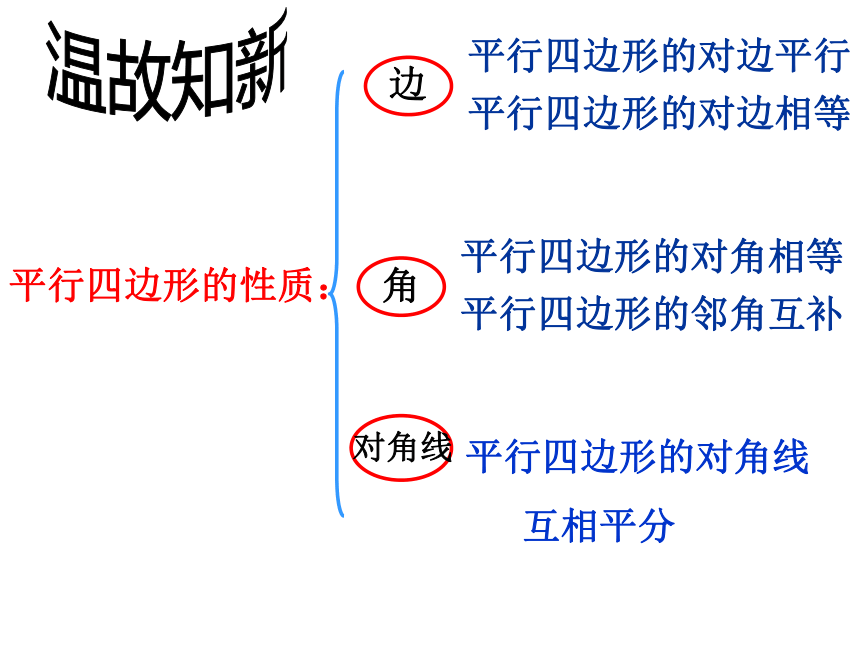
课件18张PPT。平行四边形性质训练平行四边形的性质:边平行四边形的对边平行平行四边形的对边相等角平行四边形的对角相等平行四边形的邻角互补对角线 平行四边形的对角线
互相平分 温故知新选择题:
1、 ABCD中,∠A比∠B大20°则∠C的度数为
( )
A、60 ° B、80 ° C、100° D、120°
2、 ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为 ( )
A、5cm B、 15cm C、 6cm D、 16cm
3、 ABCD中, ∠ A=43 ° ,过点A作BC和CD的垂线,那么这两条垂线的夹角度数为 ( )
A、113° B、115 ° C、137° D、90°CAC
4、 ABCD中,∠A:∠B: ∠C : ∠D的值可能是 ( )
A、1:2:3:4 B、1:2:2:1 C、2:2:1:1 D、2:1:2:1
5、 ABCD的周长为32cm,AB:BC=3:5,则CD,AD的长分别为 ( )
A、12cm,20cm B、 20cm,12cm C、 10cm,6cm D、 6cm,10cm
6、 平行四边形不具有的性质是( )
A、对边平行 B、对角相等 C、对角线相等 D、对角线平分
7、以不在同一直线上的三个点为顶点作平行四边形,最多能作
( )
A、1个 B、2个 C、3个 D、4个DDCC填空:
1、已知 ABCD的对角线相交于点O,它的周长为10cm, ⊿ BOC的周长比⊿ AOB的周长多2cm,则AB=( )
2、在 ABCD中, ∠ A的余角与∠ B的补角相等,则∠ D的度数为( )
3、已知P为 ABCD内一点, S ABCD =20,则S⊿PAB+S⊿PCD =
( )
4、若 ABCD中, ∠ BAD的平分线交BC于E,且AE=BE,则∠ BCD的度数为( )
5、已知 ABCD的周长是30cm,AB:BC=2:3,那么AB=( ) cm
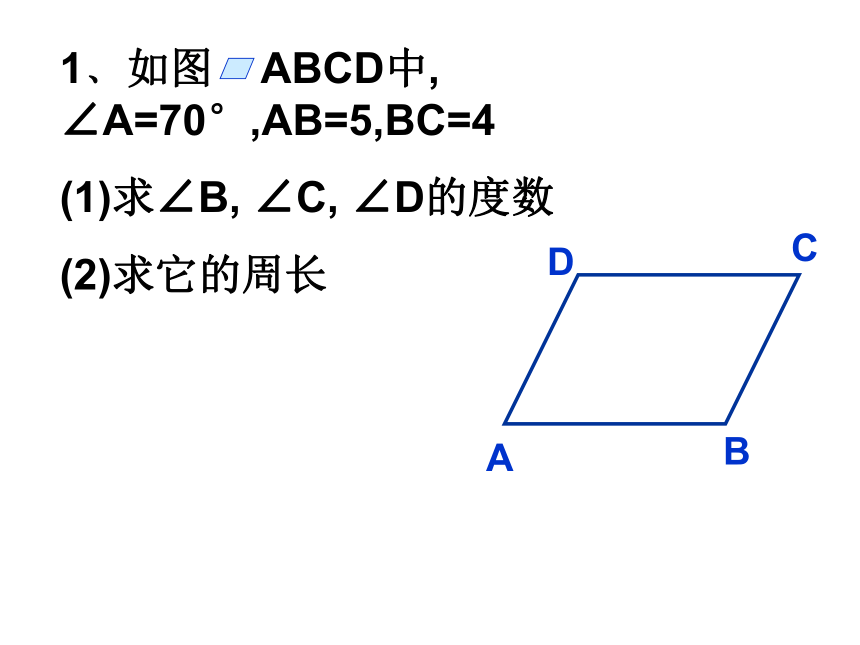
6、已知 ABCD中, ∠ B +∠ D=140°,则∠ A=( )1﹑如图 ABCD中, ∠A=70°,AB=5,BC=4
(1)求∠B, ∠C, ∠D的度数
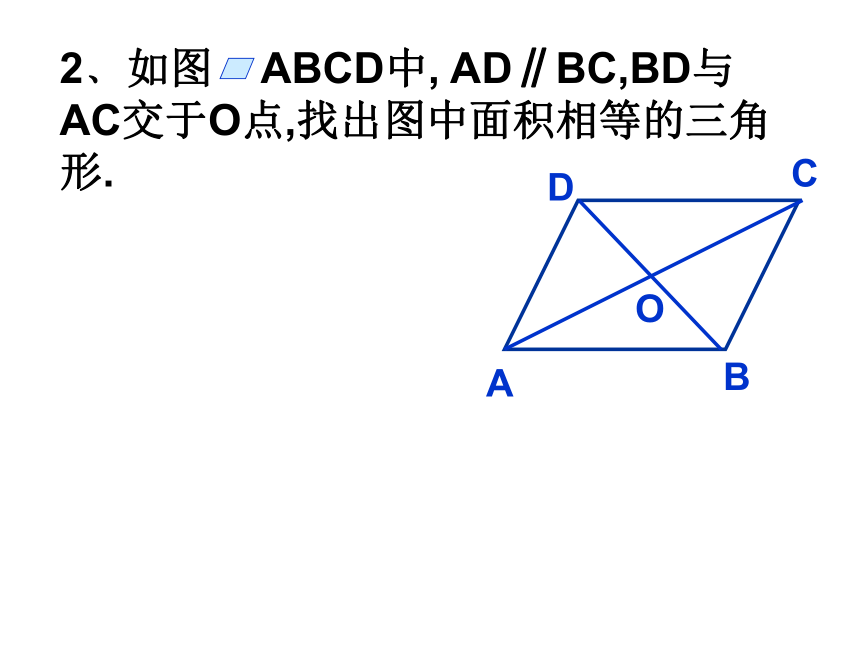
(2)求它的周长2﹑如图 ABCD中, AD∥BC,BD与AC交于O点,找出图中面积相等的三角形.3﹑ ABCD中, ∠ A的平分线分BC成4cm和3cm两条线段,求 ABCD的周长.4﹑ ABCD中, AB:BC=2:3,CD=18,
求 ABCD的周长.5﹑如图, ABCD的对角线AC,BD相交于点O, OE⊥AD于E, OF⊥BC于F,
求证:OE=OFDCBAOEF12346﹑如图, △ABC中,AB=AC,点P是BC上任一点,PE ∥ AC,PF ∥AB,分别交AB,AC于E,F,试问线段PE,PF与AB之间有什么关系,并说明理由.PCBAEF7﹑如图, △ABC中,BD平分∠ ABC,
DE ∥ BC,EF ∥AC,D,E,F分别在AC,AB,BC上,你认为BE与FC相等吗.若是,试说明理由.DCBAEF8﹑如图, 在 ABCD中,AQ,BN,CN,DQ分别是∠DAB,∠ABC,∠ BCD,∠CDA的平分线,AQ与BN,相交于P,CN与DQ交于M,在不添加其他条件的情况下,试写出一个由上述条件推出来的结论,并给出证明过程(要求推理过程中要用到”平行四边形”和”角平分线”这两个条件)DCBAQFNMP1﹑已知:如下图 ABCD中,平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N,交BA﹑BC于点PQ,求证:MQ=NPMADBNQCP证明:∵四边形ABCD是平行四边形
∴AD∥BC,AB ∥ CD
即AM ∥ CQ.
又AC ∥ MN,即AC ∥ MQ
∴四边形MQCA是平行四边形
∴ MQ=AC
同理可证:NP=AC
∴MQ=NP2、已知 ABCD中,AE⊥BD, CF⊥BD,垂足为E、F,
求证:EB=DFABCDEF证明:∵AE⊥BD,CF ⊥ BD
∴∠AEB=90°,∠CFD=90°
∴∠ AEB=∠CFD
又四边形ABCD是平行四边形
∴ AB=CD,∠ABE=∠CDF
∴ ⊿ABE≌⊿CDF
∴ BE=DF3、 ABCD中,∠A=150°,AB=8cm,BC=10cm,
求:四边形ABCD的面积ABCDE解:过点A作AE ⊥ BC交BC于E。
∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠BAD+∠B=180°
∵ ∠BAD=150 °
∴∠B=30 °
在Rt⊿ABE中,∠B=30 °
∴AE= AB=4, ∴ S ABCD=4×10=40(cm)4、已知如下图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证:BE=DF证明:
∵BE∥DF
∴∠BEO=∠DFO( )
∵四边形ABCD是平行四边形
∴OB=OD ( )
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF ( )
∴BE=DF ( )5、如图:在 ABCD中,O是对角线AC和BD的交点,OE⊥AD于E,OF⊥BC于F。
求证:OE=OF证明: ∵ OE⊥AD, OF⊥BC,
∴∠AEO=∠CFO=90 °
∵ 四边形ABCD为平行四边形
∴OA=OC( )
AD ∥ BC
∴∠ DAC=∠ACB,
∴ ⊿ AEO ≌⊿ CFO(AAS)
∴ OE=OF6、如图,四边形ABCD是平行四边形,AB边的垂直平分线经过点D,若 ABCD的周长是52cm,⊿ABD的周长比 ABCD的周长少10cm,求AB和AD的长。ABCDE7、如图:在 ABCD中,E,F分别是 AB、CD上的点,且AE=CF,
求证:DE=BFABCDEF
互相平分 温故知新选择题:
1、 ABCD中,∠A比∠B大20°则∠C的度数为
( )
A、60 ° B、80 ° C、100° D、120°
2、 ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为 ( )
A、5cm B、 15cm C、 6cm D、 16cm
3、 ABCD中, ∠ A=43 ° ,过点A作BC和CD的垂线,那么这两条垂线的夹角度数为 ( )
A、113° B、115 ° C、137° D、90°CAC
4、 ABCD中,∠A:∠B: ∠C : ∠D的值可能是 ( )
A、1:2:3:4 B、1:2:2:1 C、2:2:1:1 D、2:1:2:1
5、 ABCD的周长为32cm,AB:BC=3:5,则CD,AD的长分别为 ( )
A、12cm,20cm B、 20cm,12cm C、 10cm,6cm D、 6cm,10cm
6、 平行四边形不具有的性质是( )
A、对边平行 B、对角相等 C、对角线相等 D、对角线平分
7、以不在同一直线上的三个点为顶点作平行四边形,最多能作
( )
A、1个 B、2个 C、3个 D、4个DDCC填空:
1、已知 ABCD的对角线相交于点O,它的周长为10cm, ⊿ BOC的周长比⊿ AOB的周长多2cm,则AB=( )
2、在 ABCD中, ∠ A的余角与∠ B的补角相等,则∠ D的度数为( )
3、已知P为 ABCD内一点, S ABCD =20,则S⊿PAB+S⊿PCD =
( )
4、若 ABCD中, ∠ BAD的平分线交BC于E,且AE=BE,则∠ BCD的度数为( )
5、已知 ABCD的周长是30cm,AB:BC=2:3,那么AB=( ) cm
6、已知 ABCD中, ∠ B +∠ D=140°,则∠ A=( )1﹑如图 ABCD中, ∠A=70°,AB=5,BC=4
(1)求∠B, ∠C, ∠D的度数
(2)求它的周长2﹑如图 ABCD中, AD∥BC,BD与AC交于O点,找出图中面积相等的三角形.3﹑ ABCD中, ∠ A的平分线分BC成4cm和3cm两条线段,求 ABCD的周长.4﹑ ABCD中, AB:BC=2:3,CD=18,
求 ABCD的周长.5﹑如图, ABCD的对角线AC,BD相交于点O, OE⊥AD于E, OF⊥BC于F,
求证:OE=OFDCBAOEF12346﹑如图, △ABC中,AB=AC,点P是BC上任一点,PE ∥ AC,PF ∥AB,分别交AB,AC于E,F,试问线段PE,PF与AB之间有什么关系,并说明理由.PCBAEF7﹑如图, △ABC中,BD平分∠ ABC,
DE ∥ BC,EF ∥AC,D,E,F分别在AC,AB,BC上,你认为BE与FC相等吗.若是,试说明理由.DCBAEF8﹑如图, 在 ABCD中,AQ,BN,CN,DQ分别是∠DAB,∠ABC,∠ BCD,∠CDA的平分线,AQ与BN,相交于P,CN与DQ交于M,在不添加其他条件的情况下,试写出一个由上述条件推出来的结论,并给出证明过程(要求推理过程中要用到”平行四边形”和”角平分线”这两个条件)DCBAQFNMP1﹑已知:如下图 ABCD中,平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N,交BA﹑BC于点PQ,求证:MQ=NPMADBNQCP证明:∵四边形ABCD是平行四边形
∴AD∥BC,AB ∥ CD
即AM ∥ CQ.
又AC ∥ MN,即AC ∥ MQ
∴四边形MQCA是平行四边形
∴ MQ=AC
同理可证:NP=AC
∴MQ=NP2、已知 ABCD中,AE⊥BD, CF⊥BD,垂足为E、F,
求证:EB=DFABCDEF证明:∵AE⊥BD,CF ⊥ BD
∴∠AEB=90°,∠CFD=90°
∴∠ AEB=∠CFD
又四边形ABCD是平行四边形
∴ AB=CD,∠ABE=∠CDF
∴ ⊿ABE≌⊿CDF
∴ BE=DF3、 ABCD中,∠A=150°,AB=8cm,BC=10cm,
求:四边形ABCD的面积ABCDE解:过点A作AE ⊥ BC交BC于E。
∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠BAD+∠B=180°
∵ ∠BAD=150 °
∴∠B=30 °
在Rt⊿ABE中,∠B=30 °
∴AE= AB=4, ∴ S ABCD=4×10=40(cm)4、已知如下图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证:BE=DF证明:
∵BE∥DF
∴∠BEO=∠DFO( )
∵四边形ABCD是平行四边形
∴OB=OD ( )
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF ( )
∴BE=DF ( )5、如图:在 ABCD中,O是对角线AC和BD的交点,OE⊥AD于E,OF⊥BC于F。
求证:OE=OF证明: ∵ OE⊥AD, OF⊥BC,
∴∠AEO=∠CFO=90 °
∵ 四边形ABCD为平行四边形
∴OA=OC( )
AD ∥ BC
∴∠ DAC=∠ACB,
∴ ⊿ AEO ≌⊿ CFO(AAS)
∴ OE=OF6、如图,四边形ABCD是平行四边形,AB边的垂直平分线经过点D,若 ABCD的周长是52cm,⊿ABD的周长比 ABCD的周长少10cm,求AB和AD的长。ABCDE7、如图:在 ABCD中,E,F分别是 AB、CD上的点,且AE=CF,
求证:DE=BFABCDEF
