湖南省桃江县第一中学2015-2016学年高一上学期入学考试数学试题
文档属性
| 名称 | 湖南省桃江县第一中学2015-2016学年高一上学期入学考试数学试题 | 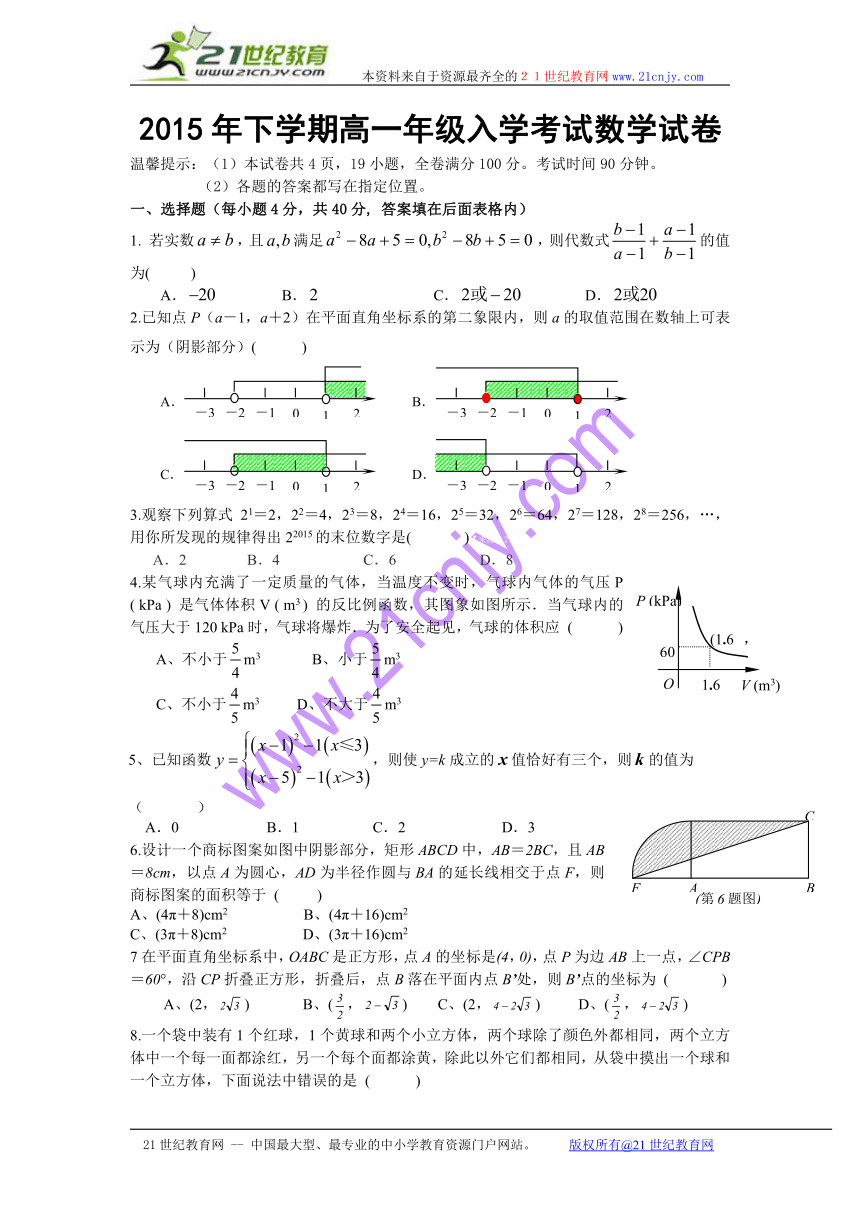 | |
| 格式 | zip | ||
| 文件大小 | 581.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-29 20:01:02 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2015年下学期高一年级入学考试数学试卷
温馨提示:(1)本试卷共4页,19小题,全卷满分100分。考试时间90分钟。
(2)各题的答案都写在指定位置。
一、选择题(每小题4分,共40分, 答案填在后面表格内)
1. 若实数,且满足,则代数式的值为( )
A. B. C. D.
2.已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为(阴影部分)( )21cnjy.com
( http: / / www.21cnjy.com )
3.观察下列算式 21=2,22=4,2 ( http: / / www.21cnjy.com )3=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律得出22015的末位数字是( )【来源:21·世纪·教育·网】
A.2 B.4 C.6 D.8
4.某气球内充满了一定质量的气体,当温度不 ( http: / / www.21cnjy.com )变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应 ( )
A、不小于m3 B、小于m3
C、不小于m3 D、不大于m3
5、已知函数,则使y=k成立的值恰好有三个,则的值为( )
A.0 B.1 C.2 D.3
6.设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于 ( )21·世纪*教育网
A、(4π+8)cm2 B、(4π+16)cm2
C、(3π+8)cm2 D、(3π+16)cm2
7在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则B’点的坐标为 ( )
A、(2,) B、(,) C、(2,) D、(,)
8.一个袋中装有1个红球,1个黄球和两个小立方体,两个球除了颜色外都相同,两个立方体中一个每一面都涂红,另一个每个面都涂黄,除此以外它们都相同,从袋中摸出一个球和一个立方体,下面说法中错误的是 ( )www-2-1-cnjy-com
A、所有可能出现的结果有四种
B、摸出2个都是红的概率为1/4
C、摸出2个都是黄的概率为1/4
D、摸出一红一黄的概率也是1/4
9.如图所示,二次函数的图象经过点,且与轴交点的横坐标分别为,其中,,下列结论: ①; ②; ③;
④.其中正确的有 ( )
A、1个 B、2个 C、3个 D、4个
10.如图,AB是⊙O的弦,C是AB的三等分点,连结OC并延长交⊙O于点D。
若OC=3,CD=2,则圆心O到弦AB的距离是( )
A.6 B.9- C. D.25-3
二、填空题(每小题4分,共20分, 答案填在后面指定位置。)
11.若代数式可化为,则的值是 .
12.比较大小:- -(“>”,或“<”).
13.计算:=________________________
14.汶川地震后需搭建简易帐篷,搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②、图③的方式串起来搭建,则串7顶这样的帐篷需要 根钢管。
[21世纪教育网]
15.已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1 、x2,则 (x1-1)2+(x2-1)2的最小值是 。2-1-c-n-j-y
题次 1 2 3 4 5 6 7 8 9 10
答案
一. 选择题(本大题共10小题,每小题4分,共40分)
二. 填空题(本大题共5小题,每小题4分,共20分)
11、 12、 ( http: / / www.21cnjy.com ) 13、 14、 15、 21世纪教育网 21*cnjy*com
三、解答题(共40分, 每题10分)
16.化简再求值: ,其中,。
17.已知二次函数,其中(1)若方程有两个实根,且方程有两个相等的根,求的解析式; (2)若的图象与x轴交于A(-3,0) B(m,0)两点, 且当时, 恒成立.求实数的取值范围.www.21-cn-jy.com
18.已知R为全集, (1)求A , B ,,;
(2) 求.
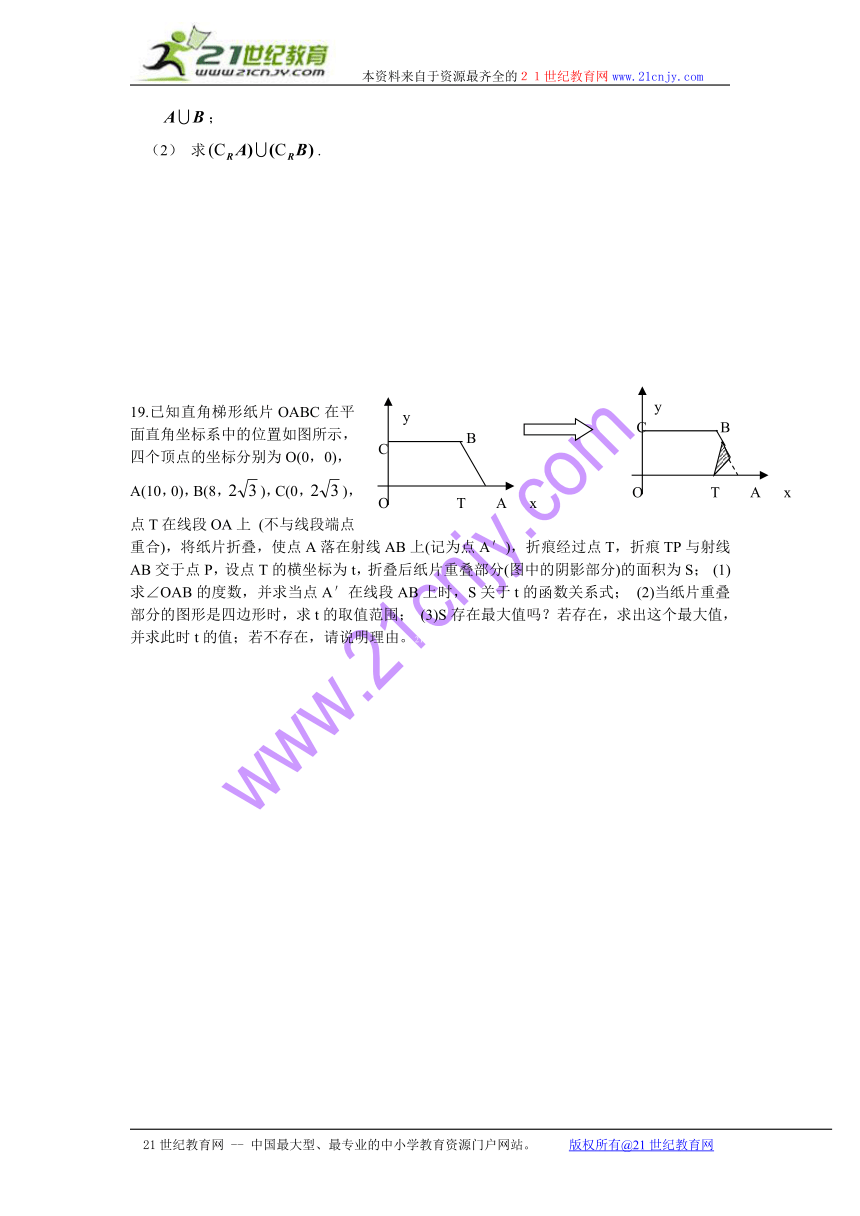
19.已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),
A(10,0),B(8,),C(0,),点T在线段OA上 (不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S; (1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式; (2)当纸片重叠部分的图形是四边形时,求t的取值范围; (3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由。21教育网
一. 选择题(本大题共10小题,每小题4分,共40分)
题次 1 2 3 4 5 6 7 8 9 10
答案 A C C C D B C D D C
二. 填空题(本大题共5小题,每小题5分,共25分)
11、 5 12、 < 13、 9 14、 83 15、 8
三、解答题
17. 解:(1)A=[-1,3),B=[2,3] ,,
(2)=={x︳x<2或x≥3}
18. 解:(1)据题意,设
①
由方程 ②
因为方程②有两个相等的根,所以, [来源:21世纪教育网]
即 (舍去)
将代入①得的解析式
(2) 据题意知,是方程的两个根.由韦达定理
故方程可化为
要使得当时,恒成立.当且仅当 ( http: / / www.21cnjy.com )
故实数的取值范围为
19. 解:(1) ∵A,B两点的坐标分别是A(10,0)和B(一. 选择题(本大题共10小题,每小题4分,共40分)21·cn·jy·com
题次 1 2 3 4 5 6 7 8 9 10
答案 A C C C D B C D D C
二. 填空题(本大题共5小题,每小题5分,共25分)
11、 5 12、 < 13、 9 14、 83 15、 8
三、解答题
( http: / / www.21cnjy.com )
17. 解:(1)A=[-1,3),B=[2,3] ,,
(2)=={x︳x<2或x≥3}
18. 解:(1)据题意,设
①
由方程 ②
因为方程②有两个相等的根,所以,
即 (舍去)
将代入①得的解析式
(2) 据题意知,是方程的两个根.由韦达定理
故方程可化为
要使得当时,恒成立.当且仅当 ( http: / / www.21cnjy.com )
故实数的取值范围为
19. 解:(1) ∵A,B两点的坐标分别是A(10,0)和B(8,),
∴, ∴
当点A 在线段AB上时,∵,TA=TA ,
∴△A TA是等边三角形,且,
∴,,
纸片重叠部分的图形是四边形(如图(1),其中E是TA 与CB的交点),21世纪教育网
当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
又由(1)中求得当A 与B重合时,T的坐标是(6,0)
所以当纸片重叠部分的图形是四边形时,。
(3)S存在最大值
当时,,
在对称轴t=10的左边,S的值随着t的增大而减小,
∴当t=6时,S的值最大是。
当时,由图,重叠部分的面积
∵△A EB的高是,
∴
当t=2时,S的值最大是;
当,即当点A 和点P都在线段AB的延长线是(如图,其中E是TA 与CB的交点,F是TP与CB的交点),21世纪教育网21世纪教育网版权所有
∵,四边形ETAB是等腰形,∴EF=ET=AB=4,
∴
综上所述,S的最大值是,此时t的值是。
8,),
∴, ∴
当点A 在线段AB上时,∵,TA=TA ,
∴△A TA是等边三角形,且,
∴,,
纸片重叠部分的图形是四边形(如图(1),其中E是TA 与CB的交点),
当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
又由(1)中求得当A 与B重合时,T的坐标是(6,0)
所以当纸片重叠部分的图形是四边形时,。
(3)S存在最大值
当时,,
在对称轴t=10的左边,S的值随着t的增大而减小,
∴当t=6时,S的值最大是。
当时,由图,重叠部分的面积
∵△A EB的高是,
∴
当t=2时,S的值最大是;
当,即当点A 和点P都在线段AB的延长线是(如图,其中E是TA 与CB的交点,F是TP与CB的交点),2·1·c·n·j·y
∵,四边形ETAB是等腰形,∴EF=ET=AB=4,
∴
综上所述,S的最大值是,此时t的值是。
1
-2
-3
-1
0
2
A.
1
-2
-3
-1
0
2
B.
C.
1
-2
-3
-1
0
2
D.
1
-2
-3
-1
0
2
1.6
60
O
V (m3)
P (kPa)
(1.6,60)
A
B
C
F
(第6题图)
第9题图
1
-1
-2
2
x
y
O
图① 图② 图③
B
B
y
y
O
C
O
C
T A x
T A x
A
y
x
P
B
E
F
C
A
T
O
A
y
x
P
B
E
F
C
A
T
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2015年下学期高一年级入学考试数学试卷
温馨提示:(1)本试卷共4页,19小题,全卷满分100分。考试时间90分钟。
(2)各题的答案都写在指定位置。
一、选择题(每小题4分,共40分, 答案填在后面表格内)
1. 若实数,且满足,则代数式的值为( )
A. B. C. D.
2.已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为(阴影部分)( )21cnjy.com
( http: / / www.21cnjy.com )
3.观察下列算式 21=2,22=4,2 ( http: / / www.21cnjy.com )3=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律得出22015的末位数字是( )【来源:21·世纪·教育·网】
A.2 B.4 C.6 D.8
4.某气球内充满了一定质量的气体,当温度不 ( http: / / www.21cnjy.com )变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应 ( )
A、不小于m3 B、小于m3
C、不小于m3 D、不大于m3
5、已知函数,则使y=k成立的值恰好有三个,则的值为( )
A.0 B.1 C.2 D.3
6.设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于 ( )21·世纪*教育网
A、(4π+8)cm2 B、(4π+16)cm2
C、(3π+8)cm2 D、(3π+16)cm2
7在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则B’点的坐标为 ( )
A、(2,) B、(,) C、(2,) D、(,)
8.一个袋中装有1个红球,1个黄球和两个小立方体,两个球除了颜色外都相同,两个立方体中一个每一面都涂红,另一个每个面都涂黄,除此以外它们都相同,从袋中摸出一个球和一个立方体,下面说法中错误的是 ( )www-2-1-cnjy-com
A、所有可能出现的结果有四种
B、摸出2个都是红的概率为1/4
C、摸出2个都是黄的概率为1/4
D、摸出一红一黄的概率也是1/4
9.如图所示,二次函数的图象经过点,且与轴交点的横坐标分别为,其中,,下列结论: ①; ②; ③;
④.其中正确的有 ( )
A、1个 B、2个 C、3个 D、4个
10.如图,AB是⊙O的弦,C是AB的三等分点,连结OC并延长交⊙O于点D。
若OC=3,CD=2,则圆心O到弦AB的距离是( )
A.6 B.9- C. D.25-3
二、填空题(每小题4分,共20分, 答案填在后面指定位置。)
11.若代数式可化为,则的值是 .
12.比较大小:- -(“>”,或“<”).
13.计算:=________________________
14.汶川地震后需搭建简易帐篷,搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②、图③的方式串起来搭建,则串7顶这样的帐篷需要 根钢管。
[21世纪教育网]
15.已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1 、x2,则 (x1-1)2+(x2-1)2的最小值是 。2-1-c-n-j-y
题次 1 2 3 4 5 6 7 8 9 10
答案
一. 选择题(本大题共10小题,每小题4分,共40分)
二. 填空题(本大题共5小题,每小题4分,共20分)
11、 12、 ( http: / / www.21cnjy.com ) 13、 14、 15、 21世纪教育网 21*cnjy*com
三、解答题(共40分, 每题10分)
16.化简再求值: ,其中,。
17.已知二次函数,其中(1)若方程有两个实根,且方程有两个相等的根,求的解析式; (2)若的图象与x轴交于A(-3,0) B(m,0)两点, 且当时, 恒成立.求实数的取值范围.www.21-cn-jy.com
18.已知R为全集, (1)求A , B ,,;
(2) 求.
19.已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),
A(10,0),B(8,),C(0,),点T在线段OA上 (不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S; (1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式; (2)当纸片重叠部分的图形是四边形时,求t的取值范围; (3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由。21教育网
一. 选择题(本大题共10小题,每小题4分,共40分)
题次 1 2 3 4 5 6 7 8 9 10
答案 A C C C D B C D D C
二. 填空题(本大题共5小题,每小题5分,共25分)
11、 5 12、 < 13、 9 14、 83 15、 8
三、解答题
17. 解:(1)A=[-1,3),B=[2,3] ,,
(2)=={x︳x<2或x≥3}
18. 解:(1)据题意,设
①
由方程 ②
因为方程②有两个相等的根,所以, [来源:21世纪教育网]
即 (舍去)
将代入①得的解析式
(2) 据题意知,是方程的两个根.由韦达定理
故方程可化为
要使得当时,恒成立.当且仅当 ( http: / / www.21cnjy.com )
故实数的取值范围为
19. 解:(1) ∵A,B两点的坐标分别是A(10,0)和B(一. 选择题(本大题共10小题,每小题4分,共40分)21·cn·jy·com
题次 1 2 3 4 5 6 7 8 9 10
答案 A C C C D B C D D C
二. 填空题(本大题共5小题,每小题5分,共25分)
11、 5 12、 < 13、 9 14、 83 15、 8
三、解答题
( http: / / www.21cnjy.com )
17. 解:(1)A=[-1,3),B=[2,3] ,,
(2)=={x︳x<2或x≥3}
18. 解:(1)据题意,设
①
由方程 ②
因为方程②有两个相等的根,所以,
即 (舍去)
将代入①得的解析式
(2) 据题意知,是方程的两个根.由韦达定理
故方程可化为
要使得当时,恒成立.当且仅当 ( http: / / www.21cnjy.com )
故实数的取值范围为
19. 解:(1) ∵A,B两点的坐标分别是A(10,0)和B(8,),
∴, ∴
当点A 在线段AB上时,∵,TA=TA ,
∴△A TA是等边三角形,且,
∴,,
纸片重叠部分的图形是四边形(如图(1),其中E是TA 与CB的交点),21世纪教育网
当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
又由(1)中求得当A 与B重合时,T的坐标是(6,0)
所以当纸片重叠部分的图形是四边形时,。
(3)S存在最大值
当时,,
在对称轴t=10的左边,S的值随着t的增大而减小,
∴当t=6时,S的值最大是。
当时,由图,重叠部分的面积
∵△A EB的高是,
∴
当t=2时,S的值最大是;
当,即当点A 和点P都在线段AB的延长线是(如图,其中E是TA 与CB的交点,F是TP与CB的交点),21世纪教育网21世纪教育网版权所有
∵,四边形ETAB是等腰形,∴EF=ET=AB=4,
∴
综上所述,S的最大值是,此时t的值是。
8,),
∴, ∴
当点A 在线段AB上时,∵,TA=TA ,
∴△A TA是等边三角形,且,
∴,,
纸片重叠部分的图形是四边形(如图(1),其中E是TA 与CB的交点),
当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
又由(1)中求得当A 与B重合时,T的坐标是(6,0)
所以当纸片重叠部分的图形是四边形时,。
(3)S存在最大值
当时,,
在对称轴t=10的左边,S的值随着t的增大而减小,
∴当t=6时,S的值最大是。
当时,由图,重叠部分的面积
∵△A EB的高是,
∴
当t=2时,S的值最大是;
当,即当点A 和点P都在线段AB的延长线是(如图,其中E是TA 与CB的交点,F是TP与CB的交点),2·1·c·n·j·y
∵,四边形ETAB是等腰形,∴EF=ET=AB=4,
∴
综上所述,S的最大值是,此时t的值是。
1
-2
-3
-1
0
2
A.
1
-2
-3
-1
0
2
B.
C.
1
-2
-3
-1
0
2
D.
1
-2
-3
-1
0
2
1.6
60
O
V (m3)
P (kPa)
(1.6,60)
A
B
C
F
(第6题图)
第9题图
1
-1
-2
2
x
y
O
图① 图② 图③
B
B
y
y
O
C
O
C
T A x
T A x
A
y
x
P
B
E
F
C
A
T
O
A
y
x
P
B
E
F
C
A
T
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
