数学(北师大版)必修五教学设计:2.3 解三角形的实际应用举例
文档属性
| 名称 | 数学(北师大版)必修五教学设计:2.3 解三角形的实际应用举例 |

|
|
| 格式 | zip | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-30 10:43:01 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
教学设计
3 解三角形的实际应用举例
教学分析
本节重点研究底部不可到达的高度测量问题, ( http: / / www.21cnjy.com )这类问题在我们的日常生活中比比皆是,学生对实际背景非常熟悉,这给教学带来了极大的便利.由于底部不可到达,这类问题不能直接用解直角三角形的方法来解决,但用正弦定理和余弦定理就可以计算出建筑物顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.教学时要充分利用多媒体课件给学生以动态演示,加强直观感知.
本节课主要是测量问题,一是要熟悉仰角、俯角的意义,二是要会在几个三角形中找出已知量与未知量之间的关系,逐步转化,最终归结为解三角形的问题.
三维目标
1.结合实际测量工具,能用正弦定理、余弦定理等知识解决生活中一些有关底部不可到达的物体高度的测量问题.
2.使学生体会数学知识来源于生活并应用于生 ( http: / / www.21cnjy.com )活,进一步培养学生学习数学、应用数学的意识以及观察、归纳、类比、概括的能力.提高灵活地选择正弦定理、余弦定理的解题能力.
3.通过本节的探究,引导学生经过自己的数学 ( http: / / www.21cnjy.com )活动,从实际问题中提取数学模型,使学生经历发现和创造过程,进一步拓展学生的数学活动空间,发展学生“做数学”“用数学”的意识.
重点难点
教学重点:分析测量物体高度 ( http: / / www.21cnjy.com )问题的实际背景,正确运用正弦定理、余弦定理解决底部不可到达的测量物体高度的问题,进一步熟悉数学建模的方法步骤,熟悉解决实际问题的规范的解题过程.
教学难点:将测量底部不可到达物体的高度问题转化为数学问题是本节的难点,另一个难点是灵活选用正弦定理和余弦定理.
课时安排
2课时
第1课时
导入新课
思路1.(问题导入)现实生活中,人们又 ( http: / / www.21cnjy.com )是怎样测量底部不可到达的建筑物高度的呢?通过学习本节你将轻松愉快地测量出山高和工厂的烟囱高,在学生踊跃的状态下展开新课.或者先让学生说一说我们校园内水塔的高度测量问题,在学生纷纷寻求测量水塔高度的方法争论中自然地引入新课.
思路2.(情境导入)你有坐汽车(或 ( http: / / www.21cnjy.com )者火车)经过山前水平公路的经历吗?如果身边带着测角仪,那么根据路标(100米杆)就会立即测算出你所看到的山的高度.利用正弦定理、余弦定理你也会马上算出来,在学生急切想知道如何测算山高的期待中展开新课.
推进新课
①回忆正弦定理、余弦定理,并提出已知三角形的两边及一边的对角选用哪个定理?,
②怎样将实际问题转化为解三角形问题?
③如果底部可到达,如电线杆的高度应怎样测量?如果底部不能到达,如工厂的烟囱的高度应怎样测量呢?
④对解题中的近似值怎样处理才能减小误差呢?
活动:教师先让学生回忆正弦定理、余 ( http: / / www.21cnjy.com )弦定理的内容,学生很快回忆起来,若已知三角形的两边及其中一边的对角先用正弦定理较好.引导学生回忆数学建模的方法步骤:分析→建模→求解→检验,鼓励学生多动手画图.特别是对想象能力较弱的学生,更应画出图形,在图形上标出已知的数据以加强直观感知.21·世纪*教育网
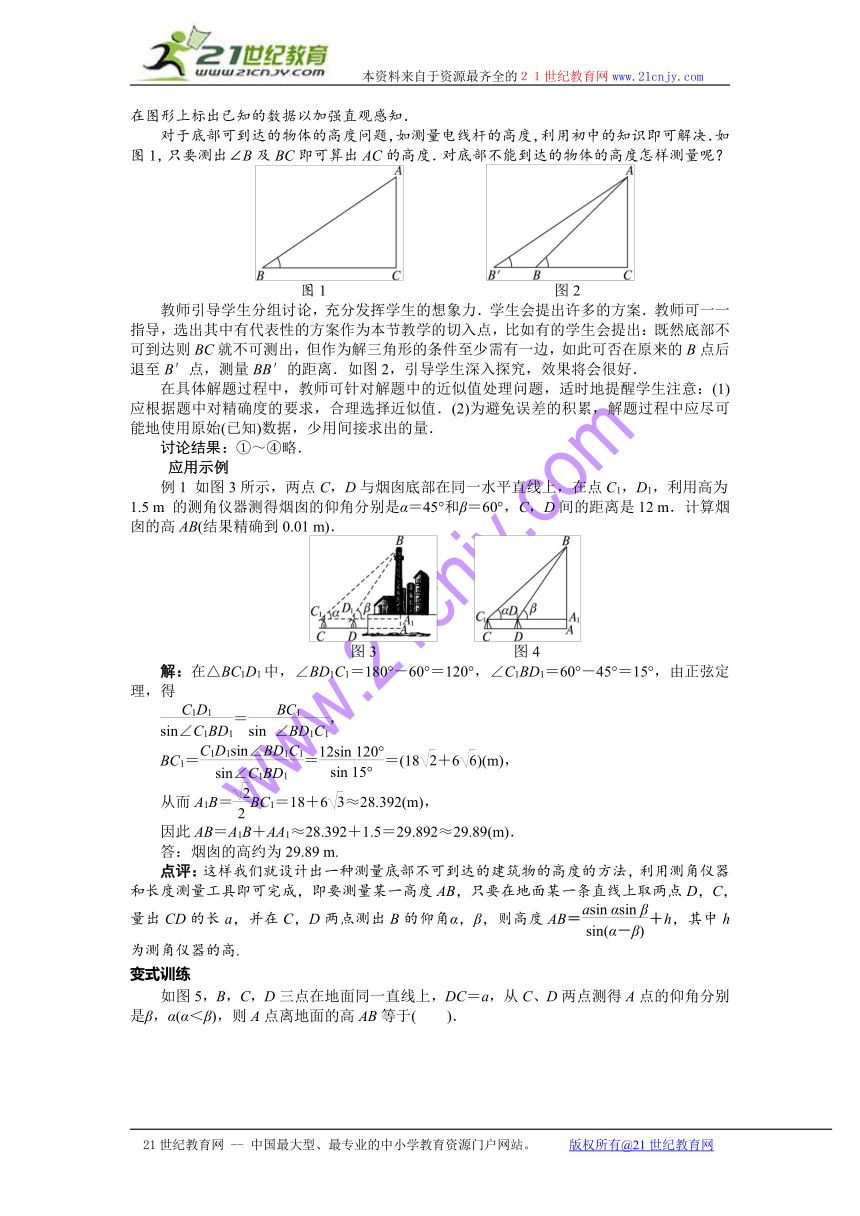
对于底部可到达的物体的高度问题,如测量电线杆 ( http: / / www.21cnjy.com )的高度,利用初中的知识即可解决.如图1,只要测出∠B及BC即可算出AC的高度.对底部不能到达的物体的高度怎样测量呢?
图1 图2[]
教师引导学生分组讨论,充分 ( http: / / www.21cnjy.com )发挥学生的想象力.学生会提出许多的方案.教师可一一指导,选出其中有代表性的方案作为本节教学的切入点,比如有的学生会提出:既然底部不可到达则BC就不可测出,但作为解三角形的条件至少需有一边,如此可否在原来的B点后退至B′点,测量BB′的距离.如图2,引导学生深入探究,效果将会很好.
在具体解题过程中,教师可 ( http: / / www.21cnjy.com )针对解题中的近似值处理问题,适时地提醒学生注意:(1)应根据题中对精确度的要求,合理选择近似值.(2)为避免误差的积累,解题过程中应尽可能地使用原始(已知)数据,少用间接求出的量.2-1-c-n-j-y
讨论结果:①~④略.
例1 如图3所示,两点C,D与烟囱底部 ( http: / / www.21cnjy.com )在同一水平直线上,在点C1,D1,利用高为1.5 m 的测角仪器测得烟囱的仰角分别是α=45°和β=60°,C,D间的距离是12 m.计算烟囱的高AB(结果精确到0.01 m).
图3 图4
解:在△BC1D1中,∠BD1C1=180°-60°=120°,∠C1BD1=60°-45°=15°,由正弦定理,得
=,
BC1===(18+6)(m),
从而A1B=BC1=18+6≈28.392(m),
因此AB=A1B+AA1≈28.392+1.5=29.892≈29.89(m).
答:烟囱的高约为29.89 m.
点评:这样我们就设计出一种测量底部不可 ( http: / / www.21cnjy.com )到达的建筑物的高度的方法,利用测角仪器和长度测量工具即可完成,即要测量某一高度AB,只要在地面某一条直线上取两点D,C,量出CD的长a,并在C,D两点测出B的仰角α,β,则高度AB=+h,其中h为测角仪器的高.
变式训练
如图5,B,C,D三点在地面同一直线上,DC=a,从C、D两点测得A点的仰角分别是β,α(α<β),则A点离地面的高AB等于( ).
图5
A. B. C. D.
答案:C
例2 如图6,在山顶铁塔上B处测得 ( http: / / www.21cnjy.com )地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′.已知铁塔BC部分的高为27.3 m,求出山高CD(精确到0.1 m).
图6 图7
活动:本题实际上是上例的变式训练.
教师引导学生观察图形,弄清俯角是什么意思 ( http: / / www.21cnjy.com ).假若把该图以D为支点逆时针旋转90°,如图7,让学生观察此图与例1图形的异同.教师要给学生留出一定的探究时间,让学生充分讨论思考,学生会发现,例1、例2两题图形的形状是一致的,这里易知∠ABC=90°-α,∠ACB=90°+β及BC=27.3 m,而求CD(如图7).学生只要探究到这步,以下的问题可完全由学生自己解决,教师只是点拨其解题步骤的书写及近似值的确定即可.[]
解:在△ABC中,∠BCA=90°+β,∠ABC=90°-α,∠BAC=α-β,∠BAD=α.
根据正弦定理,=,
所以AB==.
解Rt△ABD,得BD=ABsin∠BAD=.
将测量数据代入上式,得
BD==≈176.5(m),
CD=BD-BC≈176.5-27.3≈149.2(m).
答:山的高度约为149.2 m.
点评:本题学生也可能这样求解:先在△ABC中求得AC,再在Rt△ACD中直接求得CD,教师应鼓励学生这样思考很好,更直接.2·1·c·n·j·y
变式训练
有一长为10 m的斜坡,它的倾斜角是75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延伸( ).
A.5 m B.10 m
C.10 m D.10 m
解析:如图8,在△ABC中,设BC=x m,由正弦定理,可知
图8
=,
∴x=10(m).
答案:C
例3 如图9,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15°的方向上,行驶5 km后到达B处,测得此山顶在西偏北25°的方向上,仰角为8°,求此山的高度CD.(sin 15 °≈0.258 8,sin 10°≈0.173 6,tan 8°≈0.140 5)
图9
活动:教师引导学生充分理解题目背景, ( http: / / www.21cnjy.com )引导学生画出图形.首先理解什么是仰角,西偏北25°是什么意思.本题的图形是一个立体几何图形,让学生充分理解图形中的各个已知量和要求的量.
解:在△ABC中,∠CAB=15°,∠ACB=25°-15°=10°,
根据正弦定理,=,BC==≈7.453 9(km),
CD=BC×tan∠DBC≈BC×tan 8°≈1 047(m).
答:山的高度约为1 047 m.
点评:本例中三角形较多,要根据已知条件及所求的边长恰当选取我们需要的三角形.
变式训练
如图10,地平面上有一旗杆OP,为了测 ( http: / / www.21cnjy.com )得它的高度h,在地面上选一基线AB,AB=20 m,在A点处测得P点的仰角∠OAP=30°,在B点处测得P点的仰角∠OBP=45°,又测得∠AOB=60°,求旗杆的高度h(结果保留两个有效数字).
图10
活动:在看图时要注意结合实际— ( http: / / www.21cnjy.com )—旗杆OP垂直地面,所以△AOP和△BOP都是直角三角形.又这两个三角形中各已知一个锐角,那么其他各边均可用h的代数式表示.在△AOB中,已知一边及其对角,另两边均为h的代数式,可利用余弦定理构造方程,解这个方程即可求出旗杆高h.
解:在Rt△AOP中,∠OAP=30°,OP=h,
∴OA=OP·cot 30°=h.
在Rt△BOP中,∠OBP=45°,
∴OB=OP=h.
在△AOB中,AB=20,∠AOB=60°,
由余弦定理,得
AB2=OA2+OB2-2×OA×OB·cos 60°,
即202=(h)2+h2-2·h·h·.
解得h2=≈176.4,∴h≈13(m).
答:旗杆高度约为13 m.
点评:(1)仰角和俯角是在同一铅垂面内视线与水平线的夹角,当视线在水平线之上时称为仰角,当视线在水平线之下时称为俯角.21*cnjy*com
(2)由余弦定理(正弦定理)构造方程,是解决此问题的关键.方程思想是解决问题的一种常用思想方法.[]
例4自动卸货汽车采用液压机构.设计时需 ( http: / / www.21cnjy.com )要计算油泵顶杠BC的长度,如图11所示.已知车厢的最大仰角为60°(指车厢AC与水平线夹角),油泵顶点B与车厢支点A之间的距离为1.95 m,AB与水平线之间的夹角为6°20′,AC长为1.40 m.计算BC的长度(结果精确到0.01 m).
图11 图12
活动:本例是一道经典例题,教师引导学生先观察实物模型,通过阅读题意画出几何图形.
这个问题就是在△ABC(如图12)中,已知AB=1.95 m,AC=1.40 m,∠BAC=60°+6°20′=66°20′,求BC的长.
解:由余弦定理,得
BC2=AB2+AC2-2AB·ACcos A
=1.952+1.402-2×1.95×1.40cos 66°20′[]
≈3.571,
所以BC≈1.89(m).
答:顶杆BC约长1.89 m.
课本本节练习1,2.
先由学生自己回顾本节所学的测量底部不可到达 ( http: / / www.21cnjy.com )的建筑物高度的方法,是如何从实际问题情境中寻求到解决问题的方案的?你是否能根据题意准确地画出示意图?你没有画出的原因是什么?
在学生自己总结归纳,对本节有 ( http: / / www.21cnjy.com )了一个整体认识的时候,教师可作进一步的归纳.解决实际问题的关键是建立数学模型,特别是画出示意图是准确迅速解这个数学问题的关键,也是本节要体现的技能,这在高考中体现得很突出,需要在反复的练习和动手操作中提高这方面的能力.
课本习题2-3 A组4.
本教案设计以情境教学、问题教学为主,教 ( http: / / www.21cnjy.com )师引导和学生积极参与探究相结合,充分体现以学为主、逐步领悟的原则.日常生活中的实例体现了数学知识的生动运用.通过合作学习和相互提问补充的方法让学生多感受问题的演变过程,通过多媒体课件的演示让学生切身感受实际问题所反映的数学本质,让学生在轻松愉快的互动气氛中学到知识,提高能力.
本教案设计的中心主线是在学生探究活动中 ( http: / / www.21cnjy.com )提炼数学建模,不要求学生死记硬背解决实际问题的方法步骤.本教案的设计始终抓住本节乃至本章的这一重点,不在一些细枝末节上浪费时间.
通过本节及上节的探究,学生基本上熟悉了解决实际问题的思想方法,下一步教师要在规范步骤等方面加以关注.
备用习题
1.在一幢20m高的楼顶测得对面一塔顶的仰角为60°,塔基的俯角为45°,则塔高为( ).
A.20(1+) m B.20(1+) m
C.10(+) m D.20(+) m
2.在某时刻,A点西400 km的B处是 ( http: / / www.21cnjy.com )台风中心,台风以每小时40 km的速度向东北方向直线前进,以台风中心为圆心、300 km为半径的圆称为“台风圈”,从此时刻算起,大约经过多长时间A进入台风圈?A处在台风圈中的时间有多长(结果保留根号)
3.如图13,我炮兵阵地位于地面A处,两观察 ( http: / / www.21cnjy.com )所分别位于地面点C和D处,已知CD=6 000 m,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°,求炮兵阵地到目标的距离(结果保留根号).
图13 图14
4.如图14,测量人员沿直线MNP的 ( http: / / www.21cnjy.com )方向测量,测得A点的仰角分别是∠AMB=30°,∠ANB=45°,∠APB=60°,且MN=PN=500 m,求塔高AB.
参考答案:
1.答案:B
解析:如图15,AB为楼,CD为塔,AM为水平线,则有AB=20,
图15
∠DAM=45°,∠CAM=60°,
∴MD=20,AM=20,CM=20.
∴CD=20(1+)(m).
2.解:如图16,以AB为边,B为顶点作∠ABP=45°(点P在B点的东北方向上),射线BP即台风中心B的移动方向,以A点为圆心,300 km为半径画弧交射线BP于C,D两点,显然当台风中心从B点到达C点时,A点开始进入台风圈,台风中心在CD上移动的时间即为A处在台风圈中的时间.21cnjy.com
图16
设台风中心由B到C要t小时,在△ABC中,AB=400(km),AC=300(km),BC=40t(km), ∠ABC=45°,
由余弦定理,得
AC2=AB2+BC2-2AB·BC·cos∠ABC,
即3002=4002+(40t)2-2×400×40t·cos 45°.
∴4t2-40t+175=0.∴t==.
∴t1==5(h),t2-t1=-=5(h).
答:大约经过5h A进入台风圈,A处在台风圈中的时间为5 h.
3.解:在△ACD中,∠CAD=180°-∠ACD-∠ADC=60°,CD=6 000,∠ACD=45°,
由正弦定理,有AD==CD.
同理,在△BCD中,∠CBD=180°-∠BCD-∠BDC=135°,CD=6 000,∠BCD=30°.
由正弦定理,有BD==CD.
又在△ABD中,∠ADB=∠ADC+∠BDC=90°,
根据勾股定理,得
AB==·CD=CD=1 000(m).
答:炮兵阵地到目标的距离为1 000 m.
4.解:设AB的高为x.∵AB与地面垂直,
∴△ABM,△ABN,△ABP均为直角三角形.
∴BM=x·cot 30°=x,BN=x·cot 45°=x,BP=x·cot 60°=x.
在△MNB中,BM2=MN2+BN2-2MN·BN·cos∠MNB,
在△PNB中,BP2=NP2+BN2-2NP·BN·cos∠PNB,
又∵∠BNM与∠PNB互补,MN=NP=500,
∴3x2=250 000+x2-2×500x·cos∠MNB,①
x2=250 000+x2-2×500x·cos∠PNB.②
①+②,得x2=500 000+2x2,∴x=250(m).
答:塔高AB为250 m.
(设计者:李艳)
第2课时
导入新课
思路1.(探究导入)在解决实际问题中, ( http: / / www.21cnjy.com )经常涉及三角形问题,我们可以把它抽象为解三角形问题.本节课我们继续探究应用正弦定理、余弦定理解决与三角形有关的实际问题.
思路2.(直接导入)上两节课我们探究了怎 ( http: / / www.21cnjy.com )样测量到不可到达的点的距离,又解决了怎样测量底部不可到达的建筑物高度的问题,这些都是距离问题,本节课我们进一步探究综合运用正弦定理、余弦定理解决实际问题的方法步骤.
推进新课
①回忆前面是如何测量距离和高度的?
②在测量距离和高度时,是怎样由三角形的一些已知边和角来求其他边的?
③我们将实际问题转化为三角问题是按什么步骤来进行的?关键是什么?
④日常生活中还有一个例子,如航海, ( http: / / www.21cnjy.com )在浩瀚无垠的海面上如何确保轮船不迷失方向,同时保持一定的航速和航向前进,还有飞机在天空中飞行时如何确定地面上的目标等,这些可否像前面探究的距离和高度那样,转化为解三角形模型来解决呢?
活动:通过前面的学习,学生基本上熟悉了解决实际问题的方法步骤.这里仍要求学生回顾记忆,为了提高学生兴趣,可换个提法.前面解决实际问题的顺序是“实际问题→数学建模→数学模型的解→实际问题的解”,反映在解三角形上,教师可引导学生根据上节内容,用流程图表示出来.如图17,这里关键是找出已知量和未知量,画好平面示意图,确定需要解决的三角形.
图17
三角形模型应用很广泛,像航海确定方向等都离不开角,当然也就离不开解三角形,也就需要用正弦定理、余弦定理等有关的三角形知识来解决它.
讨论结果:①~④略.
例1 如图18,一艘海轮从A出发, ( http: / / www.21cnjy.com )沿北偏东75°的方向航行67.5 n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0 n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?(角度精确到0.1°,距离精确到0.01 n mile)
图18
活动:教师引导学生根据题意画出平面示意 ( http: / / www.21cnjy.com )图,这是解决本类题目很重要的一方面.教师可就此点拨学生注意:画图、用图、识图是学好数学的一项基本功,能否准确画出示意图直接决定着解题的成败,这项基本功较弱的同学可就此加强自己的补弱训练.我们前面学习时有过这样的经历:有些选择题,甚至解答题,只要画出示意图,解答结果很快就出来了,这就是数形结合的强大威力所在,提醒学生关注这一点.
解:在△ABC中,∠ABC=180°- 75°+ 32°=137°,根据余弦定理得,
AC=
=
≈113.15(n mile).
根据正弦定理得, =,
sin∠CAB==≈0.325 5,
所以∠CAB≈19.0°,75°-∠CAB=56.0°.
答:此船应该沿北偏东56.0°的方向航行,需要航行113.15 n mile.
点评:本例综合运用了正、余弦 ( http: / / www.21cnjy.com )定理,体现了正弦定理、余弦定理在解斜三角形中的重要作用.解完本例后教师引导学生进行反思领悟,让学生把重点放在数学建模这一共性上和对一般方法的掌握上.【出处:21教育名师】
变式训练
如图19,海中小岛A周围38 n mile内有暗礁,船正向南航行,在B处测得小岛A在船的南偏东30°,航行30 n mile到C处,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?【版权所有:21教育】
图19
解:在△ABC中,BC=30,B=30°,
∠ACB=180°-45°=135°,∴A=15°.
由正弦定理知=,
∴=.
∴AC==60cos 15°=(15+15)(n mile).
∴A到BC所在直线的距离为AC·sin 45°=(15+15)×=15(+1)≈40.98>38(n mile).21·cn·jy·com
∴不改变航向,继续向南航行,无触礁的危险.
例2图20是曲柄连杆机构的 ( http: / / www.21cnjy.com )示意图.当曲柄CB绕点C旋转时,通过连杆AB的传递,活塞做直线往复运动.当曲柄在CB0位置时,曲柄和连杆成一条直线,连杆的端点A在A0处.设连杆AB长为l mm,曲柄CB长为r mm,l>r.
图20
(1)当曲柄自CB0按顺时针方向旋转角为θ时,其中0°≤θ<360°,求活塞移动的距离(即连杆的端点A移动的距离A0A);
(2)当l=340 mm,r=85 mm,θ=80°时,求A0A的长(结果精确到1 mm).
活动:教师引导学生从实际问题中抽象出几何图 ( http: / / www.21cnjy.com )形,如图21所示,不难得到,活塞移动的距离为A0A=A0C-AC,易知A0C=AB+BC=l+r,所以,只要求出AC的长即可.在△ABC中,已知两边和其中一边的对角,可以通过正弦定理或余弦定理求出AC的长.
图21
解:(1)设AC=x,若θ=0°,则A0A=0;若θ=180°,则A0A=2r mm;若0°<θ<180°,在△ABC中,由余弦定理,得
AB2=AC2+BC2-2AC·BCcos C,[]
即x2-2(rcos θ)x-(l2-r2)=0.
解得x1=rcos θ+=(rcos θ+)(mm),
x2=rcos θ-<0(不合题意,舍去).
A0A=A0C-AC
=AB+BC-AC
=(l+r-rcos θ-)(mm).
若180°<θ<360°,则根据对称性,将上式中的θ改成360°-θ即可,有
A0A=(l+r-rcos θ-) mm.
总之,当0°≤θ<360°时,
A0A=(l+r-rcos θ-) mm.
(2)当l=340 mm,r=85 mm,θ=80°时,利用计算器算得
A0A=340+85-85cos 80°-
≈81(mm).
答:此时活塞移动的距离约为81 mm.
点评:解完本例后,教师引导学生进行反思总结, ( http: / / www.21cnjy.com )点拨学生运用正弦定理求A0A的长,并让学生比较两种方法的特点,体会正弦定理、余弦定理解题的异同.有的学生可能直接运用正弦定理解决本例或用两种方法给出本例的解答,对此教师要给予鼓励,提倡学生进行一题多解的训练.21教育网
例3 如图22所示,a是海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8 s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1.5 km/s.
图22
(1)设A到P的距离为x km,用x表示B,C到P的距离,并求x的值;
(2)求静止目标P到海防警戒线a的距离(结果精确到0.01 km).
活动:(1)PA,PB,PC长度之间的关系可 ( http: / / www.21cnjy.com )以通过收到信号的先后时间建立起来;(2)作PD⊥a,垂足为D,要求PD的长,只需要求出PA的长和cos∠APD,即cos∠PAB的值.由题意,PA-PB,PC-PB都是定值,因此,只需要分别在△PAB和△PAC中,求出cos∠PAB,cos∠PAC的表达式,建立方程即可.
解:(1)依题意,PA-PB=1.5×8=12(km),PC-PB=1.5×20=30(km).因此
PB=(x-12) km,PC=(18+x) km.
在△PAB中,AB=20 km,
cos∠PAB=
=
=.
同理,cos∠PAC=.
由于cos∠PAB=cos∠PAC,
即=,
解得x=(km).
(2)作PD⊥a,垂足为D.在Rt△PDA中,
PD=PAcos∠APD=PAcos∠PAB
=x·=≈17.71(km).
答:静止目标P到海防警戒线a的距离约为17.71 km.
点评:本例是本章教材中课本上 ( http: / / www.21cnjy.com )安排的最后一个例题,综合性较强.解完本题后教师应引导学生总结应用正弦定理、余弦定理解三角形的方法步骤.反思本例的解题方法,从方程思想出发,确定需要研究的三角形(一个或多个),运用余弦定理列出方程,这是解决本例问题的关键.【来源:21cnj*y.co*m】
变式训练
如图23,港口A北偏东30°方向 ( http: / / www.21cnjy.com )的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31 n mile,该轮船从B处沿正西方向航行20 n mile后到D处,测得CD为21 n mile,问此时轮船离港口A还有多远?21教育名师原创作品
图23
解:由条件知∠CAB=60°,设∠ACD=α,∠CDB=β.
在△BCD中,由余弦定理,得
cos β==-.
∴sin β==.
∴sin α=sin(β-60°)=sin βcos 60°-cos βsin 60°=.
在△ACD中由正弦定理,得=,
∴AD==15(n mile).
答:此时轮船离港口还有15 n mile.
课本本节练习1,2.
先让学生回顾本节所探究的有关角度的知识过程 ( http: / / www.21cnjy.com ),回顾在本节实际问题的探究中,是如何将实际问题转化为数学问题的,又是怎样灵活地选用正弦定理、余弦定理建立数学模型的.
通过本节例题的探究,我们感受到数学模型可以有效地描述自然现象和社会现象;数学是人类的一种文化,它的内容、思想、方法和语言是现代文明的重要组成部分.
1.课本本节习题2—3 B组1,2.
2.阅读本章小结建议.
本教案是根据课程标准、学生的认知特点、内容的安排而设计的,由于本节课的前面已经有了一节课的举例探究经验,因此设计的活动主要都是通过学生自己完成.学生对图形难以把握,特别从空间的视角去审视的时候有些困难.因此教师应充分利用多媒体课件演示,让学生从动态中发现实物背景下的数学图形及有关的角度问题,引导学生自己画出平面示意图——这是解决本例的关键所在,教师不要怕在此浪费时间.www-2-1-cnjy-com
本教案的设计意图还在于,通过本节课的展 ( http: / / www.21cnjy.com )示,让学生体会到数学离不开生活,生活离不开数学,数学知识来源于生活而最终服务于生活;数学课堂的最后呈现标准不是学生成为解题能手,而是让学生体会到数学的实用价值. 21*cnjy*com
一、备用习题
1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系是( ).
A.α>β B.α=β
C.α+β=90° D.α+β=180°
2.已知两座灯塔A和B与海洋观察站 ( http: / / www.21cnjy.com )C的距离相等,灯塔A在观察站C的北偏东40°,灯塔B在观察站C的南偏东60°,则灯塔A在灯塔B的( ).21世纪教育网版权所有
A.北偏东10° B.北偏西10°
C.南偏东10° D.南偏西10°
3.从地面上观察一建在山顶上的建筑物,从观测点看建筑物底部到顶部的角度为α,同时测得建筑物顶部仰角为β,则山顶的仰角为( ).
A.α+β B.α-β
C.β-α D.α
4.有一长为100 m的斜坡,它的倾斜角为45°,现在要把倾斜角改成30°,则坡度要伸长__________ m.www.21-cn-jy.com
5.如图24,有两条相交成60° ( http: / / www.21cnjy.com )角的直线XX′,YY′,交点是O,甲、乙分别在OX,OY上,起初甲在离O点3 km的A点,乙在离O点1 km的B点,后来两人同时以每小时4 km的速度,甲沿XX′方向,乙沿Y′Y方向步行,
(1)起初,两人的距离是多少?
(2)用包含t的式子表示t h后两人的距离;
(3)什么时候两人的距离最短?
图24 图25
6.如图25,当甲船位于A处时获悉,在 ( http: / / www.21cnjy.com )其正东方向相距20 n mile的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10 n mile的C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1°).
参考答案:
1.B
2.B
3.C
4.50(-)
5.解:(1)∵甲,乙两人起初的位置分别是A,B,则
AB2=OA2+OB2-2OA·OBcos60°=32+12-2×3×1×=7,
∴起初,两人的距离是 km.
(2)设甲,乙两人t h后的位置分别是P,Q,则AP=4t,BQ=4t.
当0≤t≤时,PQ2=(3-4t)2+(1+4t)2-2(3-4t)(1+4t)cos60°=48t2-24t+7;
当t>时,PQ2=(4t-3)2+(1+4t)2-2(4t-3)(1+4t)cos120°=48t2-24t+7,
∴PQ=.
(3)PQ2=48t2-24t+7=48(t-)2+4,
∴当t=时,即在第15分钟末,PQ最短.
答:在第15分钟末,两人的距离最短.
6.解:连接BC,由余弦定理,得
BC2=202+102-2×20×10×cos 120°=700,
于是BC=10.
由=,
∴sin∠ACB=.
∵∠ACB<90°,∴∠ACB≈41°.
∴乙船应朝北偏东71°方向沿直线前往B处救援.
二、测量问题中的有关名词和术语
(1)坡度(坡比)与坡角:
如图26,把坡面的铅直高度h和水平 ( http: / / www.21cnjy.com )宽度l的比叫作坡度(或叫作坡比),用字母i表示,即i=.坡度一般写成h∶l的形式.坡面与水平面的夹角α叫作坡角,坡角与坡度之间有如下关系:i==tan α.【来源:21·世纪·教育·网】
图26 图27
(2)仰角与俯角:
如图27,以水平线为基准,视线在水平线上方所成的角叫作仰角,视线在水平线下方所成的角叫作俯角.
(3)方向角与方位角:
方向角:如图28,把指北或指南的方向 ( http: / / www.21cnjy.com )线与目标方向线所成的小于90°的水平角,叫作方向角.目标方向线的方向一般可用“×偏×多少度”来表示,这里第一个“×”号是“北”或“南”字,第二个“×”是“东”或“西”字.如图28中OA,OB,OC,OD的方向角分别为北偏东60°,北偏西45°(或西北方向),南偏西30°,南偏东40°.
方位角:某点开始的指北方向线按顺时针方向转到目标方向线为止的水平角,叫作方位角.
图28 图29
(4)水平距离、垂直距离、坡面距离:
如图29,BC代表水平距离,AC代表垂直距离,AB代表坡面距离.
(设计者:李艳)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
教学设计
3 解三角形的实际应用举例
教学分析
本节重点研究底部不可到达的高度测量问题, ( http: / / www.21cnjy.com )这类问题在我们的日常生活中比比皆是,学生对实际背景非常熟悉,这给教学带来了极大的便利.由于底部不可到达,这类问题不能直接用解直角三角形的方法来解决,但用正弦定理和余弦定理就可以计算出建筑物顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.教学时要充分利用多媒体课件给学生以动态演示,加强直观感知.
本节课主要是测量问题,一是要熟悉仰角、俯角的意义,二是要会在几个三角形中找出已知量与未知量之间的关系,逐步转化,最终归结为解三角形的问题.
三维目标
1.结合实际测量工具,能用正弦定理、余弦定理等知识解决生活中一些有关底部不可到达的物体高度的测量问题.
2.使学生体会数学知识来源于生活并应用于生 ( http: / / www.21cnjy.com )活,进一步培养学生学习数学、应用数学的意识以及观察、归纳、类比、概括的能力.提高灵活地选择正弦定理、余弦定理的解题能力.
3.通过本节的探究,引导学生经过自己的数学 ( http: / / www.21cnjy.com )活动,从实际问题中提取数学模型,使学生经历发现和创造过程,进一步拓展学生的数学活动空间,发展学生“做数学”“用数学”的意识.
重点难点
教学重点:分析测量物体高度 ( http: / / www.21cnjy.com )问题的实际背景,正确运用正弦定理、余弦定理解决底部不可到达的测量物体高度的问题,进一步熟悉数学建模的方法步骤,熟悉解决实际问题的规范的解题过程.
教学难点:将测量底部不可到达物体的高度问题转化为数学问题是本节的难点,另一个难点是灵活选用正弦定理和余弦定理.
课时安排
2课时
第1课时
导入新课
思路1.(问题导入)现实生活中,人们又 ( http: / / www.21cnjy.com )是怎样测量底部不可到达的建筑物高度的呢?通过学习本节你将轻松愉快地测量出山高和工厂的烟囱高,在学生踊跃的状态下展开新课.或者先让学生说一说我们校园内水塔的高度测量问题,在学生纷纷寻求测量水塔高度的方法争论中自然地引入新课.
思路2.(情境导入)你有坐汽车(或 ( http: / / www.21cnjy.com )者火车)经过山前水平公路的经历吗?如果身边带着测角仪,那么根据路标(100米杆)就会立即测算出你所看到的山的高度.利用正弦定理、余弦定理你也会马上算出来,在学生急切想知道如何测算山高的期待中展开新课.
推进新课
①回忆正弦定理、余弦定理,并提出已知三角形的两边及一边的对角选用哪个定理?,
②怎样将实际问题转化为解三角形问题?
③如果底部可到达,如电线杆的高度应怎样测量?如果底部不能到达,如工厂的烟囱的高度应怎样测量呢?
④对解题中的近似值怎样处理才能减小误差呢?
活动:教师先让学生回忆正弦定理、余 ( http: / / www.21cnjy.com )弦定理的内容,学生很快回忆起来,若已知三角形的两边及其中一边的对角先用正弦定理较好.引导学生回忆数学建模的方法步骤:分析→建模→求解→检验,鼓励学生多动手画图.特别是对想象能力较弱的学生,更应画出图形,在图形上标出已知的数据以加强直观感知.21·世纪*教育网
对于底部可到达的物体的高度问题,如测量电线杆 ( http: / / www.21cnjy.com )的高度,利用初中的知识即可解决.如图1,只要测出∠B及BC即可算出AC的高度.对底部不能到达的物体的高度怎样测量呢?
图1 图2[]
教师引导学生分组讨论,充分 ( http: / / www.21cnjy.com )发挥学生的想象力.学生会提出许多的方案.教师可一一指导,选出其中有代表性的方案作为本节教学的切入点,比如有的学生会提出:既然底部不可到达则BC就不可测出,但作为解三角形的条件至少需有一边,如此可否在原来的B点后退至B′点,测量BB′的距离.如图2,引导学生深入探究,效果将会很好.
在具体解题过程中,教师可 ( http: / / www.21cnjy.com )针对解题中的近似值处理问题,适时地提醒学生注意:(1)应根据题中对精确度的要求,合理选择近似值.(2)为避免误差的积累,解题过程中应尽可能地使用原始(已知)数据,少用间接求出的量.2-1-c-n-j-y
讨论结果:①~④略.
例1 如图3所示,两点C,D与烟囱底部 ( http: / / www.21cnjy.com )在同一水平直线上,在点C1,D1,利用高为1.5 m 的测角仪器测得烟囱的仰角分别是α=45°和β=60°,C,D间的距离是12 m.计算烟囱的高AB(结果精确到0.01 m).
图3 图4
解:在△BC1D1中,∠BD1C1=180°-60°=120°,∠C1BD1=60°-45°=15°,由正弦定理,得
=,
BC1===(18+6)(m),
从而A1B=BC1=18+6≈28.392(m),
因此AB=A1B+AA1≈28.392+1.5=29.892≈29.89(m).
答:烟囱的高约为29.89 m.
点评:这样我们就设计出一种测量底部不可 ( http: / / www.21cnjy.com )到达的建筑物的高度的方法,利用测角仪器和长度测量工具即可完成,即要测量某一高度AB,只要在地面某一条直线上取两点D,C,量出CD的长a,并在C,D两点测出B的仰角α,β,则高度AB=+h,其中h为测角仪器的高.
变式训练
如图5,B,C,D三点在地面同一直线上,DC=a,从C、D两点测得A点的仰角分别是β,α(α<β),则A点离地面的高AB等于( ).
图5
A. B. C. D.
答案:C
例2 如图6,在山顶铁塔上B处测得 ( http: / / www.21cnjy.com )地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′.已知铁塔BC部分的高为27.3 m,求出山高CD(精确到0.1 m).
图6 图7
活动:本题实际上是上例的变式训练.
教师引导学生观察图形,弄清俯角是什么意思 ( http: / / www.21cnjy.com ).假若把该图以D为支点逆时针旋转90°,如图7,让学生观察此图与例1图形的异同.教师要给学生留出一定的探究时间,让学生充分讨论思考,学生会发现,例1、例2两题图形的形状是一致的,这里易知∠ABC=90°-α,∠ACB=90°+β及BC=27.3 m,而求CD(如图7).学生只要探究到这步,以下的问题可完全由学生自己解决,教师只是点拨其解题步骤的书写及近似值的确定即可.[]
解:在△ABC中,∠BCA=90°+β,∠ABC=90°-α,∠BAC=α-β,∠BAD=α.
根据正弦定理,=,
所以AB==.
解Rt△ABD,得BD=ABsin∠BAD=.
将测量数据代入上式,得
BD==≈176.5(m),
CD=BD-BC≈176.5-27.3≈149.2(m).
答:山的高度约为149.2 m.
点评:本题学生也可能这样求解:先在△ABC中求得AC,再在Rt△ACD中直接求得CD,教师应鼓励学生这样思考很好,更直接.2·1·c·n·j·y
变式训练
有一长为10 m的斜坡,它的倾斜角是75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延伸( ).
A.5 m B.10 m
C.10 m D.10 m
解析:如图8,在△ABC中,设BC=x m,由正弦定理,可知
图8
=,
∴x=10(m).
答案:C
例3 如图9,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15°的方向上,行驶5 km后到达B处,测得此山顶在西偏北25°的方向上,仰角为8°,求此山的高度CD.(sin 15 °≈0.258 8,sin 10°≈0.173 6,tan 8°≈0.140 5)
图9
活动:教师引导学生充分理解题目背景, ( http: / / www.21cnjy.com )引导学生画出图形.首先理解什么是仰角,西偏北25°是什么意思.本题的图形是一个立体几何图形,让学生充分理解图形中的各个已知量和要求的量.
解:在△ABC中,∠CAB=15°,∠ACB=25°-15°=10°,
根据正弦定理,=,BC==≈7.453 9(km),
CD=BC×tan∠DBC≈BC×tan 8°≈1 047(m).
答:山的高度约为1 047 m.
点评:本例中三角形较多,要根据已知条件及所求的边长恰当选取我们需要的三角形.
变式训练
如图10,地平面上有一旗杆OP,为了测 ( http: / / www.21cnjy.com )得它的高度h,在地面上选一基线AB,AB=20 m,在A点处测得P点的仰角∠OAP=30°,在B点处测得P点的仰角∠OBP=45°,又测得∠AOB=60°,求旗杆的高度h(结果保留两个有效数字).
图10
活动:在看图时要注意结合实际— ( http: / / www.21cnjy.com )—旗杆OP垂直地面,所以△AOP和△BOP都是直角三角形.又这两个三角形中各已知一个锐角,那么其他各边均可用h的代数式表示.在△AOB中,已知一边及其对角,另两边均为h的代数式,可利用余弦定理构造方程,解这个方程即可求出旗杆高h.
解:在Rt△AOP中,∠OAP=30°,OP=h,
∴OA=OP·cot 30°=h.
在Rt△BOP中,∠OBP=45°,
∴OB=OP=h.
在△AOB中,AB=20,∠AOB=60°,
由余弦定理,得
AB2=OA2+OB2-2×OA×OB·cos 60°,
即202=(h)2+h2-2·h·h·.
解得h2=≈176.4,∴h≈13(m).
答:旗杆高度约为13 m.
点评:(1)仰角和俯角是在同一铅垂面内视线与水平线的夹角,当视线在水平线之上时称为仰角,当视线在水平线之下时称为俯角.21*cnjy*com
(2)由余弦定理(正弦定理)构造方程,是解决此问题的关键.方程思想是解决问题的一种常用思想方法.[]
例4自动卸货汽车采用液压机构.设计时需 ( http: / / www.21cnjy.com )要计算油泵顶杠BC的长度,如图11所示.已知车厢的最大仰角为60°(指车厢AC与水平线夹角),油泵顶点B与车厢支点A之间的距离为1.95 m,AB与水平线之间的夹角为6°20′,AC长为1.40 m.计算BC的长度(结果精确到0.01 m).
图11 图12
活动:本例是一道经典例题,教师引导学生先观察实物模型,通过阅读题意画出几何图形.
这个问题就是在△ABC(如图12)中,已知AB=1.95 m,AC=1.40 m,∠BAC=60°+6°20′=66°20′,求BC的长.
解:由余弦定理,得
BC2=AB2+AC2-2AB·ACcos A
=1.952+1.402-2×1.95×1.40cos 66°20′[]
≈3.571,
所以BC≈1.89(m).
答:顶杆BC约长1.89 m.
课本本节练习1,2.
先由学生自己回顾本节所学的测量底部不可到达 ( http: / / www.21cnjy.com )的建筑物高度的方法,是如何从实际问题情境中寻求到解决问题的方案的?你是否能根据题意准确地画出示意图?你没有画出的原因是什么?
在学生自己总结归纳,对本节有 ( http: / / www.21cnjy.com )了一个整体认识的时候,教师可作进一步的归纳.解决实际问题的关键是建立数学模型,特别是画出示意图是准确迅速解这个数学问题的关键,也是本节要体现的技能,这在高考中体现得很突出,需要在反复的练习和动手操作中提高这方面的能力.
课本习题2-3 A组4.
本教案设计以情境教学、问题教学为主,教 ( http: / / www.21cnjy.com )师引导和学生积极参与探究相结合,充分体现以学为主、逐步领悟的原则.日常生活中的实例体现了数学知识的生动运用.通过合作学习和相互提问补充的方法让学生多感受问题的演变过程,通过多媒体课件的演示让学生切身感受实际问题所反映的数学本质,让学生在轻松愉快的互动气氛中学到知识,提高能力.
本教案设计的中心主线是在学生探究活动中 ( http: / / www.21cnjy.com )提炼数学建模,不要求学生死记硬背解决实际问题的方法步骤.本教案的设计始终抓住本节乃至本章的这一重点,不在一些细枝末节上浪费时间.
通过本节及上节的探究,学生基本上熟悉了解决实际问题的思想方法,下一步教师要在规范步骤等方面加以关注.
备用习题
1.在一幢20m高的楼顶测得对面一塔顶的仰角为60°,塔基的俯角为45°,则塔高为( ).
A.20(1+) m B.20(1+) m
C.10(+) m D.20(+) m
2.在某时刻,A点西400 km的B处是 ( http: / / www.21cnjy.com )台风中心,台风以每小时40 km的速度向东北方向直线前进,以台风中心为圆心、300 km为半径的圆称为“台风圈”,从此时刻算起,大约经过多长时间A进入台风圈?A处在台风圈中的时间有多长(结果保留根号)
3.如图13,我炮兵阵地位于地面A处,两观察 ( http: / / www.21cnjy.com )所分别位于地面点C和D处,已知CD=6 000 m,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°,求炮兵阵地到目标的距离(结果保留根号).
图13 图14
4.如图14,测量人员沿直线MNP的 ( http: / / www.21cnjy.com )方向测量,测得A点的仰角分别是∠AMB=30°,∠ANB=45°,∠APB=60°,且MN=PN=500 m,求塔高AB.
参考答案:
1.答案:B
解析:如图15,AB为楼,CD为塔,AM为水平线,则有AB=20,
图15
∠DAM=45°,∠CAM=60°,
∴MD=20,AM=20,CM=20.
∴CD=20(1+)(m).
2.解:如图16,以AB为边,B为顶点作∠ABP=45°(点P在B点的东北方向上),射线BP即台风中心B的移动方向,以A点为圆心,300 km为半径画弧交射线BP于C,D两点,显然当台风中心从B点到达C点时,A点开始进入台风圈,台风中心在CD上移动的时间即为A处在台风圈中的时间.21cnjy.com
图16
设台风中心由B到C要t小时,在△ABC中,AB=400(km),AC=300(km),BC=40t(km), ∠ABC=45°,
由余弦定理,得
AC2=AB2+BC2-2AB·BC·cos∠ABC,
即3002=4002+(40t)2-2×400×40t·cos 45°.
∴4t2-40t+175=0.∴t==.
∴t1==5(h),t2-t1=-=5(h).
答:大约经过5h A进入台风圈,A处在台风圈中的时间为5 h.
3.解:在△ACD中,∠CAD=180°-∠ACD-∠ADC=60°,CD=6 000,∠ACD=45°,
由正弦定理,有AD==CD.
同理,在△BCD中,∠CBD=180°-∠BCD-∠BDC=135°,CD=6 000,∠BCD=30°.
由正弦定理,有BD==CD.
又在△ABD中,∠ADB=∠ADC+∠BDC=90°,
根据勾股定理,得
AB==·CD=CD=1 000(m).
答:炮兵阵地到目标的距离为1 000 m.
4.解:设AB的高为x.∵AB与地面垂直,
∴△ABM,△ABN,△ABP均为直角三角形.
∴BM=x·cot 30°=x,BN=x·cot 45°=x,BP=x·cot 60°=x.
在△MNB中,BM2=MN2+BN2-2MN·BN·cos∠MNB,
在△PNB中,BP2=NP2+BN2-2NP·BN·cos∠PNB,
又∵∠BNM与∠PNB互补,MN=NP=500,
∴3x2=250 000+x2-2×500x·cos∠MNB,①
x2=250 000+x2-2×500x·cos∠PNB.②
①+②,得x2=500 000+2x2,∴x=250(m).
答:塔高AB为250 m.
(设计者:李艳)
第2课时
导入新课
思路1.(探究导入)在解决实际问题中, ( http: / / www.21cnjy.com )经常涉及三角形问题,我们可以把它抽象为解三角形问题.本节课我们继续探究应用正弦定理、余弦定理解决与三角形有关的实际问题.
思路2.(直接导入)上两节课我们探究了怎 ( http: / / www.21cnjy.com )样测量到不可到达的点的距离,又解决了怎样测量底部不可到达的建筑物高度的问题,这些都是距离问题,本节课我们进一步探究综合运用正弦定理、余弦定理解决实际问题的方法步骤.
推进新课
①回忆前面是如何测量距离和高度的?
②在测量距离和高度时,是怎样由三角形的一些已知边和角来求其他边的?
③我们将实际问题转化为三角问题是按什么步骤来进行的?关键是什么?
④日常生活中还有一个例子,如航海, ( http: / / www.21cnjy.com )在浩瀚无垠的海面上如何确保轮船不迷失方向,同时保持一定的航速和航向前进,还有飞机在天空中飞行时如何确定地面上的目标等,这些可否像前面探究的距离和高度那样,转化为解三角形模型来解决呢?
活动:通过前面的学习,学生基本上熟悉了解决实际问题的方法步骤.这里仍要求学生回顾记忆,为了提高学生兴趣,可换个提法.前面解决实际问题的顺序是“实际问题→数学建模→数学模型的解→实际问题的解”,反映在解三角形上,教师可引导学生根据上节内容,用流程图表示出来.如图17,这里关键是找出已知量和未知量,画好平面示意图,确定需要解决的三角形.
图17
三角形模型应用很广泛,像航海确定方向等都离不开角,当然也就离不开解三角形,也就需要用正弦定理、余弦定理等有关的三角形知识来解决它.
讨论结果:①~④略.
例1 如图18,一艘海轮从A出发, ( http: / / www.21cnjy.com )沿北偏东75°的方向航行67.5 n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0 n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?(角度精确到0.1°,距离精确到0.01 n mile)
图18
活动:教师引导学生根据题意画出平面示意 ( http: / / www.21cnjy.com )图,这是解决本类题目很重要的一方面.教师可就此点拨学生注意:画图、用图、识图是学好数学的一项基本功,能否准确画出示意图直接决定着解题的成败,这项基本功较弱的同学可就此加强自己的补弱训练.我们前面学习时有过这样的经历:有些选择题,甚至解答题,只要画出示意图,解答结果很快就出来了,这就是数形结合的强大威力所在,提醒学生关注这一点.
解:在△ABC中,∠ABC=180°- 75°+ 32°=137°,根据余弦定理得,
AC=
=
≈113.15(n mile).
根据正弦定理得, =,
sin∠CAB==≈0.325 5,
所以∠CAB≈19.0°,75°-∠CAB=56.0°.
答:此船应该沿北偏东56.0°的方向航行,需要航行113.15 n mile.
点评:本例综合运用了正、余弦 ( http: / / www.21cnjy.com )定理,体现了正弦定理、余弦定理在解斜三角形中的重要作用.解完本例后教师引导学生进行反思领悟,让学生把重点放在数学建模这一共性上和对一般方法的掌握上.【出处:21教育名师】
变式训练
如图19,海中小岛A周围38 n mile内有暗礁,船正向南航行,在B处测得小岛A在船的南偏东30°,航行30 n mile到C处,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?【版权所有:21教育】
图19
解:在△ABC中,BC=30,B=30°,
∠ACB=180°-45°=135°,∴A=15°.
由正弦定理知=,
∴=.
∴AC==60cos 15°=(15+15)(n mile).
∴A到BC所在直线的距离为AC·sin 45°=(15+15)×=15(+1)≈40.98>38(n mile).21·cn·jy·com
∴不改变航向,继续向南航行,无触礁的危险.
例2图20是曲柄连杆机构的 ( http: / / www.21cnjy.com )示意图.当曲柄CB绕点C旋转时,通过连杆AB的传递,活塞做直线往复运动.当曲柄在CB0位置时,曲柄和连杆成一条直线,连杆的端点A在A0处.设连杆AB长为l mm,曲柄CB长为r mm,l>r.
图20
(1)当曲柄自CB0按顺时针方向旋转角为θ时,其中0°≤θ<360°,求活塞移动的距离(即连杆的端点A移动的距离A0A);
(2)当l=340 mm,r=85 mm,θ=80°时,求A0A的长(结果精确到1 mm).
活动:教师引导学生从实际问题中抽象出几何图 ( http: / / www.21cnjy.com )形,如图21所示,不难得到,活塞移动的距离为A0A=A0C-AC,易知A0C=AB+BC=l+r,所以,只要求出AC的长即可.在△ABC中,已知两边和其中一边的对角,可以通过正弦定理或余弦定理求出AC的长.
图21
解:(1)设AC=x,若θ=0°,则A0A=0;若θ=180°,则A0A=2r mm;若0°<θ<180°,在△ABC中,由余弦定理,得
AB2=AC2+BC2-2AC·BCcos C,[]
即x2-2(rcos θ)x-(l2-r2)=0.
解得x1=rcos θ+=(rcos θ+)(mm),
x2=rcos θ-<0(不合题意,舍去).
A0A=A0C-AC
=AB+BC-AC
=(l+r-rcos θ-)(mm).
若180°<θ<360°,则根据对称性,将上式中的θ改成360°-θ即可,有
A0A=(l+r-rcos θ-) mm.
总之,当0°≤θ<360°时,
A0A=(l+r-rcos θ-) mm.
(2)当l=340 mm,r=85 mm,θ=80°时,利用计算器算得
A0A=340+85-85cos 80°-
≈81(mm).
答:此时活塞移动的距离约为81 mm.
点评:解完本例后,教师引导学生进行反思总结, ( http: / / www.21cnjy.com )点拨学生运用正弦定理求A0A的长,并让学生比较两种方法的特点,体会正弦定理、余弦定理解题的异同.有的学生可能直接运用正弦定理解决本例或用两种方法给出本例的解答,对此教师要给予鼓励,提倡学生进行一题多解的训练.21教育网
例3 如图22所示,a是海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8 s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1.5 km/s.
图22
(1)设A到P的距离为x km,用x表示B,C到P的距离,并求x的值;
(2)求静止目标P到海防警戒线a的距离(结果精确到0.01 km).
活动:(1)PA,PB,PC长度之间的关系可 ( http: / / www.21cnjy.com )以通过收到信号的先后时间建立起来;(2)作PD⊥a,垂足为D,要求PD的长,只需要求出PA的长和cos∠APD,即cos∠PAB的值.由题意,PA-PB,PC-PB都是定值,因此,只需要分别在△PAB和△PAC中,求出cos∠PAB,cos∠PAC的表达式,建立方程即可.
解:(1)依题意,PA-PB=1.5×8=12(km),PC-PB=1.5×20=30(km).因此
PB=(x-12) km,PC=(18+x) km.
在△PAB中,AB=20 km,
cos∠PAB=
=
=.
同理,cos∠PAC=.
由于cos∠PAB=cos∠PAC,
即=,
解得x=(km).
(2)作PD⊥a,垂足为D.在Rt△PDA中,
PD=PAcos∠APD=PAcos∠PAB
=x·=≈17.71(km).
答:静止目标P到海防警戒线a的距离约为17.71 km.
点评:本例是本章教材中课本上 ( http: / / www.21cnjy.com )安排的最后一个例题,综合性较强.解完本题后教师应引导学生总结应用正弦定理、余弦定理解三角形的方法步骤.反思本例的解题方法,从方程思想出发,确定需要研究的三角形(一个或多个),运用余弦定理列出方程,这是解决本例问题的关键.【来源:21cnj*y.co*m】
变式训练
如图23,港口A北偏东30°方向 ( http: / / www.21cnjy.com )的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31 n mile,该轮船从B处沿正西方向航行20 n mile后到D处,测得CD为21 n mile,问此时轮船离港口A还有多远?21教育名师原创作品
图23
解:由条件知∠CAB=60°,设∠ACD=α,∠CDB=β.
在△BCD中,由余弦定理,得
cos β==-.
∴sin β==.
∴sin α=sin(β-60°)=sin βcos 60°-cos βsin 60°=.
在△ACD中由正弦定理,得=,
∴AD==15(n mile).
答:此时轮船离港口还有15 n mile.
课本本节练习1,2.
先让学生回顾本节所探究的有关角度的知识过程 ( http: / / www.21cnjy.com ),回顾在本节实际问题的探究中,是如何将实际问题转化为数学问题的,又是怎样灵活地选用正弦定理、余弦定理建立数学模型的.
通过本节例题的探究,我们感受到数学模型可以有效地描述自然现象和社会现象;数学是人类的一种文化,它的内容、思想、方法和语言是现代文明的重要组成部分.
1.课本本节习题2—3 B组1,2.
2.阅读本章小结建议.
本教案是根据课程标准、学生的认知特点、内容的安排而设计的,由于本节课的前面已经有了一节课的举例探究经验,因此设计的活动主要都是通过学生自己完成.学生对图形难以把握,特别从空间的视角去审视的时候有些困难.因此教师应充分利用多媒体课件演示,让学生从动态中发现实物背景下的数学图形及有关的角度问题,引导学生自己画出平面示意图——这是解决本例的关键所在,教师不要怕在此浪费时间.www-2-1-cnjy-com
本教案的设计意图还在于,通过本节课的展 ( http: / / www.21cnjy.com )示,让学生体会到数学离不开生活,生活离不开数学,数学知识来源于生活而最终服务于生活;数学课堂的最后呈现标准不是学生成为解题能手,而是让学生体会到数学的实用价值. 21*cnjy*com
一、备用习题
1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系是( ).
A.α>β B.α=β
C.α+β=90° D.α+β=180°
2.已知两座灯塔A和B与海洋观察站 ( http: / / www.21cnjy.com )C的距离相等,灯塔A在观察站C的北偏东40°,灯塔B在观察站C的南偏东60°,则灯塔A在灯塔B的( ).21世纪教育网版权所有
A.北偏东10° B.北偏西10°
C.南偏东10° D.南偏西10°
3.从地面上观察一建在山顶上的建筑物,从观测点看建筑物底部到顶部的角度为α,同时测得建筑物顶部仰角为β,则山顶的仰角为( ).
A.α+β B.α-β
C.β-α D.α
4.有一长为100 m的斜坡,它的倾斜角为45°,现在要把倾斜角改成30°,则坡度要伸长__________ m.www.21-cn-jy.com
5.如图24,有两条相交成60° ( http: / / www.21cnjy.com )角的直线XX′,YY′,交点是O,甲、乙分别在OX,OY上,起初甲在离O点3 km的A点,乙在离O点1 km的B点,后来两人同时以每小时4 km的速度,甲沿XX′方向,乙沿Y′Y方向步行,
(1)起初,两人的距离是多少?
(2)用包含t的式子表示t h后两人的距离;
(3)什么时候两人的距离最短?
图24 图25
6.如图25,当甲船位于A处时获悉,在 ( http: / / www.21cnjy.com )其正东方向相距20 n mile的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10 n mile的C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1°).
参考答案:
1.B
2.B
3.C
4.50(-)
5.解:(1)∵甲,乙两人起初的位置分别是A,B,则
AB2=OA2+OB2-2OA·OBcos60°=32+12-2×3×1×=7,
∴起初,两人的距离是 km.
(2)设甲,乙两人t h后的位置分别是P,Q,则AP=4t,BQ=4t.
当0≤t≤时,PQ2=(3-4t)2+(1+4t)2-2(3-4t)(1+4t)cos60°=48t2-24t+7;
当t>时,PQ2=(4t-3)2+(1+4t)2-2(4t-3)(1+4t)cos120°=48t2-24t+7,
∴PQ=.
(3)PQ2=48t2-24t+7=48(t-)2+4,
∴当t=时,即在第15分钟末,PQ最短.
答:在第15分钟末,两人的距离最短.
6.解:连接BC,由余弦定理,得
BC2=202+102-2×20×10×cos 120°=700,
于是BC=10.
由=,
∴sin∠ACB=.
∵∠ACB<90°,∴∠ACB≈41°.
∴乙船应朝北偏东71°方向沿直线前往B处救援.
二、测量问题中的有关名词和术语
(1)坡度(坡比)与坡角:
如图26,把坡面的铅直高度h和水平 ( http: / / www.21cnjy.com )宽度l的比叫作坡度(或叫作坡比),用字母i表示,即i=.坡度一般写成h∶l的形式.坡面与水平面的夹角α叫作坡角,坡角与坡度之间有如下关系:i==tan α.【来源:21·世纪·教育·网】
图26 图27
(2)仰角与俯角:
如图27,以水平线为基准,视线在水平线上方所成的角叫作仰角,视线在水平线下方所成的角叫作俯角.
(3)方向角与方位角:
方向角:如图28,把指北或指南的方向 ( http: / / www.21cnjy.com )线与目标方向线所成的小于90°的水平角,叫作方向角.目标方向线的方向一般可用“×偏×多少度”来表示,这里第一个“×”号是“北”或“南”字,第二个“×”是“东”或“西”字.如图28中OA,OB,OC,OD的方向角分别为北偏东60°,北偏西45°(或西北方向),南偏西30°,南偏东40°.
方位角:某点开始的指北方向线按顺时针方向转到目标方向线为止的水平角,叫作方位角.
图28 图29
(4)水平距离、垂直距离、坡面距离:
如图29,BC代表水平距离,AC代表垂直距离,AB代表坡面距离.
(设计者:李艳)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
