苏教版三年级下册数学有趣的乘法计算教学课件(共22张PPT)
文档属性
| 名称 | 苏教版三年级下册数学有趣的乘法计算教学课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-08 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
有趣的乘法计算
苏教版三年级数学下册
吓人的算式
625431534127×11=
?
有规律
大事起于难,小事起于易,必作于细,必成于易。
——春秋时期《道德经》
你知道吗?
解决困难要从容易的地方入手
做成大事要从小事入手
24
24
264
53
53
583
24
× 11
53
×11
62
×11
62
62
682
简单的背后
笔算 24×11 53×11 62×11
24
× 11
24
24
264
53
×11
53
53
583
62
×11
62
62
682
观察比较
小组交流:
(1)得到的积与原来的哪个乘数有关?
(2)比较积的每一位数与这个乘数的每一位比较,你有什么发现?
24
× 11
24
24
264
53
×11
53
53
583
62
×11
62
62
682
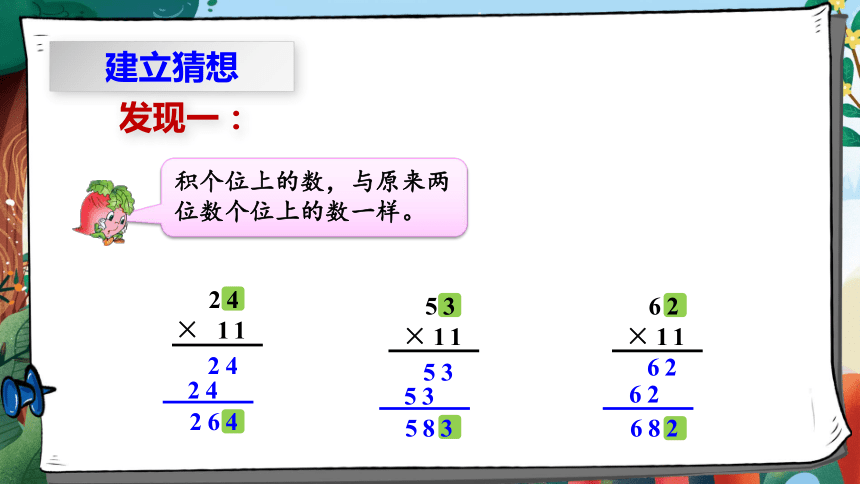
积个位上的数,与原来两位数个位上的数一样。
建立猜想
发现一:
24
× 11
24
24
264
53
×11
53
53
583
62
×11
62
62
682
积百位上的数,与原来两位数十位上的数一样。
建立猜想
发现二:
24
× 11
24
24
264
53
×11
53
53
583
62
×11
62
62
682
6=2+4
8=5+3
8=6+2
积十位上的数, 等于原来两位数个位与十位上数的和。
建立猜想
发现三:
一个两位数与11相乘
积的个位上的数与原来两位数的个位上的数相同,
积的百位上的数与原来两位数的十位上的数相同,
积的十位上的数是原来两位数个位与十位上的数之和。
口诀记忆:两头一拉,中间相加;
我们的猜想
根据你的发现试着完成下面的填空, 再用竖式计算验证。
23 × 11 = 2 3
64 × 11 = 4
59 × 11 = 9
5
我们的猜想
23
× 11
23
23
253
验证:
根据你的发现试着完成下面的填空, 再用竖式计算验证。
23 × 11 = 2 3
64 × 11 = 4
59 × 11 = 9
5
当个位和十位上的数相加满10时, 该怎样做?
7
0
6
4
十位满十,百位加一。
6+4=10
5+9=14
我们的猜想
23 × 11 = 2 3
64 × 11 = 4
59 × 11 = 9
5
7
0
6
4
23
× 11
23
23
253
64
× 11
64
64
704
59
× 11
59
59
649
验证:
通过验证,发现我们的猜想是正确的。
一个两位数与11相乘:
积的个位上的数与原来两位数的个位上的数相同
积的百位上的数与原来两位数的十位上的数相同,
积的十位上的数是原来两位数个位与十位上的数之和。
口诀: 两头一拉,中间相加;
十位满十,百位加一。
我们的猜想
当两位数个位与十位上的数相加满10时,积的十位上写和的个位数字,向积的百位上进1。
625431534127×11=
原来如此简单
6879746875397
你能找出下面每题中乘数的特点吗?
22 × 28 35 × 35 56 × 54
两个乘数十位上的数相同。
两个乘数个位上的数相加都等于10。
相同
2+8=10
相同
5+5=10
相同
6+4=10
观察比较
这几题的乘积会有什么特点?先算一算、 填一填, 再和同学交流。
22
× 28
176
44
616
35
× 35
175
105
1225
56
× 54
224
280
3024
22 × 28 35 × 35 56 × 54
=616
=1225
=3024
22 × 28 35 × 35 56 × 54
=616
=1225
=3024
2×(2+1)=6
2×8=16
3×(3+1)=12
5×5=25
5×(5+1)=30
6×4=24
建立猜想
观察:
(1)比较计算的结果,你有什么发现?
根据你的猜想直接写出下面得数, 再用计算验证。
15 × 15 = 43 × 47 = 69 × 61 =
验证猜想
24 × 26 = 44 × 46 = 74 × 76 =
25 × 25 = 45 × 45 = 75 × 75 =
624
625
25-1
25+1
625-1=624
2024
2025
45-1
45+1
2025-1=2024
5624
5625
75-1
75+1
5625-1=5624
发现:观察每组中的两道算式,你什么发现?
实践应用
24 × 26 = 44 × 46 = 74 × 76 =
25 × 25 = 45 × 45 = 75 × 75 =
624
625
25-1
25+1
625-1=624
2024
2025
45-1
45+1
2025-1=2024
5624
5625
75-1
75+1
5625-1=5624
1.每组中第二个算式的相同乘数相乘,第一个算式的两个乘数分别等于第二个算式的乘数减1、加1。
2.每组中第二个算式的积减1等于第一个算式的积。
实践应用
你能用更简洁的方式表示刚才发现的规律吗?
拓展延伸
(a-1) × (a+1)=a ×a
回顾探索和发现规律的过程,说说你的体会。
回顾总结
(1)可以通过仔细观察和比较发现规律。
(2)发现规律后,要通过计算进行验证。
(3)用发现的规律进行计算,能够算得又对又快。
有趣的乘法计算
苏教版三年级数学下册
吓人的算式
625431534127×11=
?
有规律
大事起于难,小事起于易,必作于细,必成于易。
——春秋时期《道德经》
你知道吗?
解决困难要从容易的地方入手
做成大事要从小事入手
24
24
264
53
53
583
24
× 11
53
×11
62
×11
62
62
682
简单的背后
笔算 24×11 53×11 62×11
24
× 11
24
24
264
53
×11
53
53
583
62
×11
62
62
682
观察比较
小组交流:
(1)得到的积与原来的哪个乘数有关?
(2)比较积的每一位数与这个乘数的每一位比较,你有什么发现?
24
× 11
24
24
264
53
×11
53
53
583
62
×11
62
62
682
积个位上的数,与原来两位数个位上的数一样。
建立猜想
发现一:
24
× 11
24
24
264
53
×11
53
53
583
62
×11
62
62
682
积百位上的数,与原来两位数十位上的数一样。
建立猜想
发现二:
24
× 11
24
24
264
53
×11
53
53
583
62
×11
62
62
682
6=2+4
8=5+3
8=6+2
积十位上的数, 等于原来两位数个位与十位上数的和。
建立猜想
发现三:
一个两位数与11相乘
积的个位上的数与原来两位数的个位上的数相同,
积的百位上的数与原来两位数的十位上的数相同,
积的十位上的数是原来两位数个位与十位上的数之和。
口诀记忆:两头一拉,中间相加;
我们的猜想
根据你的发现试着完成下面的填空, 再用竖式计算验证。
23 × 11 = 2 3
64 × 11 = 4
59 × 11 = 9
5
我们的猜想
23
× 11
23
23
253
验证:
根据你的发现试着完成下面的填空, 再用竖式计算验证。
23 × 11 = 2 3
64 × 11 = 4
59 × 11 = 9
5
当个位和十位上的数相加满10时, 该怎样做?
7
0
6
4
十位满十,百位加一。
6+4=10
5+9=14
我们的猜想
23 × 11 = 2 3
64 × 11 = 4
59 × 11 = 9
5
7
0
6
4
23
× 11
23
23
253
64
× 11
64
64
704
59
× 11
59
59
649
验证:
通过验证,发现我们的猜想是正确的。
一个两位数与11相乘:
积的个位上的数与原来两位数的个位上的数相同
积的百位上的数与原来两位数的十位上的数相同,
积的十位上的数是原来两位数个位与十位上的数之和。
口诀: 两头一拉,中间相加;
十位满十,百位加一。
我们的猜想
当两位数个位与十位上的数相加满10时,积的十位上写和的个位数字,向积的百位上进1。
625431534127×11=
原来如此简单
6879746875397
你能找出下面每题中乘数的特点吗?
22 × 28 35 × 35 56 × 54
两个乘数十位上的数相同。
两个乘数个位上的数相加都等于10。
相同
2+8=10
相同
5+5=10
相同
6+4=10
观察比较
这几题的乘积会有什么特点?先算一算、 填一填, 再和同学交流。
22
× 28
176
44
616
35
× 35
175
105
1225
56
× 54
224
280
3024
22 × 28 35 × 35 56 × 54
=616
=1225
=3024
22 × 28 35 × 35 56 × 54
=616
=1225
=3024
2×(2+1)=6
2×8=16
3×(3+1)=12
5×5=25
5×(5+1)=30
6×4=24
建立猜想
观察:
(1)比较计算的结果,你有什么发现?
根据你的猜想直接写出下面得数, 再用计算验证。
15 × 15 = 43 × 47 = 69 × 61 =
验证猜想
24 × 26 = 44 × 46 = 74 × 76 =
25 × 25 = 45 × 45 = 75 × 75 =
624
625
25-1
25+1
625-1=624
2024
2025
45-1
45+1
2025-1=2024
5624
5625
75-1
75+1
5625-1=5624
发现:观察每组中的两道算式,你什么发现?
实践应用
24 × 26 = 44 × 46 = 74 × 76 =
25 × 25 = 45 × 45 = 75 × 75 =
624
625
25-1
25+1
625-1=624
2024
2025
45-1
45+1
2025-1=2024
5624
5625
75-1
75+1
5625-1=5624
1.每组中第二个算式的相同乘数相乘,第一个算式的两个乘数分别等于第二个算式的乘数减1、加1。
2.每组中第二个算式的积减1等于第一个算式的积。
实践应用
你能用更简洁的方式表示刚才发现的规律吗?
拓展延伸
(a-1) × (a+1)=a ×a
回顾探索和发现规律的过程,说说你的体会。
回顾总结
(1)可以通过仔细观察和比较发现规律。
(2)发现规律后,要通过计算进行验证。
(3)用发现的规律进行计算,能够算得又对又快。
