2023-2024学年第二学期甘肃省武威第十六中学九年级数学开学学情评估(含答案)
文档属性
| 名称 | 2023-2024学年第二学期甘肃省武威第十六中学九年级数学开学学情评估(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 400.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-08 10:26:03 | ||
图片预览




文档简介
2023-2024学年第二学期甘肃省武威第十六中学九年级数学开学学情评估
一、选择题(共30分)
1.(3分)2023年10月12日,习近平总书记在进一步推动长江经济带高质量发展座谈会上强调:“要把产业绿色转型升级作为重中之重,加快培育壮大绿色低碳产业.”下列绿色图标中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(3分)若是一元二次方程的一个根,则q的值为( )
A. B.2 C. D.5
3.(3分)将抛物线向上平移3个单位,所得抛物线的解析式是( )
A. B. C. D.
4.(3分)如图,将绕点C旋转得到,点A对应点D,点B对应点E,点B刚好落在边上,,则( )
A. B. C. D.
5.(3分)初三毕业之际,在毕业晚会上同学们互赠照片以表留念,每人给其他同学送一张照片,一共送出110张照片,设晚会上有x人,则可列方程为( )
A. B.
C. D.
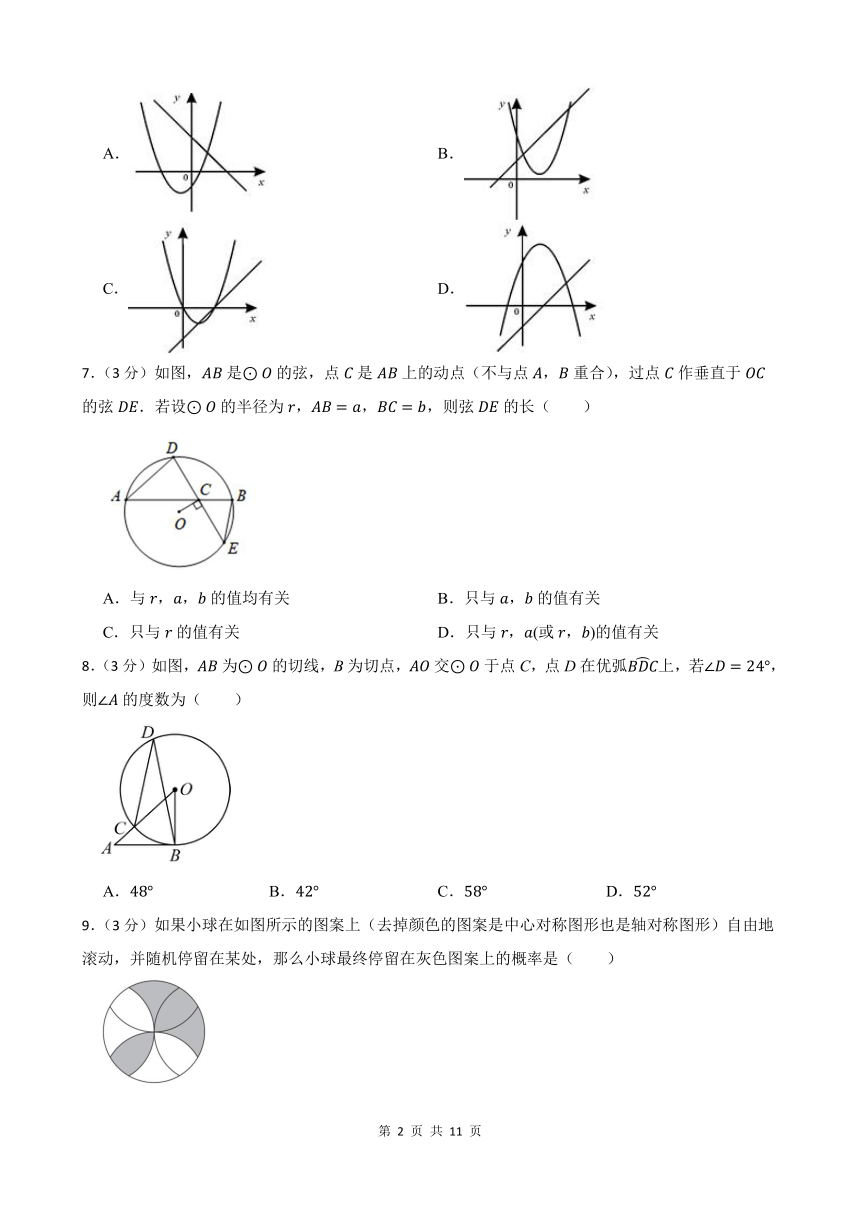
6.(3分)函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )
A. B.
C. D.
7.(3分)如图,是的弦,点是上的动点(不与点,重合),过点作垂直于的弦.若设的半径为,,,则弦的长( )
A.与,,的值均有关 B.只与,的值有关
C.只与的值有关 D.只与,(或,)的值有关
8.(3分)如图,为的切线,B为切点,交于点C,点D在优弧上,若,则的度数为( )
A. B. C. D.
9.(3分)如果小球在如图所示的图案上(去掉颜色的图案是中心对称图形也是轴对称图形)自由地滚动,并随机停留在某处,那么小球最终停留在灰色图案上的概率是( )
A. B. C. D.
10.(3分)如图,在圆形纸板上裁剪两个扇面具体操作如下:作的任意一条直径,以点为圆心、长为半径作圆,与相交于点、;以点为圆心、长为半径作圆,与相交于点、;连结、、、,得到两个扇形,并裁剪下来若的半径为,则剩余纸板图中阴影部分图形的面积为( )
A. B. C. D.
二、填空题(共24分)
11.(3分)已知一元二次方程有两个相等的实数根,则m的值为 .
12.(3分)已知 是一元二次方程 的一个根,则m的值为 ,方程的另一个根是
13.(3分)已知抛物线与关于原点成中心对称,若抛物线的解析式为,则抛物线的解析式为 .
14.(3分)将抛物线y=x2向下平移3个单位,再向右平移2个单位后,所得抛物线的解析式为 .
15.(3分)若点P(a,2)与点Q(5,b)关于原点对称,则a= ,b= .
16.(3分)如图,分别与相切于两点,且.若点是上异于点的一点,则的大小为 .
17.(3分)如图,四边形是的内接四边形,是的直径,,则的度数是 .
18.(3分)不透明的袋子中装有8个球,除颜色外无其他差别.每次把球充分搅匀后,随机摸出一个球记下颜色再放回袋子.通过大量重复试验,发现摸到白球的频率稳定于0.25,则袋子中白球的个数约是 .
三、解方程(共8分)
19.(1)(4分) (2)(4分)
四、作图题(共6分)
20.(6分)如图,在平面直角坐标中,已知,
(1)(2分)画出绕O点逆时针旋转后的图形,并写出的坐标.
(2)(2分)将(1)中所得先向左平移4个单位,再向上平移2个单位得到,画.
(3)(2分)若可看作绕某点旋转得来,则旋转中心的坐标为.
五、解答题(共52分)
21.(6分)等腰三角形三边的长分别为a,b,4,且a,b是关于x的一元二次方程x2-12x+k+2=0的两根,求k的值.
22.(6分)已知:如图,在中,,以为边向形外作等边三角形,把绕着点D按顺时针方向旋转后得到,且A、C、E三点共线,若,,求的度数与的长.
23.(6分)已知二次函数的图象经过A(-1,0),B(2,3)两点.
(1)(3分)求二次函数的表达式及顶点坐标.
(2)(3分)如果将此二次函数的图象向上平移n个单位后过点P(m,4),再将点P向右平移3个单位后得点Q,点Q恰好落在原二次函数+c的图象上,求n的值.
24.(8分)如图,是的直径,点C为外一点,过点 C作于点D,交于点F,连接 ,与相交于点A,点P为线段上一点,且
(1)(4分)求证:为的切线;
(2)(4分)若点F为的中点,的半径为5,,求的长.
25.(8分)如图,是的直径,是的一条弦,且于点E。
(1)(4分)求证:;
(2)(4分)若,,求阴影部分面积。
26.(8分)在一个不透明的盒子中放有三张卡片,分别标记为、、,每张卡片除了标记不同外,其余均相同.某同学第一次从盒子中随机抽取一张卡片,卡片放回,第二次又随机抽取一张卡片,请用画树状图(或列表)的方法,求两次抽取的卡片完全相同的概率.
27.(10分)如图,抛物线与x轴相交于两点,与y轴交于点C.
(1)(3分)求抛物线的解析式;
(2)(3分)抛物线的对称轴上是否存在一点M,使的周长值最小?若存在,请求出点M的坐标;若不存在,请说明理由.
(3)(4分)在抛物线上有一点P,过点P作x轴的垂线交x轴于点Q,若是等腰直角三角形,求点P的坐标.
答案
1-10 BDACC CBBCB
11.9 12.-1;2+ 13. 14.y=x2-4x+1 15.﹣5;﹣2 16.或
17.120 18.2
19.(1)解:
去括号合并同类项,,
对方程因式分解:,
故或,
解得:,
(2)解:
对方程因式分解:,
故或,
解得:,
20.(1)解:,的坐标为;
(2)解:
(3)解:如图,可以看作绕P点旋转得来,
作和的垂直平分线可以发现两者交于点
旋转中心P的坐标为.
21.∵a,b是关于x的一元二次方程x2-12x+h+2=0的两根,
∴b2- 4ac=(-12)2-4×1×(k+2)≥0,即k≤34.
∵等腰三角形三边的长分别为a,b,4,
∴当a=b时,有b2-4ac =(-12)2-4(k+2)= 0,解得k=34,
此时,方程的两根为x1=x2=6,即a=b=6,满足三角形的三边关系,符合题意;
当a=4时,有42-12×4+k+2=0,解得k=30.
当k=30时,方程的两根为x=4或x=8.
∴4+4=8,不满足三角形的三边关系,
∴k= 30不符合题意.
综上,k的值为34.
22.解:∵绕着点D按顺时针方向旋转后得到,
∴,,
∴为等边三角形,
∴,
∵点A、C、E在一条直线上,
∴,
∴,
∵绕着点D按顺时针方向旋转后得到,
∴,
∴,
∵为等边三角形,
∴.
23.(1)解:把 A(-1,0),B(2,3) 代入解析式得,解得,
∴二次函数解析式为,
,顶点坐标为.
(2)解: 将此二次函数的图象向上平移n个单位后,解析式为,过点 P(m,4),
∴,即,
点P向右平移3个单位后得点Q,点 代入,得,解得,
∴.
24.(1)证明:连接,,
∵是的直径,
∴,
∵,
∴,
∴,
∵,
∴,
∴
∵,
∴
∴,
∴
∴为的切线
(2)解:连接,
∵的半径为5,,
∴,,
∵,
∴,,
∵点F为的中点,
∴,
∴,
∴,
∴,
∴,
∴
25.(1)证明:∵,∴,
∵,∴,∴;
(2)解:∵是的直径,且于点E,∴,
∵,∴,
在Rt中,,
解得:(负数舍去),
26.解:
P(两次抽取的卡片完全相同)=.
27.(1)解:将分别代入,得
解得
所以抛物线的解析式为.
(2)解:存在.
因为点A,B关于对称轴对称,连接交对称轴于点M,此时的值最小,即的周长值最小.
令,得,所以.
设直线的函数解析式为.
将代入,得
解得
所以直线的函数解析式为.
因为抛物线的对称轴为,
当时,,
所以.
(3)解:因为轴于点Q,所以.
因为是等腰直角三角形,所以.
因为点P在抛物线上,所以设,则.
所以.
所以,即或.
整理,得或.
当时,解得或(舍去),此时;
当时,解得或(舍去),此时.
综上,点P的坐标为或
一、选择题(共30分)
1.(3分)2023年10月12日,习近平总书记在进一步推动长江经济带高质量发展座谈会上强调:“要把产业绿色转型升级作为重中之重,加快培育壮大绿色低碳产业.”下列绿色图标中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(3分)若是一元二次方程的一个根,则q的值为( )
A. B.2 C. D.5
3.(3分)将抛物线向上平移3个单位,所得抛物线的解析式是( )
A. B. C. D.
4.(3分)如图,将绕点C旋转得到,点A对应点D,点B对应点E,点B刚好落在边上,,则( )
A. B. C. D.
5.(3分)初三毕业之际,在毕业晚会上同学们互赠照片以表留念,每人给其他同学送一张照片,一共送出110张照片,设晚会上有x人,则可列方程为( )
A. B.
C. D.
6.(3分)函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )
A. B.
C. D.
7.(3分)如图,是的弦,点是上的动点(不与点,重合),过点作垂直于的弦.若设的半径为,,,则弦的长( )
A.与,,的值均有关 B.只与,的值有关
C.只与的值有关 D.只与,(或,)的值有关
8.(3分)如图,为的切线,B为切点,交于点C,点D在优弧上,若,则的度数为( )
A. B. C. D.
9.(3分)如果小球在如图所示的图案上(去掉颜色的图案是中心对称图形也是轴对称图形)自由地滚动,并随机停留在某处,那么小球最终停留在灰色图案上的概率是( )
A. B. C. D.
10.(3分)如图,在圆形纸板上裁剪两个扇面具体操作如下:作的任意一条直径,以点为圆心、长为半径作圆,与相交于点、;以点为圆心、长为半径作圆,与相交于点、;连结、、、,得到两个扇形,并裁剪下来若的半径为,则剩余纸板图中阴影部分图形的面积为( )
A. B. C. D.
二、填空题(共24分)
11.(3分)已知一元二次方程有两个相等的实数根,则m的值为 .
12.(3分)已知 是一元二次方程 的一个根,则m的值为 ,方程的另一个根是
13.(3分)已知抛物线与关于原点成中心对称,若抛物线的解析式为,则抛物线的解析式为 .
14.(3分)将抛物线y=x2向下平移3个单位,再向右平移2个单位后,所得抛物线的解析式为 .
15.(3分)若点P(a,2)与点Q(5,b)关于原点对称,则a= ,b= .
16.(3分)如图,分别与相切于两点,且.若点是上异于点的一点,则的大小为 .
17.(3分)如图,四边形是的内接四边形,是的直径,,则的度数是 .
18.(3分)不透明的袋子中装有8个球,除颜色外无其他差别.每次把球充分搅匀后,随机摸出一个球记下颜色再放回袋子.通过大量重复试验,发现摸到白球的频率稳定于0.25,则袋子中白球的个数约是 .
三、解方程(共8分)
19.(1)(4分) (2)(4分)
四、作图题(共6分)
20.(6分)如图,在平面直角坐标中,已知,
(1)(2分)画出绕O点逆时针旋转后的图形,并写出的坐标.
(2)(2分)将(1)中所得先向左平移4个单位,再向上平移2个单位得到,画.
(3)(2分)若可看作绕某点旋转得来,则旋转中心的坐标为.
五、解答题(共52分)
21.(6分)等腰三角形三边的长分别为a,b,4,且a,b是关于x的一元二次方程x2-12x+k+2=0的两根,求k的值.
22.(6分)已知:如图,在中,,以为边向形外作等边三角形,把绕着点D按顺时针方向旋转后得到,且A、C、E三点共线,若,,求的度数与的长.
23.(6分)已知二次函数的图象经过A(-1,0),B(2,3)两点.
(1)(3分)求二次函数的表达式及顶点坐标.
(2)(3分)如果将此二次函数的图象向上平移n个单位后过点P(m,4),再将点P向右平移3个单位后得点Q,点Q恰好落在原二次函数+c的图象上,求n的值.
24.(8分)如图,是的直径,点C为外一点,过点 C作于点D,交于点F,连接 ,与相交于点A,点P为线段上一点,且
(1)(4分)求证:为的切线;
(2)(4分)若点F为的中点,的半径为5,,求的长.
25.(8分)如图,是的直径,是的一条弦,且于点E。
(1)(4分)求证:;
(2)(4分)若,,求阴影部分面积。
26.(8分)在一个不透明的盒子中放有三张卡片,分别标记为、、,每张卡片除了标记不同外,其余均相同.某同学第一次从盒子中随机抽取一张卡片,卡片放回,第二次又随机抽取一张卡片,请用画树状图(或列表)的方法,求两次抽取的卡片完全相同的概率.
27.(10分)如图,抛物线与x轴相交于两点,与y轴交于点C.
(1)(3分)求抛物线的解析式;
(2)(3分)抛物线的对称轴上是否存在一点M,使的周长值最小?若存在,请求出点M的坐标;若不存在,请说明理由.
(3)(4分)在抛物线上有一点P,过点P作x轴的垂线交x轴于点Q,若是等腰直角三角形,求点P的坐标.
答案
1-10 BDACC CBBCB
11.9 12.-1;2+ 13. 14.y=x2-4x+1 15.﹣5;﹣2 16.或
17.120 18.2
19.(1)解:
去括号合并同类项,,
对方程因式分解:,
故或,
解得:,
(2)解:
对方程因式分解:,
故或,
解得:,
20.(1)解:,的坐标为;
(2)解:
(3)解:如图,可以看作绕P点旋转得来,
作和的垂直平分线可以发现两者交于点
旋转中心P的坐标为.
21.∵a,b是关于x的一元二次方程x2-12x+h+2=0的两根,
∴b2- 4ac=(-12)2-4×1×(k+2)≥0,即k≤34.
∵等腰三角形三边的长分别为a,b,4,
∴当a=b时,有b2-4ac =(-12)2-4(k+2)= 0,解得k=34,
此时,方程的两根为x1=x2=6,即a=b=6,满足三角形的三边关系,符合题意;
当a=4时,有42-12×4+k+2=0,解得k=30.
当k=30时,方程的两根为x=4或x=8.
∴4+4=8,不满足三角形的三边关系,
∴k= 30不符合题意.
综上,k的值为34.
22.解:∵绕着点D按顺时针方向旋转后得到,
∴,,
∴为等边三角形,
∴,
∵点A、C、E在一条直线上,
∴,
∴,
∵绕着点D按顺时针方向旋转后得到,
∴,
∴,
∵为等边三角形,
∴.
23.(1)解:把 A(-1,0),B(2,3) 代入解析式得,解得,
∴二次函数解析式为,
,顶点坐标为.
(2)解: 将此二次函数的图象向上平移n个单位后,解析式为,过点 P(m,4),
∴,即,
点P向右平移3个单位后得点Q,点 代入,得,解得,
∴.
24.(1)证明:连接,,
∵是的直径,
∴,
∵,
∴,
∴,
∵,
∴,
∴
∵,
∴
∴,
∴
∴为的切线
(2)解:连接,
∵的半径为5,,
∴,,
∵,
∴,,
∵点F为的中点,
∴,
∴,
∴,
∴,
∴,
∴
25.(1)证明:∵,∴,
∵,∴,∴;
(2)解:∵是的直径,且于点E,∴,
∵,∴,
在Rt中,,
解得:(负数舍去),
26.解:
P(两次抽取的卡片完全相同)=.
27.(1)解:将分别代入,得
解得
所以抛物线的解析式为.
(2)解:存在.
因为点A,B关于对称轴对称,连接交对称轴于点M,此时的值最小,即的周长值最小.
令,得,所以.
设直线的函数解析式为.
将代入,得
解得
所以直线的函数解析式为.
因为抛物线的对称轴为,
当时,,
所以.
(3)解:因为轴于点Q,所以.
因为是等腰直角三角形,所以.
因为点P在抛物线上,所以设,则.
所以.
所以,即或.
整理,得或.
当时,解得或(舍去),此时;
当时,解得或(舍去),此时.
综上,点P的坐标为或
同课章节目录
