山东省济宁市实验中学2023-2024学年高二下学期开学考试数学试卷(含解析)
文档属性
| 名称 | 山东省济宁市实验中学2023-2024学年高二下学期开学考试数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-08 23:32:04 | ||
图片预览




文档简介
山东省济宁市实验中学2023-2024学年高二下学期开学考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知直线l的方程为,则直线l的倾斜角为( )
A. B. C. D.
2.过点且与直线垂直的直线方程为( )
A. B.
C. D.
3.若直线与圆相离,则过点的直线与圆C的位置关系是( )
A.相离 B.相切 C.相交 D.不确定
4.已知在空间四边形ABCD中,,则( )
A. B. C. D.
5.数列满足,且,则的值为( )
A.2 B.1 C. D.-1
6.直线与x轴,y轴分别交于点A,B,以线段AB为直径的圆的方程为( )
A. B.
C. D.
7.甲 乙两队进行羽毛球决赛,现在的情形是甲队只要再赢一局就获得冠军,乙队需要再赢两局才能得到冠军,若甲队每局获胜的概率为,则甲队获得冠军的概率为( )
A. B. C. D.
8.观察下面数阵,
则该数阵中第9行,从左往右数的第20个数是( )
A.545 B.547 C.549 D.551
二、多项选择题
9.关于频率和概率,下列说法正确的是( )
A.某同学投篮3次,命中2次,则该同学每次投篮命中的概率为
B.费勒抛掷10000次硬币,得到硬币正面向上的频率为0.4979;皮尔逊抛掷24000次硬币,得到硬币正面向上的频率为0.5005.如果某同学抛掷36000次硬币那么得到硬币正面向上的频率可能大于0.5005
C.某类种子发芽的概率为0.903,若抽取2000粒种子试种,则一定会有1806粒种子发芽
D.将一颗质地均匀的骰子抛掷6000次,则掷出的点数大于2的次数大约为4000次
10.已知椭圆的两个焦点分别为,,与y轴正半轴交于点B,下列选项中给出的条件,能够求出椭圆E标准方程的选项是( )
A.,
B.已知椭圆E的离心率为,短轴长为2
C.是等边三角形,且椭圆E的离心率为
D.设椭圆E的焦距为4,点B在圆上
11.已知数列的前n项和为,且,则下列说法正确的是( )
A.数列的奇数项成等差数列 B.数列的偶数项成等比数列
C. D.
12.如图,若正方体的棱长为1,点M是正方体的侧面ADHE上的一个动点(含边界),P是棱上CG靠近G点的三等分点,则下列结论正确的有( )
A.沿正方体的表面从点A到点P的最短路程为
B.保持PM与BH垂直时,M的运动轨迹是线段
C.若保持,则点M在侧面ADHE内运动路径长度为
D.当M在D点时,三棱锥的体积取到最大值
三、填空题
13.已知向量,,满足,则___________.
14.在一段线路中并联两个自动控制的常用开关,只要其中有一个开关能够闭合,线路就能正常工作.假定在某段时间内每个开关能够闭合的概率都是0.7,则这段时间内线路正常工作的概率为_________________.
15.记为等比数列的前n项和.若,则______________.
16.已知椭圆,C的上顶点为A,两个焦点为,,离心率为.过且垂直于的直线与C交于D,E两点,的周长是13,则____________.
四、解答题
17.已知直线与垂直,且经过点.
(1)求的方程;
(2)若与圆相交于A,B两点,求.
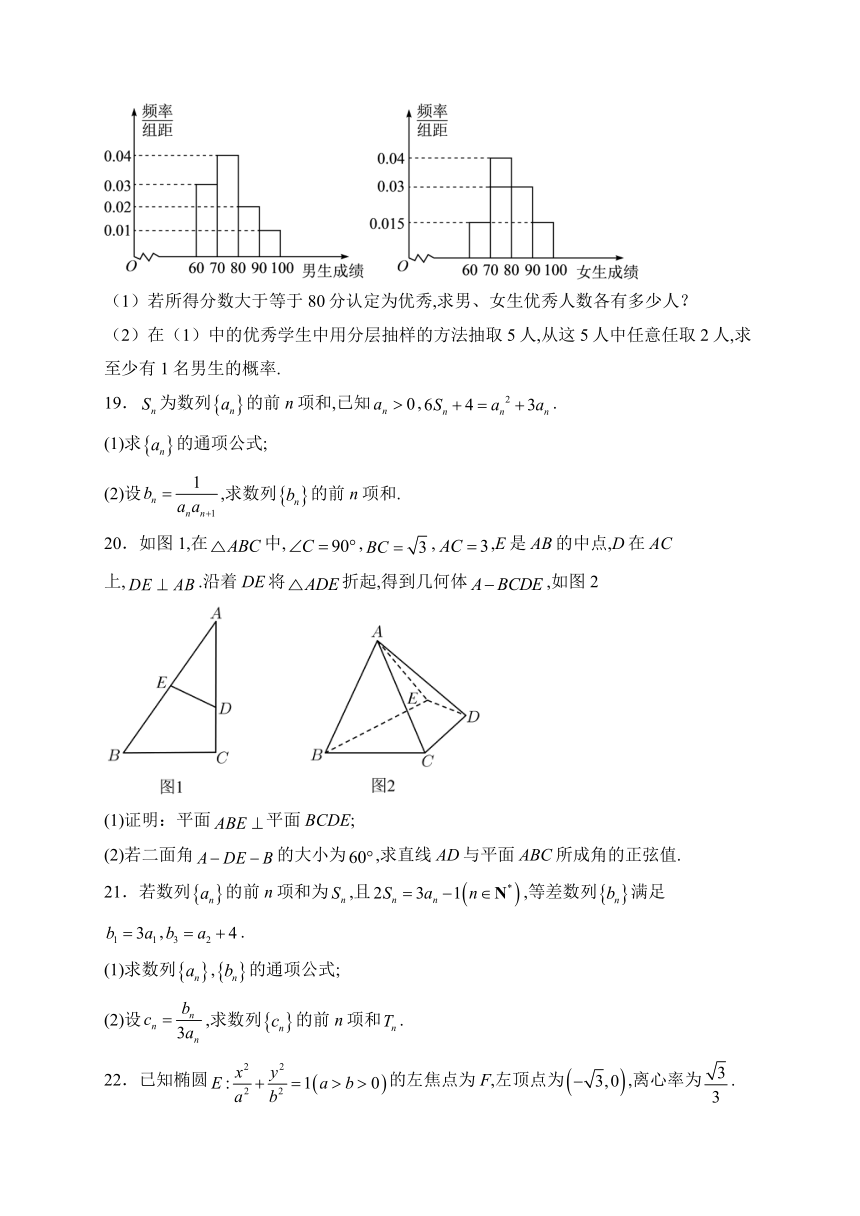
18.某校高二期中考试后,教务处计划对全年级数学成绩进行统计分析,从男、女生中各随机抽取100名学生,分别制成了男生和女生数学成绩的频率分布直方图,如图所示.
(1)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(2)在(1)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有1名男生的概率.
19.为数列的前n项和,已知,.
(1)求的通项公式;
(2)设,求数列的前n项和.
20.如图1,在中,,,,E是AB的中点,D在AC上,.沿着DE将折起,得到几何体,如图2
(1)证明:平面平面BCDE;
(2)若二面角的大小为,求直线AD与平面ABC所成角的正弦值.
21.若数列的前n项和为,且,等差数列满足,.
(1)求数列,的通项公式;
(2)设,求数列的前n项和.
22.已知椭圆的左焦点为F,左顶点为,离心率为.
(1)求E的方程;
(2)若过坐标原点O且斜率为的直线l与E交于A,B两点,直线AF与的另一个交点为C,的面积为,求直线AF的方程.
参考答案
1.答案:A
解析:由题意知,直线l的斜率为,
设直线l的倾斜角为,则,
解得,即直线l的倾斜角为.
故选:A.
2.答案:B
解析:直线的斜率为,
所以与直线垂直的直线斜率为,
故由点斜式可得,即,
故选:B.
3.答案:C
解析:因为直线与圆相离,
所以圆心到直线的距离大于半径,
即,所以,故点在圆内,
所以过点的直线与圆C相交,
故选:C.
4.答案:A
解析:因为,故G为CD的中点,如图,
由平行四边形法则可得,
所以.
故选:A.
5.答案:C
解析:因为数列满足,且,
可得,,,,···
可得数列是以2,,-1三项为周期的周期数列,
所以.
故选:C.
6.答案:B
解析:由题:,
法一:根据圆的直径式方程可以得到:
以线段AB为直径的圆的方程为,即,
故选:B.
法二:AB中点为(2,1),
故以线段AB为直径的圆的圆心为(2,1),半径为,
所以圆的方程为,展开化简得:,
故选:B.
7.答案:B
解析:由题意知:每局甲队获胜的概率为,乙队获胜的概率为,
至少在两局内甲队赢一局,甲队才能获得冠军,
当第一局甲队获胜,其概率为;
当第一局甲队输,第二局甲队赢,其概率为.
甲队获得冠军的概率为.
故选:B.
8.答案:C
解析:由题意可得该数阵中第m行有个数,
所以前m行共有个数,所以前8行共255个数.
因为该数阵中的数依次相连成等差数列,所以该数阵中第9行,
从左往右数的第20个数是.
故选:C.
9.答案:BD
解析:A中,某同学投篮3次,命中2次,只能说明频率为,而不能说明概率为,故A选项错误;
B中,当试验次数很多时,硬币正面向上的频率在0.5附近摆动,可能大于0.5,也可能小于0.5,故B选项正确;
C中,只能说明大约有1806粒种子发芽,并不是定有1806粒种子发芽,故C选项错误;
D中,点数大于2的概率为,故抛掷6000次点数大于2的次数大约为4000次,故D选项正确.
故选:BD.
10.答案:ABD
解析:根据之间的关系即可求解,故选项A正确;
根据,,即可求解,故选项B正确;
是等边三角形,且椭圆E的离心率为,只能确定,不能求椭圆E标准方程,故选项C不正确;
设椭圆的焦距为4,点B在圆上,
所以,
即可求出椭圆E标准方程,故选项D正确.
故选:ABD.
11.答案:BD
解析:,则,
两式相除得:,
中令得:,
因为,所以,
所以数列的奇数项成等比数列,首项为,公比为4,
数列的偶数项成等比数列,首项为,公比为4,
故A错误,B正确;
当n为奇数时,,
当n为偶数时,,
当n为奇数时,为偶数,故,
当n为偶数时,为奇数,故,
综上:,D正确;
,,C错误.
故选:BD.
12.答案:BD
解析:对于A,将正方体的下面和右面展开可得如下图形,
连接AP,则,
因此A到点P的最短路程为,故A错误;
对于B,建系如图,设,,,
,
所以,即,
又因为M是侧面ADHE上的一个动点(含边界),
所以M的运动轨迹是线段,
为DA靠近点D的三等分点和AE靠近点E三等分点的的连线段.
故B正确;
对于C,由B选项过程可得,
整理得,
所以M在侧面ADHE内运动路径是以为圆心,为半径的圆,
而点到的距离等于,
所以要保持,则点M在侧面ADHE外,
所以点M在侧面ADHE内运动路径长度为0,故C错误;
对于D,设平面BEP的法向量为,
,,
所以,令,解得,
所以点M到平面BEP的距离等于,
因为点M在平面ADHE内,所以,
所以当,,即当M在D点时,三棱锥的高最大,
又因为的面积为定值,
所以当M在D点时,三棱锥的体积最大,故D正确.
故选:BD.
13.答案:5
解析:因为,,,
所以, ,则,解得.
故答案为:5.
14.答案:0.91
解析:线路不能正常工作的概率为:,
能够正常工作的概率为,
故答案为:0.91.
15.答案:60
解析:设等比数列公比为q,
当时,,无解;
当时,,得,
.
故答案为:60.
16.答案:6
解析:如图,连接,,,
因为C的离心率为,所以,即,
所以,
因为,所以为等边三角形,
又,所以直线DE为线段的垂直平分线,
所以,,
则的周长为,
,
而,所以直线DE的方程为,
代入椭圆C的方程,得,
设,,则,,
所以,
故答案为:6.
17.答案:(1)
(2)8
解析:(1)由直线,可得斜率,
因为,所以直线的斜率为,
又因为直线过点,所以直线的方程为,
即.
(2)由圆,可得圆心,半径,
则圆心C到直线的距离为,
又由圆的弦长公式,可得弦长.
18.答案:(1)男30人,女45人
(2)
解析:(1)由题可得,男生优秀人数为人,
女生优秀人数为人;
(2)因为样本容量与总体中的个体数的比是,
所以样本中包含男生人数为人,女生人数为人.
设两名男生为,,三名女生为,,.
则从5人中任意选取2人构成的所有基本事件为:
,,,,,,,,,共10个,
记事件C:“选取的2人中至少有一名男生”,
则事件C包含的基本事件有:,,,,,,共7个.
所以.
19.答案:(1)
(2)
解析:(1)①当时,,
又, ,
②当时,由,可得
两式相减得:,整理得,
, ,
是以首项为4,公差为3的一个等差数列,
;
(2)由(1)可得,
数列的前n项和:.
20.答案:(1)证明见解析
(2)
解析:(1)证明:因为在图1中,沿着DE将折起,
所以在图2中有,,
又,
所以平面ABE,
又因为平面BCDE,
所以平面平面BCDE;
(2)由(1)知,,,
所以是二面角的平面角,
所以,
又因为,
所以是等边三角形,
连接CE,
在图1中,因为,,
所以,
因为E是AB的中点,
所以,
所以是等边三角形.
取BE的中点O,连接AO,CO,
则,,
因为平面平面BCDE,平面平面,
所以平面BCDE,
所以OB,OC,OA两两垂直,
以O为原点,,,为x,y,z轴建系,如图所示.
,,,
所以,,
设平面ABC的法向量为,
则即
取,得平面ABC的一个法向量为,
所以.
设直线AD与平面ABC所成角为,则.
21.答案:(1);
(2)
解析:(1),
又,
两式相减得,
即,故数列是以3为公比的等比数列,
又当时,,得,
,
,,
等差数列的公差为,
(2)由(1)可得,
,
上两式相减得,
22.答案:(1)
(2)或
解析:(1)设椭圆E的半焦距为.
因为椭圆E的左顶点为,所以.
又离心率,所以.
所以,
所以E的方程为.
(2)由(1)可知,设直线AF的方程为.
由消去x并整理得.
设,,
则,,
所以.
因此,
解得,即,
所以直线AF的方程为或.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知直线l的方程为,则直线l的倾斜角为( )
A. B. C. D.
2.过点且与直线垂直的直线方程为( )
A. B.
C. D.
3.若直线与圆相离,则过点的直线与圆C的位置关系是( )
A.相离 B.相切 C.相交 D.不确定
4.已知在空间四边形ABCD中,,则( )
A. B. C. D.
5.数列满足,且,则的值为( )
A.2 B.1 C. D.-1
6.直线与x轴,y轴分别交于点A,B,以线段AB为直径的圆的方程为( )
A. B.
C. D.
7.甲 乙两队进行羽毛球决赛,现在的情形是甲队只要再赢一局就获得冠军,乙队需要再赢两局才能得到冠军,若甲队每局获胜的概率为,则甲队获得冠军的概率为( )
A. B. C. D.
8.观察下面数阵,
则该数阵中第9行,从左往右数的第20个数是( )
A.545 B.547 C.549 D.551
二、多项选择题
9.关于频率和概率,下列说法正确的是( )
A.某同学投篮3次,命中2次,则该同学每次投篮命中的概率为
B.费勒抛掷10000次硬币,得到硬币正面向上的频率为0.4979;皮尔逊抛掷24000次硬币,得到硬币正面向上的频率为0.5005.如果某同学抛掷36000次硬币那么得到硬币正面向上的频率可能大于0.5005
C.某类种子发芽的概率为0.903,若抽取2000粒种子试种,则一定会有1806粒种子发芽
D.将一颗质地均匀的骰子抛掷6000次,则掷出的点数大于2的次数大约为4000次
10.已知椭圆的两个焦点分别为,,与y轴正半轴交于点B,下列选项中给出的条件,能够求出椭圆E标准方程的选项是( )
A.,
B.已知椭圆E的离心率为,短轴长为2
C.是等边三角形,且椭圆E的离心率为
D.设椭圆E的焦距为4,点B在圆上
11.已知数列的前n项和为,且,则下列说法正确的是( )
A.数列的奇数项成等差数列 B.数列的偶数项成等比数列
C. D.
12.如图,若正方体的棱长为1,点M是正方体的侧面ADHE上的一个动点(含边界),P是棱上CG靠近G点的三等分点,则下列结论正确的有( )
A.沿正方体的表面从点A到点P的最短路程为
B.保持PM与BH垂直时,M的运动轨迹是线段
C.若保持,则点M在侧面ADHE内运动路径长度为
D.当M在D点时,三棱锥的体积取到最大值
三、填空题
13.已知向量,,满足,则___________.
14.在一段线路中并联两个自动控制的常用开关,只要其中有一个开关能够闭合,线路就能正常工作.假定在某段时间内每个开关能够闭合的概率都是0.7,则这段时间内线路正常工作的概率为_________________.
15.记为等比数列的前n项和.若,则______________.
16.已知椭圆,C的上顶点为A,两个焦点为,,离心率为.过且垂直于的直线与C交于D,E两点,的周长是13,则____________.
四、解答题
17.已知直线与垂直,且经过点.
(1)求的方程;
(2)若与圆相交于A,B两点,求.
18.某校高二期中考试后,教务处计划对全年级数学成绩进行统计分析,从男、女生中各随机抽取100名学生,分别制成了男生和女生数学成绩的频率分布直方图,如图所示.
(1)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(2)在(1)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有1名男生的概率.
19.为数列的前n项和,已知,.
(1)求的通项公式;
(2)设,求数列的前n项和.
20.如图1,在中,,,,E是AB的中点,D在AC上,.沿着DE将折起,得到几何体,如图2
(1)证明:平面平面BCDE;
(2)若二面角的大小为,求直线AD与平面ABC所成角的正弦值.
21.若数列的前n项和为,且,等差数列满足,.
(1)求数列,的通项公式;
(2)设,求数列的前n项和.
22.已知椭圆的左焦点为F,左顶点为,离心率为.
(1)求E的方程;
(2)若过坐标原点O且斜率为的直线l与E交于A,B两点,直线AF与的另一个交点为C,的面积为,求直线AF的方程.
参考答案
1.答案:A
解析:由题意知,直线l的斜率为,
设直线l的倾斜角为,则,
解得,即直线l的倾斜角为.
故选:A.
2.答案:B
解析:直线的斜率为,
所以与直线垂直的直线斜率为,
故由点斜式可得,即,
故选:B.
3.答案:C
解析:因为直线与圆相离,
所以圆心到直线的距离大于半径,
即,所以,故点在圆内,
所以过点的直线与圆C相交,
故选:C.
4.答案:A
解析:因为,故G为CD的中点,如图,
由平行四边形法则可得,
所以.
故选:A.
5.答案:C
解析:因为数列满足,且,
可得,,,,···
可得数列是以2,,-1三项为周期的周期数列,
所以.
故选:C.
6.答案:B
解析:由题:,
法一:根据圆的直径式方程可以得到:
以线段AB为直径的圆的方程为,即,
故选:B.
法二:AB中点为(2,1),
故以线段AB为直径的圆的圆心为(2,1),半径为,
所以圆的方程为,展开化简得:,
故选:B.
7.答案:B
解析:由题意知:每局甲队获胜的概率为,乙队获胜的概率为,
至少在两局内甲队赢一局,甲队才能获得冠军,
当第一局甲队获胜,其概率为;
当第一局甲队输,第二局甲队赢,其概率为.
甲队获得冠军的概率为.
故选:B.
8.答案:C
解析:由题意可得该数阵中第m行有个数,
所以前m行共有个数,所以前8行共255个数.
因为该数阵中的数依次相连成等差数列,所以该数阵中第9行,
从左往右数的第20个数是.
故选:C.
9.答案:BD
解析:A中,某同学投篮3次,命中2次,只能说明频率为,而不能说明概率为,故A选项错误;
B中,当试验次数很多时,硬币正面向上的频率在0.5附近摆动,可能大于0.5,也可能小于0.5,故B选项正确;
C中,只能说明大约有1806粒种子发芽,并不是定有1806粒种子发芽,故C选项错误;
D中,点数大于2的概率为,故抛掷6000次点数大于2的次数大约为4000次,故D选项正确.
故选:BD.
10.答案:ABD
解析:根据之间的关系即可求解,故选项A正确;
根据,,即可求解,故选项B正确;
是等边三角形,且椭圆E的离心率为,只能确定,不能求椭圆E标准方程,故选项C不正确;
设椭圆的焦距为4,点B在圆上,
所以,
即可求出椭圆E标准方程,故选项D正确.
故选:ABD.
11.答案:BD
解析:,则,
两式相除得:,
中令得:,
因为,所以,
所以数列的奇数项成等比数列,首项为,公比为4,
数列的偶数项成等比数列,首项为,公比为4,
故A错误,B正确;
当n为奇数时,,
当n为偶数时,,
当n为奇数时,为偶数,故,
当n为偶数时,为奇数,故,
综上:,D正确;
,,C错误.
故选:BD.
12.答案:BD
解析:对于A,将正方体的下面和右面展开可得如下图形,
连接AP,则,
因此A到点P的最短路程为,故A错误;
对于B,建系如图,设,,,
,
所以,即,
又因为M是侧面ADHE上的一个动点(含边界),
所以M的运动轨迹是线段,
为DA靠近点D的三等分点和AE靠近点E三等分点的的连线段.
故B正确;
对于C,由B选项过程可得,
整理得,
所以M在侧面ADHE内运动路径是以为圆心,为半径的圆,
而点到的距离等于,
所以要保持,则点M在侧面ADHE外,
所以点M在侧面ADHE内运动路径长度为0,故C错误;
对于D,设平面BEP的法向量为,
,,
所以,令,解得,
所以点M到平面BEP的距离等于,
因为点M在平面ADHE内,所以,
所以当,,即当M在D点时,三棱锥的高最大,
又因为的面积为定值,
所以当M在D点时,三棱锥的体积最大,故D正确.
故选:BD.
13.答案:5
解析:因为,,,
所以, ,则,解得.
故答案为:5.
14.答案:0.91
解析:线路不能正常工作的概率为:,
能够正常工作的概率为,
故答案为:0.91.
15.答案:60
解析:设等比数列公比为q,
当时,,无解;
当时,,得,
.
故答案为:60.
16.答案:6
解析:如图,连接,,,
因为C的离心率为,所以,即,
所以,
因为,所以为等边三角形,
又,所以直线DE为线段的垂直平分线,
所以,,
则的周长为,
,
而,所以直线DE的方程为,
代入椭圆C的方程,得,
设,,则,,
所以,
故答案为:6.
17.答案:(1)
(2)8
解析:(1)由直线,可得斜率,
因为,所以直线的斜率为,
又因为直线过点,所以直线的方程为,
即.
(2)由圆,可得圆心,半径,
则圆心C到直线的距离为,
又由圆的弦长公式,可得弦长.
18.答案:(1)男30人,女45人
(2)
解析:(1)由题可得,男生优秀人数为人,
女生优秀人数为人;
(2)因为样本容量与总体中的个体数的比是,
所以样本中包含男生人数为人,女生人数为人.
设两名男生为,,三名女生为,,.
则从5人中任意选取2人构成的所有基本事件为:
,,,,,,,,,共10个,
记事件C:“选取的2人中至少有一名男生”,
则事件C包含的基本事件有:,,,,,,共7个.
所以.
19.答案:(1)
(2)
解析:(1)①当时,,
又, ,
②当时,由,可得
两式相减得:,整理得,
, ,
是以首项为4,公差为3的一个等差数列,
;
(2)由(1)可得,
数列的前n项和:.
20.答案:(1)证明见解析
(2)
解析:(1)证明:因为在图1中,沿着DE将折起,
所以在图2中有,,
又,
所以平面ABE,
又因为平面BCDE,
所以平面平面BCDE;
(2)由(1)知,,,
所以是二面角的平面角,
所以,
又因为,
所以是等边三角形,
连接CE,
在图1中,因为,,
所以,
因为E是AB的中点,
所以,
所以是等边三角形.
取BE的中点O,连接AO,CO,
则,,
因为平面平面BCDE,平面平面,
所以平面BCDE,
所以OB,OC,OA两两垂直,
以O为原点,,,为x,y,z轴建系,如图所示.
,,,
所以,,
设平面ABC的法向量为,
则即
取,得平面ABC的一个法向量为,
所以.
设直线AD与平面ABC所成角为,则.
21.答案:(1);
(2)
解析:(1),
又,
两式相减得,
即,故数列是以3为公比的等比数列,
又当时,,得,
,
,,
等差数列的公差为,
(2)由(1)可得,
,
上两式相减得,
22.答案:(1)
(2)或
解析:(1)设椭圆E的半焦距为.
因为椭圆E的左顶点为,所以.
又离心率,所以.
所以,
所以E的方程为.
(2)由(1)可知,设直线AF的方程为.
由消去x并整理得.
设,,
则,,
所以.
因此,
解得,即,
所以直线AF的方程为或.
同课章节目录
