黑龙江省哈尔滨市呼兰区2023-2024学年九年级下学期开学考试数学试题(含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市呼兰区2023-2024学年九年级下学期开学考试数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-08 19:42:21 | ||
图片预览


文档简介
2023-2024下学期九年级期初质量测查
数学试卷
考生须知:
1、本试卷满分为120分,考试时间为120分钟.
2、答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确粘贴在条形码区域内.
3、请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效.
4、选择题必须使用2B铅笔填涂:非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.
5、保持卡面整洁,不要折叠、不要弄脏、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷 选择题(共30分)(涂卡)
一、选择题(每题3分,计30分,每题只有一个正确的答案)
1.2024的相反数是( )
A. B.2024 C. D.
2.下列计算中正确的是( )
A. B. C. D.
3.各学科的图形都蕴含着对称美,下列图形中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.国家级非物质文化遗产之一的东北大鼓是中国北方曲种,流行于辽宁、吉林、黑龙江3省,如图是表演情景及乐器之一鼓的立体图形,该立体图形的主视图是( )
A. B. C. D.
5.已知点在双曲线的图象上,则下列各点也在该双曲线上的是( )
A. B. C. D.
6.分式方程的解是( )
A. B. C. D.
7.第三届“一带一路”国际高峰论坛在北京成功召开,大会回顾了10年来共建“一带一路”取得的丰硕成果,根据有关数据统计显示,2020年中欧贸易总额约为5800亿欧元,2022年中欧贸易总额约为8600亿欧元,设这两年中欧贸易总额的年平均增长率为x,则可列方程为( )
A. B.
C. D.
8.将抛物线的图象向右平移2个单位,再向下平移6个单位,平移后所得抛物线的解析式为( )
A. B. C. D.
9.如图是某景区大门部分建筑,已知,当时,则AB的长是( ),
A. B. C. D.
10.图中反映某网约车平台收费y(元)与所行驶的路程x(千米)的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费64元,若车速始终保持60千米/时不变,不考虑其它因素(红绿灯、堵车等),他从家到机场需要( )
A.10分钟 B.15分钟 C.18分钟 D.20分钟
第Ⅱ卷 非选择题(共90分)
二、填空题(每小题3分,共计30分)
11.本届哈尔滨冰雪大世界面积超810000平方米,是世界上最大的冰雪主题乐园,荣获一项新的吉尼斯世界纪录称号.数字810000用科学记数法表示为________.
12.函数中,自变量x的取值范围是_________.
13.把多项式分解因式的结果是__________.
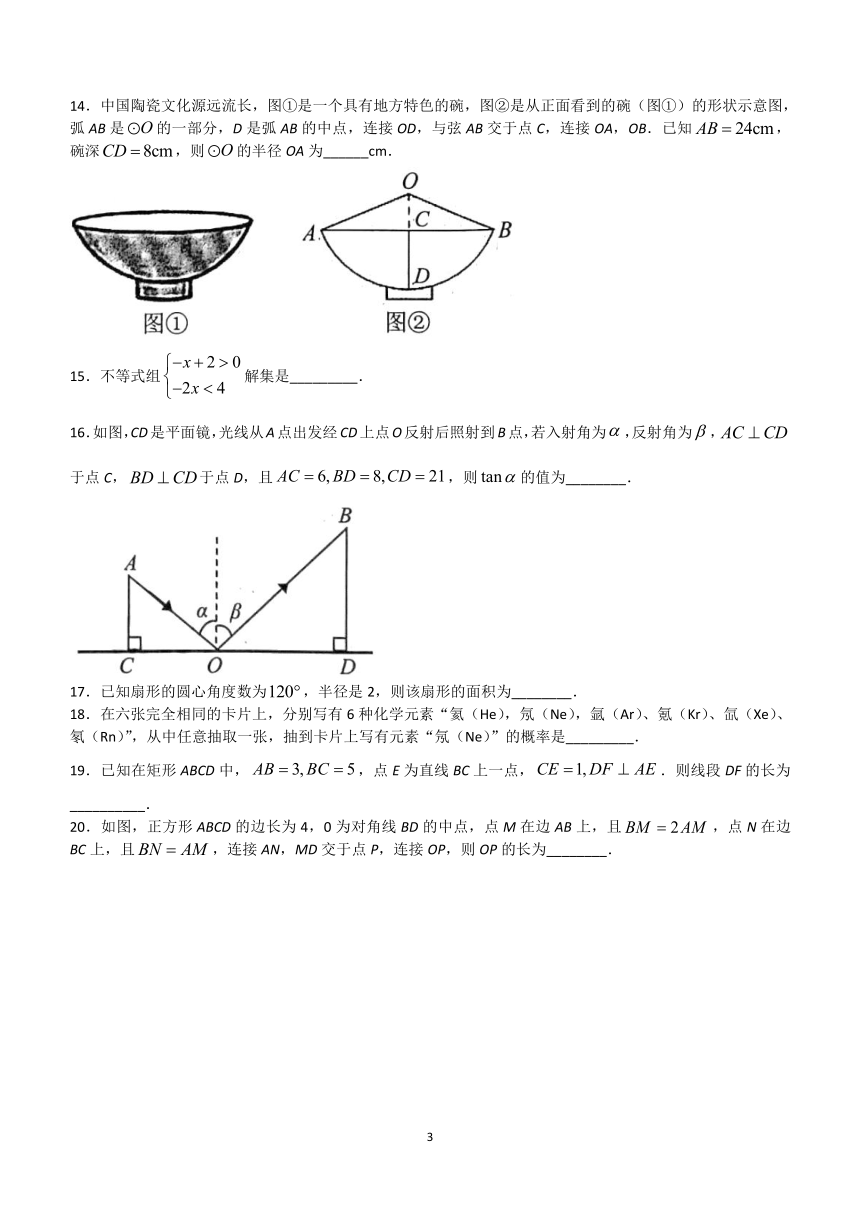
14.中国陶瓷文化源远流长,图①是一个具有地方特色的碗,图②是从正面看到的碗(图①)的形状示意图,弧AB是的一部分,D是弧AB的中点,连接OD,与弦AB交于点C,连接OA,OB.已知,碗深,则的半径OA为______cm.
15.不等式组解集是_________.
16.如图,CD是平面镜,光线从A点出发经CD上点O反射后照射到B点,若入射角为,反射角为,于点C,于点D,且,则的值为________.
17.已知扇形的圆心角度数为,半径是2,则该扇形的面积为________.
18.在六张完全相同的卡片上,分别写有6种化学元素“氦(He),氖(Ne),氩(Ar)、氪(Kr)、氙(Xe)、氡(Rn)”,从中任意抽取一张,抽到卡片上写有元素“氖(Ne)”的概率是_________.
19.已知在矩形ABCD中,,点E为直线BC上一点,.则线段DF的长为__________.
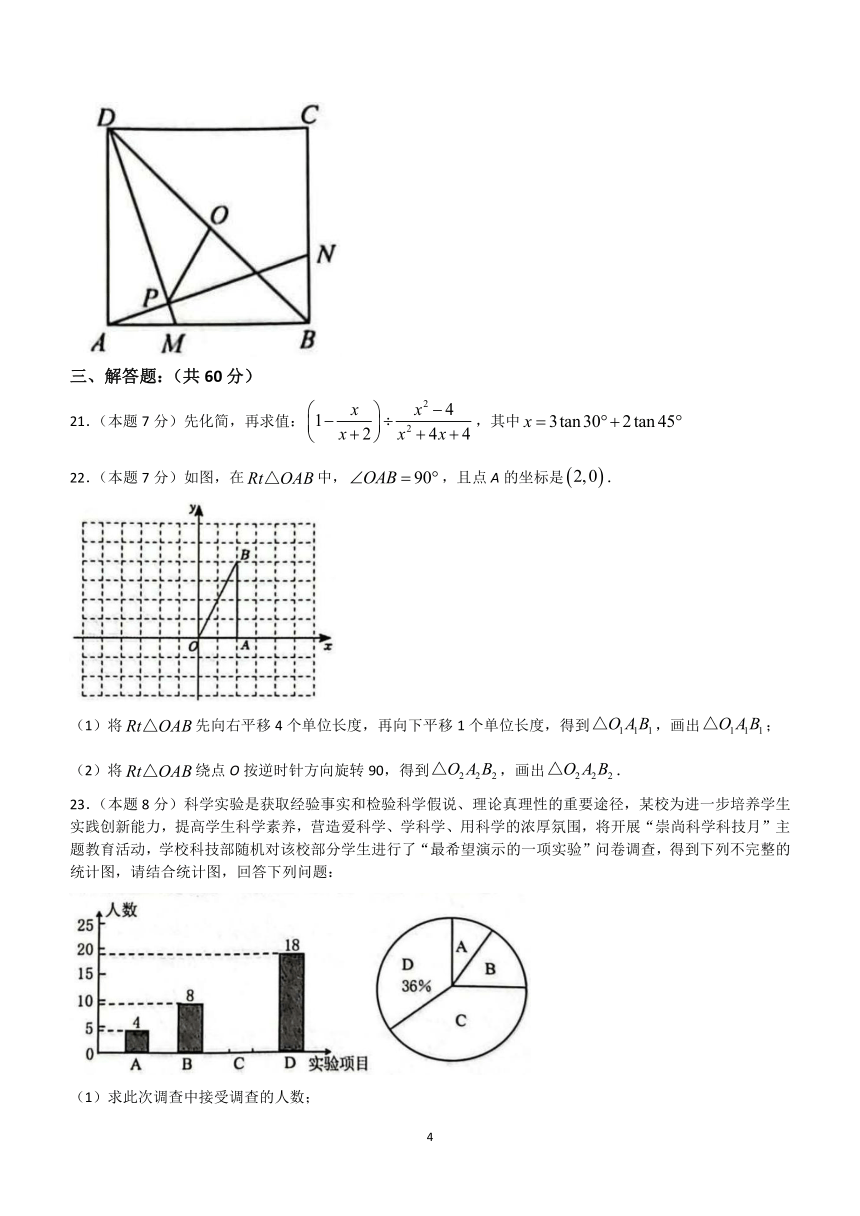
20.如图,正方形ABCD的边长为4,0为对角线BD的中点,点M在边AB上,且,点N在边BC上,且,连接AN,MD交于点P,连接OP,则OP的长为________.
三、解答题:(共60分)
21.(本题7分)先化简,再求值:,其中
22.(本题7分)如图,在中,,且点A的坐标是.
(1)将先向右平移4个单位长度,再向下平移1个单位长度,得到,画出;
(2)将绕点O按逆时针方向旋转90,得到,画出.
23.(本题8分)科学实验是获取经验事实和检验科学假说、理论真理性的重要途径,某校为进一步培养学生实践创新能力,提高学生科学素养,营造爱科学、学科学、用科学的浓厚氛围,将开展“崇尚科学科技月”主题教育活动,学校科技部随机对该校部分学生进行了“最希望演示的一项实验”问卷调查,得到下列不完整的统计图,请结合统计图,回答下列问题:
(1)求此次调查中接受调查的人数;
(2)通过计算,请补全条形统计图;
(3)如果这所学校有1500名学生,请估计该校最希望演示B项实验的学生有多少人
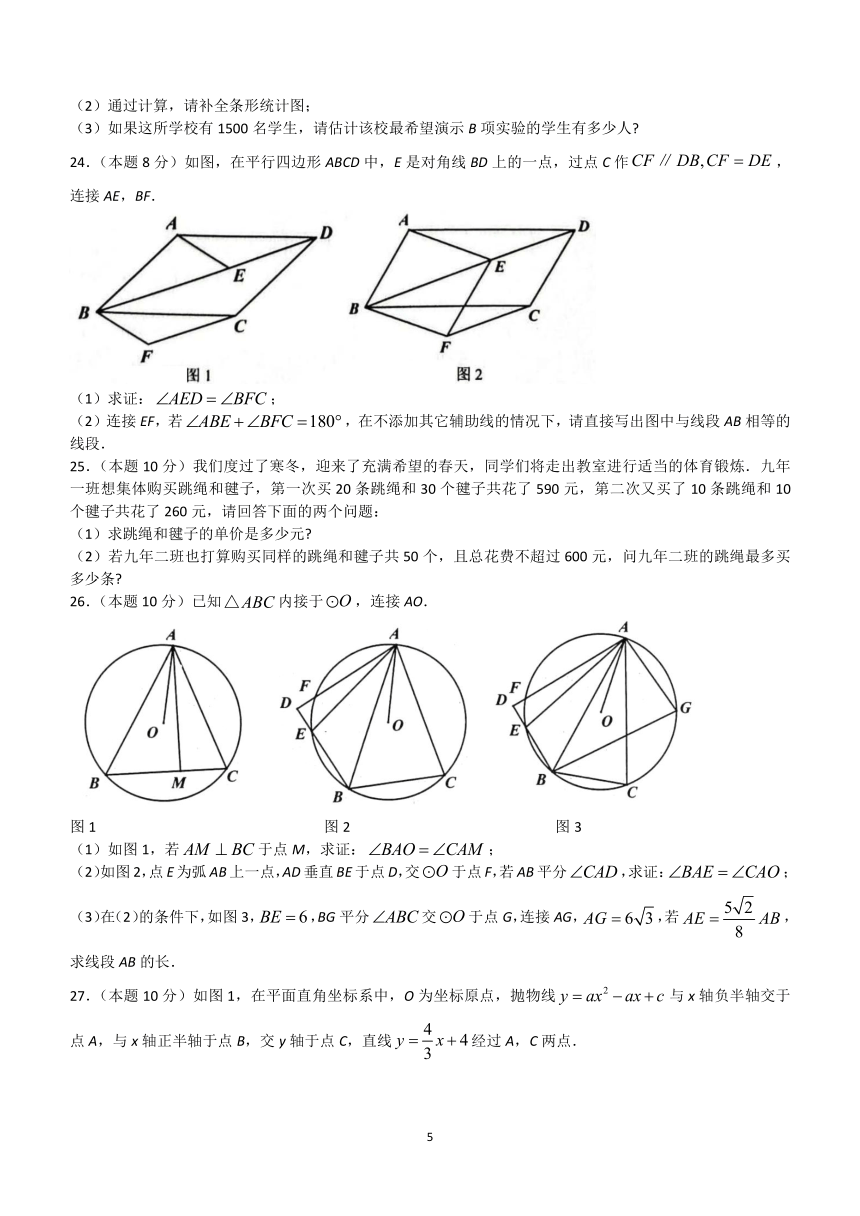
24.(本题8分)如图,在平行四边形ABCD中,E是对角线BD上的一点,过点C作,连接AE,BF.
(1)求证:;
(2)连接EF,若,在不添加其它辅助线的情况下,请直接写出图中与线段AB相等的线段.
25.(本题10分)我们度过了寒冬,迎来了充满希望的春天,同学们将走出教室进行适当的体育锻炼.九年一班想集体购买跳绳和毽子,第一次买20条跳绳和30个毽子共花了590元,第二次又买了10条跳绳和10个毽子共花了260元,请回答下面的两个问题:
(1)求跳绳和毽子的单价是多少元
(2)若九年二班也打算购买同样的跳绳和毽子共50个,且总花费不超过600元,问九年二班的跳绳最多买多少条
26.(本题10分)已知内接于,连接AO.
图1 图2 图3
(1)如图1,若于点M,求证:;
(2)如图2,点E为弧AB上一点,AD垂直BE于点D,交于点F,若AB平分,求证:;
(3)在(2)的条件下,如图3,,BG平分交于点G,连接AG,,若,求线段AB的长.
27.(本题10分)如图1,在平面直角坐标系中,O为坐标原点,抛物线与x轴负半轴交于点A,与x轴正半轴于点B,交y轴于点C,直线经过A,C两点.
图1 图2 图3
(1)求抛物线的解析式;
(2)如图2,点P为第一象限抛物线上一点,交y轴于点D,若设线段PD的长为d,点P的横坐标为t,求d与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,连接AD,点E为抛物线上第四象限上一点,,连接CE交x轴于点F,若,求点P的横坐标.
2023-2024学年度下学期九年级模拟考试题
数学试卷参考答案
一、1-5.ACCBC 6-10.ABADD
二、11. 12. 13. 14.13 15.
16. 17. 18. 19.3或 20.
三、21.解:原式
当
∴原式
22.(1)画图正确
(2)画图正确
23.解:(1)(人) 1'
答:此次调查中接受调查的人数是50人 1'
(2)最希望演示C实验的人数为 (人) 2' 补图略 .1'
(3) (人) 2'
答:估计该校最希望演示B项实验的学生有240人. 1'
24.解︰(1)∵四边形ABCD是平行四边形∴,∴. 1'
∵,∴,∴ 1'
∵,∴ 1'
∴ 1'
(2)AE、BF、EF、CD(每个1,共4分)
25.2 (1)解:设跳绳的单价为x元,毽子的单价为y元.
根据题意得: 2'
解得: 2'
答:跳绳的单价为19元,毽子的单价为7元. 1'
(2)设九年二班购买a条跳绳,则购买个毽子.
根据题意得: 2'
解得: 1'
∵a为正整数
∴a的最大值为20.
答:九年二班的跳绳最多买20条
26.(1)证明:连接OB,∴,∵,
∴,∴ 1'
∵,∴,
∴,∴ 1'
(2)连接AO,BO,∴,∵,
∴,∴,
∵,∴. 1'
∵,∴,
∴,∴ .1'
∴AB平分,
∴,∴ 1'
(3)连接OE,OB,延长AO交于点N,连接OC,CN
∵
∴,∴ 1'
∵BG平分,∴
连接OG交AC于点K
∵
∴,
∵
∴OG垂直平分AC,∵
∴. 1'
在和中
∴,解得 1'
∴
∴
过点E作于点T
∴ 1'
∵,∴,
∴. 1'
27.解:(1)∵直线经过A,C两点
∴当时,;当时,
∴ 1'
把代入得,解得
∴抛物线的解析式为 1'
(2)∵,∴
∴ 1'
过点Р作轴于点K,∴
∵,∴,
∴,∴ 2'
(3)过点D作交CA延长线于点M,于点N,
∴
∵四边形ADEC的内角和为,,
∴,∵,
∴ 1'
∵,∴, 1'
∴CD平分,∵,∴
∴,∴
设直线CF的解析式为,∴,解得
∴直线CF的解析式为. 1'
联立与组成方程组得
得,∴ 1'
设点,
过点E作于点Q,∴
∴
∴,解得 1'
∴
∴
解得
∴点P的横坐标是 1
数学试卷
考生须知:
1、本试卷满分为120分,考试时间为120分钟.
2、答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确粘贴在条形码区域内.
3、请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题纸上答题无效.
4、选择题必须使用2B铅笔填涂:非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.
5、保持卡面整洁,不要折叠、不要弄脏、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷 选择题(共30分)(涂卡)
一、选择题(每题3分,计30分,每题只有一个正确的答案)
1.2024的相反数是( )
A. B.2024 C. D.
2.下列计算中正确的是( )
A. B. C. D.
3.各学科的图形都蕴含着对称美,下列图形中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.国家级非物质文化遗产之一的东北大鼓是中国北方曲种,流行于辽宁、吉林、黑龙江3省,如图是表演情景及乐器之一鼓的立体图形,该立体图形的主视图是( )
A. B. C. D.
5.已知点在双曲线的图象上,则下列各点也在该双曲线上的是( )
A. B. C. D.
6.分式方程的解是( )
A. B. C. D.
7.第三届“一带一路”国际高峰论坛在北京成功召开,大会回顾了10年来共建“一带一路”取得的丰硕成果,根据有关数据统计显示,2020年中欧贸易总额约为5800亿欧元,2022年中欧贸易总额约为8600亿欧元,设这两年中欧贸易总额的年平均增长率为x,则可列方程为( )
A. B.
C. D.
8.将抛物线的图象向右平移2个单位,再向下平移6个单位,平移后所得抛物线的解析式为( )
A. B. C. D.
9.如图是某景区大门部分建筑,已知,当时,则AB的长是( ),
A. B. C. D.
10.图中反映某网约车平台收费y(元)与所行驶的路程x(千米)的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费64元,若车速始终保持60千米/时不变,不考虑其它因素(红绿灯、堵车等),他从家到机场需要( )
A.10分钟 B.15分钟 C.18分钟 D.20分钟
第Ⅱ卷 非选择题(共90分)
二、填空题(每小题3分,共计30分)
11.本届哈尔滨冰雪大世界面积超810000平方米,是世界上最大的冰雪主题乐园,荣获一项新的吉尼斯世界纪录称号.数字810000用科学记数法表示为________.
12.函数中,自变量x的取值范围是_________.
13.把多项式分解因式的结果是__________.
14.中国陶瓷文化源远流长,图①是一个具有地方特色的碗,图②是从正面看到的碗(图①)的形状示意图,弧AB是的一部分,D是弧AB的中点,连接OD,与弦AB交于点C,连接OA,OB.已知,碗深,则的半径OA为______cm.
15.不等式组解集是_________.
16.如图,CD是平面镜,光线从A点出发经CD上点O反射后照射到B点,若入射角为,反射角为,于点C,于点D,且,则的值为________.
17.已知扇形的圆心角度数为,半径是2,则该扇形的面积为________.
18.在六张完全相同的卡片上,分别写有6种化学元素“氦(He),氖(Ne),氩(Ar)、氪(Kr)、氙(Xe)、氡(Rn)”,从中任意抽取一张,抽到卡片上写有元素“氖(Ne)”的概率是_________.
19.已知在矩形ABCD中,,点E为直线BC上一点,.则线段DF的长为__________.
20.如图,正方形ABCD的边长为4,0为对角线BD的中点,点M在边AB上,且,点N在边BC上,且,连接AN,MD交于点P,连接OP,则OP的长为________.
三、解答题:(共60分)
21.(本题7分)先化简,再求值:,其中
22.(本题7分)如图,在中,,且点A的坐标是.
(1)将先向右平移4个单位长度,再向下平移1个单位长度,得到,画出;
(2)将绕点O按逆时针方向旋转90,得到,画出.
23.(本题8分)科学实验是获取经验事实和检验科学假说、理论真理性的重要途径,某校为进一步培养学生实践创新能力,提高学生科学素养,营造爱科学、学科学、用科学的浓厚氛围,将开展“崇尚科学科技月”主题教育活动,学校科技部随机对该校部分学生进行了“最希望演示的一项实验”问卷调查,得到下列不完整的统计图,请结合统计图,回答下列问题:
(1)求此次调查中接受调查的人数;
(2)通过计算,请补全条形统计图;
(3)如果这所学校有1500名学生,请估计该校最希望演示B项实验的学生有多少人
24.(本题8分)如图,在平行四边形ABCD中,E是对角线BD上的一点,过点C作,连接AE,BF.
(1)求证:;
(2)连接EF,若,在不添加其它辅助线的情况下,请直接写出图中与线段AB相等的线段.
25.(本题10分)我们度过了寒冬,迎来了充满希望的春天,同学们将走出教室进行适当的体育锻炼.九年一班想集体购买跳绳和毽子,第一次买20条跳绳和30个毽子共花了590元,第二次又买了10条跳绳和10个毽子共花了260元,请回答下面的两个问题:
(1)求跳绳和毽子的单价是多少元
(2)若九年二班也打算购买同样的跳绳和毽子共50个,且总花费不超过600元,问九年二班的跳绳最多买多少条
26.(本题10分)已知内接于,连接AO.
图1 图2 图3
(1)如图1,若于点M,求证:;
(2)如图2,点E为弧AB上一点,AD垂直BE于点D,交于点F,若AB平分,求证:;
(3)在(2)的条件下,如图3,,BG平分交于点G,连接AG,,若,求线段AB的长.
27.(本题10分)如图1,在平面直角坐标系中,O为坐标原点,抛物线与x轴负半轴交于点A,与x轴正半轴于点B,交y轴于点C,直线经过A,C两点.
图1 图2 图3
(1)求抛物线的解析式;
(2)如图2,点P为第一象限抛物线上一点,交y轴于点D,若设线段PD的长为d,点P的横坐标为t,求d与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,连接AD,点E为抛物线上第四象限上一点,,连接CE交x轴于点F,若,求点P的横坐标.
2023-2024学年度下学期九年级模拟考试题
数学试卷参考答案
一、1-5.ACCBC 6-10.ABADD
二、11. 12. 13. 14.13 15.
16. 17. 18. 19.3或 20.
三、21.解:原式
当
∴原式
22.(1)画图正确
(2)画图正确
23.解:(1)(人) 1'
答:此次调查中接受调查的人数是50人 1'
(2)最希望演示C实验的人数为 (人) 2' 补图略 .1'
(3) (人) 2'
答:估计该校最希望演示B项实验的学生有240人. 1'
24.解︰(1)∵四边形ABCD是平行四边形∴,∴. 1'
∵,∴,∴ 1'
∵,∴ 1'
∴ 1'
(2)AE、BF、EF、CD(每个1,共4分)
25.2 (1)解:设跳绳的单价为x元,毽子的单价为y元.
根据题意得: 2'
解得: 2'
答:跳绳的单价为19元,毽子的单价为7元. 1'
(2)设九年二班购买a条跳绳,则购买个毽子.
根据题意得: 2'
解得: 1'
∵a为正整数
∴a的最大值为20.
答:九年二班的跳绳最多买20条
26.(1)证明:连接OB,∴,∵,
∴,∴ 1'
∵,∴,
∴,∴ 1'
(2)连接AO,BO,∴,∵,
∴,∴,
∵,∴. 1'
∵,∴,
∴,∴ .1'
∴AB平分,
∴,∴ 1'
(3)连接OE,OB,延长AO交于点N,连接OC,CN
∵
∴,∴ 1'
∵BG平分,∴
连接OG交AC于点K
∵
∴,
∵
∴OG垂直平分AC,∵
∴. 1'
在和中
∴,解得 1'
∴
∴
过点E作于点T
∴ 1'
∵,∴,
∴. 1'
27.解:(1)∵直线经过A,C两点
∴当时,;当时,
∴ 1'
把代入得,解得
∴抛物线的解析式为 1'
(2)∵,∴
∴ 1'
过点Р作轴于点K,∴
∵,∴,
∴,∴ 2'
(3)过点D作交CA延长线于点M,于点N,
∴
∵四边形ADEC的内角和为,,
∴,∵,
∴ 1'
∵,∴, 1'
∴CD平分,∵,∴
∴,∴
设直线CF的解析式为,∴,解得
∴直线CF的解析式为. 1'
联立与组成方程组得
得,∴ 1'
设点,
过点E作于点Q,∴
∴
∴,解得 1'
∴
∴
解得
∴点P的横坐标是 1
同课章节目录
