内蒙古呼和浩特剑桥、世宙中学2023-2024学年下学期九年级寒假回测数学试卷(图片版无答案)
文档属性
| 名称 | 内蒙古呼和浩特剑桥、世宙中学2023-2024学年下学期九年级寒假回测数学试卷(图片版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-08 20:46:48 | ||
图片预览

文档简介
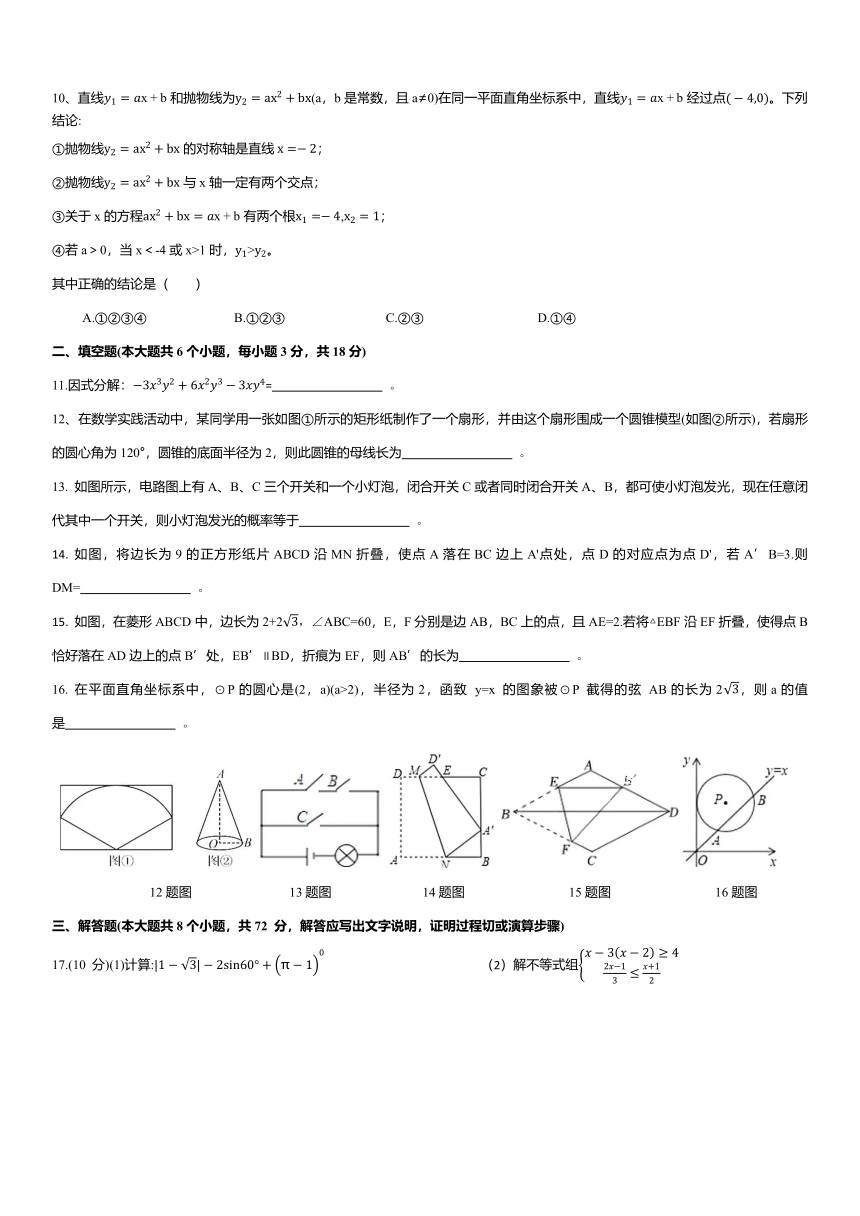
剑桥、世宙中学 2023-2024 学年第二学期初三年级寒假回测数学试卷
考试时间:120 分钟 试卷满分:120 分
一.选择题(本大题共 10 个小题,每小题 3 分,共 30 分。在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题
卡上将该项涂黑)
1.实数 5 的相反数是( )
A.5 B.-5 C.1 D. 1
5 5
2 关于 x 方程 2 + 3 + 3 = 0 的根的情况是( )
A.有两个不相等的实数根 B.无实根 C.有两个相等的实数根 D.只有一个实数根
3.如图,直线 m∥n,点 A 在直线 n 上,点 B 在直线 m 上,连接 AB,过点作 AC⊥AB,交直线 m 于点 C,若∠1=50°,则∠2 的度数为
( )
A.20° B.30° C.40° D.50°
(9 题图)
4.2023 年 10 月 18 日,第三届“一带一路“国际合作高峰论坛在北京举行,国家主席习近平在主旨演讲中声明:“本届高峰论坛期间举
行的企业家大会达成了 972 亿美元的项目合作协议”。将 972 亿美元用科学计数法表示成元,正确的是( )
A.9.72 × 102 B.9.72 × 109 C.9.72 × 1010 D.9.72 × 1011
5.若式子 1有意义,则 x 的取值范围是( )
2
A. > 1 B. > 1且 x ≠ 2 C. ≥ 1且 x ≠ 2 D.x ≠ 2
6.下列计算正确的是( )
A.3 2 2 2 = 1 B. + 2 = 2 + 2 C. 3 ÷ 6 = 1 4 59 D. = 9
7.三张图片除画面不同外无其他差别,将它们从中间剪断得到三张上部图片和三张下部图片,把三张上部图片放入一个布袋,把三张
下部图片放入另一个布袋,再分别从两个布袋中各随机摸取一张,则这两张小图片恰好合成一张完整图片的概率是( )
A.1 B.1 C.1 D.1
6 3 9 5
8.在同一平面直角坐标系中,一次函数 y = kx + k 与反比例函数 y = k的图象可能是( )
x
9、如图,在矩形 ABCD 中,对角线 4C 与 BD 相交于点 O,∠ABD=60°,AE⊥BD,垂足为点 E,F 是 OC 的中点,连接 EF,若 EF=2 3,
则矩形 ABCD 的周长是( )
A.16 3 B.8 3 + 4 C.4 3 + 8 D.8 3 +8
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
10、直线 1 = x + b 和抛物线为y2 = ax2 + bx(a,b 是常数,且 a≠0)在同一平面直角坐标系中,直线 1 = x + b 经过点( 4,0)。下列
结论:
①拋物线y 22 = ax + bx 的对称轴是直线 x = 2;
②抛物线y 22 = ax + bx 与 x 轴一定有两个交点;
③关于 x 的方程ax2 + bx = x + b 有两个根x1 = 4,x2 = 1;
④若 a>0,当 x<-4 或 x>1 时,y1>y2。
其中正确的结论是( )
A.①②③④ B.①②③ C.②③ D.①④
二、填空题(本大题共 6 个小题,每小题 3 分,共 18 分)
11.因式分解: 3 3 2 + 6 2 3 3 4= 。
12、在数学实践活动中,某同学用一张如图①所示的矩形纸制作了一个扇形,并由这个扇形围成一个圆锥模型(如图②所示),若扇形
的圆心角为 120°,圆锥的底面半径为 2,则此圆锥的母线长为 。
13. 如图所示,电路图上有 A、B、C 三个开关和一个小灯泡,闭合开关 C 或者同时闭合开关 A、B,都可使小灯泡发光,现在任意闭
代其中一个开关,则小灯泡发光的概率等于 。
14. 如图,将边长为 9 的正方形纸片 ABCD 沿 MN 折叠,使点 A 落在 BC 边上 A'点处,点 D 的对应点为点 D',若 A’B=3.则
DM= 。
15. 如图,在菱形 ABCD 中,边长为 2+2 3,∠ABC=60,E,F 分别是边 AB,BC 上的点,且 AE=2.若将△EBF 沿 EF 折叠,使得点 B
恰好落在 AD 边上的点 B’处,EB’∥BD,折痕为 EF,则 AB’的长为 。
16. 在平面直角坐标系中,⊙P 的圆心是(2,a)(a>2),半径为 2,函致 y=x 的图象被⊙P 截得的弦 AB 的长为 2 3,则 a 的值
是 。
12 题图 13 题图 14 题图 15 题图 16 题图
三、解答题(本大题共 8 个小题,共 72 分,解答应写出文字说明,证明过程切或演算步骤)
0 3 2 ≥ 4
17.(10 分)(1)计算:|1 3| 2sin60° + π 1 (2)解不等式组 2 1 ≤ +1
3 2
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
18.(5 分)关于 x 的一元二次方程x2 (2k 3)x + k2 + 1 = 0 有两不相等的实数根 1, 2。求 k 的取值范围;
(12 分)为了了解学生掌握垃圾分类知识的情况,增强学生环保意识.某校举行了“垃圾分类,人人有责”的知识测试活动,现从该校七、
八年级中各随机抽取 20 名学生的测试成绩(满分 10 分,6 分及 6 分以上为及格)进行整理、描述和分析,下面给出了部分信
七年级 20 名学生的测试成绩为:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、8 分及以上人数所占百分比如下表所示:根据以上信息,解答下列问题
年级 平均数 众数 中位数 8 分及以上人数所占百分比
七年级 7.5 a 7 45%
八年级 7.5 8 b c
(1)在上述表格中:a= ,b= ,c= ;
(2)根据上述数据,你认为该校七、八年级中哪个年级的学生掌握垃圾分类知识的情况较好 请说明理由(写出一条理由即可);
(3)该校德育处从八年级测试成绩前四名甲、乙、丙、丁学生中随机抽取 2 名学生参加全市现场垃圾分类知识竞赛,请用列表法或
面树状图法求出必有甲同学参加比赛的概率。
20. (7 分)如图,四边形 ABCD 中,对角线 AC、BD 相交于点 O,O 为 AC、BD 中点,AB=10,AC=16,BD=12
(1) 四边形 ABCD 是什么特殊的四近形 请证明;
(2) 点 P 在 AO 上,点 Q 在 DO 上,且 AP=OQ.若 PQ=BQ,求 AP 的长。
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
21.(7 分)如图,在平面直角坐标系中,点 O 为坐标原点,长方形 OABC 的边 OA、OC 分别在 x 轴、y 上,点 B 坐标为(2,3),双曲线
y = k 1(x>0)的图象经过线段 BC 的中点 D.
x
(1)求双曲线的解析式;
(2)若点 P(x,y)在反比例函数的图像上运动(不与点 D 重合),过 P 作 PQ⊥y 轴于点 Q,记△CPQ 的面积为 S,求 S 关于 x 的解
析式,并写出 x 的取值范围。
22、(9 分)某水果批发商销售每箱进价为 40 元的柑橘,物价部门规定每箱售价不得高于 55 元;市场调查发现,若每箱以 45 元的价格销
售,平均每天销构 105 箱;每箱以 50 元的价格销售,平均每天销售 90 箱、假定每天销售量 y(箱)与销售价 x(元/箱)之间满足一次函数关
系式。
(1)求平均每天销售量 y(箱)与销售价 x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润 W(元)与销售价 x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润 最大利润是多少
23、(10 分)如图,AB 是⊙O 直径,C 是弧 AB 的中点,⊙O 的切线 BD 交 AC 的延长线于点 D,E 是 OB 的中点,CE 的延长线交
切线 BD 于点 F,AF 交⊙O 于点 H,连接 BH。
(1)求证:AC=CD;
(2)若 OB=2,,求 BH 的长。
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
24. (12 分)已知抛物线 y = x2 + (3 m)x 2m+ 2
(1) 若抛物线经过坐标原点,求此时抛物线的解析式;
(2) 该抛物线的顶点随着 m 的变化而移动,当顶点移到最高处时,求该抛物线的顶点坐
已知点 E(-1,1),F(3,5),若该抛物线与线段 EF 只有一个交点,求该抛物线顶点横坐标的取值范围。
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
考试时间:120 分钟 试卷满分:120 分
一.选择题(本大题共 10 个小题,每小题 3 分,共 30 分。在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题
卡上将该项涂黑)
1.实数 5 的相反数是( )
A.5 B.-5 C.1 D. 1
5 5
2 关于 x 方程 2 + 3 + 3 = 0 的根的情况是( )
A.有两个不相等的实数根 B.无实根 C.有两个相等的实数根 D.只有一个实数根
3.如图,直线 m∥n,点 A 在直线 n 上,点 B 在直线 m 上,连接 AB,过点作 AC⊥AB,交直线 m 于点 C,若∠1=50°,则∠2 的度数为
( )
A.20° B.30° C.40° D.50°
(9 题图)
4.2023 年 10 月 18 日,第三届“一带一路“国际合作高峰论坛在北京举行,国家主席习近平在主旨演讲中声明:“本届高峰论坛期间举
行的企业家大会达成了 972 亿美元的项目合作协议”。将 972 亿美元用科学计数法表示成元,正确的是( )
A.9.72 × 102 B.9.72 × 109 C.9.72 × 1010 D.9.72 × 1011
5.若式子 1有意义,则 x 的取值范围是( )
2
A. > 1 B. > 1且 x ≠ 2 C. ≥ 1且 x ≠ 2 D.x ≠ 2
6.下列计算正确的是( )
A.3 2 2 2 = 1 B. + 2 = 2 + 2 C. 3 ÷ 6 = 1 4 59 D. = 9
7.三张图片除画面不同外无其他差别,将它们从中间剪断得到三张上部图片和三张下部图片,把三张上部图片放入一个布袋,把三张
下部图片放入另一个布袋,再分别从两个布袋中各随机摸取一张,则这两张小图片恰好合成一张完整图片的概率是( )
A.1 B.1 C.1 D.1
6 3 9 5
8.在同一平面直角坐标系中,一次函数 y = kx + k 与反比例函数 y = k的图象可能是( )
x
9、如图,在矩形 ABCD 中,对角线 4C 与 BD 相交于点 O,∠ABD=60°,AE⊥BD,垂足为点 E,F 是 OC 的中点,连接 EF,若 EF=2 3,
则矩形 ABCD 的周长是( )
A.16 3 B.8 3 + 4 C.4 3 + 8 D.8 3 +8
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
10、直线 1 = x + b 和抛物线为y2 = ax2 + bx(a,b 是常数,且 a≠0)在同一平面直角坐标系中,直线 1 = x + b 经过点( 4,0)。下列
结论:
①拋物线y 22 = ax + bx 的对称轴是直线 x = 2;
②抛物线y 22 = ax + bx 与 x 轴一定有两个交点;
③关于 x 的方程ax2 + bx = x + b 有两个根x1 = 4,x2 = 1;
④若 a>0,当 x<-4 或 x>1 时,y1>y2。
其中正确的结论是( )
A.①②③④ B.①②③ C.②③ D.①④
二、填空题(本大题共 6 个小题,每小题 3 分,共 18 分)
11.因式分解: 3 3 2 + 6 2 3 3 4= 。
12、在数学实践活动中,某同学用一张如图①所示的矩形纸制作了一个扇形,并由这个扇形围成一个圆锥模型(如图②所示),若扇形
的圆心角为 120°,圆锥的底面半径为 2,则此圆锥的母线长为 。
13. 如图所示,电路图上有 A、B、C 三个开关和一个小灯泡,闭合开关 C 或者同时闭合开关 A、B,都可使小灯泡发光,现在任意闭
代其中一个开关,则小灯泡发光的概率等于 。
14. 如图,将边长为 9 的正方形纸片 ABCD 沿 MN 折叠,使点 A 落在 BC 边上 A'点处,点 D 的对应点为点 D',若 A’B=3.则
DM= 。
15. 如图,在菱形 ABCD 中,边长为 2+2 3,∠ABC=60,E,F 分别是边 AB,BC 上的点,且 AE=2.若将△EBF 沿 EF 折叠,使得点 B
恰好落在 AD 边上的点 B’处,EB’∥BD,折痕为 EF,则 AB’的长为 。
16. 在平面直角坐标系中,⊙P 的圆心是(2,a)(a>2),半径为 2,函致 y=x 的图象被⊙P 截得的弦 AB 的长为 2 3,则 a 的值
是 。
12 题图 13 题图 14 题图 15 题图 16 题图
三、解答题(本大题共 8 个小题,共 72 分,解答应写出文字说明,证明过程切或演算步骤)
0 3 2 ≥ 4
17.(10 分)(1)计算:|1 3| 2sin60° + π 1 (2)解不等式组 2 1 ≤ +1
3 2
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
18.(5 分)关于 x 的一元二次方程x2 (2k 3)x + k2 + 1 = 0 有两不相等的实数根 1, 2。求 k 的取值范围;
(12 分)为了了解学生掌握垃圾分类知识的情况,增强学生环保意识.某校举行了“垃圾分类,人人有责”的知识测试活动,现从该校七、
八年级中各随机抽取 20 名学生的测试成绩(满分 10 分,6 分及 6 分以上为及格)进行整理、描述和分析,下面给出了部分信
七年级 20 名学生的测试成绩为:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、8 分及以上人数所占百分比如下表所示:根据以上信息,解答下列问题
年级 平均数 众数 中位数 8 分及以上人数所占百分比
七年级 7.5 a 7 45%
八年级 7.5 8 b c
(1)在上述表格中:a= ,b= ,c= ;
(2)根据上述数据,你认为该校七、八年级中哪个年级的学生掌握垃圾分类知识的情况较好 请说明理由(写出一条理由即可);
(3)该校德育处从八年级测试成绩前四名甲、乙、丙、丁学生中随机抽取 2 名学生参加全市现场垃圾分类知识竞赛,请用列表法或
面树状图法求出必有甲同学参加比赛的概率。
20. (7 分)如图,四边形 ABCD 中,对角线 AC、BD 相交于点 O,O 为 AC、BD 中点,AB=10,AC=16,BD=12
(1) 四边形 ABCD 是什么特殊的四近形 请证明;
(2) 点 P 在 AO 上,点 Q 在 DO 上,且 AP=OQ.若 PQ=BQ,求 AP 的长。
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
21.(7 分)如图,在平面直角坐标系中,点 O 为坐标原点,长方形 OABC 的边 OA、OC 分别在 x 轴、y 上,点 B 坐标为(2,3),双曲线
y = k 1(x>0)的图象经过线段 BC 的中点 D.
x
(1)求双曲线的解析式;
(2)若点 P(x,y)在反比例函数的图像上运动(不与点 D 重合),过 P 作 PQ⊥y 轴于点 Q,记△CPQ 的面积为 S,求 S 关于 x 的解
析式,并写出 x 的取值范围。
22、(9 分)某水果批发商销售每箱进价为 40 元的柑橘,物价部门规定每箱售价不得高于 55 元;市场调查发现,若每箱以 45 元的价格销
售,平均每天销构 105 箱;每箱以 50 元的价格销售,平均每天销售 90 箱、假定每天销售量 y(箱)与销售价 x(元/箱)之间满足一次函数关
系式。
(1)求平均每天销售量 y(箱)与销售价 x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润 W(元)与销售价 x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润 最大利润是多少
23、(10 分)如图,AB 是⊙O 直径,C 是弧 AB 的中点,⊙O 的切线 BD 交 AC 的延长线于点 D,E 是 OB 的中点,CE 的延长线交
切线 BD 于点 F,AF 交⊙O 于点 H,连接 BH。
(1)求证:AC=CD;
(2)若 OB=2,,求 BH 的长。
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
24. (12 分)已知抛物线 y = x2 + (3 m)x 2m+ 2
(1) 若抛物线经过坐标原点,求此时抛物线的解析式;
(2) 该抛物线的顶点随着 m 的变化而移动,当顶点移到最高处时,求该抛物线的顶点坐
已知点 E(-1,1),F(3,5),若该抛物线与线段 EF 只有一个交点,求该抛物线顶点横坐标的取值范围。
{#{QQABIYgQgggIAABAAQgCQwkoCkEQkAACAIoGBFAEMAIBSQFABAA=}#}
同课章节目录
