数学人教A版(2019)选择性必修第三册7.1.1条件概率 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.1.1条件概率 课件(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 36.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 01:04:02 | ||
图片预览







文档简介
(共24张PPT)
第七章 随机变量及其分布
概率是随机事件发生可能性大小的度量.在必修课程的概率学习中,我们结合古典概型,研究了简单随机事件及其概率的计算方法,并讨论了概率的一些性质.本章将在此基础上,结合古典概型,研究随机事件的条件概率,建立概率的乘法公式和全概率公式,并用它们计算较复杂事件的概率.
为了利用数学工具,并以简洁、统一的形式研究随机试验的规律,本章我们还将把随机试验的结果数量化,引入随机变量的概念.对离散型随机变量,我们主要研究其分布列及数字特征,并对二项分布、超几何分布进行重点研究.对于连续型随机变量,我们只研究服从正态分布的情况.通过用随机变量描述和分析随机试验,解决一些简单的实际问题,进一步体会概率模型的作用及概率思想和方法的特点.
章首语
7.1.1 条件概率
样本空间:随机事件E的所有基本结果组成的集合为E的样本空间。
一般用符号Ω表示样本空间的元素称为样本点数。
温故知新:相关概念
古典概型:一个随机试验E,它的基本事件有限个,并且每个基本
事件出现的概率相等。把这类概率模型称为古典概型
(等可能概型)
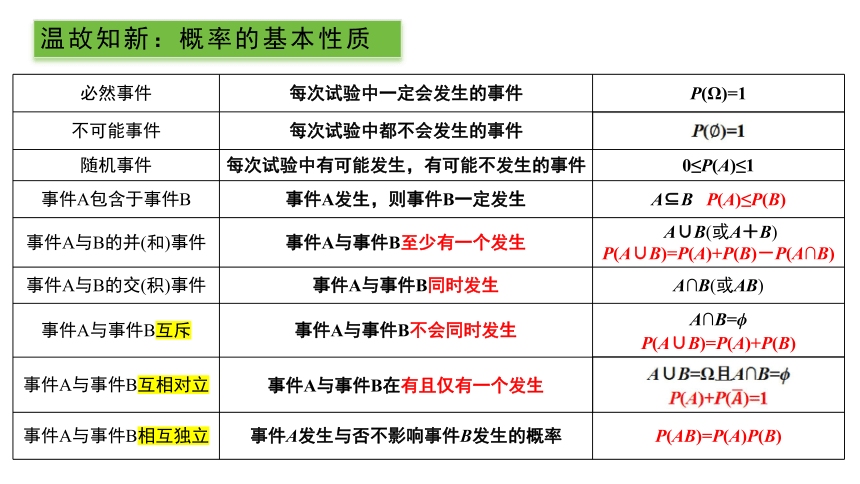
必然事件 每次试验中一定会发生的事件 P(Ω)=1
不可能事件 每次试验中都不会发生的事件 P()=1
随机事件 每次试验中有可能发生,有可能不发生的事件 0≤P(A)≤1
事件A包含于事件B 事件A发生,则事件B一定发生 A B P(A)≤P(B)
事件A与B的并(和)事件 事件A与事件B至少有一个发生 A∪B(或A+B)
P(A∪B)=P(A)+P(B)-P(A∩B)
事件A与B的交(积)事件 事件A与事件B同时发生 A∩B(或AB)
事件A与事件B互斥 事件A与事件B不会同时发生 A∩B=
P(A∪B)=P(A)+P(B)
事件A与事件B互相对立 事件A与事件B在有且仅有一个发生 A∪B=Ω且A∩B=
P(A)+P()=1
事件A与事件B相互独立 事件A发生与否不影响事件B发生的概率 P(AB)=P(A)P(B)
温故知新:概率的基本性质
在必修二《概率》一章的学习中,我们已经知道,
对于同一试验中的两个事件A与B,
当事件A与B相互独立时,事件A与B同时发生的概率有P(AB)=P(A)P(B).
当事件A与B不相互独立时,如何表示事件A与B同时发生(即积事件AB)的概率呢?
事件A发生会影响事件B发生的概率
事件A发生与否不会影响事件B发生的概率
问题提出
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如表所示.
在班级里随机选择一个做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
事件B:“选到男生”
n(B)=25
n(Ω)=45
事件A:“选到团员”
n(A)=30
此时相当于以A为样本空间来考虑事件B发生的概率;
在新的样本空间中,目标事件就是积事件AB,包含的样本点数n(AB)=16
“在事件A发生的条件下,事件B发生”的概率:
新课引入(课本p44)
问题2:假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭.
随机选择一个家庭,那么:
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
分析:用b表示男孩,g表示女孩,
则两个小孩的性别构成的样本空间Ω={bb, gg, bg, gb},且所有样本点是等可能的.
事件A:“选择的家庭中有女孩”,则A={ gg, bg, gb},
事件B:“选择的家庭中两个小孩都是女孩”,则B={bb}.
新课引入(课本p44)
“在事件A发生的条件下,事件B发生”的概率:
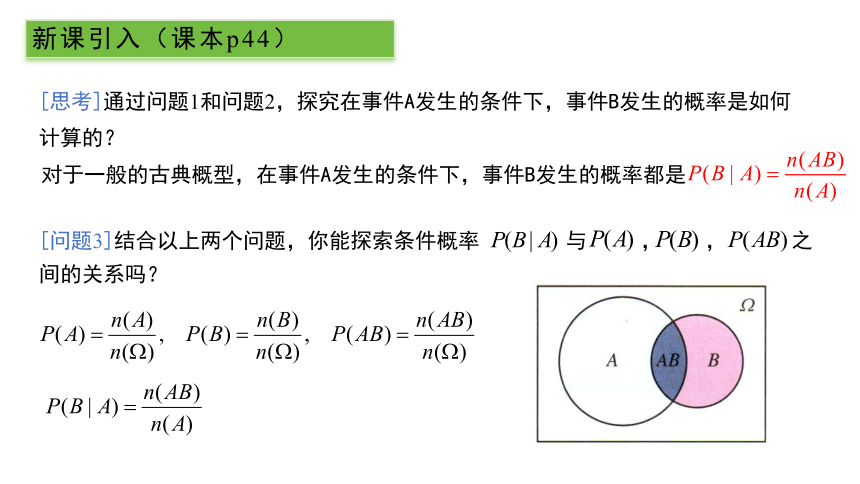
[思考]通过问题1和问题2,探究在事件A发生的条件下,事件B发生的概率是如何计算的?
对于一般的古典概型,在事件A发生的条件下,事件B发生的概率都是
新课引入(课本p44)
[问题3]结合以上两个问题,你能探索条件概率 与 , , 之间的关系吗?
[问题3]结合以上两个问题,你能探索条件概率 与 , , 之间的关系吗?
借助Venn图可知,若已知事件A发生,则A成为样本空间.
此时B发生的概率是AB包含样本点数与A包含样本点数的比值,即 .
因为
所以在事件A发生的条件下,事件B发生的概率可以通过 来计算
新课引入(课本p44)
一般地,设A,B为两个事件, 且P(A)>0, 称
为在事件A发生的条件下,事件B发生的条件概率.
一般把 P(B|A)读作 A 发生的条件下 B 发生的概率.
核心概念:条件概率
(1)若事件A,B互斥,则P(B|A)=0.( )
(2)若事件A B,则 ( )
设A, B为随机事件,且P(A)>0,则在事件A发生的条件下,事件B发生的条件概率:
注:若已知事件A发生,则A成为样本空间;此时,目标事件包含的样本点数与事件AB包含的样本点数相同.
条件概率的计算公式
(3)实际意义
√
√
(3)若B和C互斥,则P(B∪C|A)= P(B|A)+ P(C|A) ( )
√
√
探究:在问题1和问题2中,都有,为什么?
如果,那么事件与应满足什么条件?
答:从概率含义上分析:A发生的条件下B发生的概率等于B发生的概率,
说明A发生与否不影响B发生的概率,故事件A与B相互独立.
样本空间不同
条件概率的计算公式
从代数角度分析:
故事件相互独立。
由条件概率的定义,对任意两个事件A与B,
若P(A)>0,则P(AB)=P(A)P(B|A), 称此式为概率的乘法公式.
[追问]对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
例1. 在5道题中有3道代数题和2道几何题,
如果不放回地依次随机抽取2道题,求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率;
课本例题P46
析:记事件A:第1次抽到代数题;事件B:第2次抽到几何题;
则问题(1)求 ;问题(2)求
例1. 在5道题中有3道代数题和2道几何题,
如果不放回地依次随机抽取2道题,求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
课本例题P46
析:记事件A:第1次抽到代数题;事件B:第2次抽到几何题;
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取2道,试验的样本空间Ω包含20个等可能的样本点,即 ,
例1. 在5道题中有3道代数题和2道几何题,
如果不放回地依次随机抽取2道题,求:
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率;
析:记事件A:第1次抽到代数题;事件B:第2次抽到几何题;
课本例题P46
方法一
方法二
③第1次抽到代数题的条件下,还剩2道代数题和2道几何题
方法三
例1. 在5道题中有3道代数题和2道几何题,
如果不放回地依次随机抽取2道题,求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
课本例题P46
方法二
由(2)知 ,且
利用法公式可得
例2. 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张,他们中奖的概率与抽奖的次序有关吗?
目标:即研究3人中奖的概率是否相等.
析:记3张奖券为n1,n2,z,其中z表示中奖奖券;
记事件A,B,C分别表示甲、乙、丙中奖;
样本空间Ω={zn1n2 ,zn2n1,n1zn2 ,n2zn1,n1n2z, n2n1z}
A={zn1n2 ,zn2n1}
B={n1zn2 ,n2zn1}
C={n1n2z, n2n1z}
课本例题P47
例2. 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张,他们中奖的概率与抽奖的次序有关吗?
目标:即研究3人中奖的概率是否相等.
课本例题P47
课本例题P47
例3. 已银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
析:记事件Ai为“第i次按对密码”,
事件A为“不超过2次就按对”,
(2)记事件B为“最后一位为偶数”,
P48-1.设A B,且P(A)=0.3,P(B)=0.6. 根据事件包含关系的意义及条件概率的意义,直接写出P(B|A)和P(A|B)的值,再由条件概率公式进行验证.
A
B
练习巩固
分析:A B,A发生则B一定发生,所以P(AB)=P(B)
解:
[变式]已知某产品的合格率是,合格品中的一级品率是,则这种产品的一级品率是_____.
B
A
练习巩固
事件A:产品为合格品;
事件B:产品为一级品;
解:
分析:实际应用题用,要先把把题目条件、问题中的概率符号化
设A, B为随机事件,且P(A)>0,
则在事件A发生的条件下,事件B发生的条件概率记为
(1)求P(B|A):. ② ③直观意义
(3)性质:
①概率的乘法公式:
(2)求P(AB):
②A,B相互独立:
③
②若B和C互斥,则P(B∪C|A)= P(B|A)+ P(C|A)
③若和B互为对立事件,则P(|A)= 1-P(B|A)
课堂小结
谢谢
第七章 随机变量及其分布
概率是随机事件发生可能性大小的度量.在必修课程的概率学习中,我们结合古典概型,研究了简单随机事件及其概率的计算方法,并讨论了概率的一些性质.本章将在此基础上,结合古典概型,研究随机事件的条件概率,建立概率的乘法公式和全概率公式,并用它们计算较复杂事件的概率.
为了利用数学工具,并以简洁、统一的形式研究随机试验的规律,本章我们还将把随机试验的结果数量化,引入随机变量的概念.对离散型随机变量,我们主要研究其分布列及数字特征,并对二项分布、超几何分布进行重点研究.对于连续型随机变量,我们只研究服从正态分布的情况.通过用随机变量描述和分析随机试验,解决一些简单的实际问题,进一步体会概率模型的作用及概率思想和方法的特点.
章首语
7.1.1 条件概率
样本空间:随机事件E的所有基本结果组成的集合为E的样本空间。
一般用符号Ω表示样本空间的元素称为样本点数。
温故知新:相关概念
古典概型:一个随机试验E,它的基本事件有限个,并且每个基本
事件出现的概率相等。把这类概率模型称为古典概型
(等可能概型)
必然事件 每次试验中一定会发生的事件 P(Ω)=1
不可能事件 每次试验中都不会发生的事件 P()=1
随机事件 每次试验中有可能发生,有可能不发生的事件 0≤P(A)≤1
事件A包含于事件B 事件A发生,则事件B一定发生 A B P(A)≤P(B)
事件A与B的并(和)事件 事件A与事件B至少有一个发生 A∪B(或A+B)
P(A∪B)=P(A)+P(B)-P(A∩B)
事件A与B的交(积)事件 事件A与事件B同时发生 A∩B(或AB)
事件A与事件B互斥 事件A与事件B不会同时发生 A∩B=
P(A∪B)=P(A)+P(B)
事件A与事件B互相对立 事件A与事件B在有且仅有一个发生 A∪B=Ω且A∩B=
P(A)+P()=1
事件A与事件B相互独立 事件A发生与否不影响事件B发生的概率 P(AB)=P(A)P(B)
温故知新:概率的基本性质
在必修二《概率》一章的学习中,我们已经知道,
对于同一试验中的两个事件A与B,
当事件A与B相互独立时,事件A与B同时发生的概率有P(AB)=P(A)P(B).
当事件A与B不相互独立时,如何表示事件A与B同时发生(即积事件AB)的概率呢?
事件A发生会影响事件B发生的概率
事件A发生与否不会影响事件B发生的概率
问题提出
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
问题1:某个班级有45名学生,其中男生、女生的人数及团员的人数如表所示.
在班级里随机选择一个做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
事件B:“选到男生”
n(B)=25
n(Ω)=45
事件A:“选到团员”
n(A)=30
此时相当于以A为样本空间来考虑事件B发生的概率;
在新的样本空间中,目标事件就是积事件AB,包含的样本点数n(AB)=16
“在事件A发生的条件下,事件B发生”的概率:
新课引入(课本p44)
问题2:假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭.
随机选择一个家庭,那么:
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
分析:用b表示男孩,g表示女孩,
则两个小孩的性别构成的样本空间Ω={bb, gg, bg, gb},且所有样本点是等可能的.
事件A:“选择的家庭中有女孩”,则A={ gg, bg, gb},
事件B:“选择的家庭中两个小孩都是女孩”,则B={bb}.
新课引入(课本p44)
“在事件A发生的条件下,事件B发生”的概率:
[思考]通过问题1和问题2,探究在事件A发生的条件下,事件B发生的概率是如何计算的?
对于一般的古典概型,在事件A发生的条件下,事件B发生的概率都是
新课引入(课本p44)
[问题3]结合以上两个问题,你能探索条件概率 与 , , 之间的关系吗?
[问题3]结合以上两个问题,你能探索条件概率 与 , , 之间的关系吗?
借助Venn图可知,若已知事件A发生,则A成为样本空间.
此时B发生的概率是AB包含样本点数与A包含样本点数的比值,即 .
因为
所以在事件A发生的条件下,事件B发生的概率可以通过 来计算
新课引入(课本p44)
一般地,设A,B为两个事件, 且P(A)>0, 称
为在事件A发生的条件下,事件B发生的条件概率.
一般把 P(B|A)读作 A 发生的条件下 B 发生的概率.
核心概念:条件概率
(1)若事件A,B互斥,则P(B|A)=0.( )
(2)若事件A B,则 ( )
设A, B为随机事件,且P(A)>0,则在事件A发生的条件下,事件B发生的条件概率:
注:若已知事件A发生,则A成为样本空间;此时,目标事件包含的样本点数与事件AB包含的样本点数相同.
条件概率的计算公式
(3)实际意义
√
√
(3)若B和C互斥,则P(B∪C|A)= P(B|A)+ P(C|A) ( )
√
√
探究:在问题1和问题2中,都有,为什么?
如果,那么事件与应满足什么条件?
答:从概率含义上分析:A发生的条件下B发生的概率等于B发生的概率,
说明A发生与否不影响B发生的概率,故事件A与B相互独立.
样本空间不同
条件概率的计算公式
从代数角度分析:
故事件相互独立。
由条件概率的定义,对任意两个事件A与B,
若P(A)>0,则P(AB)=P(A)P(B|A), 称此式为概率的乘法公式.
[追问]对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
例1. 在5道题中有3道代数题和2道几何题,
如果不放回地依次随机抽取2道题,求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率;
课本例题P46
析:记事件A:第1次抽到代数题;事件B:第2次抽到几何题;
则问题(1)求 ;问题(2)求
例1. 在5道题中有3道代数题和2道几何题,
如果不放回地依次随机抽取2道题,求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
课本例题P46
析:记事件A:第1次抽到代数题;事件B:第2次抽到几何题;
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取2道,试验的样本空间Ω包含20个等可能的样本点,即 ,
例1. 在5道题中有3道代数题和2道几何题,
如果不放回地依次随机抽取2道题,求:
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率;
析:记事件A:第1次抽到代数题;事件B:第2次抽到几何题;
课本例题P46
方法一
方法二
③第1次抽到代数题的条件下,还剩2道代数题和2道几何题
方法三
例1. 在5道题中有3道代数题和2道几何题,
如果不放回地依次随机抽取2道题,求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
课本例题P46
方法二
由(2)知 ,且
利用法公式可得
例2. 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张,他们中奖的概率与抽奖的次序有关吗?
目标:即研究3人中奖的概率是否相等.
析:记3张奖券为n1,n2,z,其中z表示中奖奖券;
记事件A,B,C分别表示甲、乙、丙中奖;
样本空间Ω={zn1n2 ,zn2n1,n1zn2 ,n2zn1,n1n2z, n2n1z}
A={zn1n2 ,zn2n1}
B={n1zn2 ,n2zn1}
C={n1n2z, n2n1z}
课本例题P47
例2. 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张,他们中奖的概率与抽奖的次序有关吗?
目标:即研究3人中奖的概率是否相等.
课本例题P47
课本例题P47
例3. 已银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
析:记事件Ai为“第i次按对密码”,
事件A为“不超过2次就按对”,
(2)记事件B为“最后一位为偶数”,
P48-1.设A B,且P(A)=0.3,P(B)=0.6. 根据事件包含关系的意义及条件概率的意义,直接写出P(B|A)和P(A|B)的值,再由条件概率公式进行验证.
A
B
练习巩固
分析:A B,A发生则B一定发生,所以P(AB)=P(B)
解:
[变式]已知某产品的合格率是,合格品中的一级品率是,则这种产品的一级品率是_____.
B
A
练习巩固
事件A:产品为合格品;
事件B:产品为一级品;
解:
分析:实际应用题用,要先把把题目条件、问题中的概率符号化
设A, B为随机事件,且P(A)>0,
则在事件A发生的条件下,事件B发生的条件概率记为
(1)求P(B|A):. ② ③直观意义
(3)性质:
①概率的乘法公式:
(2)求P(AB):
②A,B相互独立:
③
②若B和C互斥,则P(B∪C|A)= P(B|A)+ P(C|A)
③若和B互为对立事件,则P(|A)= 1-P(B|A)
课堂小结
谢谢
