物理人教版(2019)必修第二册5.2专题2:绳关联模型和杆关联模型(共22张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册5.2专题2:绳关联模型和杆关联模型(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-09 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
绳关联模型和杆关联模型
1.理解为什么绳杆模型中速度是关联的:
两物体通过不可伸长(高中阶段研究的绳都是不可伸长的,杆都是不可伸长且不可压缩的,即绳或杆的长度不会改变)的轻绳(杆)相连,当两物体都发生运动,其速度通常是不一样的,但两个物体沿绳或杆方向的速度大小相等,我们称之为速度关联。
(
2.找出物体的合速度与分速度方向
认清哪个是合速度:物体的实际速度一定是合速度
认清哪个是分速度.:分解时两个分速度方向应取沿绳(杆)方向和垂直绳(杆)方向
3.列等量关系式
沿绳(或杆)方向的速度相等
如图,汽车甲用绳以速度v1拉着汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动
(1)在相等的时间内,甲和乙运动的位
移相等吗?
不相等.甲的位移x甲大于车的位移x乙
(2)小车甲和小车乙某一时刻的速度大小相等吗?如果不相等,哪个速度大?
不相等,相等时间内甲的位移x甲大于车的位移x乙.
甲的速度大于乙的速度.
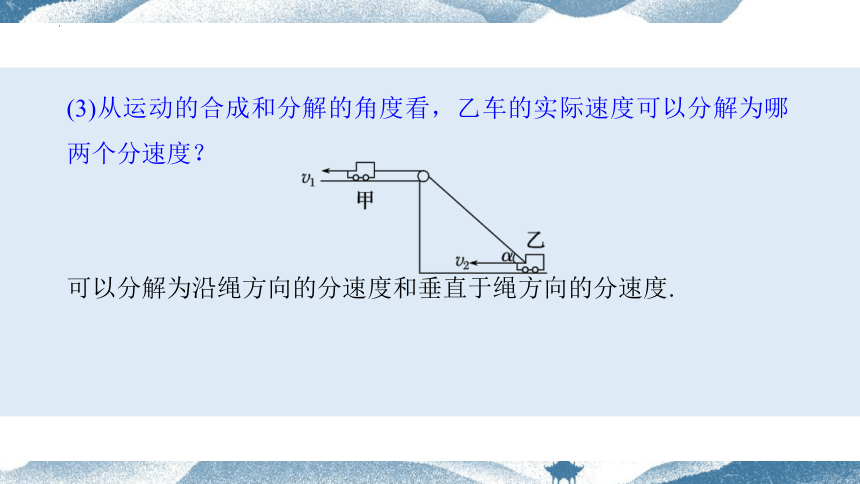
(3)从运动的合成和分解的角度看,乙车的实际速度可以分解为哪两个分速度?
可以分解为沿绳方向的分速度和垂直于绳方向的分速度.
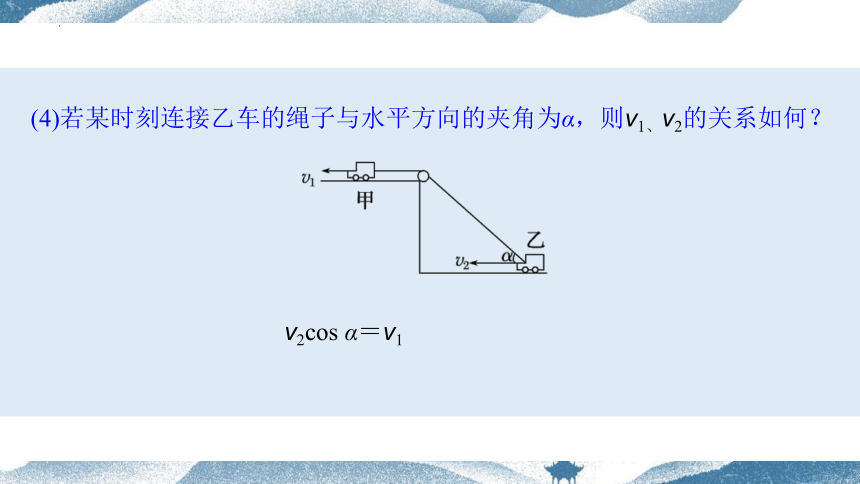
(4)若某时刻连接乙车的绳子与水平方向的夹角为α,则v1、v2的关系如何?
v2cos α=v1
绳模型举例:
(1)实际速度:绳的速度v,小木块的速度
(2)连接物:绳(沿绳方向速度一样)
(3)分解速度:沿绳v∥
(4)结论:v=v∥=v物cos θ
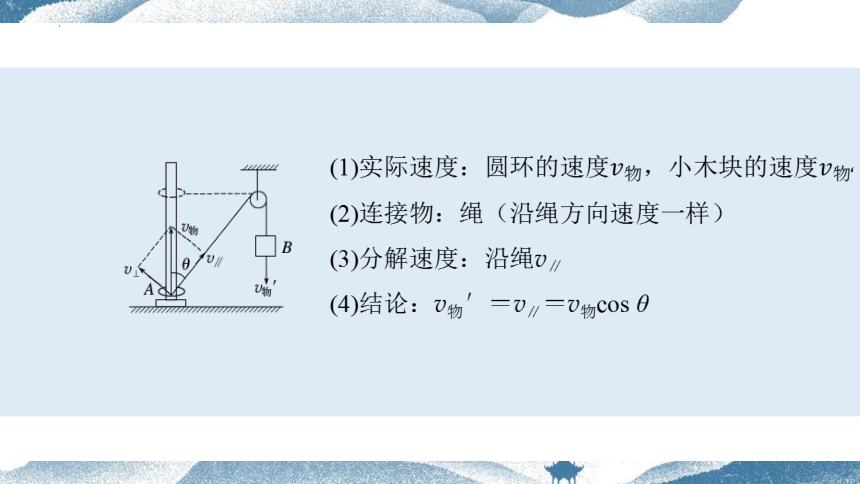
(1)实际速度:圆环的速度,小木块的速度
(2)连接物:绳(沿绳方向速度一样)
(3)分解速度:沿绳v∥
(4)结论:v物′=v∥=v物cos θ
(1)实际速度:小车B的速度,小车A的速度
(2)连接物:绳(沿绳方向速度一样)
(3)分解速度:沿绳v∥、v∥′
(4)结论:v物cos α=v物′cos β
杆模型举例:
(1)实际速度:杆上端的速度,下端的速度
(2)连接物:杆(沿杆方向速度一样)
(3)分解沿杆速度:沿绳v∥、v∥′
(4)结论:v物cos θ=v物′cos α
1.如图所示,有两条位于同一竖直平面内的水平轨道,轨道上有两个物体A和B,它们通过一根绕过光滑轻质定滑轮O的不可伸长的轻绳相连接,物体A以速率vA=10 m/s匀速运动,在绳与轨道成30°角时,物体B的速度大小vB为
√
例题:
物体B的速度可分解为如图所示的两个分速度,由图可知vB∥=vBcos 30°,由于绳不可伸长,有vB∥=vA,故vA=vBcos 30°,所以vB= ,故选D.
2.如图所示,一轻杆两端分别固定质量为mA和mB的小球A和B(A、B均可视为质点).将其放在一个光滑球形容器中从位置1开始下滑,当轻杆到达位置2时球A与球形容器球心等高,其速度大小为v1,已知此时轻杆与水平面成θ=30°角,球B的速度大小为v2,则
√
小球A与球形容器球心等高,速度v1方向竖直向下,速度分解如图所示,有v11=v1sin 30°= v1,由几何知识可知小球B此时速度方向与杆成α=60°角,因此v21=v2cos 60°= v2,两球沿杆方向的速度相等,即v21=v11,解得v2=v1,故选C.
课堂练习:
1.如图所示,在不计滑轮摩擦和绳子质量的条件下,当汽车匀速向左运动时,物体M的受力和运动情况是
A.绳的拉力等于M的重力
B.绳的拉力大于M的重力
C.物体M向上做匀速运动
D.物体M向上做匀加速运动
√
汽车匀速向左运动,其速度可分解为沿绳子方向和垂直于绳子方向,沿绳子方向的分速度v′=vcos θ,汽车在匀速向左运动的过程中,绳子与水平方向的夹角θ减小,所以v′增大,即物体M向上做加速运动,又因为v′变化不均匀,所以不是匀加速运
动,选项C、D错误;
由于物体M向上做加速运动,由F-mg=ma可知,
绳子的拉力大于M的重力,选项A错误,B正确.
2.如图所示,一个长直轻杆两端分别固定小球A和B,竖直放置,两球质量均为m,两球半径忽略不计,杆的长度为L.由于微小的扰动,A球沿竖直光滑槽向下运动,B球沿水平光滑槽向右运动,当杆与竖直方向的夹角为θ时(图中未标出),关于两球速度vA和vB的关系,下列说法正确的是
A.若θ=30°,则A、B两球的速度大小相等
B.若θ=60°,则A、B两球的速度大小相等
C.vA=vBtan θ
D.vA=vBsin θ
√
当杆与竖直方向的夹角为θ时,根据运动的分解可知(如图所示),沿杆方向两分速度大小相等,vAcos θ=vBsin θ,即vA=vBtan θ.当θ=45°时,vA=vB,故选C.
3.如图所示,水平固定的光滑细长杆上套有一物块Q,跨过悬挂于O点的轻小光滑圆环的细线一端连接Q,另一端悬挂一物块P.设细线的左边部分与水平方向的夹角为θ,初始时θ很小,现将P、Q由静止同时释放,关于P、Q以后的运动,下列说法正确的是
A.当θ=90°时,Q的速度为零
B.当θ=90°时,P的速度为零
C.当θ=60°时,P、Q的速度大小之比是 ∶2
D.在θ向90°增大的过程中,P一直处于失重状态
√
当θ=90°时,即为Q到达O点正下方时,此时Q
的速度最大,P的速度最小为零,故A错误,B
正确;
由题可知,P、Q用同一根细线连接,则Q沿细线
方向的速度与P的速度相等,则当θ=60°时,vQcos 60°=vP,解得vP∶vQ=1∶2,故C错误;
P从开始运动到到达最低点的过程中,先向下做加速运动,加速度向下,处于失重状态,然后又减速向下运动,加速度向上,处于超重状态,故D错误.
下课啦
绳关联模型和杆关联模型
1.理解为什么绳杆模型中速度是关联的:
两物体通过不可伸长(高中阶段研究的绳都是不可伸长的,杆都是不可伸长且不可压缩的,即绳或杆的长度不会改变)的轻绳(杆)相连,当两物体都发生运动,其速度通常是不一样的,但两个物体沿绳或杆方向的速度大小相等,我们称之为速度关联。
(
2.找出物体的合速度与分速度方向
认清哪个是合速度:物体的实际速度一定是合速度
认清哪个是分速度.:分解时两个分速度方向应取沿绳(杆)方向和垂直绳(杆)方向
3.列等量关系式
沿绳(或杆)方向的速度相等
如图,汽车甲用绳以速度v1拉着汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动
(1)在相等的时间内,甲和乙运动的位
移相等吗?
不相等.甲的位移x甲大于车的位移x乙
(2)小车甲和小车乙某一时刻的速度大小相等吗?如果不相等,哪个速度大?
不相等,相等时间内甲的位移x甲大于车的位移x乙.
甲的速度大于乙的速度.
(3)从运动的合成和分解的角度看,乙车的实际速度可以分解为哪两个分速度?
可以分解为沿绳方向的分速度和垂直于绳方向的分速度.
(4)若某时刻连接乙车的绳子与水平方向的夹角为α,则v1、v2的关系如何?
v2cos α=v1
绳模型举例:
(1)实际速度:绳的速度v,小木块的速度
(2)连接物:绳(沿绳方向速度一样)
(3)分解速度:沿绳v∥
(4)结论:v=v∥=v物cos θ
(1)实际速度:圆环的速度,小木块的速度
(2)连接物:绳(沿绳方向速度一样)
(3)分解速度:沿绳v∥
(4)结论:v物′=v∥=v物cos θ
(1)实际速度:小车B的速度,小车A的速度
(2)连接物:绳(沿绳方向速度一样)
(3)分解速度:沿绳v∥、v∥′
(4)结论:v物cos α=v物′cos β
杆模型举例:
(1)实际速度:杆上端的速度,下端的速度
(2)连接物:杆(沿杆方向速度一样)
(3)分解沿杆速度:沿绳v∥、v∥′
(4)结论:v物cos θ=v物′cos α
1.如图所示,有两条位于同一竖直平面内的水平轨道,轨道上有两个物体A和B,它们通过一根绕过光滑轻质定滑轮O的不可伸长的轻绳相连接,物体A以速率vA=10 m/s匀速运动,在绳与轨道成30°角时,物体B的速度大小vB为
√
例题:
物体B的速度可分解为如图所示的两个分速度,由图可知vB∥=vBcos 30°,由于绳不可伸长,有vB∥=vA,故vA=vBcos 30°,所以vB= ,故选D.
2.如图所示,一轻杆两端分别固定质量为mA和mB的小球A和B(A、B均可视为质点).将其放在一个光滑球形容器中从位置1开始下滑,当轻杆到达位置2时球A与球形容器球心等高,其速度大小为v1,已知此时轻杆与水平面成θ=30°角,球B的速度大小为v2,则
√
小球A与球形容器球心等高,速度v1方向竖直向下,速度分解如图所示,有v11=v1sin 30°= v1,由几何知识可知小球B此时速度方向与杆成α=60°角,因此v21=v2cos 60°= v2,两球沿杆方向的速度相等,即v21=v11,解得v2=v1,故选C.
课堂练习:
1.如图所示,在不计滑轮摩擦和绳子质量的条件下,当汽车匀速向左运动时,物体M的受力和运动情况是
A.绳的拉力等于M的重力
B.绳的拉力大于M的重力
C.物体M向上做匀速运动
D.物体M向上做匀加速运动
√
汽车匀速向左运动,其速度可分解为沿绳子方向和垂直于绳子方向,沿绳子方向的分速度v′=vcos θ,汽车在匀速向左运动的过程中,绳子与水平方向的夹角θ减小,所以v′增大,即物体M向上做加速运动,又因为v′变化不均匀,所以不是匀加速运
动,选项C、D错误;
由于物体M向上做加速运动,由F-mg=ma可知,
绳子的拉力大于M的重力,选项A错误,B正确.
2.如图所示,一个长直轻杆两端分别固定小球A和B,竖直放置,两球质量均为m,两球半径忽略不计,杆的长度为L.由于微小的扰动,A球沿竖直光滑槽向下运动,B球沿水平光滑槽向右运动,当杆与竖直方向的夹角为θ时(图中未标出),关于两球速度vA和vB的关系,下列说法正确的是
A.若θ=30°,则A、B两球的速度大小相等
B.若θ=60°,则A、B两球的速度大小相等
C.vA=vBtan θ
D.vA=vBsin θ
√
当杆与竖直方向的夹角为θ时,根据运动的分解可知(如图所示),沿杆方向两分速度大小相等,vAcos θ=vBsin θ,即vA=vBtan θ.当θ=45°时,vA=vB,故选C.
3.如图所示,水平固定的光滑细长杆上套有一物块Q,跨过悬挂于O点的轻小光滑圆环的细线一端连接Q,另一端悬挂一物块P.设细线的左边部分与水平方向的夹角为θ,初始时θ很小,现将P、Q由静止同时释放,关于P、Q以后的运动,下列说法正确的是
A.当θ=90°时,Q的速度为零
B.当θ=90°时,P的速度为零
C.当θ=60°时,P、Q的速度大小之比是 ∶2
D.在θ向90°增大的过程中,P一直处于失重状态
√
当θ=90°时,即为Q到达O点正下方时,此时Q
的速度最大,P的速度最小为零,故A错误,B
正确;
由题可知,P、Q用同一根细线连接,则Q沿细线
方向的速度与P的速度相等,则当θ=60°时,vQcos 60°=vP,解得vP∶vQ=1∶2,故C错误;
P从开始运动到到达最低点的过程中,先向下做加速运动,加速度向下,处于失重状态,然后又减速向下运动,加速度向上,处于超重状态,故D错误.
下课啦
